北师大版七下:3.2 用关系式表示的变量间关系 课件(21张)
文档属性
| 名称 | 北师大版七下:3.2 用关系式表示的变量间关系 课件(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 933.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览





文档简介
用关系式表示的变量间的关系
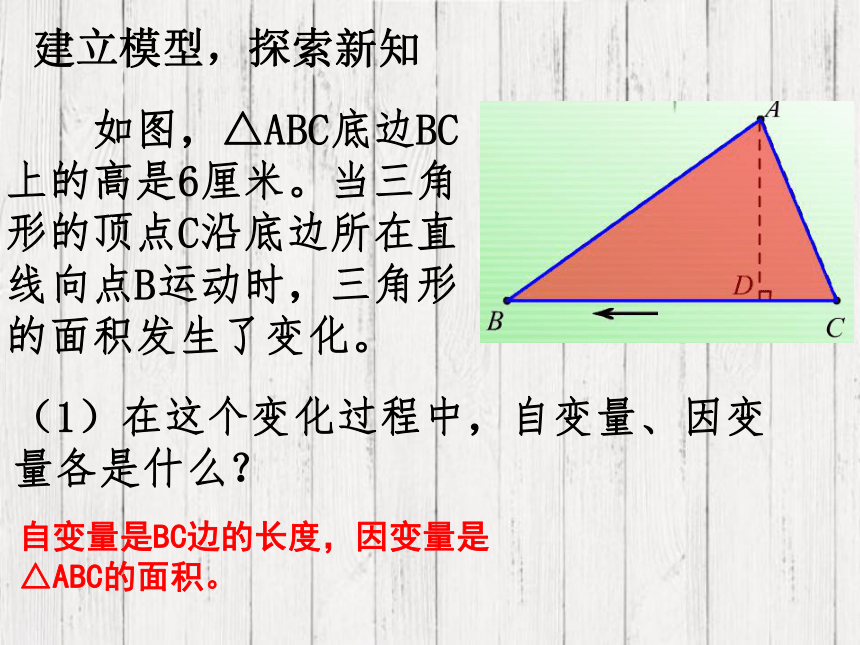
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化。
(1)在这个变化过程中,自变量、因变量各是什么?
建立模型,探索新知
自变量是BC边的长度,因变量是△ABC的面积。
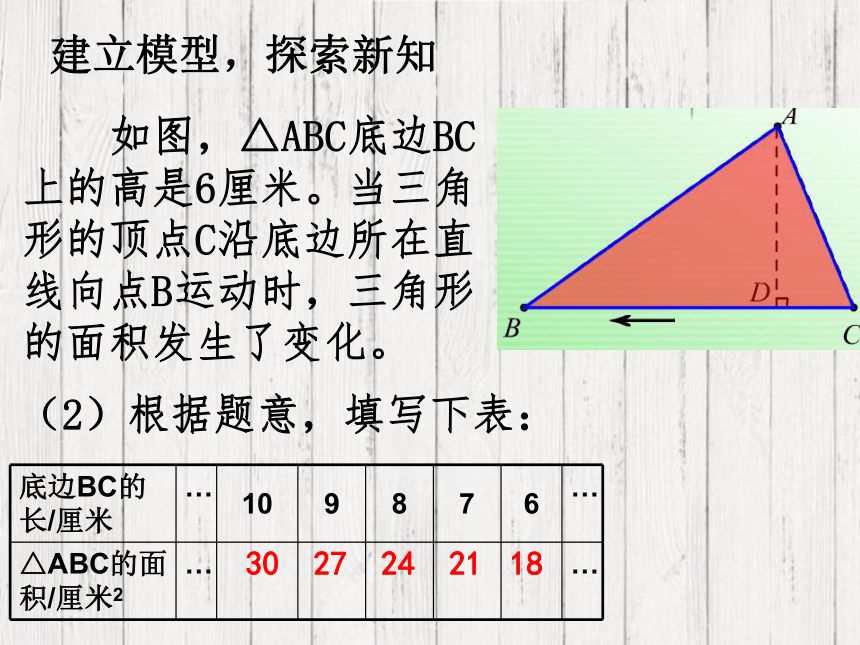
(2)根据题意,填写下表:
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化。
底边BC的长/厘米
…
10
9
8
7
6
…
△ABC的面积/厘米2
…
…
建立模型,探索新知
30
27
24
21
18
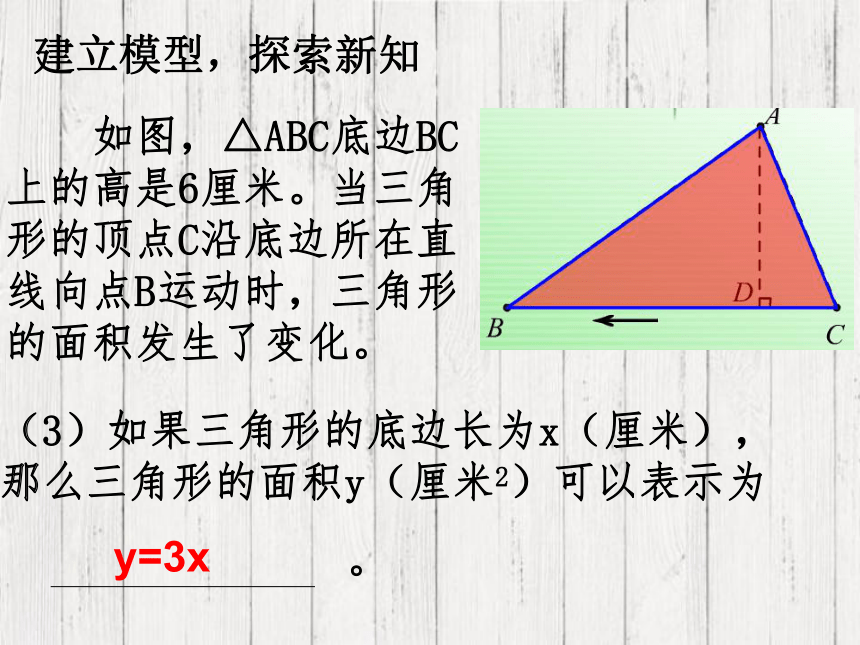
(3)如果三角形的底边长为x(厘米),那么三角形的面积y(厘米2)可以表示为
。
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化。
建立模型,探索新知
y=3x
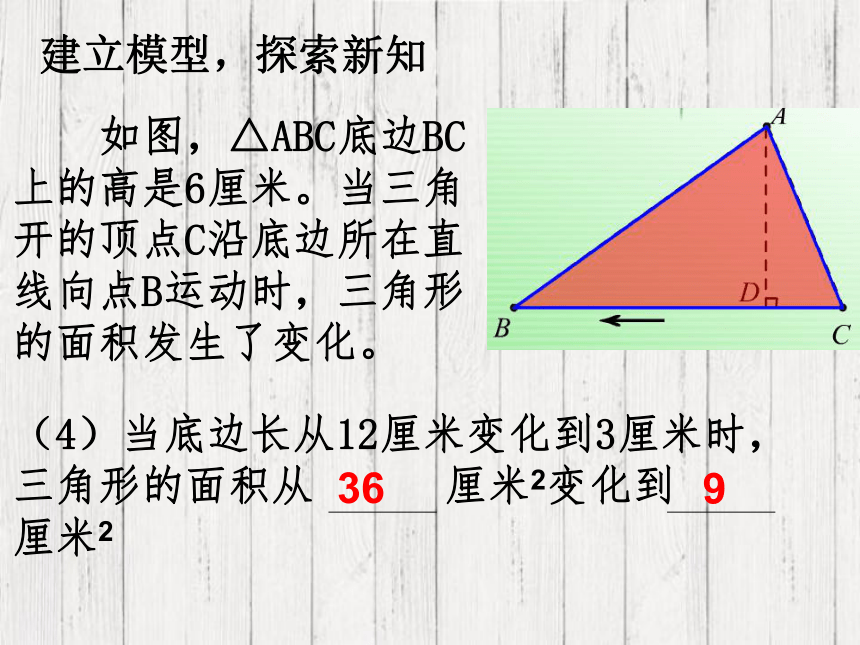
如图,△ABC底边BC上的高是6厘米。当三角开的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化。
(4)当底边长从12厘米变化到3厘米时,三角形的面积从 厘米2变化到 厘米2
建立模型,探索新知
36
9
注意:关系式是一个等式;通常把因变量写在等号的左边,含有自变量的代数式写在等号的右边。
关系式是我们比较变量之间关系的另一种方法。
利用关系式,如y=3x ,可以根据任何一个符合条件的自变量的值求出因变量的值。
做一做,应用新知
1、 如图,圆锥的底面半径是2厘米,当圆锥的高由小到大变化时,圆锥的体积也随之变化。
(1)在这个变化过程中,自变量、因变量各是什么?
自变量是圆锥的高,因变量是圆锥的体积。
做一做,应用新知
1、 如图,圆锥的底面半径是2厘米,当圆锥的高由小到大变化时,圆锥的体积也随之变化。
(2)如果圆锥的高为h(厘米),那么圆锥的体积V(厘米3)与h之间的关系式为 .
做一做,应用新知
1、 如图,圆锥的底面半径是2厘米,当圆锥的高由小到大变化时,圆锥的体积也随之变化。
(3)当高由1厘米变化到10厘米时,圆锥的体积由 厘米3变化到 厘米3
2、 如图,圆锥的高度是4厘米,当圆锥的的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
做一做,应用新知
(1)在这个变化过程中,自变量、因变量各是什么?
自变量是圆锥的底面半径,因变量是圆锥的体积。
2、 如图,圆锥的高度是4厘米,当圆锥的的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
做一做,应用新知
(2)如果圆锥底面半径为r(厘米),那么圆锥的体积V(厘米3)与r的关系式为______________
2、 如图,圆锥的高度是4厘米,当圆锥的的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
做一做,应用新知
(3)当底面半径由1厘米变化到10厘米时,圆锥的体积由 厘米3变化到 厘米3 。
小组活动,合作交流
素材:如图所示,梯形上底的长是x,下底的长是15,高是8。
请根据老师提供的素材,以小组为单位,设计一个变化过程,提出相关的问题,并进行解答。
A
B
C
D
E
A
B
C
D
E
3.如图所示,梯形上底的长是x,下底的长是15,高是8。
(1)梯形面积y与上底长x之间的关系式是什么?
小组活动,合作交流
y=4x+60
A
B
C
D
E
3.如图所示,梯形上底的长是x,下底的长是15,高是8。
(2)用表格表示当x从10变到14时(每次增加1),y的相应值;
小组活动,合作交流
上底x
面积y
10
11
12
13
14
100
104
108
112
116
y=4x+60
A
B
C
D
E
3.如图所示,梯形上底的长是x,下底的长是15,高是8。
(3)当x每增加1时,y如何变化?说说你的理由。
小组活动,合作交流
上底x
面积y
10
11
12
13
14
100
104
108
112
116
X每增加1,y增加4
y=4x+60
A
B
C
D
E
3.如图所示,梯形上底的长是x,下底的长是15,高是8。
(4)当x=0时,y等于什么?此时它表示的是什么?
小组活动,合作交流
当x=0时,y=60,此时它表示的是三角形的面积。
A
B
C
(D)
E
y=4x+60
如图:长方形的宽为8cm,长为x cm,周长为 y cm,
⑴、写出y与x之间的关系式;
⑵、当x=10cm时,y的值等于多少cm?
⑶、当y=40cm时,x的值等于多少cm?
8
x
练一练
1
2
3
4
感悟与反思
这节课你学到了什么?
本节课主要探索了图形中的变量关系
利用关系式表示变量之间的关系
能根据关系式求出相关的数值
读一读,知识拓展
(1)写出龙舟队在比赛时,距终点的距离S(米)与时间t(分钟)之间的关系式。
读一读,知识拓展
(2)当t的值分别是0,5,10,15,20时,计算相应的S值,并用表格表示所得的结果。
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化。
(1)在这个变化过程中,自变量、因变量各是什么?
建立模型,探索新知
自变量是BC边的长度,因变量是△ABC的面积。
(2)根据题意,填写下表:
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化。
底边BC的长/厘米
…
10
9
8
7
6
…
△ABC的面积/厘米2
…
…
建立模型,探索新知
30
27
24
21
18
(3)如果三角形的底边长为x(厘米),那么三角形的面积y(厘米2)可以表示为
。
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化。
建立模型,探索新知
y=3x
如图,△ABC底边BC上的高是6厘米。当三角开的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化。
(4)当底边长从12厘米变化到3厘米时,三角形的面积从 厘米2变化到 厘米2
建立模型,探索新知
36
9
注意:关系式是一个等式;通常把因变量写在等号的左边,含有自变量的代数式写在等号的右边。
关系式是我们比较变量之间关系的另一种方法。
利用关系式,如y=3x ,可以根据任何一个符合条件的自变量的值求出因变量的值。
做一做,应用新知
1、 如图,圆锥的底面半径是2厘米,当圆锥的高由小到大变化时,圆锥的体积也随之变化。
(1)在这个变化过程中,自变量、因变量各是什么?
自变量是圆锥的高,因变量是圆锥的体积。
做一做,应用新知
1、 如图,圆锥的底面半径是2厘米,当圆锥的高由小到大变化时,圆锥的体积也随之变化。
(2)如果圆锥的高为h(厘米),那么圆锥的体积V(厘米3)与h之间的关系式为 .
做一做,应用新知
1、 如图,圆锥的底面半径是2厘米,当圆锥的高由小到大变化时,圆锥的体积也随之变化。
(3)当高由1厘米变化到10厘米时,圆锥的体积由 厘米3变化到 厘米3
2、 如图,圆锥的高度是4厘米,当圆锥的的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
做一做,应用新知
(1)在这个变化过程中,自变量、因变量各是什么?
自变量是圆锥的底面半径,因变量是圆锥的体积。
2、 如图,圆锥的高度是4厘米,当圆锥的的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
做一做,应用新知
(2)如果圆锥底面半径为r(厘米),那么圆锥的体积V(厘米3)与r的关系式为______________
2、 如图,圆锥的高度是4厘米,当圆锥的的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
做一做,应用新知
(3)当底面半径由1厘米变化到10厘米时,圆锥的体积由 厘米3变化到 厘米3 。
小组活动,合作交流
素材:如图所示,梯形上底的长是x,下底的长是15,高是8。
请根据老师提供的素材,以小组为单位,设计一个变化过程,提出相关的问题,并进行解答。
A
B
C
D
E
A
B
C
D
E
3.如图所示,梯形上底的长是x,下底的长是15,高是8。
(1)梯形面积y与上底长x之间的关系式是什么?
小组活动,合作交流
y=4x+60
A
B
C
D
E
3.如图所示,梯形上底的长是x,下底的长是15,高是8。
(2)用表格表示当x从10变到14时(每次增加1),y的相应值;
小组活动,合作交流
上底x
面积y
10
11
12
13
14
100
104
108
112
116
y=4x+60
A
B
C
D
E
3.如图所示,梯形上底的长是x,下底的长是15,高是8。
(3)当x每增加1时,y如何变化?说说你的理由。
小组活动,合作交流
上底x
面积y
10
11
12
13
14
100
104
108
112
116
X每增加1,y增加4
y=4x+60
A
B
C
D
E
3.如图所示,梯形上底的长是x,下底的长是15,高是8。
(4)当x=0时,y等于什么?此时它表示的是什么?
小组活动,合作交流
当x=0时,y=60,此时它表示的是三角形的面积。
A
B
C
(D)
E
y=4x+60
如图:长方形的宽为8cm,长为x cm,周长为 y cm,
⑴、写出y与x之间的关系式;
⑵、当x=10cm时,y的值等于多少cm?
⑶、当y=40cm时,x的值等于多少cm?
8
x
练一练
1
2
3
4
感悟与反思
这节课你学到了什么?
本节课主要探索了图形中的变量关系
利用关系式表示变量之间的关系
能根据关系式求出相关的数值
读一读,知识拓展
(1)写出龙舟队在比赛时,距终点的距离S(米)与时间t(分钟)之间的关系式。
读一读,知识拓展
(2)当t的值分别是0,5,10,15,20时,计算相应的S值,并用表格表示所得的结果。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
