北师大版七年级下册2.3.2平行线的性质 课件(13张)
文档属性
| 名称 | 北师大版七年级下册2.3.2平行线的性质 课件(13张) |  | |
| 格式 | pptx | ||
| 文件大小 | 612.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 17:58:44 | ||
图片预览


文档简介
2.3.2 平行线的性质
平行线性质与判定的综合运用
第二章 相交线与平行线
北师版七年级下册数学
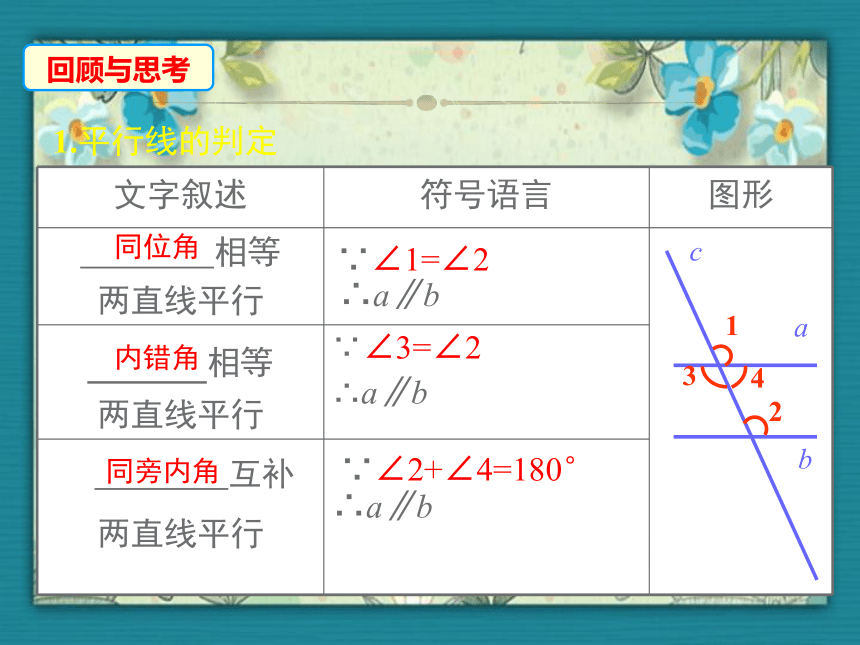
文字叙述
符号语言
图形
相等
两直线平行
∴a∥b
相等
两直线平行
∵
∴a∥b
互补
两直线平行
∴a∥b
同位角
内错角
同旁内角
∵∠1=∠2
∠3=∠2
∵∠2+∠4=180°
a
b
c
1
2
3
4
1.平行线的判定
回顾与思考
方法4:如图1,若a∥b,b∥c,则a∥c.
( )
方法5:如图2,若a⊥b,a⊥c,则b∥c.
( )
在同一平面内,平行于同一条直线的两条直线平行
在同一平面内,垂直于同一条直线的两条直线平行
2.平行线的其它判定方法
a
b
c
图1
a
b
c
图2
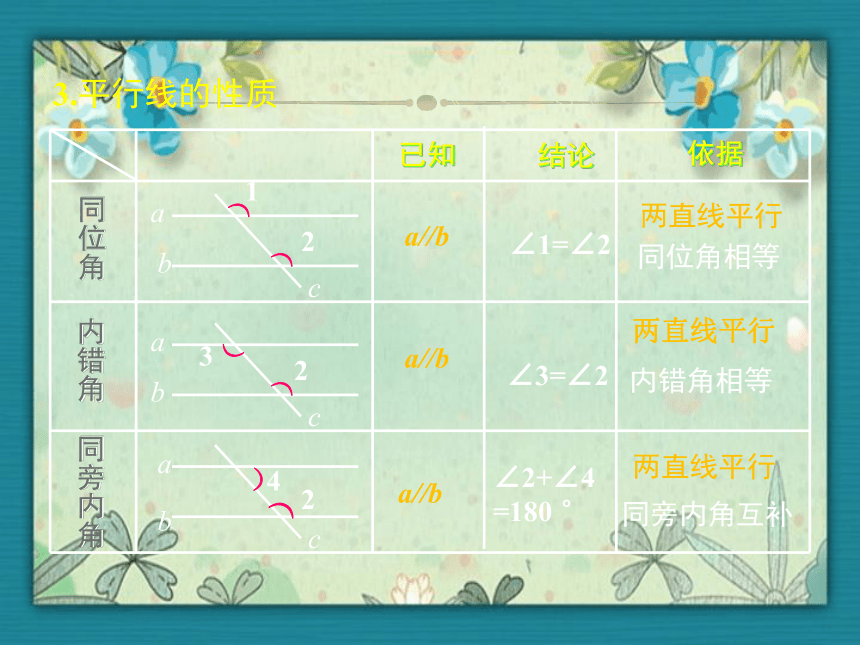
已知
结论
依据
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
3.平行线的性质
∠1=∠2
∠3=∠2
∠2+∠4
=180 °
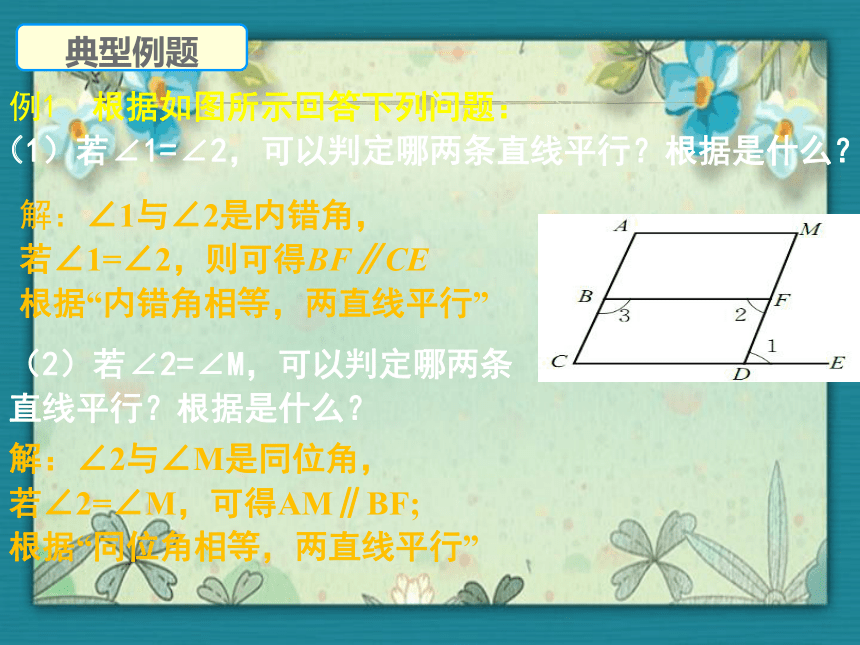
例1 根据如图所示回答下列问题:
(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
典型例题
解:∠1与∠2是内错角,
若∠1=∠2,则可得BF∥CE
根据“内错角相等,两直线平行”
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
解:∠2与∠M是同位角,
若∠2=∠M,可得AM∥BF;
根据“同位角相等,两直线平行”
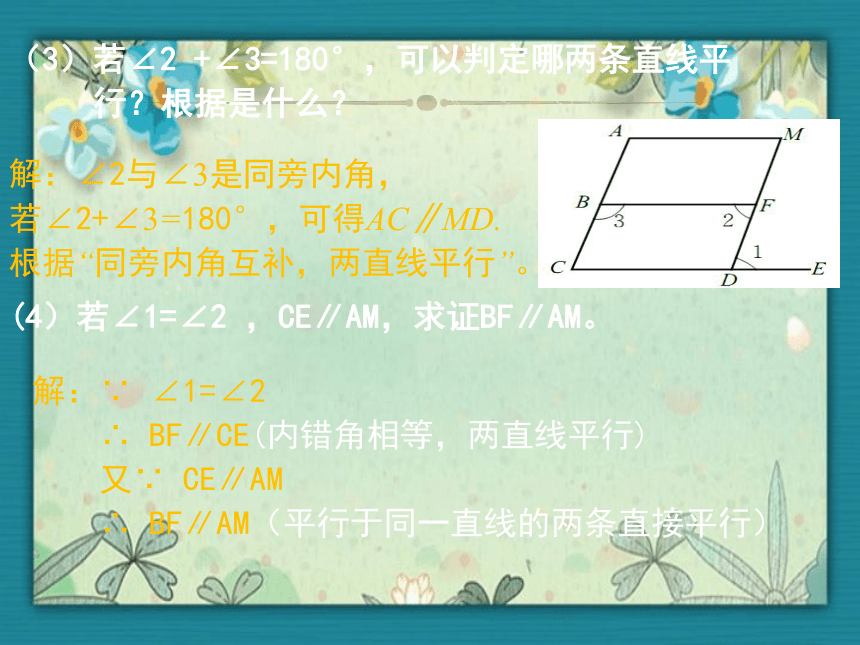
(3)若∠2 +∠3=180°,可以判定哪两条直线平
行?根据是什么?
解:∠2与∠3是同旁内角,
若∠2+∠3=180°,可得AC∥MD.
根据“同旁内角互补,两直线平行”。
(4)若∠1=∠2 ,CE∥AM,求证BF∥AM。
解:∵ ∠1=∠2
∴ BF∥CE(内错角相等,两直线平行)
又∵ CE∥AM
∴ BF∥AM(平行于同一直线的两条直接平行)
例2 如图,已知直线a ∥b,直线c∥d,∠1=107°,
求∠2,∠3的度数.
解:∵ a ∥b,
∴∠2=∠1=107°
(两直线平行,内错角相等”).
∵c∥d,
∴∠1+∠3=180°
(两直线平行,同旁内角补)
∴∠3= 180°-∠1=180°-107°=73°.
如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
A.35° B.70°
C.90° D.110°
课堂小餐点1
D
例3 如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC
的度数.
E
A
B
C
D
2
1
CD
EF
1
2
1
2
80
80
70
70
150
F
解:过点E作EF//AB.
∵AB//CD,EF//AB(已知),
∴ // (平行于同一直线的两直线平行).
∴∠A+∠ =180o,∠C+∠ =180o(两直线平行,同旁内角互补).
又∵∠A=100°,∠C=110°(已知),
∴∠ = °, ∠ = °(等量代换).
∴∠AEC=∠1+∠2= °+ ° = °.
1、如图,C 岛在A岛的北偏东45°方 向,在B岛的北偏西25°方向,则从C 岛看A、B 两岛的视角∠ACB= .
2、如图,已知 , ,
则 ∠2= .
70°
20°
课堂小餐点2
拓展提升:如图,AB//CD,试解决下列问题:
(1)如图1,∠1+∠2=___;
(2)如图2,∠1+∠2+∠3=_ __;
(3)如图3,∠1+∠2+∠3+∠4=__ ;
(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n
= ;
180°
360°
540°
180°×(n-1)
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
课堂小总结
课后能量棒
作业内容见电子版资料。
基础修炼(必做):A组题、B组题;
挑战自我(选做):C组题。
加油!相信你们棒棒的!
平行线性质与判定的综合运用
第二章 相交线与平行线
北师版七年级下册数学
文字叙述
符号语言
图形
相等
两直线平行
∴a∥b
相等
两直线平行
∵
∴a∥b
互补
两直线平行
∴a∥b
同位角
内错角
同旁内角
∵∠1=∠2
∠3=∠2
∵∠2+∠4=180°
a
b
c
1
2
3
4
1.平行线的判定
回顾与思考
方法4:如图1,若a∥b,b∥c,则a∥c.
( )
方法5:如图2,若a⊥b,a⊥c,则b∥c.
( )
在同一平面内,平行于同一条直线的两条直线平行
在同一平面内,垂直于同一条直线的两条直线平行
2.平行线的其它判定方法
a
b
c
图1
a
b
c
图2
已知
结论
依据
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
3.平行线的性质
∠1=∠2
∠3=∠2
∠2+∠4
=180 °
例1 根据如图所示回答下列问题:
(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
典型例题
解:∠1与∠2是内错角,
若∠1=∠2,则可得BF∥CE
根据“内错角相等,两直线平行”
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
解:∠2与∠M是同位角,
若∠2=∠M,可得AM∥BF;
根据“同位角相等,两直线平行”
(3)若∠2 +∠3=180°,可以判定哪两条直线平
行?根据是什么?
解:∠2与∠3是同旁内角,
若∠2+∠3=180°,可得AC∥MD.
根据“同旁内角互补,两直线平行”。
(4)若∠1=∠2 ,CE∥AM,求证BF∥AM。
解:∵ ∠1=∠2
∴ BF∥CE(内错角相等,两直线平行)
又∵ CE∥AM
∴ BF∥AM(平行于同一直线的两条直接平行)
例2 如图,已知直线a ∥b,直线c∥d,∠1=107°,
求∠2,∠3的度数.
解:∵ a ∥b,
∴∠2=∠1=107°
(两直线平行,内错角相等”).
∵c∥d,
∴∠1+∠3=180°
(两直线平行,同旁内角补)
∴∠3= 180°-∠1=180°-107°=73°.
如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
A.35° B.70°
C.90° D.110°
课堂小餐点1
D
例3 如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC
的度数.
E
A
B
C
D
2
1
CD
EF
1
2
1
2
80
80
70
70
150
F
解:过点E作EF//AB.
∵AB//CD,EF//AB(已知),
∴ // (平行于同一直线的两直线平行).
∴∠A+∠ =180o,∠C+∠ =180o(两直线平行,同旁内角互补).
又∵∠A=100°,∠C=110°(已知),
∴∠ = °, ∠ = °(等量代换).
∴∠AEC=∠1+∠2= °+ ° = °.
1、如图,C 岛在A岛的北偏东45°方 向,在B岛的北偏西25°方向,则从C 岛看A、B 两岛的视角∠ACB= .
2、如图,已知 , ,
则 ∠2= .
70°
20°
课堂小餐点2
拓展提升:如图,AB//CD,试解决下列问题:
(1)如图1,∠1+∠2=___;
(2)如图2,∠1+∠2+∠3=_ __;
(3)如图3,∠1+∠2+∠3+∠4=__ ;
(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n
= ;
180°
360°
540°
180°×(n-1)
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
课堂小总结
课后能量棒
作业内容见电子版资料。
基础修炼(必做):A组题、B组题;
挑战自我(选做):C组题。
加油!相信你们棒棒的!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
