北师大版七下 1.5 平方差公式 课件(63张)
文档属性
| 名称 | 北师大版七下 1.5 平方差公式 课件(63张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 17:58:44 | ||
图片预览











文档简介
第一章 整式的乘除
北师大版数学七年级下册
1.平方差公式的推导和应用.
2.理解平方差公式的结构特征,灵活应用平方差公式.
学习目标
复习回顾:多项式与多项式是如何相乘的?
(a + b)( m + n)
=am
+an
+bm
+bn
导入新知
1
知识点
平方差公式
计算下列各题:
(1) (x+2) (x-2);(2) (1+3a) (1-3a );
(3) (x+5y) (x-5y);(4)(2y+z) (2y-z) .
观察以上算式及其运算结果,你有什么发现?
再举两例验证你的发现.
合作探究
平方差公式:
(1)平方差公式的推导:(a+b)(a-b)= =
.
(2)文字语言:两个数的和与这两个数的差的积,等于
这两个数的 .
(3)符号语言:(a+b)(a-b)= .
a2-ab+ab-b2
a2-b2
平方差
a2-b2
新知归纳
如图①,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸片拼成如图②的等腰梯形.
(1)设图①中阴影部分面积为S1,图②中阴影部分面积为S2,请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式.
例1
合作探究
导引:直先计算图①中阴影部分面积为S1=a2-b2,
再计算图②中阴影部分面积为S2= (2b+2a)
(a-b),然后根据面积相等得到乘法公式.
解:(1) S1=a2-b2,
S2= (2b+2a)(a-b) =(a+b)(a-b).
(2) (a+b)(a-b)= a2-b2.
平方差公式:
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,等于这两个数的平方差.
公式变形:
1、(a – b ) ( a + b) = a2-b2
2、(b + a )(-b + a ) = a2-b2
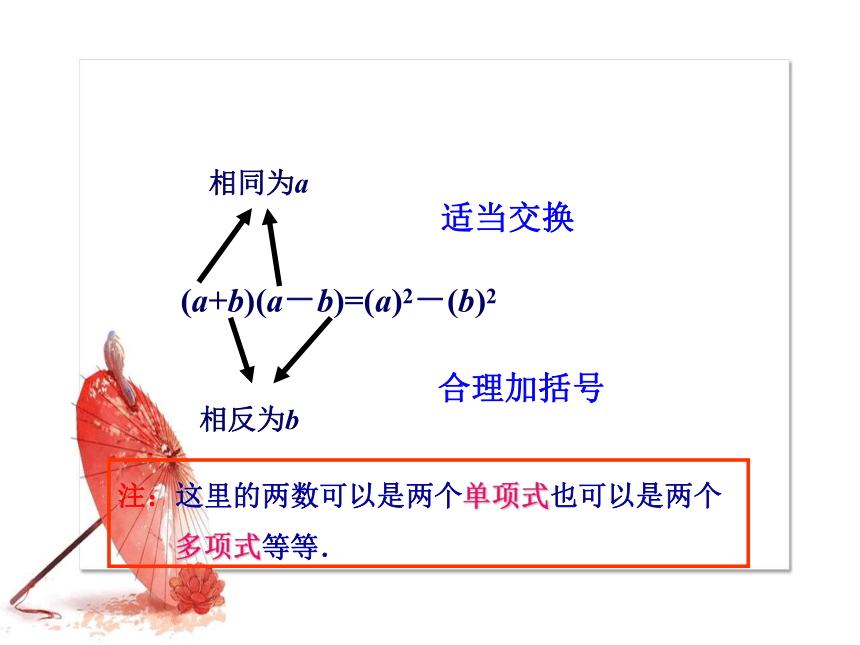
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b
注:这里的两数可以是两个单项式也可以是两个
多项式等等.
适当交换
合理加括号
例2 利用平方差公式计算:
(1) (5+6x)(5-6x);(2) (x-2y)(x+2y);
(3) (-m+n)(-m-n) .
解:(1) (5+6x)(5-6x)= 52-(6x)2=25-36x2;
(2) (x-2y)(x+2y)= x2-(2y)2= x2-4y2 ;
(3) (-m+n)(-m-n) = (-m)2-n2 = m2-n2 .
例3 利用平方差公式计算:
(1) ;(2) (ab+8)(ab-8) .
解:
(2) (ab+8)(ab-8) =(ab)2-64=a2b2-64.
1
计算:
(1) (a+2) (a-2); (2) (3a+2b) (3a-2b);
(3) (-x -1) (1-x) ;(4) (-4k+3) (-4k-3).
(1)(a+2)(a-2)=a2-22=a2-4.
(2)(3a+2b)(3a-2b)=(3a)2-(2b)2=9a2-4b2.
(3)(-x-1)(1-x)=(-x-1)(-x+1)
=(-x)2-12=x2-1.
(4)(-4k+3)(-4k-3)=(-4k)2-32=16k2-9.
解:
巩固新知
下列计算能运用平方差公式的是( )
A.(m+n)(-m-n)
B.(2x+3)(3x-2)
C.(5a2-b2c)(bc2+5a2)
D. ( m2- n3)(- m2- n3)
2
D
下列多项式乘法中,能用平方差公式计算的
是( )
A.(2a+b)(-2a+b)
B.(a+2)(2+a)
C.(-a+b)(a-b)
D.(a+b2)(a2-b)
3
A
4
【中考·衡阳】已知a+b=3,a-b=1,则a2-b2的值为________.
【中考·沈阳】下列运算正确的是( )
A.x3+x5=x8
B.x3+x5=x15
C.(x+1)(x-1)=x2-1
D.(2x)5=2x5
5
3
C
6
【中考·南平】下列运算正确的是( )
A.3x+2y=5xy
B.(m2)3=m5
C.(a+1)(a-1)=a2-1
D. =2
C
7
若(2x+3y)(mx-ny)=9y2-4x2,则( )
A.m=2,n=3
B.m=-2,n=-3
C.m=2,n=-3
D.m=-2,n=3
B
8
若x,y满足|x+y+5|+(x-y-9)2=0,则x2-y2的值为( )
A.14 B.-14
C.45 D.-45
D
9
如图①,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下部分沿虚线剪开拼成一个
梯形(如图②),利用这两个图形的面积,可以验证
的公式是( )
A.a2+b2=(a+b)(a-b)
B.a2-b2=(a+b)(a-b)
C.(a+b)2=a2+2ab+b2
D.(a-b)2=a2-2ab+b2
B
10
【中考·枣庄】如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分沿虚线剪开密铺成一个平行四边形,则该平行四
边形的面积为( )
A.a2+4
B.2a2+4a
C.3a2-4a-4
D.4a2-a-2
C
2
知识点
平方差公式的应用
(1)计算下列各组算式,并观察它们的共同特点:
(2)从以上的过程中,你发现了什么规律?
(3)请用字母表示这一规律,你能说明它的正确性吗?
7×9=
8×8=
11×13=
12×12=
79×81=
80×80=
合作探究
例4 用平方差公式进行计算:
(1)103×97; (2)118×122.
解:(1)103×97
=(100+3) (100-3)
=1002-32
=9 991 ;
(2)118×122
=(120-2) (100+2)
=1202-22
=14 396 .
例5 运用平方差公式计算:
(1) 2 014×2 016-2 0152;(2) 1.03×0.97;
(3) 40 ×39 .
导引:在(1)中,2 014与2 016都与2 015相差1,即
2 014=2 015-1,2 016=2 015+1;在(2)中1.03与
0.97都与1相差0.03,即1.03=1+0.03,0.97=1-0.03;
在(3)中40 与39 都与40相差 ,即40 =40+ ,
39 =40- ,因此可运用平方差公式进行计算.
解: (1)原式 =(2 015-1)(2 015+1)-2 0152
=2 0152-1-2 0152=-1;
(2)原式 =(1+0.03)(1-0.03) =12-0.032
=1-0.000 9=0.999 1;
(3)原式
本题运用了转化思想求解.运用平方差公式计算两数
乘积问题,关键是找到这两个数的平均数,再将原两
个数与这个平均数进行比较变形成两数的和与这两数
的差的积的形式,再用平方差公式可求解.
新知小结
例6 计算:
(1) a2(a+b)(a-b) +a2b2;(2) (2x-5)(2x+5)-2x (2x-3).
解:(1) a2(a+b)(a-b) +a2b2;
=a2(a2-b2) +a2b2
=a4-a2b2 +a2b2
=a4 ;
(2) (2x-5)(2x+5)-2x (2x-3).
= (2x)2-25-(4x2 -6x)
= 4x2-25-4x2 +6x
= 6x-25
合作探究
1
(1)704×696=(700+4)(700-4)=7002-42=489 984.
(2)(x+2y)(x-2y)+(x+1)(x-1)=x2-4y2+x2-1
=2x2-4y2-1.
(3)x(x-1)- =x2-x-
=x2-x-x2+ =-x+ .
解:
(1) 704×696 ;(2) (x+2y) (x-2y)+(x+1)(x-1);
(3) x(x-1)-(x- )(x+ ) .
巩固新知
2
计算2 0162-2 015×2 017的结果是( )
A.1 B.-1
C.2 D.-2
A
3
(1)499×501=(500-1)×(500+1)=5002-12
=250 000-1=249 999.
(2)60 ×59 = ×(60- )=602-
=3 600- =3 599 .
解:
计算:
(1)499×501;(2)60 ×59 ;
(3)99×101×10 001=(100-1)×(100+1)×10 001
=(1002-1)×10 001
=9 999×10 001
=(10 000-1)×(10 000+1)
=10 0002-1
=99 999 999.
解:
(3)99×101×10 001.
1. 平方差公式的特征:左边是两个二项式相乘,并
且这两个二项式有一项完全相同,另一项互为相
反数;右边是左边的相同项的平方减去互为相反
数的项的平方.
2. 公式(a+b)(a-b)=a2-b2中的字母a,b可以是单
项式,也可以是多项式.
3. 平方差公式可以逆用:a2-b2=(a+b)(a-b).
1
知识小结
归纳新知
下列运算正确的是( )
易错点:对平方差公式的特征理解不透而出错
2
易错小结
D
本题易错之处在于对平方差公式的左右结构特征没有认识清楚从而导致选错.
a2-b2
和
差
平方差
课后练习
C
D
B
C
C
24
1
1
9 999
B
D
D
C
【答案】B
二
去括号时没有变号
a2-b2
(a+b)(a-b)
【答案】a2 024-b2 024
an-bn
北师大版数学七年级下册
1.平方差公式的推导和应用.
2.理解平方差公式的结构特征,灵活应用平方差公式.
学习目标
复习回顾:多项式与多项式是如何相乘的?
(a + b)( m + n)
=am
+an
+bm
+bn
导入新知
1
知识点
平方差公式
计算下列各题:
(1) (x+2) (x-2);(2) (1+3a) (1-3a );
(3) (x+5y) (x-5y);(4)(2y+z) (2y-z) .
观察以上算式及其运算结果,你有什么发现?
再举两例验证你的发现.
合作探究
平方差公式:
(1)平方差公式的推导:(a+b)(a-b)= =
.
(2)文字语言:两个数的和与这两个数的差的积,等于
这两个数的 .
(3)符号语言:(a+b)(a-b)= .
a2-ab+ab-b2
a2-b2
平方差
a2-b2
新知归纳
如图①,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸片拼成如图②的等腰梯形.
(1)设图①中阴影部分面积为S1,图②中阴影部分面积为S2,请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式.
例1
合作探究
导引:直先计算图①中阴影部分面积为S1=a2-b2,
再计算图②中阴影部分面积为S2= (2b+2a)
(a-b),然后根据面积相等得到乘法公式.
解:(1) S1=a2-b2,
S2= (2b+2a)(a-b) =(a+b)(a-b).
(2) (a+b)(a-b)= a2-b2.
平方差公式:
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,等于这两个数的平方差.
公式变形:
1、(a – b ) ( a + b) = a2-b2
2、(b + a )(-b + a ) = a2-b2
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b
注:这里的两数可以是两个单项式也可以是两个
多项式等等.
适当交换
合理加括号
例2 利用平方差公式计算:
(1) (5+6x)(5-6x);(2) (x-2y)(x+2y);
(3) (-m+n)(-m-n) .
解:(1) (5+6x)(5-6x)= 52-(6x)2=25-36x2;
(2) (x-2y)(x+2y)= x2-(2y)2= x2-4y2 ;
(3) (-m+n)(-m-n) = (-m)2-n2 = m2-n2 .
例3 利用平方差公式计算:
(1) ;(2) (ab+8)(ab-8) .
解:
(2) (ab+8)(ab-8) =(ab)2-64=a2b2-64.
1
计算:
(1) (a+2) (a-2); (2) (3a+2b) (3a-2b);
(3) (-x -1) (1-x) ;(4) (-4k+3) (-4k-3).
(1)(a+2)(a-2)=a2-22=a2-4.
(2)(3a+2b)(3a-2b)=(3a)2-(2b)2=9a2-4b2.
(3)(-x-1)(1-x)=(-x-1)(-x+1)
=(-x)2-12=x2-1.
(4)(-4k+3)(-4k-3)=(-4k)2-32=16k2-9.
解:
巩固新知
下列计算能运用平方差公式的是( )
A.(m+n)(-m-n)
B.(2x+3)(3x-2)
C.(5a2-b2c)(bc2+5a2)
D. ( m2- n3)(- m2- n3)
2
D
下列多项式乘法中,能用平方差公式计算的
是( )
A.(2a+b)(-2a+b)
B.(a+2)(2+a)
C.(-a+b)(a-b)
D.(a+b2)(a2-b)
3
A
4
【中考·衡阳】已知a+b=3,a-b=1,则a2-b2的值为________.
【中考·沈阳】下列运算正确的是( )
A.x3+x5=x8
B.x3+x5=x15
C.(x+1)(x-1)=x2-1
D.(2x)5=2x5
5
3
C
6
【中考·南平】下列运算正确的是( )
A.3x+2y=5xy
B.(m2)3=m5
C.(a+1)(a-1)=a2-1
D. =2
C
7
若(2x+3y)(mx-ny)=9y2-4x2,则( )
A.m=2,n=3
B.m=-2,n=-3
C.m=2,n=-3
D.m=-2,n=3
B
8
若x,y满足|x+y+5|+(x-y-9)2=0,则x2-y2的值为( )
A.14 B.-14
C.45 D.-45
D
9
如图①,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下部分沿虚线剪开拼成一个
梯形(如图②),利用这两个图形的面积,可以验证
的公式是( )
A.a2+b2=(a+b)(a-b)
B.a2-b2=(a+b)(a-b)
C.(a+b)2=a2+2ab+b2
D.(a-b)2=a2-2ab+b2
B
10
【中考·枣庄】如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分沿虚线剪开密铺成一个平行四边形,则该平行四
边形的面积为( )
A.a2+4
B.2a2+4a
C.3a2-4a-4
D.4a2-a-2
C
2
知识点
平方差公式的应用
(1)计算下列各组算式,并观察它们的共同特点:
(2)从以上的过程中,你发现了什么规律?
(3)请用字母表示这一规律,你能说明它的正确性吗?
7×9=
8×8=
11×13=
12×12=
79×81=
80×80=
合作探究
例4 用平方差公式进行计算:
(1)103×97; (2)118×122.
解:(1)103×97
=(100+3) (100-3)
=1002-32
=9 991 ;
(2)118×122
=(120-2) (100+2)
=1202-22
=14 396 .
例5 运用平方差公式计算:
(1) 2 014×2 016-2 0152;(2) 1.03×0.97;
(3) 40 ×39 .
导引:在(1)中,2 014与2 016都与2 015相差1,即
2 014=2 015-1,2 016=2 015+1;在(2)中1.03与
0.97都与1相差0.03,即1.03=1+0.03,0.97=1-0.03;
在(3)中40 与39 都与40相差 ,即40 =40+ ,
39 =40- ,因此可运用平方差公式进行计算.
解: (1)原式 =(2 015-1)(2 015+1)-2 0152
=2 0152-1-2 0152=-1;
(2)原式 =(1+0.03)(1-0.03) =12-0.032
=1-0.000 9=0.999 1;
(3)原式
本题运用了转化思想求解.运用平方差公式计算两数
乘积问题,关键是找到这两个数的平均数,再将原两
个数与这个平均数进行比较变形成两数的和与这两数
的差的积的形式,再用平方差公式可求解.
新知小结
例6 计算:
(1) a2(a+b)(a-b) +a2b2;(2) (2x-5)(2x+5)-2x (2x-3).
解:(1) a2(a+b)(a-b) +a2b2;
=a2(a2-b2) +a2b2
=a4-a2b2 +a2b2
=a4 ;
(2) (2x-5)(2x+5)-2x (2x-3).
= (2x)2-25-(4x2 -6x)
= 4x2-25-4x2 +6x
= 6x-25
合作探究
1
(1)704×696=(700+4)(700-4)=7002-42=489 984.
(2)(x+2y)(x-2y)+(x+1)(x-1)=x2-4y2+x2-1
=2x2-4y2-1.
(3)x(x-1)- =x2-x-
=x2-x-x2+ =-x+ .
解:
(1) 704×696 ;(2) (x+2y) (x-2y)+(x+1)(x-1);
(3) x(x-1)-(x- )(x+ ) .
巩固新知
2
计算2 0162-2 015×2 017的结果是( )
A.1 B.-1
C.2 D.-2
A
3
(1)499×501=(500-1)×(500+1)=5002-12
=250 000-1=249 999.
(2)60 ×59 = ×(60- )=602-
=3 600- =3 599 .
解:
计算:
(1)499×501;(2)60 ×59 ;
(3)99×101×10 001=(100-1)×(100+1)×10 001
=(1002-1)×10 001
=9 999×10 001
=(10 000-1)×(10 000+1)
=10 0002-1
=99 999 999.
解:
(3)99×101×10 001.
1. 平方差公式的特征:左边是两个二项式相乘,并
且这两个二项式有一项完全相同,另一项互为相
反数;右边是左边的相同项的平方减去互为相反
数的项的平方.
2. 公式(a+b)(a-b)=a2-b2中的字母a,b可以是单
项式,也可以是多项式.
3. 平方差公式可以逆用:a2-b2=(a+b)(a-b).
1
知识小结
归纳新知
下列运算正确的是( )
易错点:对平方差公式的特征理解不透而出错
2
易错小结
D
本题易错之处在于对平方差公式的左右结构特征没有认识清楚从而导致选错.
a2-b2
和
差
平方差
课后练习
C
D
B
C
C
24
1
1
9 999
B
D
D
C
【答案】B
二
去括号时没有变号
a2-b2
(a+b)(a-b)
【答案】a2 024-b2 024
an-bn
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
