5.3.2 角平分线的性质及画法(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 5.3.2 角平分线的性质及画法(知识清单+经典例题+夯实基础+提优特训+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 489.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 16:53:06 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版2020﹣2021学年度下学期七年级数学下册第五章生活中的轴对称
5.3
简单的轴对称图形
第三课时
角平分线的性质及画法
【知识清单】
角平分线的性质:
1.角是轴对称图形,角平分线所在的直线是它的对称轴;
2.角平分线上的点到这个角的两边的距离相等.
【经典例题】
例题1、用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SAS
B.ASA
C.SSS
D.AAS
【考点】全等三角形的判定;作图—基本作图.
【分析】连接DC,EC,根据SSS证△ODC≌△OEC,即可推出答案.
【解答】连接DC,EC,
在△ODC和△OEC中
∵,
∴△ODC≌△OEC(SSS),
∴∠AOC=∠BOC,
故选:C.
【点评】本题考查了全等三角形的性质和判定的应用,培养学生运用性质进行推理的能力,题型较好,难度适中.
例题2、如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=11,DE=4,求△BCE的面积
【考点】角平分线的性质.?
【分析】作EF⊥BC于F,根据角平分线的性质定理
得到FE=DE=4,根据三角形面积公式计算即可.
【解答】过点E,作EF⊥BC于F,
∵BE平分∠ABC,EF⊥BC,ED⊥AB,
∴EF=DE=4,
∴△BCE的面积=BC·EF=×11×4=22.
【点评】本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.
【夯实基础】
1.已知OP是∠MON的平分线,且点A在OP上,下图中线段AB和AC一定相等的是(
)
2.如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下确定P点的
方法正确的是(?
)
A.点P为∠A、∠B两角平分线的交点
B.点P为AC、AB两边上的高的交点
C.点P为∠A的平分线与边AB的垂直平分线的交点
D.点P为AC、AB两边的垂直平分线的交点
3.如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,过点D作DE⊥AB,垂足为E,
则下列结论错误的是(
)
A.DE=DC
B.∠ADE=∠ABC
C.BE=BC
D.∠ADE=∠ABD
4.如图,在△ABC中,BP,CP分别是∠ABC,∠ACB的平分线,交点为P,PD⊥AC于D,PE⊥AB于E,PD=5,
BC=18.则△PBC
的面积为
(
)
?A.22.5?
B.32.5
?C.35
?D.45
5.如图是三条两两相交的笔直公路,某物流公司现要修建一个货物中转站,使它到三条公路的距离相等,这个货物中转站可选择的位置共有_____
个.
6.点P是△ABC三个角的平分线的交点,若AB=30cm,BC=50
cm,AC=60
cm,
则S△PAB︰S△PBC︰S△PAC=
.
7.如图,在△ABC中,点P是AC上一点,
连接BP,求作一点M,使得点M到AB和AC
两边的距离相等,并且到点B和点P的距离相等.
(不写作法,保留作图痕迹)
作图,如图所示:
8.如图,BD平分∠ABC,DE垂直于AB于E点,△ABC的面积等于96,AB+BC=48,
求
DE的长.
9.已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、D.
(1)PC和PD有怎样的数量关系是________;
(2)请你证明(1)得出的结论.
【提优特训】
10.如图所示,已知∠AOB,求作射线OC,使OC平分∠AOB,作法的合理顺序是(
)
(将①②③重新排列)①作射线OC;②以O为圆心,任意长为半径画弧交OA、OB于D、E;③分别以D、E为圆心,大于DE的长为半径作弧,在∠AOB内,两弧交于点C
.
A.①②③
B.③②①
C.②①③
D.②③①
11.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC,交BC于D,过点D作DE⊥AB于点E,若AB=17,则△DEB的周长为(
)
A.8.5
B.17
C.34
D.51
12.如图所示,△ABC的角平分线AD将BC边分成2︰3两部分.若AC=6cm,则AB=
(
)
A.2
B.3
C.4
D.
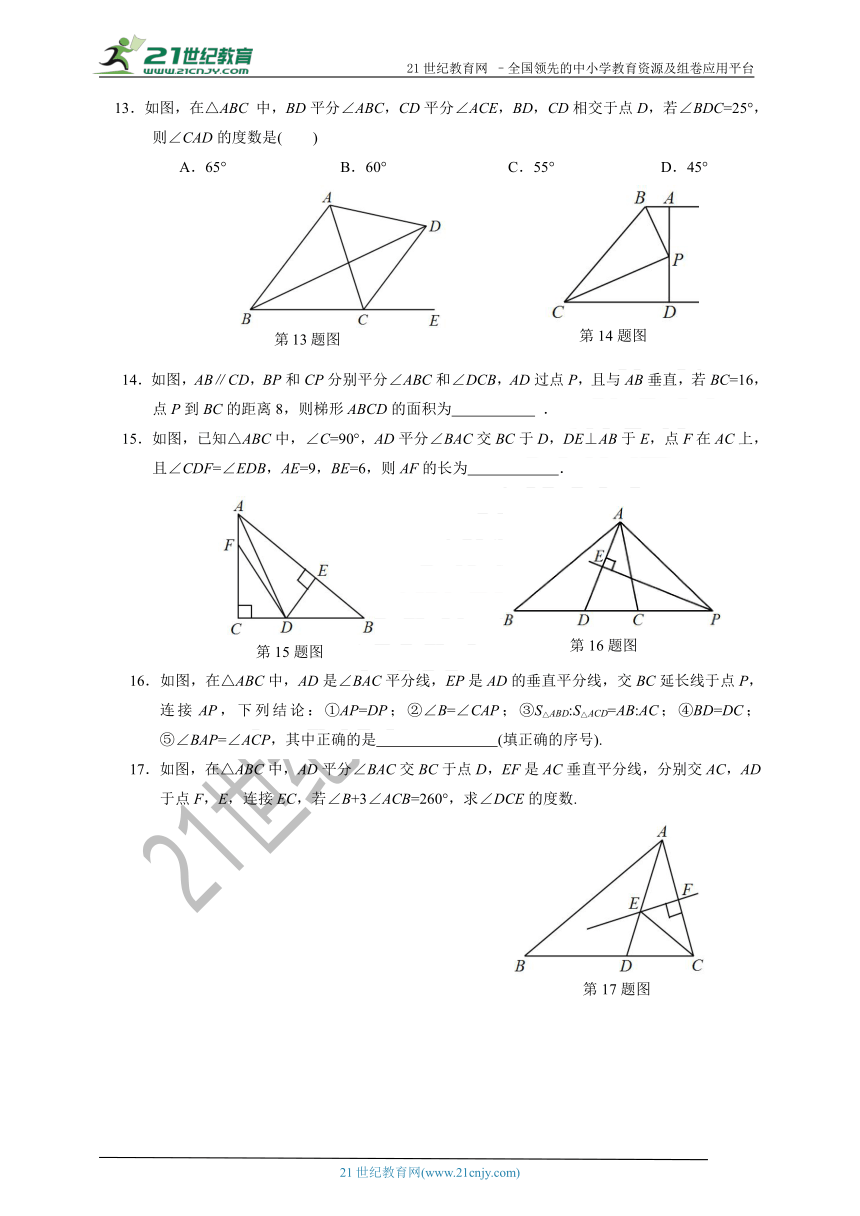
13.如图,在△ABC
中,BD平分∠ABC,CD平分∠ACE,BD,CD相交于点D,若∠BDC=25°,则∠CAD的度数是(
)
A.65°
B.60°
C.55°
D.45°
14.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若BC=16,点P到BC的距离8,则梯形ABCD的面积为
.
15.如图,已知△ABC中,∠C=90°,AD平分∠BAC交BC于D,DE⊥AB于E,点F在AC上,且∠CDF=∠EDB,AE=9,BE=6,则AF的长为
.
16.如图,在△ABC中,AD是∠BAC平分线,EP是AD的垂直平分线,交BC延长线于点P,连接AP,下列结论:①AP=DP;②∠B=∠CAP;③S△ABD:S△ACD=AB:AC;④BD=DC;⑤∠BAP=∠ACP,其中正确的是
(填正确的序号).
17.如图,在△ABC中,AD平分∠BAC交BC于点D,EF是AC垂直平分线,分别交AC,AD于点F,E,连接EC,若∠B+3∠ACB=260°,求∠DCE的度数.
18.如图,点P为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且PM=PN,∠BMP+∠BNP=180°.BP平分∠ABC吗?说明理由.
【中考链接】
19.(2020年?怀化)如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为E.若BD=3,则DE的长为
(
)
A.3
B.
C.2
D.6
20.(2020年?湘潭)
如图,点P是∠AOC的角平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为
.
参考答案
1、C
2、C
3、D
4、D
5、4
6、3:5:6
10、D
11、B
12、C
13、A
14、128
15、3
16、①②③⑤
19、A
20、3
7.如图,在△ABC中,点P是AC上一点,
连接BP,求作一点M,使得点M到AB和AC
两边的距离相等,并且到点B和点P的距离相等.
(不写作法,保留作图痕迹)
作图,如图所示:
8.如图,BD平分∠ABC,DE垂直于AB于E点,△ABC的面积等于96,AB+BC=48,
求
DE的长.
解:∵BD平分∠ABC,DE垂直于AB于E点,
∴点D到BC的距离等于DE的长度,
∴S△ABC=S△ABD+S△BCD
=AB·DE+BC·DE
=DE(AB
+
BC)
=×48·DE=24DE,
∵△ABC的面积等于96,
∴24DE=96,
解得DE=4.
9.已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、D.
(1)PC和PD有怎样的数量关系是________;
(2)请你证明(1)得出的结论.
解:(1)PC=PD.
?
(2)过P分别作PE⊥OB于E,PF⊥OA于F,
∴∠CFP=∠DEP=90°,
∵OM是∠AOB的平分线,
∴PE=PF,
∵∠1+∠FPD=90°,
又∵∠AOB=90°,
∴∠FPE=90°,
∴∠2+∠FPD=90°,
∴∠1=∠2,
在△CFP和△DEP中
?
?∵,
∴△CFP≌△DEP(ASA),
∴PC=PD.
17.如图,在△ABC中,AD平分∠BAC交BC于点D,EF是AC垂直平分线,分别交AC,AD于点F,E,连接EC,若∠B+3∠ACB=260°,求∠DCE的度数.
解:∵EF是AC垂直平分线,
∴AE=CE,
∴∠EAC=∠ECA,
∵AD平分∠BAC,
∴∠BAD=∠CAD=∠BAC,
∴∠ECA=∠BAC=(180°?∠B?∠ACD),
∴∠DCE=∠ACD?∠ECA
=∠ACD?∠BAC
=∠ACD?(180°?∠B?∠ACD)
=∠B+∠ACD?90°
=,
∵∠B+3∠ACB=260°,
∴∠DCE==40.
18.如图,点P为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且PM=PN,∠BMP+∠BNP=180°.BP平分∠ABC吗?说明理由.
解:如图所示:在BC上截取ND=BM,
∵∠BMP+∠BNP=180°,∠BNP+∠DNP=180°,
∴∠BMP
=∠DNP,
在△BMP与△DNP中,
∵?,
∴△BMP≌△DNP(SAS),
∴∠MBP=∠NDP,BP=DP,
∴∠PBD=∠PDB,
∴∠MBP
=∠PDB,
∴BP平分∠ABC.
例题2图
第15题图
例题1图
A
B
C
D
第18题图
第14题图
第12题图
第3题图
第4题图
第7题图
第9题图
例题2图
例题1图
第17题图
第13题图
第11题图
第10题图
第19题图
第20题图
第16题图
第5题图
第18题图
第17题图
第9题图
第8题图
第8题图
第7题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版2020﹣2021学年度下学期七年级数学下册第五章生活中的轴对称
5.3
简单的轴对称图形
第三课时
角平分线的性质及画法
【知识清单】
角平分线的性质:
1.角是轴对称图形,角平分线所在的直线是它的对称轴;
2.角平分线上的点到这个角的两边的距离相等.
【经典例题】
例题1、用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SAS
B.ASA
C.SSS
D.AAS
【考点】全等三角形的判定;作图—基本作图.
【分析】连接DC,EC,根据SSS证△ODC≌△OEC,即可推出答案.
【解答】连接DC,EC,
在△ODC和△OEC中
∵,
∴△ODC≌△OEC(SSS),
∴∠AOC=∠BOC,
故选:C.
【点评】本题考查了全等三角形的性质和判定的应用,培养学生运用性质进行推理的能力,题型较好,难度适中.
例题2、如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=11,DE=4,求△BCE的面积
【考点】角平分线的性质.?
【分析】作EF⊥BC于F,根据角平分线的性质定理
得到FE=DE=4,根据三角形面积公式计算即可.
【解答】过点E,作EF⊥BC于F,
∵BE平分∠ABC,EF⊥BC,ED⊥AB,
∴EF=DE=4,
∴△BCE的面积=BC·EF=×11×4=22.
【点评】本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.
【夯实基础】
1.已知OP是∠MON的平分线,且点A在OP上,下图中线段AB和AC一定相等的是(
)
2.如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下确定P点的
方法正确的是(?
)
A.点P为∠A、∠B两角平分线的交点
B.点P为AC、AB两边上的高的交点
C.点P为∠A的平分线与边AB的垂直平分线的交点
D.点P为AC、AB两边的垂直平分线的交点
3.如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,过点D作DE⊥AB,垂足为E,
则下列结论错误的是(
)
A.DE=DC
B.∠ADE=∠ABC
C.BE=BC
D.∠ADE=∠ABD
4.如图,在△ABC中,BP,CP分别是∠ABC,∠ACB的平分线,交点为P,PD⊥AC于D,PE⊥AB于E,PD=5,
BC=18.则△PBC
的面积为
(
)
?A.22.5?
B.32.5
?C.35
?D.45
5.如图是三条两两相交的笔直公路,某物流公司现要修建一个货物中转站,使它到三条公路的距离相等,这个货物中转站可选择的位置共有_____
个.
6.点P是△ABC三个角的平分线的交点,若AB=30cm,BC=50
cm,AC=60
cm,
则S△PAB︰S△PBC︰S△PAC=
.
7.如图,在△ABC中,点P是AC上一点,
连接BP,求作一点M,使得点M到AB和AC
两边的距离相等,并且到点B和点P的距离相等.
(不写作法,保留作图痕迹)
作图,如图所示:
8.如图,BD平分∠ABC,DE垂直于AB于E点,△ABC的面积等于96,AB+BC=48,
求
DE的长.
9.已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、D.
(1)PC和PD有怎样的数量关系是________;
(2)请你证明(1)得出的结论.
【提优特训】
10.如图所示,已知∠AOB,求作射线OC,使OC平分∠AOB,作法的合理顺序是(
)
(将①②③重新排列)①作射线OC;②以O为圆心,任意长为半径画弧交OA、OB于D、E;③分别以D、E为圆心,大于DE的长为半径作弧,在∠AOB内,两弧交于点C
.
A.①②③
B.③②①
C.②①③
D.②③①
11.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC,交BC于D,过点D作DE⊥AB于点E,若AB=17,则△DEB的周长为(
)
A.8.5
B.17
C.34
D.51
12.如图所示,△ABC的角平分线AD将BC边分成2︰3两部分.若AC=6cm,则AB=
(
)
A.2
B.3
C.4
D.
13.如图,在△ABC
中,BD平分∠ABC,CD平分∠ACE,BD,CD相交于点D,若∠BDC=25°,则∠CAD的度数是(
)
A.65°
B.60°
C.55°
D.45°
14.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若BC=16,点P到BC的距离8,则梯形ABCD的面积为
.
15.如图,已知△ABC中,∠C=90°,AD平分∠BAC交BC于D,DE⊥AB于E,点F在AC上,且∠CDF=∠EDB,AE=9,BE=6,则AF的长为
.
16.如图,在△ABC中,AD是∠BAC平分线,EP是AD的垂直平分线,交BC延长线于点P,连接AP,下列结论:①AP=DP;②∠B=∠CAP;③S△ABD:S△ACD=AB:AC;④BD=DC;⑤∠BAP=∠ACP,其中正确的是
(填正确的序号).
17.如图,在△ABC中,AD平分∠BAC交BC于点D,EF是AC垂直平分线,分别交AC,AD于点F,E,连接EC,若∠B+3∠ACB=260°,求∠DCE的度数.
18.如图,点P为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且PM=PN,∠BMP+∠BNP=180°.BP平分∠ABC吗?说明理由.
【中考链接】
19.(2020年?怀化)如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为E.若BD=3,则DE的长为
(
)
A.3
B.
C.2
D.6
20.(2020年?湘潭)
如图,点P是∠AOC的角平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为
.
参考答案
1、C
2、C
3、D
4、D
5、4
6、3:5:6
10、D
11、B
12、C
13、A
14、128
15、3
16、①②③⑤
19、A
20、3
7.如图,在△ABC中,点P是AC上一点,
连接BP,求作一点M,使得点M到AB和AC
两边的距离相等,并且到点B和点P的距离相等.
(不写作法,保留作图痕迹)
作图,如图所示:
8.如图,BD平分∠ABC,DE垂直于AB于E点,△ABC的面积等于96,AB+BC=48,
求
DE的长.
解:∵BD平分∠ABC,DE垂直于AB于E点,
∴点D到BC的距离等于DE的长度,
∴S△ABC=S△ABD+S△BCD
=AB·DE+BC·DE
=DE(AB
+
BC)
=×48·DE=24DE,
∵△ABC的面积等于96,
∴24DE=96,
解得DE=4.
9.已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、D.
(1)PC和PD有怎样的数量关系是________;
(2)请你证明(1)得出的结论.
解:(1)PC=PD.
?
(2)过P分别作PE⊥OB于E,PF⊥OA于F,
∴∠CFP=∠DEP=90°,
∵OM是∠AOB的平分线,
∴PE=PF,
∵∠1+∠FPD=90°,
又∵∠AOB=90°,
∴∠FPE=90°,
∴∠2+∠FPD=90°,
∴∠1=∠2,
在△CFP和△DEP中
?
?∵,
∴△CFP≌△DEP(ASA),
∴PC=PD.
17.如图,在△ABC中,AD平分∠BAC交BC于点D,EF是AC垂直平分线,分别交AC,AD于点F,E,连接EC,若∠B+3∠ACB=260°,求∠DCE的度数.
解:∵EF是AC垂直平分线,
∴AE=CE,
∴∠EAC=∠ECA,
∵AD平分∠BAC,
∴∠BAD=∠CAD=∠BAC,
∴∠ECA=∠BAC=(180°?∠B?∠ACD),
∴∠DCE=∠ACD?∠ECA
=∠ACD?∠BAC
=∠ACD?(180°?∠B?∠ACD)
=∠B+∠ACD?90°
=,
∵∠B+3∠ACB=260°,
∴∠DCE==40.
18.如图,点P为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且PM=PN,∠BMP+∠BNP=180°.BP平分∠ABC吗?说明理由.
解:如图所示:在BC上截取ND=BM,
∵∠BMP+∠BNP=180°,∠BNP+∠DNP=180°,
∴∠BMP
=∠DNP,
在△BMP与△DNP中,
∵?,
∴△BMP≌△DNP(SAS),
∴∠MBP=∠NDP,BP=DP,
∴∠PBD=∠PDB,
∴∠MBP
=∠PDB,
∴BP平分∠ABC.
例题2图
第15题图
例题1图
A
B
C
D
第18题图
第14题图
第12题图
第3题图
第4题图
第7题图
第9题图
例题2图
例题1图
第17题图
第13题图
第11题图
第10题图
第19题图
第20题图
第16题图
第5题图
第18题图
第17题图
第9题图
第8题图
第8题图
第7题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
