充要条件

(共22张PPT)
旧知温习
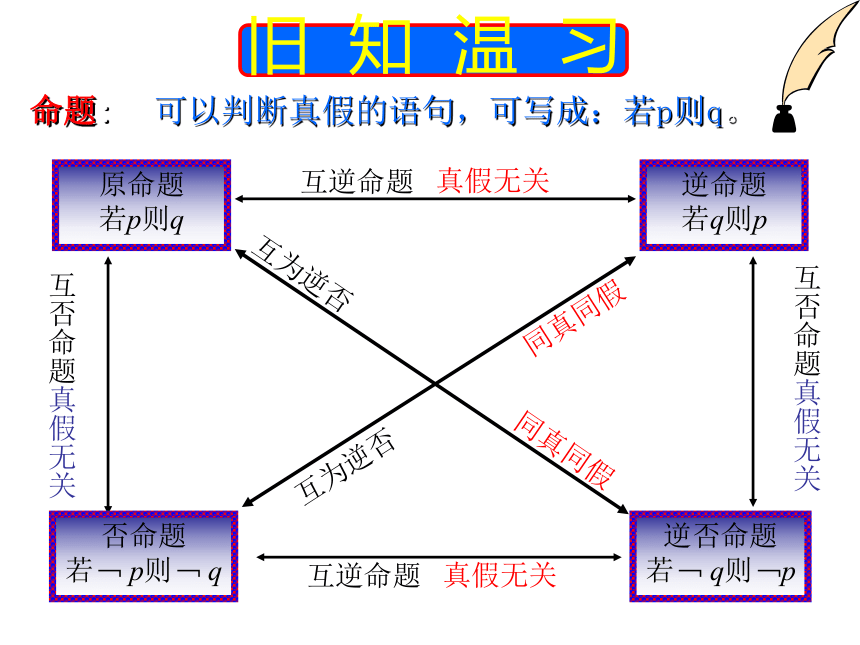
原命题
若p则q
逆命题
若q则p
否命题
若﹁ p则﹁ q
逆否命题
若﹁ q则﹁p
互为逆否 同真同假
互为逆否 同真同假
互逆命题 真假无关
互逆命题 真假无关
互否命题真假无关
互否命题真假无关
可以判断真假的语句，可写成：若p则q。
命题:
符号
与
的介绍
如果命题为真，即如果p成立，那么q一定成立，
记作 ，读作 “ p推出 q ”．
p
q
如果命题为假，即如果p成立，那么q不成立，
记作 ，读作 “ p推不出 q ”．
p
q
现有命题“若p则q”，
新知准备
1
２
３
４
５
６
７
x >0
x =
√2
两三角形全等
a、b为奇数
ab >0
=
a
2
b
2
c
2
+
- 2x - 3 = 0
x
2
>0
x
2
= 2
x
2
两三角形面积相等
a + b为偶数
a >0且
b >0
以a、b、c 为三边 ,且c为最大边的三角形是RtΔ
= -1
x
A
B
A
B
B
A
下面两栏中的A与B之间存在何种关系？
（1）哪些A
B？
（2）哪些B
A？
（3）哪些既能
又能
？
新知传授
6
答案：
（2）B
A ：
A
B
B
（3）既能
A ：
又能
1
２
３
４
５
６
７
x >0
x =
√2
两三角形全等
a、b为奇数
ab >0
=
a
2
b
2
c
2
+
- 2x - 3 = 0
x
2
>0
x
2
= 2
x
2
两三角形面积相等
a + b为偶数
a >0且
b >0
以a、b、c 为三边 ,且c为最大边的三角形是RtΔ
= -1
x
A
B
（1）A
B ：
1
2
3
4
（6）
7
5
（6）
观察
1、2 、3、4
观察
5、7
充分条件的定义
必要条件的定义
如果A成立时，B必然成立，即 ，我们就说，A是B成立的充分条件．（即为使B成立，只需条件A就够了）
A
B
如果B成立时，A必然成立，即 ，我们就说，A是B成立的必要条件．（即为使B成立，就必须条件A成立）
B
A
观察
6
充要条件的定义
如果A成立时，B必然成立，即 ，而且B成立时，A也必然成立，即 ．
这时我们就说，A是B成立的充分必要条件，简称A是B的充要条件，记作 或 ．
A
B
B
A
A
B
B
A
当 ，而且 ．
这时我们就说，A是B的既不充分也不必要条件 ．
B
A
A
B
（1） p：x=y， q： ．
=
x
2
y
2
例1．
指出下列各组命题中，p是q的什么条件，q是p的什么条件：
x=y
=
x
2
y
2
由 ，即 ，
知p是q的充分条件，q是 p的必要条件．
p
q
解：
由 ，
即三角形的三边相等 三角形的三个角相等，
知p是q的充分条件，q是 p的必要条件；
p
q
（2） p：三角形的三边均相等，q：三角形的三个角均相等．
q
p
　　反过来，
　　由 　 ，
即三角形的三个角相等 三角形的三条边相等，
知q是p的充分条件，p是q的必要条件．
因此，p与q互为充要条件．
解：
1．用符号“ ”与“ ”填空：
(1) x = 0 xy = 0.
(2) xy = 0 x = 0.
(3) 两个角相等 两个角是对顶角.
(4) 两个角是对顶角 两个角相等.
2．下列各组命题中，p是q的什么条件，q是p的什么条件：
(1) p：a ∈ Q ，q： a ∈ R ．
(2) p：a ∈ R ，q： a ∈ Q ．
(3) p：内错角相等，q：两直线平行．
(4) p：两直线平行，q：内错角相等．
Key : p 是q 的充分条件
q 是p 的必要条件
Key : p 是q 的必要条件
q 是p 的充分条件
Key : p 是q 的充分条件
q 是p 的必要条件（充要条件）
Key : p 是q 的充分条件
q 是p 的必要条件（充要条件）
例1、判断下列命题是真命题还是假命题，并研究其逆命题的真假，用推出符号表示结论。 （1）若x=y，则x2=y2。 （2）有两角相等的三角形是等腰三角形。 （3）ax2+ax+1>0的解集为R，则0b2，则a>b。
答：
(1) p q ,
q p
(2) p q ,
q p
(3) p q ,
q p
(4) p q ,
q p
二.新课讲解
基 础 知 识
1.若P=>Q且Q≠>P，则P是Q的充分而不必要条件,
2.若P≠>Q且Q=>P，则P是Q的必要而不充分条件,
3.若P=>Q且Q=>P，则P是Q的充要条件，
4.若P≠>Q且Q≠>P，则P既不是Q的充分条件，也不是Q的必要条件。(既不充分也不必要条件）
(1) p：(x - 2)(x - 3) = 0 ; q：x – 2 = 0．
(2) p：同位角相等 ; q：两直线平行．
(3) p： x = 3 ; q： ．
(4) p：四边形的对角线相等，q：四边形是平行四边形．
x
2
= 9
例2．
指出下列各组命题中，p是q的什么条件(在“充分而不必要
条件”、“必要而不充分条件”、“充要条件”、“既不充分
也不必要”中选出一种)？
x – 2 = 0 (x – 2)(x - 3) = 0 ，
(x – 2)(x - 3) = 0 x – 2 = 0．
所以p是q的必要而不充分条件．
同位角相等 两直线平行．
所以p是q的充要条件．
(1) p：(x - 2)(x - 3) = 0 ; q：x – 2 = 0．
解：
(2) p：同位角相等 ; q：两直线平行．
解：
(4) p：四边形的对角线相等，q：四边形是平行四边形．
x = 3 ， ，
所以p是q的充分而不必要条件．
x
2
= 9
= 3
x
x
2
= 9
四边形的对角线相等 四边形是平行四边形，
四边形是平行四边形 四边形的对角线相等．　
所以p是q的既不充分也不必要条件．
x
2
= 9
(3) p： x = 3 ; q： ．
解：
解：
从“充分而不必要条件”、“必要而不充分条件”、“充要
条件”或“既不充分也不必要条件”中选出适当的一种填空：
(1) “ A B ” 是 “ A∩B = A ” 的 ．
(2) “ x∈A ” 是 “ x∈A∩B ” 的 ．
(3) “ a=b=0 ” 是 “ ab=0 ” 的 ．
(4) “ 0(5) “ 二次函数 的图象过原点 ” 是
“ c = 0 ” 的 ．
y=
+bx + c（a ≠ 0）
ax
2
充分而不必要条件
必要而不充分条件
充分而不必要条件
充分而不必要条件
充要条件
应 用
充分条件
定 义
充要条件
必要条件
新
知
小
结
作业布置
二、生活中的一些名言警句包含着充要关系，
如：“骄兵必败”、“玉不琢，不成器”、
“若要人不知，除非己莫为”等等．
请大家自己试着找一些，分析其充要关系
三、课后作业：优化方案P30—P32 基础与提升
一、P36 — P37，
习题1．8，第１、2题
由B是C的充分条件可得，B C
由D是C的必要条件可得，C D
由D是B的充分条件可得，D B
由A是C的充分条件可得，A C
A
D
C
B
因而可得，
(1) D是C的充要条件．
(2) A是B的充分而不必要条件．
设A是C的充分条件，B是C的充分条件，D是C的必要条件，
D是B的充分条件，则
(1) D是C的什么条件？
(2) A是B的什么条件？
解：
机动例题
1
已知“ p：m<- 3 , q：方程 无实根”,
指出p是q的什么条件？
= 0
m
- x -
x
2
= 0
m
- x -
x
2
方程 无实根，则
1
4
Δ= (- 1) –4·1· (- m) = 1 + 4m < 0
即m < -　．
2
= 0
m
- x -
x
2
∴m < -３ 方程 　 无实根．　
∴p是q的充分条件．
= 0
m
- x -
x
2
∵方程 无实根
m < -３，　
∴p不是q的必要条件．
∴综上所述，p是q的充分而不必要条件．
解：
机动例题
2