18.2.3平行四边形的判定-2020-2021学年华东师大版八年级数学下册课件(17张)
文档属性
| 名称 | 18.2.3平行四边形的判定-2020-2021学年华东师大版八年级数学下册课件(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 715.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 21:37:11 | ||
图片预览




文档简介
(共17张PPT)
18.2
平行四边形的判定
第18章
平行四边形
教学目标
教学重点与难点
重点:平行四边形的判定定理及其应用.
难点:灵活利用平行四边形的判定定理解题.
1.探索并掌握平行四边形的判定定理.
2.能灵活运用平行四边形的判定定理解题.
3.体会数学的转化思想.
平行四边形的判定
方法一(定义):两组对边分别平行的四边形.
方法二(判定定理1):两组对边分别相等的四边形.
方法三(判定定理2):一组对边平行且相等的四边形.
∵
AB
∥
CD,BC
∥
AD,
∴四边形ABCD是平行四边形.
∵
AB
=
CD,BC
=AD,
∴四边形ABCD是平行四边形.
∵
AB
∥
CD且AB
=
CD,(或AD
∥
BC且AD
=
BC)
∴四边形ABCD是平行四边形.
D
A
B
C
O
方法四(判定定理3):对角线互相平分的四边形.
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
温故夯基
1.在四边形ABCD中,从(1)AB∥CD
,(2)BC∥AD,
(3)AB=CD,(4)BC=AD.这四个条件中任选两个,
能使四边形ABCD是平行四边形的选法有(
).
A.
3种
B.
4种
C.
5种
D.
6种
2.不能判定四边形ABCD是平行四边形的条件是(
).
A
.AB=CD
,AD=BC
B
.AB∥CD
,
AB=CD
C.AB=CD
,
AD∥BC
C.AB∥CD
,
AD∥
BC
B
C
巩固练习
3.在四边形ABCD中,已知AB=CD
.
请补充一个条件:
,使得四边形ABCD是平行四边形.
AB∥CD
或AD=BC
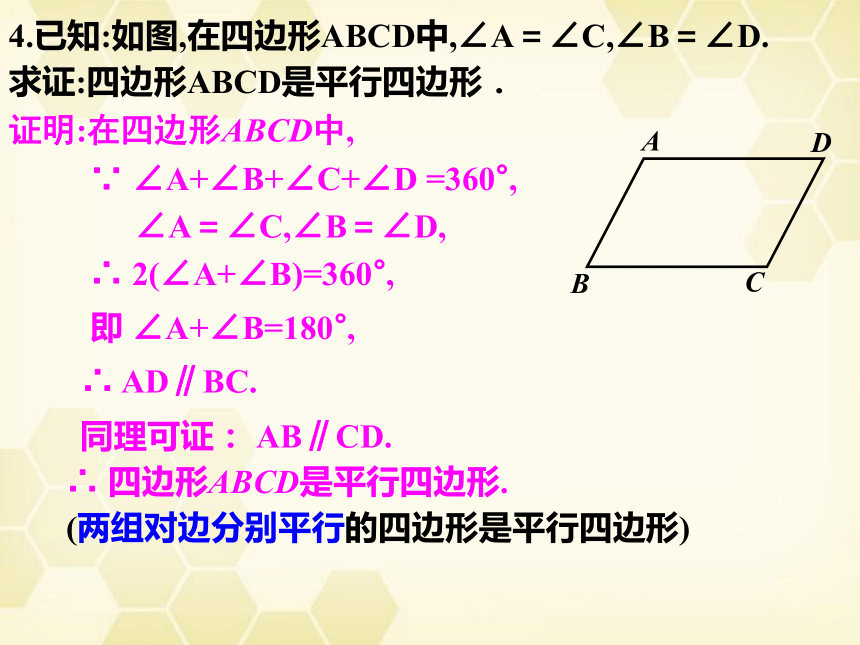
4.已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
D
A
B
C
证明:在四边形ABCD中,
∵
∠A+∠B+∠C+∠D
=360°,
∠A=∠C,∠B=∠D,
∴
2(∠A+∠B)=360°,
即
∠A+∠B=180°,
∴
AD∥BC.
同理可证:
AB∥CD.
∴
四边形ABCD是平行四边形.
(两组对边分别平行的四边形是平行四边形)
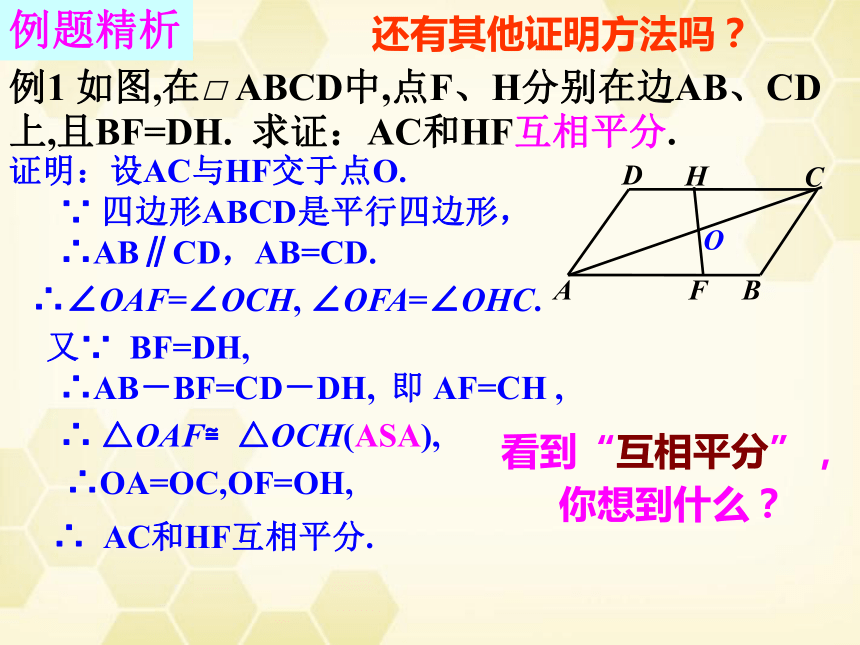
例1
如图,在□
ABCD中,点F、H分别在边AB、CD上,且BF=DH.
求证:AC和HF互相平分.
C
D
A
B
F
H
证明:设AC与HF交于点O.
∵
四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵
BF=DH,
∴AB-BF=CD-DH,
即
AF=CH
,
∴OA=OC,OF=OH,
∴
AC和HF互相平分.
O
例题精析
∴∠OAF=∠OCH,
∠OFA=∠OHC.
∴
△OAF≌△OCH(ASA),
还有其他证明方法吗?
看到“互相平分”,
你想到什么?
例题精析
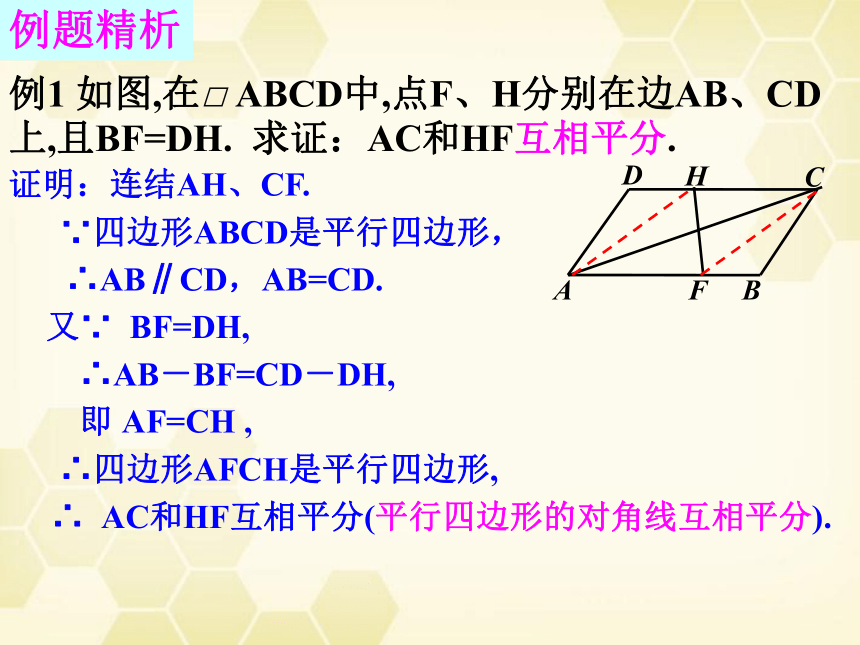
例1
如图,在□
ABCD中,点F、H分别在边AB、CD上,且BF=DH.
求证:AC和HF互相平分.
C
D
A
B
F
H
证明:连结AH、CF.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵
BF=DH,
∴AB-BF=CD-DH,
即
AF=CH
,
∴四边形AFCH是平行四边形,
∴
AC和HF互相平分(平行四边形的对角线互相平分).
如图,
在□ABCD中,AF=CH,DE=BG
.
求证:EG与HF互相平分.
随堂练习
证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,
AD=BC,AB=DC,
又∵AF=CH,DE=BG,
∴
AE=CG,FB=DH,
同理可证:EH=FG,
∴
四边形EFGH是平行四边形.
∴
EG和HF互相平分.
在△AEF与△CGH中,
AF=CH,
∠A=∠C,
AE=CG,
∴△AEF≌△CGH(SAS),
∴EF=GH.
例2
四边形AEFD和EBCF都是平行四边形.
求证:四边形ABCD
是平行四边形.
A
B
C
D
E
F
证明:∵四边形AEFD是平行四边形,
又∵四边形EBCF是平行四边形,
∴
四边形ABCD是平行四边形.
例题精析
∥
∴
AD=EF.
∥
∴
BC=EF.
∥
∴
AD=BC.
(一组对边平行且相等的四边形是平行四边形)
例3
如图,G、H是□ABCD对角线AC上的两点,
且AG=CH,E、F分别是边AB、CD的中点.
(1)判断四边形EHFG的形状,并加以证明;
D
A
B
C
E
F
H
G
O
(2)试问EH和GF有何关系,请加以证明.
证明:(1)四边形EHFG是平行四边形.
连结EF交AC于点O.
连结对角线是研究
平行四边形时常用
的作辅助线的方法
∵四边形AEFD是平行四边形,
∥
∴
AB=CD.
∵
E、F分别是边AB、CD的中点,
∴AE=CF.
又
∵AB∥CD,
∴∠EAO=∠FCO.
又∵∠AOE=∠COF,
∴△AOE≌△COF(AAS),
∴OA=OC,OE=OF,
又
∵AG=CH,
∴OG=OH,
∴四边形EHFG是平行四边形.
(对角线互相平分的四边形是平行四边形)
EH=GF
随堂练习
1.如图,四边形ABCD是平行四边形,AE、CF分别与直线DB
相交于点E和点F,且AE∥CF,分别连结点C、E和点A、F.
求证:四边形AFCE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADF=∠CBE,
∴
∠ADE=∠CBF,
∵AE∥CF,
∴∠AED=∠CFB,
∴△ADE≌△CBF,
∴AE=CF,
∵AE∥CF,
∴四边形AFCE为平行四边形.
在△ADE与△CBF中,
∠ADE=∠CBF,
∠AED=∠CFB,
AD=CB,
(一组对边平行且相等的四边形是平行四边形)
还有其他证明方法吗?
随堂练习
1.如图,四边形ABCD是平行四边形,AE、CF分别与直线DB
相交于点E和点F,且AE∥CF,分别连结点C、E和点A、F.
求证:四边形AFCE是平行四边形.
O
证明:连结AC交EF于点O.
∵四边形ABCD是平行四边形,
∴OA=OC.
∵AE∥CF,
∴∠AEO=∠CFO,
又∵
∠AOE=∠COF,
∴
△AOE≌△COF,
∴OE=OF.
∵OA=OC,OE=OF,
∴四边形AFCE为平行四边形.
(对角线互相平分的四边形是平行四边形)
2.如图,□ABCD的对角线AC与BD相交于点O,直线EF过
点O,且与AB、DC分别相交于点E和点F,直线GH过点O
且与AD、BC分别相交于点G和点H.
求证:四边形GEHF是平行四边形.
A
E
B
C
F
D
证明:∵四边形ABCD
是平行四边形,
∴
OA
=
OC,AD∥CB.
∴∠OAE
=∠OCF.
又∵∠AOE
=∠COF,
∴△AOE
≌△COF
(ASA),
∴OE
=
OF.
同理可证:OG
=
OH.
∴四边形
GEHF是平行四边形.
(对角线互相平分的四边形是平行四边形)
3.如图,□ABCD的对角线AC、BD相交于点O,EF经过点O
且分别交AB、CD于点E、F,点G、H分别为OA、OC的
中点.
求证:四边形EHFG是平行四边形.
证明:∵四边形ABCD
是平行四边形,
∴
OA
=
OC,AB∥CD.
∴∠OAE
=∠OCF.
又∵∠AOE
=∠COF,
∴△AOE
≌△COF
(ASA),
∴OE
=
OF.
∵点G、H分别为OA、OC的中点,OA=OC,
∴OG
=
OH.
∴四边形
EHFG是平行四边形.
(对角线互相平分的四边形是平行四边形)
平行四边形的判定
方法一(定义):两组对边分别平行的四边形.
方法二(判定定理1):两组对边分别相等的四边形.
方法三(判定定理2):一组对边平行且相等的四边形.
∵
AB
∥
CD,BC
∥
AD,
∴四边形ABCD是平行四边形.
∵
AB
=
CD,BC
=AD,
∴四边形ABCD是平行四边形.
∵
AB
∥
CD且AB
=
CD,(或AD
∥
BC且AD
=
BC)
∴四边形ABCD是平行四边形.
D
A
B
C
O
方法四(判定定理3):对角线互相平分的四边形.
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
课堂小结
作业与练习
书面作业:课本P90
习题18.2
3,4,5
练习:学习检测
P57-60
1至17
预习任务
预习课本P98-101
19.1.1
矩形的性质
教学反思
作业存在的主要问题
18.2
平行四边形的判定
第18章
平行四边形
教学目标
教学重点与难点
重点:平行四边形的判定定理及其应用.
难点:灵活利用平行四边形的判定定理解题.
1.探索并掌握平行四边形的判定定理.
2.能灵活运用平行四边形的判定定理解题.
3.体会数学的转化思想.
平行四边形的判定
方法一(定义):两组对边分别平行的四边形.
方法二(判定定理1):两组对边分别相等的四边形.
方法三(判定定理2):一组对边平行且相等的四边形.
∵
AB
∥
CD,BC
∥
AD,
∴四边形ABCD是平行四边形.
∵
AB
=
CD,BC
=AD,
∴四边形ABCD是平行四边形.
∵
AB
∥
CD且AB
=
CD,(或AD
∥
BC且AD
=
BC)
∴四边形ABCD是平行四边形.
D
A
B
C
O
方法四(判定定理3):对角线互相平分的四边形.
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
温故夯基
1.在四边形ABCD中,从(1)AB∥CD
,(2)BC∥AD,
(3)AB=CD,(4)BC=AD.这四个条件中任选两个,
能使四边形ABCD是平行四边形的选法有(
).
A.
3种
B.
4种
C.
5种
D.
6种
2.不能判定四边形ABCD是平行四边形的条件是(
).
A
.AB=CD
,AD=BC
B
.AB∥CD
,
AB=CD
C.AB=CD
,
AD∥BC
C.AB∥CD
,
AD∥
BC
B
C
巩固练习
3.在四边形ABCD中,已知AB=CD
.
请补充一个条件:
,使得四边形ABCD是平行四边形.
AB∥CD
或AD=BC
4.已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
D
A
B
C
证明:在四边形ABCD中,
∵
∠A+∠B+∠C+∠D
=360°,
∠A=∠C,∠B=∠D,
∴
2(∠A+∠B)=360°,
即
∠A+∠B=180°,
∴
AD∥BC.
同理可证:
AB∥CD.
∴
四边形ABCD是平行四边形.
(两组对边分别平行的四边形是平行四边形)
例1
如图,在□
ABCD中,点F、H分别在边AB、CD上,且BF=DH.
求证:AC和HF互相平分.
C
D
A
B
F
H
证明:设AC与HF交于点O.
∵
四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵
BF=DH,
∴AB-BF=CD-DH,
即
AF=CH
,
∴OA=OC,OF=OH,
∴
AC和HF互相平分.
O
例题精析
∴∠OAF=∠OCH,
∠OFA=∠OHC.
∴
△OAF≌△OCH(ASA),
还有其他证明方法吗?
看到“互相平分”,
你想到什么?
例题精析
例1
如图,在□
ABCD中,点F、H分别在边AB、CD上,且BF=DH.
求证:AC和HF互相平分.
C
D
A
B
F
H
证明:连结AH、CF.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵
BF=DH,
∴AB-BF=CD-DH,
即
AF=CH
,
∴四边形AFCH是平行四边形,
∴
AC和HF互相平分(平行四边形的对角线互相平分).
如图,
在□ABCD中,AF=CH,DE=BG
.
求证:EG与HF互相平分.
随堂练习
证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,
AD=BC,AB=DC,
又∵AF=CH,DE=BG,
∴
AE=CG,FB=DH,
同理可证:EH=FG,
∴
四边形EFGH是平行四边形.
∴
EG和HF互相平分.
在△AEF与△CGH中,
AF=CH,
∠A=∠C,
AE=CG,
∴△AEF≌△CGH(SAS),
∴EF=GH.
例2
四边形AEFD和EBCF都是平行四边形.
求证:四边形ABCD
是平行四边形.
A
B
C
D
E
F
证明:∵四边形AEFD是平行四边形,
又∵四边形EBCF是平行四边形,
∴
四边形ABCD是平行四边形.
例题精析
∥
∴
AD=EF.
∥
∴
BC=EF.
∥
∴
AD=BC.
(一组对边平行且相等的四边形是平行四边形)
例3
如图,G、H是□ABCD对角线AC上的两点,
且AG=CH,E、F分别是边AB、CD的中点.
(1)判断四边形EHFG的形状,并加以证明;
D
A
B
C
E
F
H
G
O
(2)试问EH和GF有何关系,请加以证明.
证明:(1)四边形EHFG是平行四边形.
连结EF交AC于点O.
连结对角线是研究
平行四边形时常用
的作辅助线的方法
∵四边形AEFD是平行四边形,
∥
∴
AB=CD.
∵
E、F分别是边AB、CD的中点,
∴AE=CF.
又
∵AB∥CD,
∴∠EAO=∠FCO.
又∵∠AOE=∠COF,
∴△AOE≌△COF(AAS),
∴OA=OC,OE=OF,
又
∵AG=CH,
∴OG=OH,
∴四边形EHFG是平行四边形.
(对角线互相平分的四边形是平行四边形)
EH=GF
随堂练习
1.如图,四边形ABCD是平行四边形,AE、CF分别与直线DB
相交于点E和点F,且AE∥CF,分别连结点C、E和点A、F.
求证:四边形AFCE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADF=∠CBE,
∴
∠ADE=∠CBF,
∵AE∥CF,
∴∠AED=∠CFB,
∴△ADE≌△CBF,
∴AE=CF,
∵AE∥CF,
∴四边形AFCE为平行四边形.
在△ADE与△CBF中,
∠ADE=∠CBF,
∠AED=∠CFB,
AD=CB,
(一组对边平行且相等的四边形是平行四边形)
还有其他证明方法吗?
随堂练习
1.如图,四边形ABCD是平行四边形,AE、CF分别与直线DB
相交于点E和点F,且AE∥CF,分别连结点C、E和点A、F.
求证:四边形AFCE是平行四边形.
O
证明:连结AC交EF于点O.
∵四边形ABCD是平行四边形,
∴OA=OC.
∵AE∥CF,
∴∠AEO=∠CFO,
又∵
∠AOE=∠COF,
∴
△AOE≌△COF,
∴OE=OF.
∵OA=OC,OE=OF,
∴四边形AFCE为平行四边形.
(对角线互相平分的四边形是平行四边形)
2.如图,□ABCD的对角线AC与BD相交于点O,直线EF过
点O,且与AB、DC分别相交于点E和点F,直线GH过点O
且与AD、BC分别相交于点G和点H.
求证:四边形GEHF是平行四边形.
A
E
B
C
F
D
证明:∵四边形ABCD
是平行四边形,
∴
OA
=
OC,AD∥CB.
∴∠OAE
=∠OCF.
又∵∠AOE
=∠COF,
∴△AOE
≌△COF
(ASA),
∴OE
=
OF.
同理可证:OG
=
OH.
∴四边形
GEHF是平行四边形.
(对角线互相平分的四边形是平行四边形)
3.如图,□ABCD的对角线AC、BD相交于点O,EF经过点O
且分别交AB、CD于点E、F,点G、H分别为OA、OC的
中点.
求证:四边形EHFG是平行四边形.
证明:∵四边形ABCD
是平行四边形,
∴
OA
=
OC,AB∥CD.
∴∠OAE
=∠OCF.
又∵∠AOE
=∠COF,
∴△AOE
≌△COF
(ASA),
∴OE
=
OF.
∵点G、H分别为OA、OC的中点,OA=OC,
∴OG
=
OH.
∴四边形
EHFG是平行四边形.
(对角线互相平分的四边形是平行四边形)
平行四边形的判定
方法一(定义):两组对边分别平行的四边形.
方法二(判定定理1):两组对边分别相等的四边形.
方法三(判定定理2):一组对边平行且相等的四边形.
∵
AB
∥
CD,BC
∥
AD,
∴四边形ABCD是平行四边形.
∵
AB
=
CD,BC
=AD,
∴四边形ABCD是平行四边形.
∵
AB
∥
CD且AB
=
CD,(或AD
∥
BC且AD
=
BC)
∴四边形ABCD是平行四边形.
D
A
B
C
O
方法四(判定定理3):对角线互相平分的四边形.
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
课堂小结
作业与练习
书面作业:课本P90
习题18.2
3,4,5
练习:学习检测
P57-60
1至17
预习任务
预习课本P98-101
19.1.1
矩形的性质
教学反思
作业存在的主要问题
