2020-2021学年华东师大版八年级数学下册19.1.1矩形的性质(27张ppt)课件
文档属性
| 名称 | 2020-2021学年华东师大版八年级数学下册19.1.1矩形的性质(27张ppt)课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 13:11:48 | ||
图片预览


文档简介
(共27张PPT)
19.1.1
矩形的性质
第19章
矩
形、菱形与正方形
教学目标
教学重点与难点
重点:矩形的性质及其应用.
难点:灵活利用矩形的性质解题.
1.探索并掌握矩形的性质.
2.能灵活运用矩形的性质,进行计算和证明.
3.体会数学的推理和转化思想.
平行四边形
A
B
C
D
四边形
A
B
C
D
AD//BC,DC//AB
一般
特殊
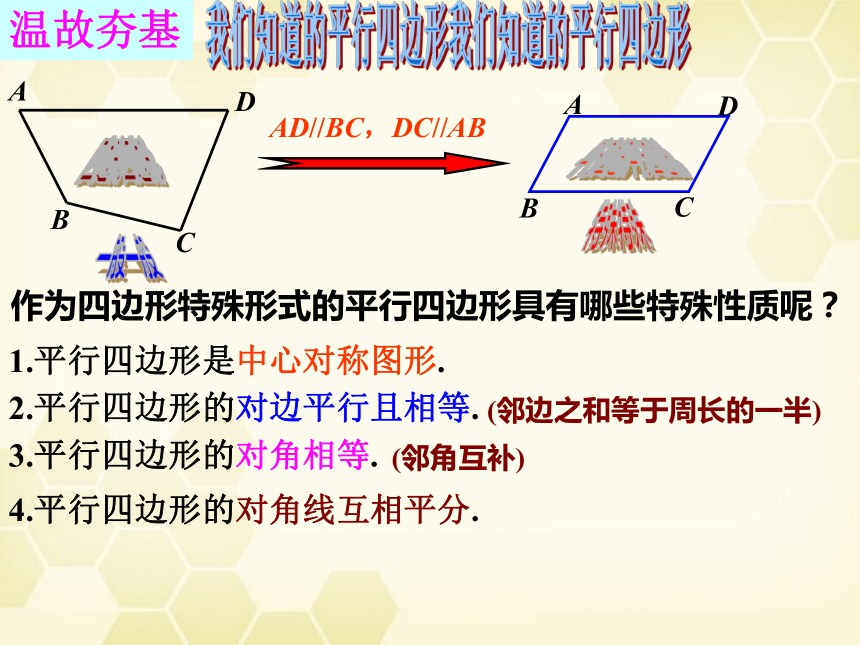
温故夯基
我们知道的平行四边形
作为四边形特殊形式的平行四边形具有哪些特殊性质呢?
1.平行四边形是中心对称图形.
2.平行四边形的对边平行且相等.
(邻边之和等于周长的一半)
3.平行四边形的对角相等.
(邻角互补)
4.平行四边形的对角线互相平分.
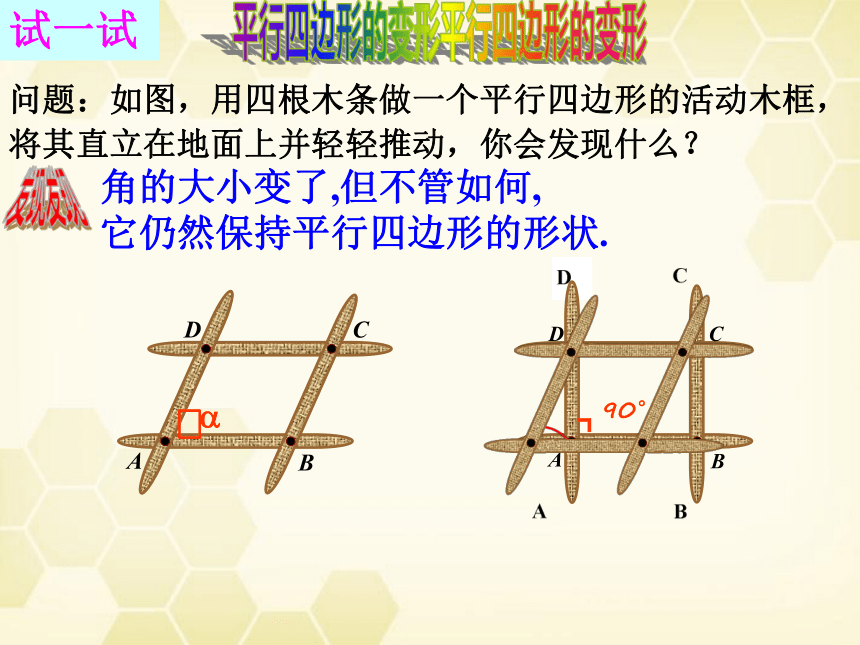
问题:如图,用四根木条做一个平行四边形的活动木框,将其直立在地面上并轻轻推动,你会发现什么?
平行四边形的变形
D
A
C
B
D
A
C
B
?
┓
90°
发现
角的大小变了,但不管如何,
它仍然保持平行四边形的形状.
我是平行四边形的特殊形式—矩形!
试一试
A
B
C
D
平行四边形
有一个角是直角
A
B
C
D
矩形
在□ABCD中,∠A=90。,
∴
四边形ABCD是矩形.
学习新知
一.矩形的定义:
有一个角是直角的平行四边形是矩形.
几何语言:
矩形是特殊的平行四边形,特殊在有一个角是直角!
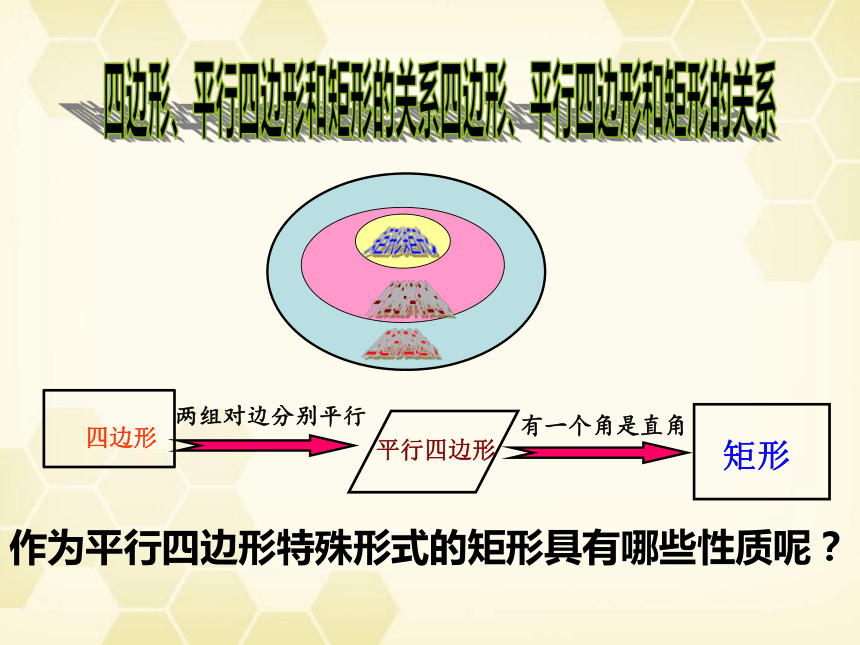
四边形、平行四边形和矩形的关系
四边形
平行四边形
矩形
两组对边分别平行
有一个角是直角
四边形
平行四边形
矩形
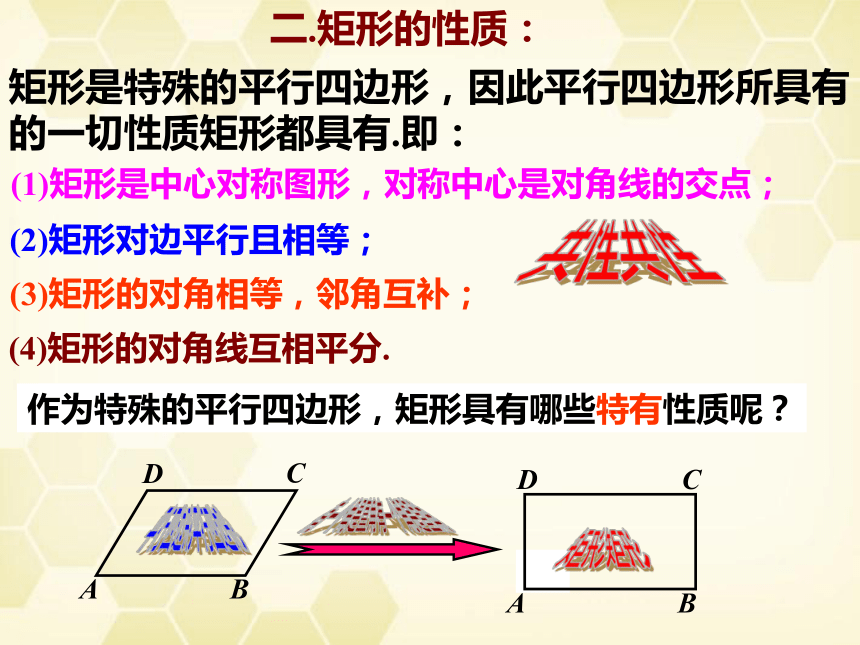
作为平行四边形特殊形式的矩形具有哪些性质呢?
二.矩形的性质:
A
B
C
D
平行四边形
有一个角是直角
A
B
C
D
矩形
矩形是特殊的平行四边形,因此平行四边形所具有
的一切性质矩形都具有.即:
(1)矩形是中心对称图形,对称中心是对角线的交点;
(2)矩形对边平行且相等;
(3)矩形的对角相等,邻角互补;
(4)矩形的对角线互相平分.
共性
作为特殊的平行四边形,矩形具有哪些特有性质呢?
是
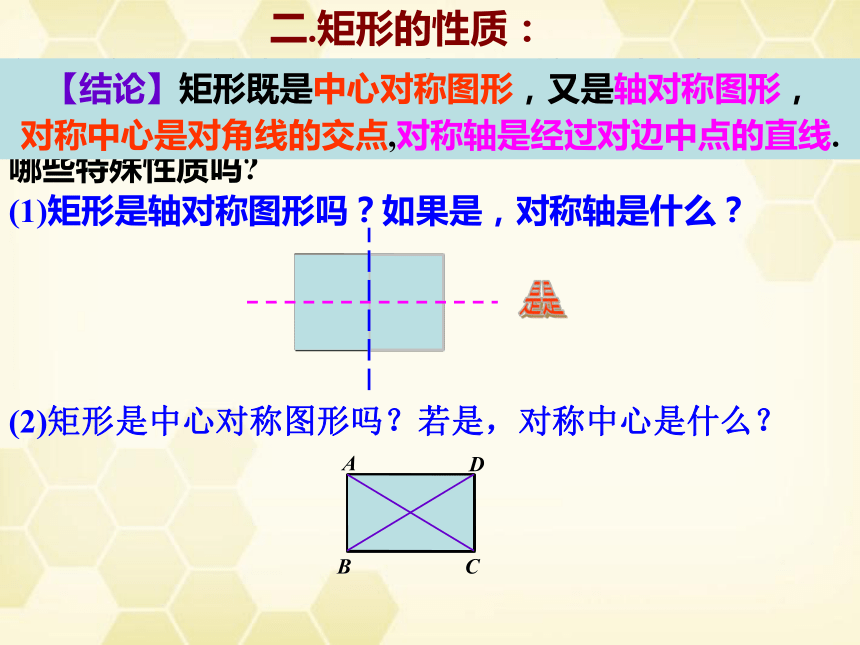
(2)矩形是中心对称图形吗?若是,对称中心是什么?
B
C
D
A
O
二.矩形的性质:
问题:矩形是特殊的平行四边形,因此矩形除具有平行
四边形的性质外,还有它的特殊性质。你能说出矩形有
哪些特殊性质吗?
(1)矩形是轴对称图形吗?如果是,对称轴是什么?
【结论】矩形既是中心对称图形,又是轴对称图形,
对称中心是对角线的交点,对称轴是经过对边中点的直线.
D
A
C
B
O
D
A
C
B
┓
O
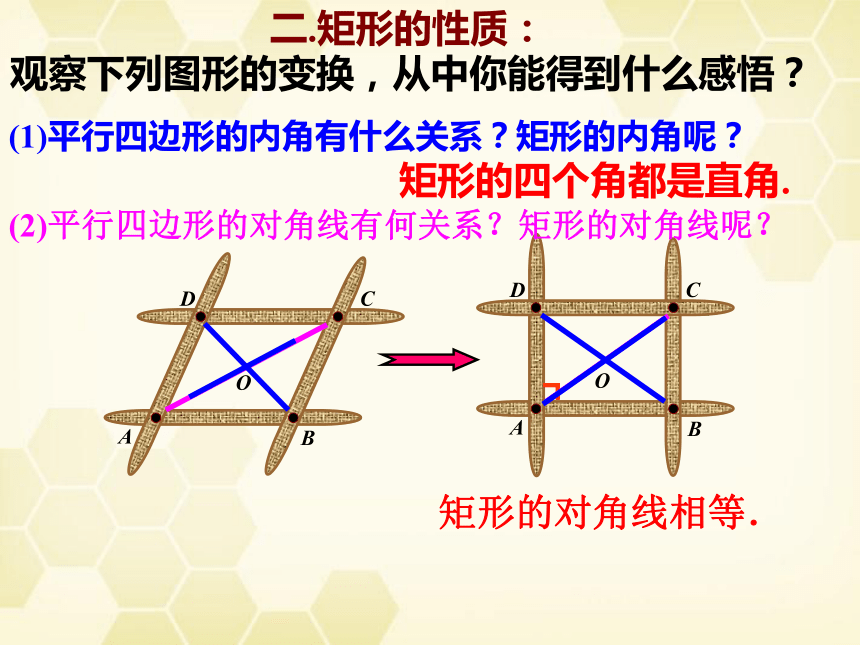
(2)平行四边形的对角线有何关系?矩形的对角线呢?
二.矩形的性质:
观察下列图形的变换,从中你能得到什么感悟?
(1)平行四边形的内角有什么关系?矩形的内角呢?
矩形的四个角都是直角.
矩形的对角线相等.
二.矩形的性质:
矩形的性质定理1
矩形的四个角都是直角.
A
B
C
D
矩形
几何语言:
∵
四边形ABCD是矩形,
∴
∠A=∠B=∠C=∠D=90°.
矩形的性质定理2
矩形的对角线相等.
几何语言:
∵
四边形ABCD是矩形,
∴
AC=BD.
平行四边形、矩形对比理解
对称性
边
角
对角线
平行四边形的一般性性质
矩形的
特殊性质
对边平行
且相等
邻边
垂直
四个角
都是直角
中心对称
图形
既是中心对称图形又是轴对称图形
对角相等
邻角互补
对角线
互相平分
对角线
相等
对比归纳
例1
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,矩形的对角线长
是13cm,那么该矩形的周长是多少?
解:
∵
△AOB、
△BOC、
△COD
和△AOD四个三角形的周长和为86cm,
例题精析
∴
AB+BC+CD+DA+2(OA+OB+OC+OD)
=AB+BC+CD+DA+2(AC+BD)=86.
又∵AC=BD=13cm,
∴
AB+BC+CD+DA=86-2(AC+BD)
=86-4×13
=34(cm),
即矩形ABCD的周长等于34cm.
例2
如图,在矩形ABCD中,点E在边CD上.将该矩形沿AE
折叠,恰好使点D落在边BC上的点F处,如果∠BAF=60°,
求∠DAE的大小.
C
D
B
A
F
E
解:∵四边形ABCD是矩形,
∴
∠BAD=90°.
∵
∠BAF=60°,
∴
∠FAD=30°.
又∵△DAE沿AE折叠得到△FAE,
∴
∠DAE=∠FAE=
=15°.
B
D
随堂练习
1.矩形具有而平行四边行不具有的的性质是(
).
A.
对角相等
B.
对角线相等
C.
对角线互相平分
D.
对边平行且相等
2.矩形的一条对角线与一边的夹角为40°,
则两条对角线相交所成的锐角是(
).
A.
20°
B.
40°
C.
60°
D.
80°
3.在矩形ABCD中,对角线AC,BD交于点O,
下列说法错误的是(
).
A.
AB∥DC
B.
AC=BD
C.
AC⊥BD
D.
OA=OB
C
4.如图,矩形ABCD的顶点A,C分别在直线a,b上,且a//b,∠1=60°,则∠2的度数为(
).
A.
60°
B.
30°
C.
45°
D.
75°
A
B
C
D
a
b
1
2
5.如图,在矩形ABCD中,E为BC边的中点,∠AEC的平分线交AD边于点F,若AB=3,AD=8,则FD的长为(
).
A.
1
B.
2
C.
3
D.
4
D
A
B
C
E
F
A
C
(4)
(5)
6.将长方形ABCD的纸片沿EF折成如图所示,
?EFG=55°,则?FGE=
.
A
D'
C'
F
B
D
C
E
G
70°
7.将矩形ABCD的纸片沿EF折叠后,ED与BC的交点为G,
点D、
C分别落在D'
、C'的位置上,若∠EFG=60°,
则∠1=
,∠2=
.
1
2
A
B
C
D
E
F
C'
D'
G
(6)
(7)
60°
120°
例题精析
例3
如图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,
垂足为点E.试求BE的长.
A
B
C
D
E
┏
解:在矩形ABCD在,∠ABC=90°,
例4
如图,在矩形ABCD中,对角线AC与BD交于点O,
AE垂直且平分线段BO,垂足为点E,BD=15cm.
求AC、AB的长.
∟
A
B
C
D
O
E
解:∵四边形ABCD是矩形,
∴
AC=BD=15,
∵AE垂直平分BO,
∴AB=AO=7.5
.
即AC的长为15cm,AB的长为7.5cm
.
若∠AOD=120。,AB=4,求AC、AD及矩形的面积.
例4
如图,在矩形ABCD中,对角线AC与BD交于点O,
AE垂直且平分线段BO,垂足为点E,BD=15cm.
∟
A
B
C
D
O
E
解:∵四边形ABCD是矩形,
∴
AC=BD,
若∠AOD=120。,AB=4,求AC、AD及矩形的面积.
∵∠AOD=120。,
∴∠AOB=60。,
∴△AOB为等边三角形,
∴
AB=AO=BO=4,
∴
AC=BD=2AO=8.
∵∠BAD=90。,
∴矩形的面积为AB.AD
1.如图,在矩形的ABCD中,E是AD边上一点,
试说明△BCE的面积与矩形ABCD的面积之间的关系.
A
B
C
D
E
随堂练习
┏
F
解:过点E作EF⊥BC于点F,
∵四边形ABCD是矩形,
∴∠A=∠ABC=90。.
∵
EF⊥BC,
∴∠BFE=90。,
∴∠A=∠ABC=∠BFE=90。.
∴四边形ABFE是矩形,
∴
AB=EF.
∵S矩形ABCD=AB.BC,
2.如图在矩形ABCD中,对角线AC,BD相交于点O,
∠AOB=60°,AB=1,求AC与AD的长.
O
A
B
C
D
解:∵四边形ABCD是矩形,
∴
AC=BD,
∵∠AOB=60。,
∴
△AOB为等边三角形,
∴
AB=AO=BO=1,
∴
AC=BD=2AO=2.
∵∠BAD=90。,
3.如图,点P是矩形ABCD的边AD上的一个动点,矩形的
两条边长AB、BC分别为8和15.
求点P到矩形的两条对角线AC和BD的距离之和.
(提示:记对角线AC和BD的交点为点O,连结OP)
A
B
C
D
P
.
解:记对角线AC和BD的交点为点O,连结OP.
O
E
F
过点P作PE⊥AC,PF⊥BD,
垂足分别为点E、F,
∵四边形ABCD是矩形,
∴∠ABC=90。,
A
B
C
D
P
.
解:记对角线AC和BD的交点为点O,连结OP.
O
E
F
过点P作PE⊥AC,PF⊥BD,垂足分别为点E、F,
∵四边形ABCD是矩形,
∴∠ABC=90。,
在□ABCD中,∠A=90。,
∴
四边形ABCD是矩形.
课堂小结
一.矩形的定义:
有一个角是直角的平行四边形是矩形.
几何语言:
二.矩形的性质:
矩形的性质定理1
矩形的四个角都是直角.
A
B
C
D
矩形
几何语言:∵
四边形ABCD是矩形,
∴
∠A=∠B=∠C=∠D=90°.
矩形的性质定理2
矩形的对角线互相平分.
几何语言:∵
四边形ABCD是矩形,
∴
AC=BD.
平行四边形、矩形对比理解
对称性
边
角
对角线
平行四边形的一般性性质
矩形的
特殊性质
对边平行
且相等
邻边
垂直
四个角
都是直角
中心对称
图形
既是中心对称图形又是轴对称图形
对角相等
邻角互补
对角线
互相平分
对角线
相等
课堂小结
作业与练习
书面作业:课本P106
习题19.1
1
练习:学习检测
P62-65
1至17
预习任务
预习课本P102-105
19.1.2
矩形的判定
教学反思
作业存在的主要问题
19.1.1
矩形的性质
第19章
矩
形、菱形与正方形
教学目标
教学重点与难点
重点:矩形的性质及其应用.
难点:灵活利用矩形的性质解题.
1.探索并掌握矩形的性质.
2.能灵活运用矩形的性质,进行计算和证明.
3.体会数学的推理和转化思想.
平行四边形
A
B
C
D
四边形
A
B
C
D
AD//BC,DC//AB
一般
特殊
温故夯基
我们知道的平行四边形
作为四边形特殊形式的平行四边形具有哪些特殊性质呢?
1.平行四边形是中心对称图形.
2.平行四边形的对边平行且相等.
(邻边之和等于周长的一半)
3.平行四边形的对角相等.
(邻角互补)
4.平行四边形的对角线互相平分.
问题:如图,用四根木条做一个平行四边形的活动木框,将其直立在地面上并轻轻推动,你会发现什么?
平行四边形的变形
D
A
C
B
D
A
C
B
?
┓
90°
发现
角的大小变了,但不管如何,
它仍然保持平行四边形的形状.
我是平行四边形的特殊形式—矩形!
试一试
A
B
C
D
平行四边形
有一个角是直角
A
B
C
D
矩形
在□ABCD中,∠A=90。,
∴
四边形ABCD是矩形.
学习新知
一.矩形的定义:
有一个角是直角的平行四边形是矩形.
几何语言:
矩形是特殊的平行四边形,特殊在有一个角是直角!
四边形、平行四边形和矩形的关系
四边形
平行四边形
矩形
两组对边分别平行
有一个角是直角
四边形
平行四边形
矩形
作为平行四边形特殊形式的矩形具有哪些性质呢?
二.矩形的性质:
A
B
C
D
平行四边形
有一个角是直角
A
B
C
D
矩形
矩形是特殊的平行四边形,因此平行四边形所具有
的一切性质矩形都具有.即:
(1)矩形是中心对称图形,对称中心是对角线的交点;
(2)矩形对边平行且相等;
(3)矩形的对角相等,邻角互补;
(4)矩形的对角线互相平分.
共性
作为特殊的平行四边形,矩形具有哪些特有性质呢?
是
(2)矩形是中心对称图形吗?若是,对称中心是什么?
B
C
D
A
O
二.矩形的性质:
问题:矩形是特殊的平行四边形,因此矩形除具有平行
四边形的性质外,还有它的特殊性质。你能说出矩形有
哪些特殊性质吗?
(1)矩形是轴对称图形吗?如果是,对称轴是什么?
【结论】矩形既是中心对称图形,又是轴对称图形,
对称中心是对角线的交点,对称轴是经过对边中点的直线.
D
A
C
B
O
D
A
C
B
┓
O
(2)平行四边形的对角线有何关系?矩形的对角线呢?
二.矩形的性质:
观察下列图形的变换,从中你能得到什么感悟?
(1)平行四边形的内角有什么关系?矩形的内角呢?
矩形的四个角都是直角.
矩形的对角线相等.
二.矩形的性质:
矩形的性质定理1
矩形的四个角都是直角.
A
B
C
D
矩形
几何语言:
∵
四边形ABCD是矩形,
∴
∠A=∠B=∠C=∠D=90°.
矩形的性质定理2
矩形的对角线相等.
几何语言:
∵
四边形ABCD是矩形,
∴
AC=BD.
平行四边形、矩形对比理解
对称性
边
角
对角线
平行四边形的一般性性质
矩形的
特殊性质
对边平行
且相等
邻边
垂直
四个角
都是直角
中心对称
图形
既是中心对称图形又是轴对称图形
对角相等
邻角互补
对角线
互相平分
对角线
相等
对比归纳
例1
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,矩形的对角线长
是13cm,那么该矩形的周长是多少?
解:
∵
△AOB、
△BOC、
△COD
和△AOD四个三角形的周长和为86cm,
例题精析
∴
AB+BC+CD+DA+2(OA+OB+OC+OD)
=AB+BC+CD+DA+2(AC+BD)=86.
又∵AC=BD=13cm,
∴
AB+BC+CD+DA=86-2(AC+BD)
=86-4×13
=34(cm),
即矩形ABCD的周长等于34cm.
例2
如图,在矩形ABCD中,点E在边CD上.将该矩形沿AE
折叠,恰好使点D落在边BC上的点F处,如果∠BAF=60°,
求∠DAE的大小.
C
D
B
A
F
E
解:∵四边形ABCD是矩形,
∴
∠BAD=90°.
∵
∠BAF=60°,
∴
∠FAD=30°.
又∵△DAE沿AE折叠得到△FAE,
∴
∠DAE=∠FAE=
=15°.
B
D
随堂练习
1.矩形具有而平行四边行不具有的的性质是(
).
A.
对角相等
B.
对角线相等
C.
对角线互相平分
D.
对边平行且相等
2.矩形的一条对角线与一边的夹角为40°,
则两条对角线相交所成的锐角是(
).
A.
20°
B.
40°
C.
60°
D.
80°
3.在矩形ABCD中,对角线AC,BD交于点O,
下列说法错误的是(
).
A.
AB∥DC
B.
AC=BD
C.
AC⊥BD
D.
OA=OB
C
4.如图,矩形ABCD的顶点A,C分别在直线a,b上,且a//b,∠1=60°,则∠2的度数为(
).
A.
60°
B.
30°
C.
45°
D.
75°
A
B
C
D
a
b
1
2
5.如图,在矩形ABCD中,E为BC边的中点,∠AEC的平分线交AD边于点F,若AB=3,AD=8,则FD的长为(
).
A.
1
B.
2
C.
3
D.
4
D
A
B
C
E
F
A
C
(4)
(5)
6.将长方形ABCD的纸片沿EF折成如图所示,
?EFG=55°,则?FGE=
.
A
D'
C'
F
B
D
C
E
G
70°
7.将矩形ABCD的纸片沿EF折叠后,ED与BC的交点为G,
点D、
C分别落在D'
、C'的位置上,若∠EFG=60°,
则∠1=
,∠2=
.
1
2
A
B
C
D
E
F
C'
D'
G
(6)
(7)
60°
120°
例题精析
例3
如图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,
垂足为点E.试求BE的长.
A
B
C
D
E
┏
解:在矩形ABCD在,∠ABC=90°,
例4
如图,在矩形ABCD中,对角线AC与BD交于点O,
AE垂直且平分线段BO,垂足为点E,BD=15cm.
求AC、AB的长.
∟
A
B
C
D
O
E
解:∵四边形ABCD是矩形,
∴
AC=BD=15,
∵AE垂直平分BO,
∴AB=AO=7.5
.
即AC的长为15cm,AB的长为7.5cm
.
若∠AOD=120。,AB=4,求AC、AD及矩形的面积.
例4
如图,在矩形ABCD中,对角线AC与BD交于点O,
AE垂直且平分线段BO,垂足为点E,BD=15cm.
∟
A
B
C
D
O
E
解:∵四边形ABCD是矩形,
∴
AC=BD,
若∠AOD=120。,AB=4,求AC、AD及矩形的面积.
∵∠AOD=120。,
∴∠AOB=60。,
∴△AOB为等边三角形,
∴
AB=AO=BO=4,
∴
AC=BD=2AO=8.
∵∠BAD=90。,
∴矩形的面积为AB.AD
1.如图,在矩形的ABCD中,E是AD边上一点,
试说明△BCE的面积与矩形ABCD的面积之间的关系.
A
B
C
D
E
随堂练习
┏
F
解:过点E作EF⊥BC于点F,
∵四边形ABCD是矩形,
∴∠A=∠ABC=90。.
∵
EF⊥BC,
∴∠BFE=90。,
∴∠A=∠ABC=∠BFE=90。.
∴四边形ABFE是矩形,
∴
AB=EF.
∵S矩形ABCD=AB.BC,
2.如图在矩形ABCD中,对角线AC,BD相交于点O,
∠AOB=60°,AB=1,求AC与AD的长.
O
A
B
C
D
解:∵四边形ABCD是矩形,
∴
AC=BD,
∵∠AOB=60。,
∴
△AOB为等边三角形,
∴
AB=AO=BO=1,
∴
AC=BD=2AO=2.
∵∠BAD=90。,
3.如图,点P是矩形ABCD的边AD上的一个动点,矩形的
两条边长AB、BC分别为8和15.
求点P到矩形的两条对角线AC和BD的距离之和.
(提示:记对角线AC和BD的交点为点O,连结OP)
A
B
C
D
P
.
解:记对角线AC和BD的交点为点O,连结OP.
O
E
F
过点P作PE⊥AC,PF⊥BD,
垂足分别为点E、F,
∵四边形ABCD是矩形,
∴∠ABC=90。,
A
B
C
D
P
.
解:记对角线AC和BD的交点为点O,连结OP.
O
E
F
过点P作PE⊥AC,PF⊥BD,垂足分别为点E、F,
∵四边形ABCD是矩形,
∴∠ABC=90。,
在□ABCD中,∠A=90。,
∴
四边形ABCD是矩形.
课堂小结
一.矩形的定义:
有一个角是直角的平行四边形是矩形.
几何语言:
二.矩形的性质:
矩形的性质定理1
矩形的四个角都是直角.
A
B
C
D
矩形
几何语言:∵
四边形ABCD是矩形,
∴
∠A=∠B=∠C=∠D=90°.
矩形的性质定理2
矩形的对角线互相平分.
几何语言:∵
四边形ABCD是矩形,
∴
AC=BD.
平行四边形、矩形对比理解
对称性
边
角
对角线
平行四边形的一般性性质
矩形的
特殊性质
对边平行
且相等
邻边
垂直
四个角
都是直角
中心对称
图形
既是中心对称图形又是轴对称图形
对角相等
邻角互补
对角线
互相平分
对角线
相等
课堂小结
作业与练习
书面作业:课本P106
习题19.1
1
练习:学习检测
P62-65
1至17
预习任务
预习课本P102-105
19.1.2
矩形的判定
教学反思
作业存在的主要问题
