2020-2021学年华东师大版八年级数学下册19.2.1 (1)菱形的性质课件(21张ppt)
文档属性
| 名称 | 2020-2021学年华东师大版八年级数学下册19.2.1 (1)菱形的性质课件(21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 00:00:00 | ||
图片预览


文档简介
19.2.1 菱形的性质
教学目标
教学重点与难点
重点:菱形的性质及其应用.
难点:灵活利用菱形的性质解题.
1.探索并掌握菱形的性质.
2.能灵活运用菱形的性质,进行计算和证明.
3.体会数学的推理和转化思想.
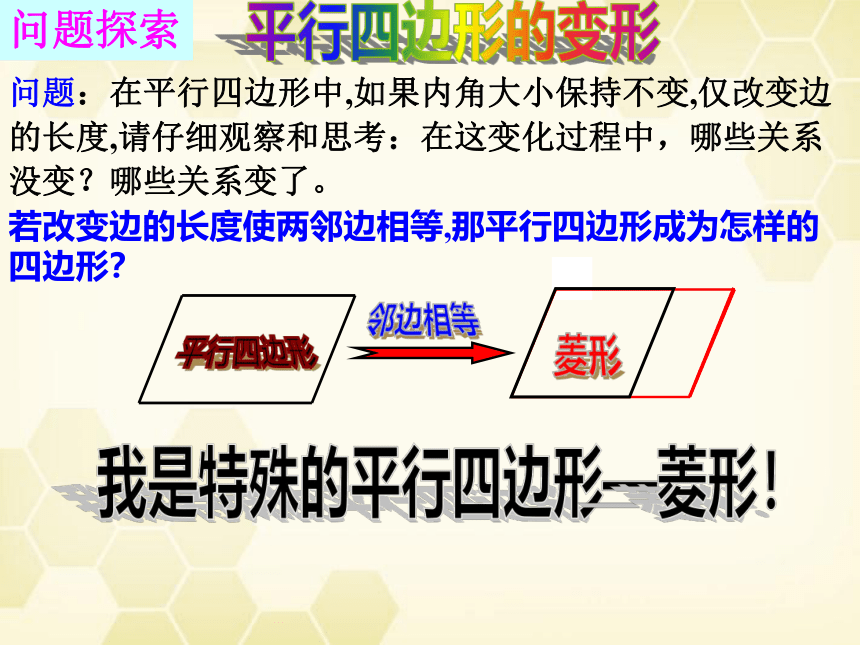
问题:在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考:在这变化过程中,哪些关系没变?哪些关系变了。
问题探索
若改变边的长度使两邻边相等,那平行四边形成为怎样的
四边形?
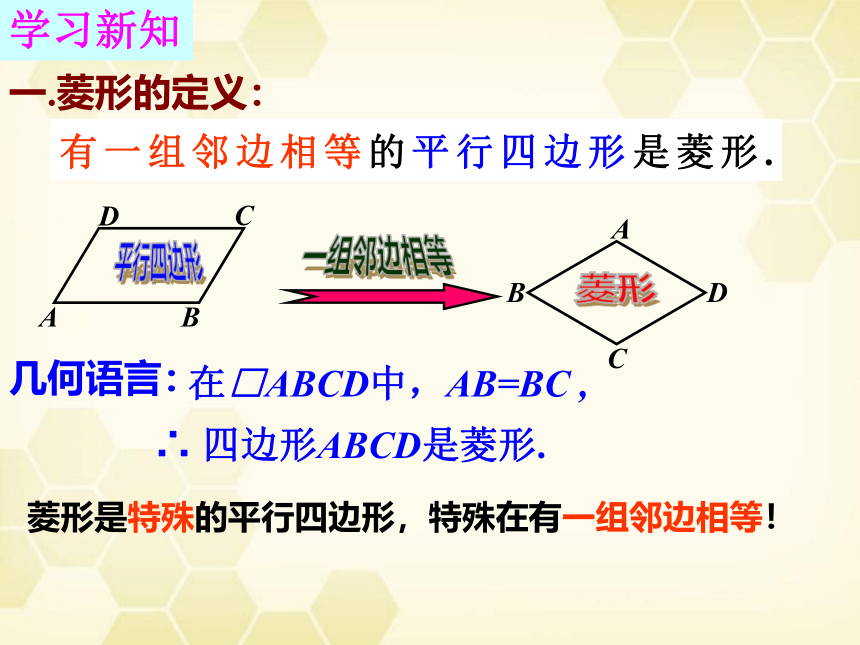
有一组邻边相等的平行四边形是菱形.
A
B
C
D
在□ABCD中,AB=BC ,
∴ 四边形ABCD是菱形.
D
A
B
C
学习新知
一.菱形的定义:
几何语言:
菱形是特殊的平行四边形,特殊在有一组邻边相等!
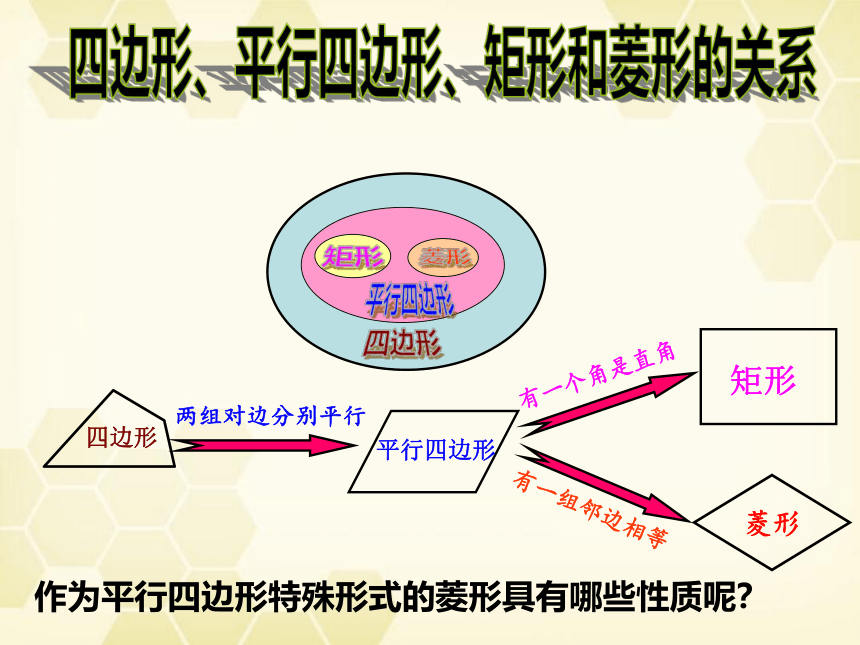
两组对边分别平行
有一个角是直角
四边形
平行四边形
矩形
有一组邻边相等
菱形
作为平行四边形特殊形式的菱形具有哪些性质呢?
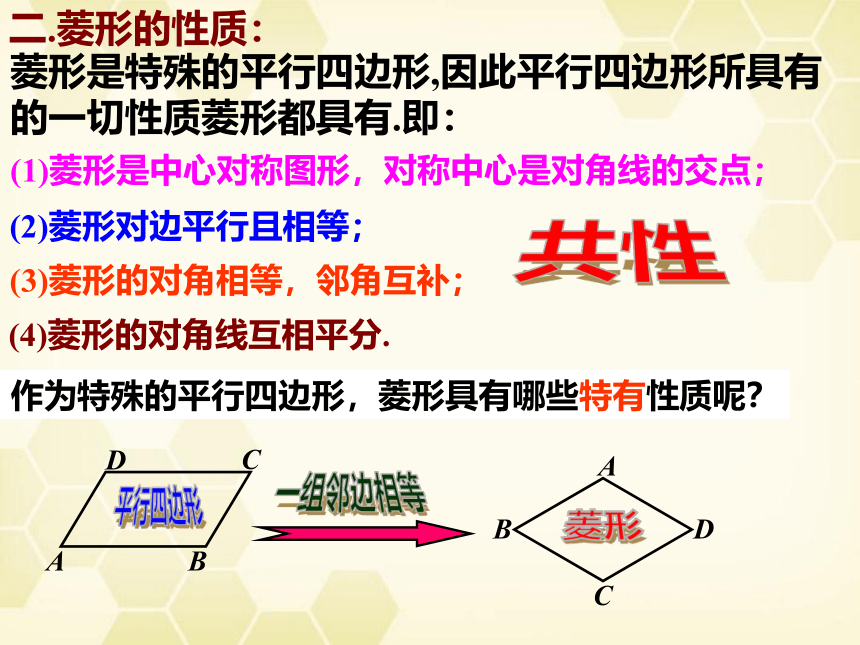
二.菱形的性质:
菱形是特殊的平行四边形,因此平行四边形所具有
的一切性质菱形都具有.即:
(1)菱形是中心对称图形,对称中心是对角线的交点;
(2)菱形对边平行且相等;
(3)菱形的对角相等,邻角互补;
(4)菱形的对角线互相平分.
作为特殊的平行四边形,菱形具有哪些特有性质呢?
A
B
C
D
D
A
B
C
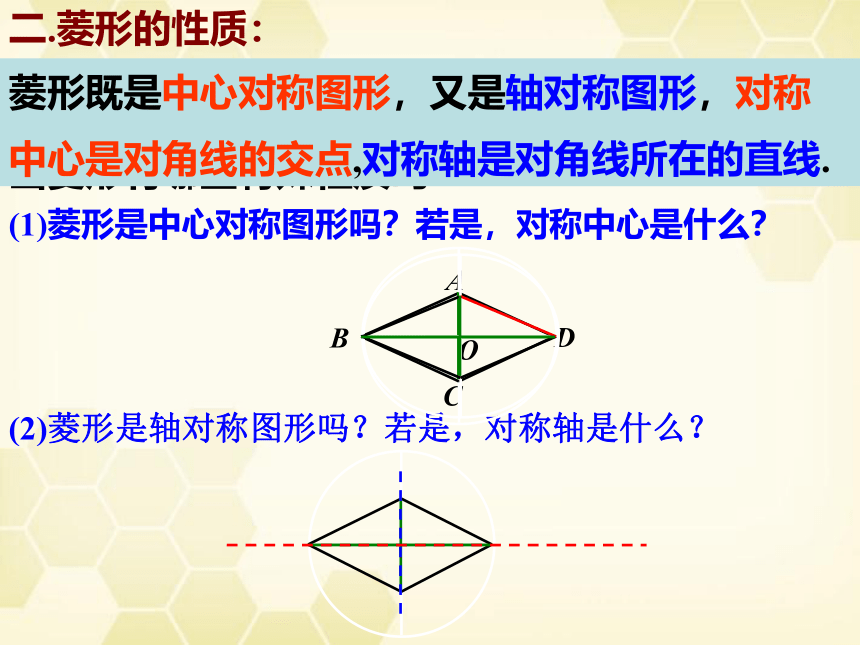
(2)菱形是轴对称图形吗?若是,对称轴是什么?
A
B
C
D
O
二.菱形的性质:
问题:菱形是特殊的平行四边形,因此菱形除具有
平行四边形的性质外,还有它的特殊性质。你能说出菱形有哪些特殊性质吗?
(1)菱形是中心对称图形吗?若是,对称中心是什么?
菱形既是中心对称图形,又是轴对称图形,对称
中心是对角线的交点,对称轴是对角线所在的直线.
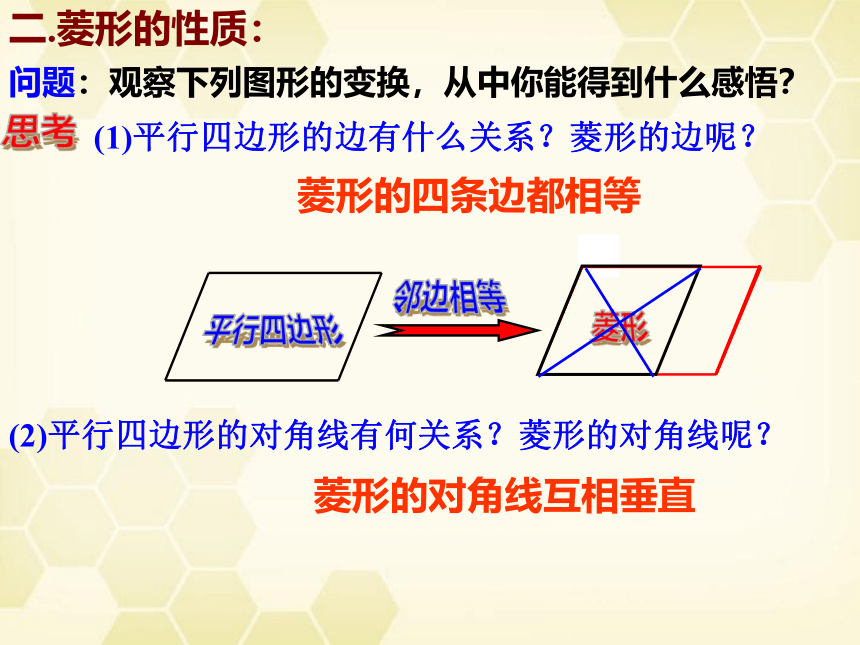
(1)平行四边形的边有什么关系?菱形的边呢?
(2)平行四边形的对角线有何关系?菱形的对角线呢?
二.菱形的性质:
问题:观察下列图形的变换,从中你能得到什么感悟?
菱形的四条边都相等
菱形的对角线互相垂直
二.菱形的性质:
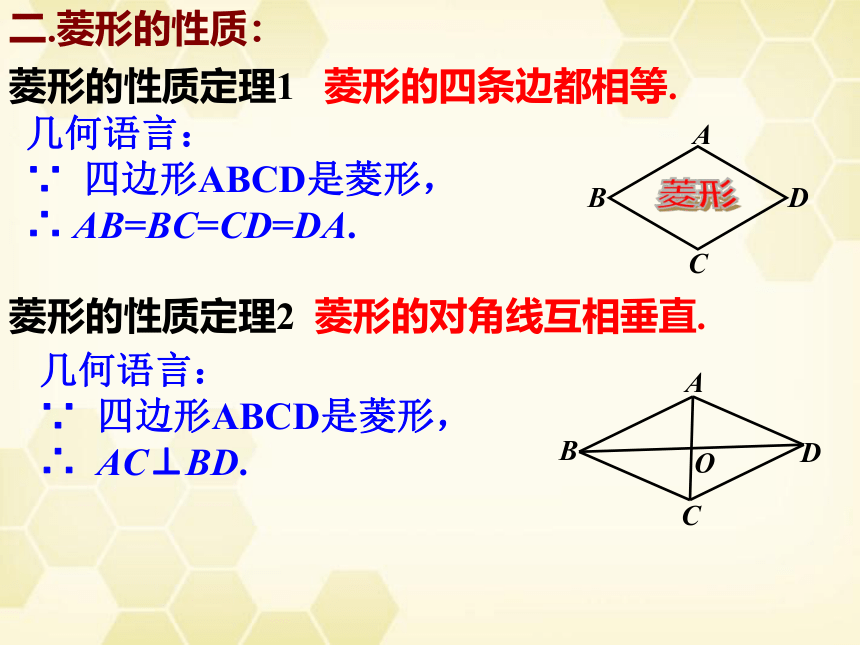
菱形的性质定理1 菱形的四条边都相等.
D
A
B
C
几何语言:
∵ 四边形ABCD是菱形,
∴ AB=BC=CD=DA.
C
B
A
D
O
菱形的性质定理2 菱形的对角线互相垂直.
几何语言:
∵ 四边形ABCD是菱形,
∴ AC⊥BD.
对称性
边
角
对角线
平行四边形的
一般性性质
菱形的
特殊性质
对边平行
且相等
四边都
相等
中心对称
图形
既是中心对称图形又是轴对称图形
对角相等
邻角互补
对角线
互相平分
对角线
互相垂直
对比归纳
问题:菱形是特殊的平行四边形,那么能否利用平行四边形的面积公式计算菱形的面积吗?
C
B
A
D
O
E
能利用对角线求菱形的面积吗?若能,请你计算.
菱形的面积公式:
S菱形 = 底×高=4S△OAB = 对角线乘积的一半.
三.菱形的面积公式:
例1 如图,在菱形ABCD中,∠BAD=2∠B.
(1)求∠B的度数;
(2)试判断△ABC的形状,并说明理由;
(3)若菱形的周长为8cm,求AC、BD的长.
B
C
D
A
O
例题精析
解:(1)在菱形ABCD中,
∵∠B+∠BAD=180°,
∠BAD=2∠B,
∴∠B=60°.
(2)在菱形ABCD中,
∵AB=BC,∠B=60°,
∴△ABC是等边三角形.
(3)∵菱形ABCD的周长为8cm,
∴AB=BC=CD=DA=2cm.
∵△ABC是等边三角形,
∴AC=AB=2cm.
∴AO=1cm.
∵ AC⊥BD,
∴BD=2OB=
解:∵四边形ABCD是菱形,
∴AC⊥BD,
AO= BO= .
∵ AC=6cm,BD=8cm,
∴ AO=3cm,BO=4cm.
在Rt△ABO中,由勾股定理得:
∴菱形的周长=4AB=4×5=20 (cm).
例2 如图,在菱形ABCD中,对角线AC、BD相交于点O,
BD=8cm,AC=6cm,求菱形的周长.
1.菱形具有而一般平行四边形不具有的性质是( ).
A.对边相等 B.对角相等
C.对角线互相平分 D.对角线互相垂直
D
2.菱形和矩形一定都具有的性质是( ).
A.对角线相等 B.对角线互相垂直
C.对角线互相平分且相等 D.对角线互相平分
D
3.如图,菱形ABCD的对角线AC、BD的长分别为10和24,
则这个菱形的周长是( ).
A. 52 B. 40
C. 48 D. 42
A
C
B
A
D
O
随堂练习
4.如图,菱形ABCD中,∠BAD=120°,若△ABC的周长为15,
则菱形ABCD的周长是( ).
A. 25 B. 20 C. 15 D. 10
A
B
C
D
B
5.如图,已知菱形的两条对角线的长分别为6cm和8cm,则这个菱形的高DE为( ).
A. 2.4cm B. 4.8cm C. 5cm D. 9.6cm
B
6.根据下图填一填:
(1)已知菱形ABCD的周长是12cm,那么它的边长是 ______.
(2)在菱形ABCD中,∠ABC=120 °,则∠BAC= _______.
(3)菱形ABCD的两条对角线长分别为6cm和8cm,
则菱形的边长是_______.
3cm
30°
A
B
C
O
D
5cm
(4)菱形的一个内角为120°,平分这个内角的对角线长
为11cm,则菱形的周长为______.
(5)菱形的面积为64 cm2,两条对角线的长度比为1∶2 ,
那么菱形最短的那条对角线长为_______.
44cm
8cm
7.如图,四边形ABCD是边长为13cm的菱形,其中对角线BD
长为10cm.求:(1)对角线AC的长度;(2)菱形ABCD的面积.
解:(1)
∵四边形ABCD是菱形,
∴∠AED=90°,
(2)菱形ABCD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
有一组邻边相等的平行四边形是菱形.
在□ABCD中,AB=BC ,
∴ 四边形ABCD是菱形.
D
A
B
C
一.菱形的定义:
几何语言:
课堂小结
二.菱形的性质:
菱形的性质定理1 菱形的四条边都相等.
几何语言:∵ 四边形ABCD是菱形,
∴ AB=BC=CD=DA.
菱形的性质定理2 菱形的对角线互相垂直.
C
B
A
D
O
几何语言:∵ 四边形ABCD是菱形,
∴ AC⊥BD.
对称性
边
角
对角线
平行四边形的
一般性性质
菱形的
特殊性质
对边平行
且相等
四边都
相等
中心对称
图形
既是中心对称图形又是轴对称图形
对角相等
邻角互补
对角线
互相平分
对角线
互相垂直
课堂小结
作业与练习
书面作业:课本P118 习题19.2 1
练习:学习检测 P67-68 1至16
预习任务
预习课本P112-113 19.2.1 菱形的性质
例2与例3
教学反思
作业存在的主要问题
教学目标
教学重点与难点
重点:菱形的性质及其应用.
难点:灵活利用菱形的性质解题.
1.探索并掌握菱形的性质.
2.能灵活运用菱形的性质,进行计算和证明.
3.体会数学的推理和转化思想.
问题:在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考:在这变化过程中,哪些关系没变?哪些关系变了。
问题探索
若改变边的长度使两邻边相等,那平行四边形成为怎样的
四边形?
有一组邻边相等的平行四边形是菱形.
A
B
C
D
在□ABCD中,AB=BC ,
∴ 四边形ABCD是菱形.
D
A
B
C
学习新知
一.菱形的定义:
几何语言:
菱形是特殊的平行四边形,特殊在有一组邻边相等!
两组对边分别平行
有一个角是直角
四边形
平行四边形
矩形
有一组邻边相等
菱形
作为平行四边形特殊形式的菱形具有哪些性质呢?
二.菱形的性质:
菱形是特殊的平行四边形,因此平行四边形所具有
的一切性质菱形都具有.即:
(1)菱形是中心对称图形,对称中心是对角线的交点;
(2)菱形对边平行且相等;
(3)菱形的对角相等,邻角互补;
(4)菱形的对角线互相平分.
作为特殊的平行四边形,菱形具有哪些特有性质呢?
A
B
C
D
D
A
B
C
(2)菱形是轴对称图形吗?若是,对称轴是什么?
A
B
C
D
O
二.菱形的性质:
问题:菱形是特殊的平行四边形,因此菱形除具有
平行四边形的性质外,还有它的特殊性质。你能说出菱形有哪些特殊性质吗?
(1)菱形是中心对称图形吗?若是,对称中心是什么?
菱形既是中心对称图形,又是轴对称图形,对称
中心是对角线的交点,对称轴是对角线所在的直线.
(1)平行四边形的边有什么关系?菱形的边呢?
(2)平行四边形的对角线有何关系?菱形的对角线呢?
二.菱形的性质:
问题:观察下列图形的变换,从中你能得到什么感悟?
菱形的四条边都相等
菱形的对角线互相垂直
二.菱形的性质:
菱形的性质定理1 菱形的四条边都相等.
D
A
B
C
几何语言:
∵ 四边形ABCD是菱形,
∴ AB=BC=CD=DA.
C
B
A
D
O
菱形的性质定理2 菱形的对角线互相垂直.
几何语言:
∵ 四边形ABCD是菱形,
∴ AC⊥BD.
对称性
边
角
对角线
平行四边形的
一般性性质
菱形的
特殊性质
对边平行
且相等
四边都
相等
中心对称
图形
既是中心对称图形又是轴对称图形
对角相等
邻角互补
对角线
互相平分
对角线
互相垂直
对比归纳
问题:菱形是特殊的平行四边形,那么能否利用平行四边形的面积公式计算菱形的面积吗?
C
B
A
D
O
E
能利用对角线求菱形的面积吗?若能,请你计算.
菱形的面积公式:
S菱形 = 底×高=4S△OAB = 对角线乘积的一半.
三.菱形的面积公式:
例1 如图,在菱形ABCD中,∠BAD=2∠B.
(1)求∠B的度数;
(2)试判断△ABC的形状,并说明理由;
(3)若菱形的周长为8cm,求AC、BD的长.
B
C
D
A
O
例题精析
解:(1)在菱形ABCD中,
∵∠B+∠BAD=180°,
∠BAD=2∠B,
∴∠B=60°.
(2)在菱形ABCD中,
∵AB=BC,∠B=60°,
∴△ABC是等边三角形.
(3)∵菱形ABCD的周长为8cm,
∴AB=BC=CD=DA=2cm.
∵△ABC是等边三角形,
∴AC=AB=2cm.
∴AO=1cm.
∵ AC⊥BD,
∴BD=2OB=
解:∵四边形ABCD是菱形,
∴AC⊥BD,
AO= BO= .
∵ AC=6cm,BD=8cm,
∴ AO=3cm,BO=4cm.
在Rt△ABO中,由勾股定理得:
∴菱形的周长=4AB=4×5=20 (cm).
例2 如图,在菱形ABCD中,对角线AC、BD相交于点O,
BD=8cm,AC=6cm,求菱形的周长.
1.菱形具有而一般平行四边形不具有的性质是( ).
A.对边相等 B.对角相等
C.对角线互相平分 D.对角线互相垂直
D
2.菱形和矩形一定都具有的性质是( ).
A.对角线相等 B.对角线互相垂直
C.对角线互相平分且相等 D.对角线互相平分
D
3.如图,菱形ABCD的对角线AC、BD的长分别为10和24,
则这个菱形的周长是( ).
A. 52 B. 40
C. 48 D. 42
A
C
B
A
D
O
随堂练习
4.如图,菱形ABCD中,∠BAD=120°,若△ABC的周长为15,
则菱形ABCD的周长是( ).
A. 25 B. 20 C. 15 D. 10
A
B
C
D
B
5.如图,已知菱形的两条对角线的长分别为6cm和8cm,则这个菱形的高DE为( ).
A. 2.4cm B. 4.8cm C. 5cm D. 9.6cm
B
6.根据下图填一填:
(1)已知菱形ABCD的周长是12cm,那么它的边长是 ______.
(2)在菱形ABCD中,∠ABC=120 °,则∠BAC= _______.
(3)菱形ABCD的两条对角线长分别为6cm和8cm,
则菱形的边长是_______.
3cm
30°
A
B
C
O
D
5cm
(4)菱形的一个内角为120°,平分这个内角的对角线长
为11cm,则菱形的周长为______.
(5)菱形的面积为64 cm2,两条对角线的长度比为1∶2 ,
那么菱形最短的那条对角线长为_______.
44cm
8cm
7.如图,四边形ABCD是边长为13cm的菱形,其中对角线BD
长为10cm.求:(1)对角线AC的长度;(2)菱形ABCD的面积.
解:(1)
∵四边形ABCD是菱形,
∴∠AED=90°,
(2)菱形ABCD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
有一组邻边相等的平行四边形是菱形.
在□ABCD中,AB=BC ,
∴ 四边形ABCD是菱形.
D
A
B
C
一.菱形的定义:
几何语言:
课堂小结
二.菱形的性质:
菱形的性质定理1 菱形的四条边都相等.
几何语言:∵ 四边形ABCD是菱形,
∴ AB=BC=CD=DA.
菱形的性质定理2 菱形的对角线互相垂直.
C
B
A
D
O
几何语言:∵ 四边形ABCD是菱形,
∴ AC⊥BD.
对称性
边
角
对角线
平行四边形的
一般性性质
菱形的
特殊性质
对边平行
且相等
四边都
相等
中心对称
图形
既是中心对称图形又是轴对称图形
对角相等
邻角互补
对角线
互相平分
对角线
互相垂直
课堂小结
作业与练习
书面作业:课本P118 习题19.2 1
练习:学习检测 P67-68 1至16
预习任务
预习课本P112-113 19.2.1 菱形的性质
例2与例3
教学反思
作业存在的主要问题
