2020-2021学年华东师大版八年级数学下册19.2.2菱形的判定(2)课件(共21张PPT)
文档属性
| 名称 | 2020-2021学年华东师大版八年级数学下册19.2.2菱形的判定(2)课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 632.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 00:00:00 | ||
图片预览


文档简介
(共21张PPT)
19.2.2
菱形的判定
第19章
矩
形、菱形与正方形
教学目标
教学重点与难点
重点:菱形的判定定理及其应用.
难点:灵活利用菱形的判定定理解题.
1.探索并掌握菱形的判定定理.
2.能灵活运用菱形的判定定理解题.
3.体会数学的推理和转化思想.
菱形的判定
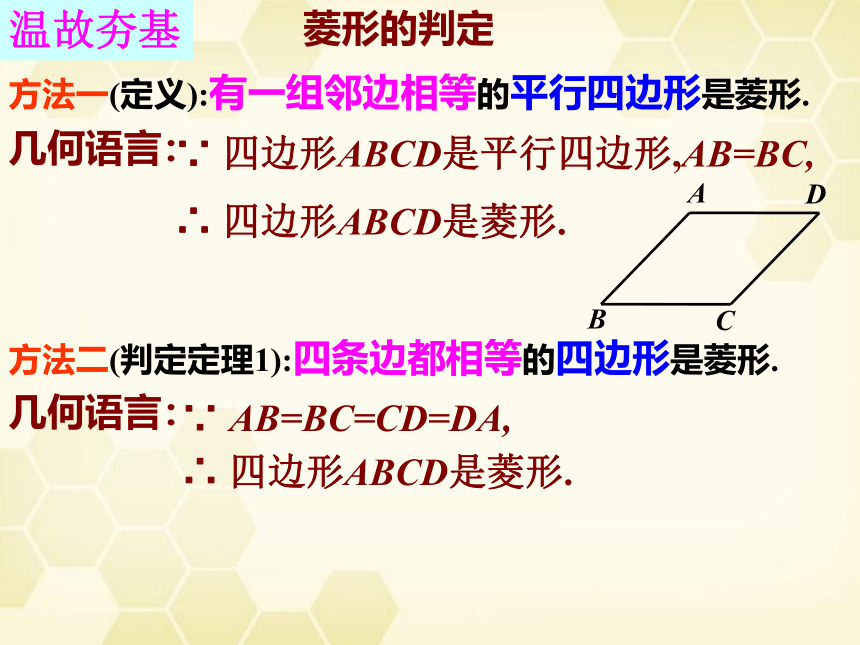
方法一(定义):有一组邻边相等的平行四边形是菱形.
B
A
C
D
几何语言:
∵
四边形ABCD是平行四边形,AB=BC,
∴
四边形ABCD是菱形.
方法二(判定定理1):四条边都相等的四边形是菱形.
几何语言:
∵
AB=BC=CD=DA,
∴
四边形ABCD是菱形.
温故夯基
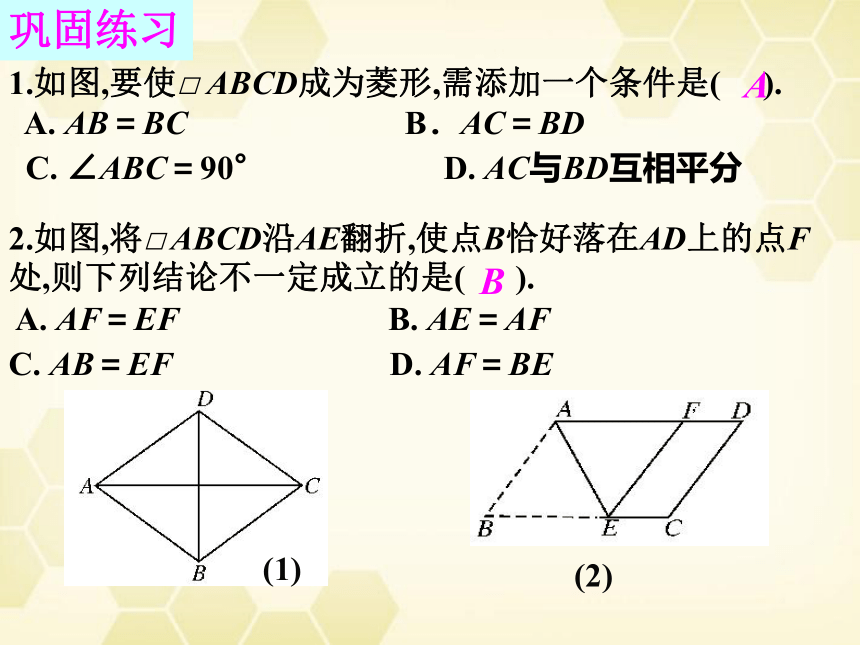
1.如图,要使□
ABCD成为菱形,需添加一个条件是(
).
A.
AB=BC
B.AC=BD
C.
∠ABC=90°
D.
AC与BD互相平分
巩固练习
2.如图,将□
ABCD沿AE翻折,使点B恰好落在AD上的点F
处,则下列结论不一定成立的是(
).
A.
AF=EF
B.
AE=AF
C.
AB=EF
D.
AF=BE
(1)
(2)
A
B
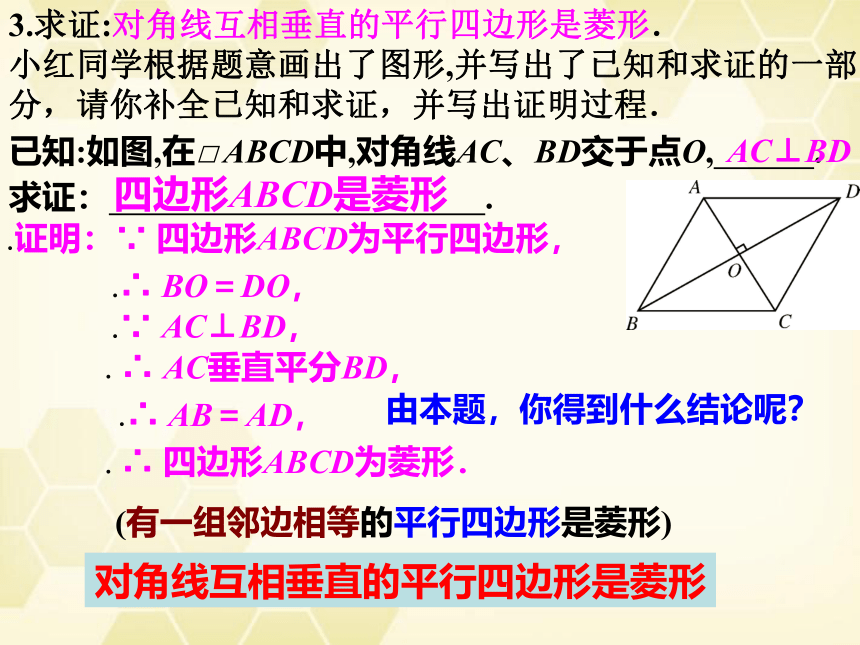
3.求证:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部
分,请你补全已知和求证,并写出证明过程.
已知:如图,在□
ABCD中,对角线AC、BD交于点O,
.
求证:
.
.证明:∵
四边形ABCD为平行四边形,
AC⊥BD
四边形ABCD是菱形
.∴
BO=DO,
.∵
AC⊥BD,
.
∴
AC垂直平分BD,
.∴
AB=AD,
.
∴
四边形ABCD为菱形.
(有一组邻边相等的平行四边形是菱形)
由本题,你得到什么结论呢?
对角线互相垂直的平行四边形是菱形
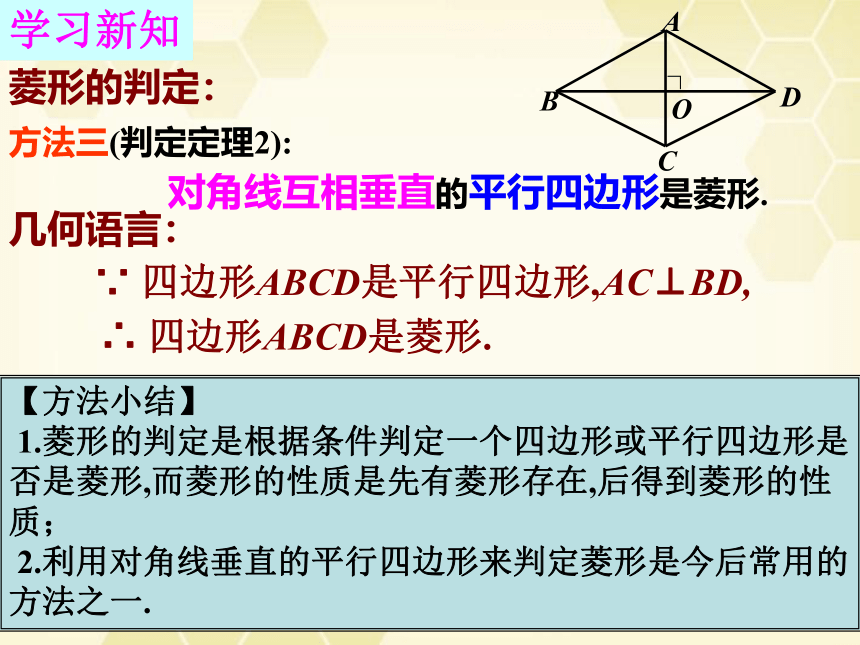
学习新知
菱形的判定:
方法三(判定定理2):
对角线互相垂直的平行四边形是菱形.
几何语言:
∵
四边形ABCD是平行四边形,AC⊥BD,
∴
四边形ABCD是菱形.
A
B
C
D
O
∟
【方法小结】
1.菱形的判定是根据条件判定一个四边形或平行四边形是否是菱形,而菱形的性质是先有菱形存在,后得到菱形的性质;
2.利用对角线垂直的平行四边形来判定菱形是今后常用的方法之一.
菱形的判定
方法一(定义):有一组邻边相等的平行四边形是菱形.
B
A
C
D
几何语言:∵
四边形ABCD是平行四边形,AB=BC,
∴
四边形ABCD是菱形.
方法二(判定定理1):四条边都相等的四边形是菱形.
几何语言:∵
AB=BC=CD=DA,
∴
四边形ABCD是菱形.
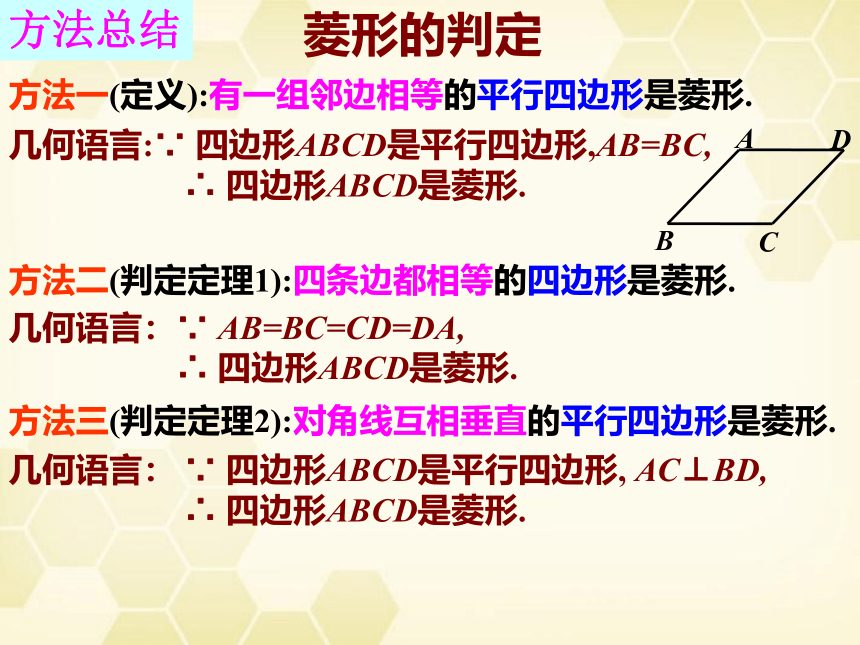
方法总结
方法三(判定定理2):对角线互相垂直的平行四边形是菱形.
几何语言:
∵
四边形ABCD是平行四边形,
AC⊥BD,
∴
四边形ABCD是菱形.
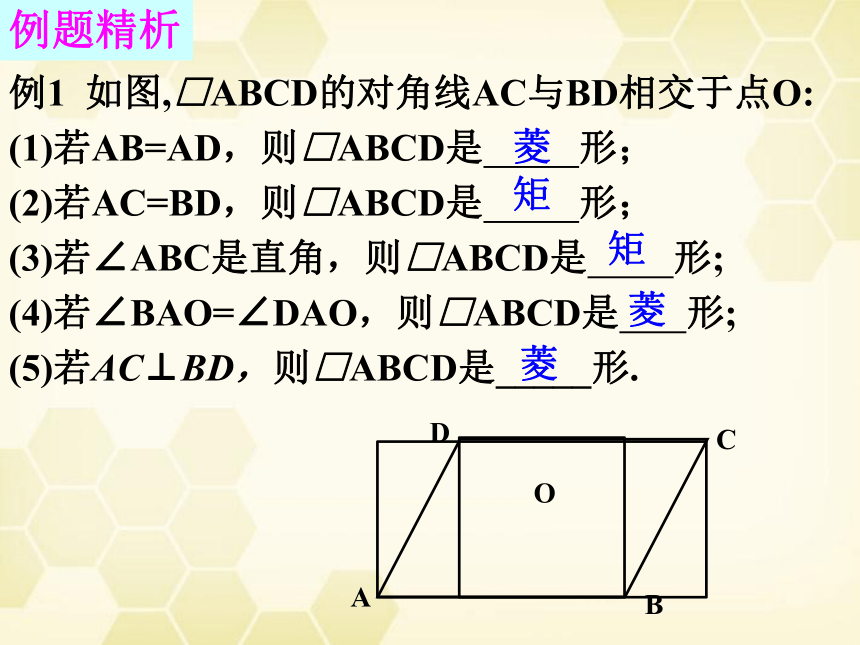
例1
如图,□ABCD的对角线AC与BD相交于点O:
(1)若AB=AD,则□ABCD是
形;
(2)若AC=BD,则□ABCD是
形;
(3)若∠ABC是直角,则□ABCD是
形;
(4)若∠BAO=∠DAO,则□ABCD是
形;
(5)若AC⊥BD,则□ABCD是_____形.
A
B
C
D
O
矩
菱
矩
菱
例题精析
菱
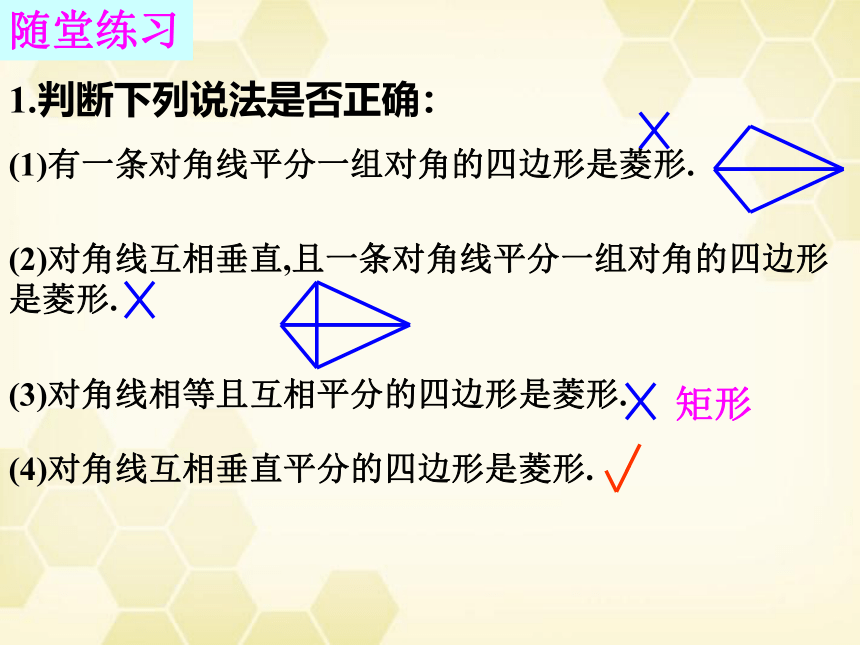
(1)有一条对角线平分一组对角的四边形是菱形.
(3)对角线相等且互相平分的四边形是菱形.
矩形
(2)对角线互相垂直,且一条对角线平分一组对角的四边形是菱形.
(4)对角线互相垂直平分的四边形是菱形.
随堂练习
1.判断下列说法是否正确:
2.如图,已知四边形ABCD是平行四边形,要使它成为
菱形,那么需要添加的条件可以是(
).
A.AC⊥BD
B.AB=AC
C.∠ABC=90°
D.AC=BD
A
3.如图,在□
ABCD中,AC平分∠DAB,AB=2,
则□
ABCD的周长为(
).
A.4
B.6
C.8
D.12
C
4.如图所示,下列条件中能说明四边形ABCD
是菱形的有(
).
①BD⊥AC;
②OA=OC,OB=OD,AB=BC;
③AC=BD;
④AB=BC,AB∥CD.
A.
①
B.
②
C.
①②
D.③④
A
B
C
D
O
B
6.
平行四边形ABCD的对角线AC平分∠BAD,
则平行四边形ABCD____(填“是”或“不是”)菱形.
7.
四边形ABCD是平行四边形,请补充一个条件:________,使它是菱形.
是
AB=BC
AC⊥BD
5.下列条件中,不能判定四边形ABCD是菱形的是(
).
A.
AC⊥BD,AC与BD互相平分
B.
AB=BC=CD=DA
C.
AB=BC,AD=CD,AC⊥BD
D.AB=CD,AD=BC,AC⊥BD
C
A
D
E
C
F
B
O
1
2
例题精析
例2
如图,已知矩形ABCD的对角线AC的垂直平分线与
边AD、BC分别交于点E、F.求证:四边形AFCE是菱形.
分析:
要证四边形AFCE是菱形,
由已知条件可知EF⊥AC,
所以只需证明四边形AFCE
是平行四边形,
又知EF垂直平分AC,
因此只需证OE=OF.
A
D
E
C
F
B
O
1
2
例题精析
例2
如图,已知矩形ABCD的对角线AC的垂直平分线与
边AD、BC分别交于点E、F.求证:四边形AFCE是菱形.
证明:∵四边形ABCD是矩形,
∴
AE∥FC,
∴∠1=∠2.
∵EF平分AC,
∴OA=OC.
又∵∠AOE=∠COF=90°,
∴
△AOE≌△COF,
∴OE=OF,
∴
四边形AFCE是平行四边形.
又∵EF⊥AC,
∴四边形AFCE是菱形.
(对角线互相垂直的平行四边形
是菱形)
例3
如图,在□ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.
(1)求证:四边形AECF是菱形;
(2)若∠BAC=90°,AB=6,AC=8,求四边形AECF的面积.
E
A
B
C
D
F
(1)证明:∵四边形ABCD是平行四边形,
∴
AD=
BC,
AD∥BC.
∵
DE=BF,
∴
AE=
FC,AE∥FC,
∴
四边形AECF是平行四边形.
又∵AC⊥EF,
∴四边形AECF是菱形.
(对角线互相垂直的平行四边形是菱形)
例3
如图,在□ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.
(1)求证:四边形AECF是菱形;
(2)若∠BAC=90°,AB=6,AC=8,求四边形AECF的面积.
E
A
B
C
D
F
(2)
∵∠BAC=90°,AB=6,AC=8,
∴
AB⊥EF.
又∵AC⊥EF,
∴
AB∥EF.
∵
AD∥BC,
∴
四边形ABFE是平行四边形,
∴
EF=AB=
6.
∵四边形AECF是菱形,
∴四边形AECF的面积为
1.如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB,AC于点E,F.连结DE,DF.
求证:四边形AEDF是菱形.
D
A
E
F
B
C
随堂练习
证明:∵AD平分∠BAC,∴
∠BAD=∠CAD.
又∵EF⊥AD,∴∠AOE=∠AOF=90°.
在△AEO和△AFO中,
∵∠EAO=∠FAO,AO=AO,∠AOE=∠AOF
∴△AEO≌△AFO,
∴EO=FO.
又∵A点与D点重合,∴AO=DO,
∴EF、AD相互平分,
∴四边形AEDF是平行四边形.
又EF⊥AD,
∴平行四边形AEDF为菱形.
O
A
B
C
D
E
F
G
H
O
证明:∵四边形ABCD是平行四边形,
∴
OD=OB,OA=OC,AD//CB,
∴∠OBG=∠ODE.
又∵∠BOG=∠DOE,
∴△OBG≌△ODE,
∴OE=OG.
同理可证:OF=OH.
∴四边形EFGH是平行四边形.
∵EG⊥FH,
∴四边形EFGH是菱形.
2.如图,过□
ABCD的对角线的交点O,作互相垂直的两条直
线EG、FH,与□
ABCD各边分别相交于点E、F、G、H.
求证:四边形EFGH是菱形.
A
B
C
D
P
E
F
解:
□
ABCD是菱形.
理由如下:
∵四边形ABCD是平行四边形,
∴
DC//AB,
∴∠DCA=∠CAB.
∵
PE⊥AB,PF⊥AD,且PE=PF,
∴
∠DAC=∠CAB,
∴∠DAC=∠DCA
,
∴
AD
=DC
,
∴平行四边形ABCD是菱形.
3.如图,在□
ABCD中,点P是对角线AC上的一点,PE⊥AB,
PF⊥AD,垂足分别为点E、F,且PE=PF,□
ABCD是菱形
吗?为什么?
菱形的判定
方法一(定义):有一组邻边相等的平行四边形是菱形.
B
A
C
D
几何语言:∵
四边形ABCD是平行四边形,AB=BC,
∴
四边形ABCD是菱形.
方法二(判定定理1):四条边都相等的四边形是菱形.
几何语言:∵
AB=BC=CD=DA,
∴
四边形ABCD是菱形.
方法三(判定定理2):对角线互相垂直的平行四边形是菱形.
几何语言:
∵
四边形ABCD是平行四边形,
AC⊥BD,
∴
四边形ABCD是菱形.
课堂小结
作业与练习
书面作业:课本P118
习题19.2
3,4
练习:学习检测
P69-70
1至14
预习任务
预习课本P119-120
19.3
正方形
教学反思
作业存在的主要问题
19.2.2
菱形的判定
第19章
矩
形、菱形与正方形
教学目标
教学重点与难点
重点:菱形的判定定理及其应用.
难点:灵活利用菱形的判定定理解题.
1.探索并掌握菱形的判定定理.
2.能灵活运用菱形的判定定理解题.
3.体会数学的推理和转化思想.
菱形的判定
方法一(定义):有一组邻边相等的平行四边形是菱形.
B
A
C
D
几何语言:
∵
四边形ABCD是平行四边形,AB=BC,
∴
四边形ABCD是菱形.
方法二(判定定理1):四条边都相等的四边形是菱形.
几何语言:
∵
AB=BC=CD=DA,
∴
四边形ABCD是菱形.
温故夯基
1.如图,要使□
ABCD成为菱形,需添加一个条件是(
).
A.
AB=BC
B.AC=BD
C.
∠ABC=90°
D.
AC与BD互相平分
巩固练习
2.如图,将□
ABCD沿AE翻折,使点B恰好落在AD上的点F
处,则下列结论不一定成立的是(
).
A.
AF=EF
B.
AE=AF
C.
AB=EF
D.
AF=BE
(1)
(2)
A
B
3.求证:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部
分,请你补全已知和求证,并写出证明过程.
已知:如图,在□
ABCD中,对角线AC、BD交于点O,
.
求证:
.
.证明:∵
四边形ABCD为平行四边形,
AC⊥BD
四边形ABCD是菱形
.∴
BO=DO,
.∵
AC⊥BD,
.
∴
AC垂直平分BD,
.∴
AB=AD,
.
∴
四边形ABCD为菱形.
(有一组邻边相等的平行四边形是菱形)
由本题,你得到什么结论呢?
对角线互相垂直的平行四边形是菱形
学习新知
菱形的判定:
方法三(判定定理2):
对角线互相垂直的平行四边形是菱形.
几何语言:
∵
四边形ABCD是平行四边形,AC⊥BD,
∴
四边形ABCD是菱形.
A
B
C
D
O
∟
【方法小结】
1.菱形的判定是根据条件判定一个四边形或平行四边形是否是菱形,而菱形的性质是先有菱形存在,后得到菱形的性质;
2.利用对角线垂直的平行四边形来判定菱形是今后常用的方法之一.
菱形的判定
方法一(定义):有一组邻边相等的平行四边形是菱形.
B
A
C
D
几何语言:∵
四边形ABCD是平行四边形,AB=BC,
∴
四边形ABCD是菱形.
方法二(判定定理1):四条边都相等的四边形是菱形.
几何语言:∵
AB=BC=CD=DA,
∴
四边形ABCD是菱形.
方法总结
方法三(判定定理2):对角线互相垂直的平行四边形是菱形.
几何语言:
∵
四边形ABCD是平行四边形,
AC⊥BD,
∴
四边形ABCD是菱形.
例1
如图,□ABCD的对角线AC与BD相交于点O:
(1)若AB=AD,则□ABCD是
形;
(2)若AC=BD,则□ABCD是
形;
(3)若∠ABC是直角,则□ABCD是
形;
(4)若∠BAO=∠DAO,则□ABCD是
形;
(5)若AC⊥BD,则□ABCD是_____形.
A
B
C
D
O
矩
菱
矩
菱
例题精析
菱
(1)有一条对角线平分一组对角的四边形是菱形.
(3)对角线相等且互相平分的四边形是菱形.
矩形
(2)对角线互相垂直,且一条对角线平分一组对角的四边形是菱形.
(4)对角线互相垂直平分的四边形是菱形.
随堂练习
1.判断下列说法是否正确:
2.如图,已知四边形ABCD是平行四边形,要使它成为
菱形,那么需要添加的条件可以是(
).
A.AC⊥BD
B.AB=AC
C.∠ABC=90°
D.AC=BD
A
3.如图,在□
ABCD中,AC平分∠DAB,AB=2,
则□
ABCD的周长为(
).
A.4
B.6
C.8
D.12
C
4.如图所示,下列条件中能说明四边形ABCD
是菱形的有(
).
①BD⊥AC;
②OA=OC,OB=OD,AB=BC;
③AC=BD;
④AB=BC,AB∥CD.
A.
①
B.
②
C.
①②
D.③④
A
B
C
D
O
B
6.
平行四边形ABCD的对角线AC平分∠BAD,
则平行四边形ABCD____(填“是”或“不是”)菱形.
7.
四边形ABCD是平行四边形,请补充一个条件:________,使它是菱形.
是
AB=BC
AC⊥BD
5.下列条件中,不能判定四边形ABCD是菱形的是(
).
A.
AC⊥BD,AC与BD互相平分
B.
AB=BC=CD=DA
C.
AB=BC,AD=CD,AC⊥BD
D.AB=CD,AD=BC,AC⊥BD
C
A
D
E
C
F
B
O
1
2
例题精析
例2
如图,已知矩形ABCD的对角线AC的垂直平分线与
边AD、BC分别交于点E、F.求证:四边形AFCE是菱形.
分析:
要证四边形AFCE是菱形,
由已知条件可知EF⊥AC,
所以只需证明四边形AFCE
是平行四边形,
又知EF垂直平分AC,
因此只需证OE=OF.
A
D
E
C
F
B
O
1
2
例题精析
例2
如图,已知矩形ABCD的对角线AC的垂直平分线与
边AD、BC分别交于点E、F.求证:四边形AFCE是菱形.
证明:∵四边形ABCD是矩形,
∴
AE∥FC,
∴∠1=∠2.
∵EF平分AC,
∴OA=OC.
又∵∠AOE=∠COF=90°,
∴
△AOE≌△COF,
∴OE=OF,
∴
四边形AFCE是平行四边形.
又∵EF⊥AC,
∴四边形AFCE是菱形.
(对角线互相垂直的平行四边形
是菱形)
例3
如图,在□ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.
(1)求证:四边形AECF是菱形;
(2)若∠BAC=90°,AB=6,AC=8,求四边形AECF的面积.
E
A
B
C
D
F
(1)证明:∵四边形ABCD是平行四边形,
∴
AD=
BC,
AD∥BC.
∵
DE=BF,
∴
AE=
FC,AE∥FC,
∴
四边形AECF是平行四边形.
又∵AC⊥EF,
∴四边形AECF是菱形.
(对角线互相垂直的平行四边形是菱形)
例3
如图,在□ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.
(1)求证:四边形AECF是菱形;
(2)若∠BAC=90°,AB=6,AC=8,求四边形AECF的面积.
E
A
B
C
D
F
(2)
∵∠BAC=90°,AB=6,AC=8,
∴
AB⊥EF.
又∵AC⊥EF,
∴
AB∥EF.
∵
AD∥BC,
∴
四边形ABFE是平行四边形,
∴
EF=AB=
6.
∵四边形AECF是菱形,
∴四边形AECF的面积为
1.如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB,AC于点E,F.连结DE,DF.
求证:四边形AEDF是菱形.
D
A
E
F
B
C
随堂练习
证明:∵AD平分∠BAC,∴
∠BAD=∠CAD.
又∵EF⊥AD,∴∠AOE=∠AOF=90°.
在△AEO和△AFO中,
∵∠EAO=∠FAO,AO=AO,∠AOE=∠AOF
∴△AEO≌△AFO,
∴EO=FO.
又∵A点与D点重合,∴AO=DO,
∴EF、AD相互平分,
∴四边形AEDF是平行四边形.
又EF⊥AD,
∴平行四边形AEDF为菱形.
O
A
B
C
D
E
F
G
H
O
证明:∵四边形ABCD是平行四边形,
∴
OD=OB,OA=OC,AD//CB,
∴∠OBG=∠ODE.
又∵∠BOG=∠DOE,
∴△OBG≌△ODE,
∴OE=OG.
同理可证:OF=OH.
∴四边形EFGH是平行四边形.
∵EG⊥FH,
∴四边形EFGH是菱形.
2.如图,过□
ABCD的对角线的交点O,作互相垂直的两条直
线EG、FH,与□
ABCD各边分别相交于点E、F、G、H.
求证:四边形EFGH是菱形.
A
B
C
D
P
E
F
解:
□
ABCD是菱形.
理由如下:
∵四边形ABCD是平行四边形,
∴
DC//AB,
∴∠DCA=∠CAB.
∵
PE⊥AB,PF⊥AD,且PE=PF,
∴
∠DAC=∠CAB,
∴∠DAC=∠DCA
,
∴
AD
=DC
,
∴平行四边形ABCD是菱形.
3.如图,在□
ABCD中,点P是对角线AC上的一点,PE⊥AB,
PF⊥AD,垂足分别为点E、F,且PE=PF,□
ABCD是菱形
吗?为什么?
菱形的判定
方法一(定义):有一组邻边相等的平行四边形是菱形.
B
A
C
D
几何语言:∵
四边形ABCD是平行四边形,AB=BC,
∴
四边形ABCD是菱形.
方法二(判定定理1):四条边都相等的四边形是菱形.
几何语言:∵
AB=BC=CD=DA,
∴
四边形ABCD是菱形.
方法三(判定定理2):对角线互相垂直的平行四边形是菱形.
几何语言:
∵
四边形ABCD是平行四边形,
AC⊥BD,
∴
四边形ABCD是菱形.
课堂小结
作业与练习
书面作业:课本P118
习题19.2
3,4
练习:学习检测
P69-70
1至14
预习任务
预习课本P119-120
19.3
正方形
教学反思
作业存在的主要问题
