20.1.3加权平均数的意义-2020-2021学年华东师大版八年级数学下册课件(22张)
文档属性
| 名称 | 20.1.3加权平均数的意义-2020-2021学年华东师大版八年级数学下册课件(22张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 15:51:03 | ||
图片预览








文档简介
(共22张PPT)
20.1.3
加权平均数
第20章
数据的整理与初步处理
教学目标
教学重点与难点
重点:加权平均数的概念及其求法.
难点:用加权平均数解决实际问题.
1.理解和掌握加权平均数的概念.
2.会用加权平均数解决实际生活中的问题.
平均数的概念:
一组数据的总和与这组数据的个数之比叫做这组数据的平均数.
(或算术平均数)
公式表示:
设有一组数据x1,x2,
x3,···
,
xn,
则该组数据的平均数为:
说明:
(1)平均数是体现这组数据的平均水平;
(2)一组数据的平均数有且只有一个.
温故夯基
巩固练习
1.如果一组数据85,80,x,90的平均数是85,则x=____.
2.某学生在一次考试中,语文、数学、英语三门学科的平均分为80分,物理、政治两科的平均分为85,则该生这5门学科的平均分为____.
3.某班共有50名学生,平均身高为168cm,其中30名男生的平均身高为170cm,则20名女生的平均身高为________.
85
82
165
cm
4.在某捐款活动中,九年级某班的同学捐出了自己的零花钱
.现将同学们的捐款数整理成统计表,则该班同学平均每人捐款
元.
捐款数(元)
5
10
20
50
人数
4
17
6
13
24
在日常生活中,我们经常会与平均数打交道,但有时发现以前计算平均数的方法并不适用.
学习新知
(1)商店里有两种苹果,一种单价为
3.50
元/千克,另一种单价为
6
元/千克.小明妈妈买了单价为
3.50
元/千克的苹果
1
千克,单价为
6
元/千克的苹果
3
千克,那么小明妈妈所买苹果的平均价格是两个单价相加除以
2
吗?为什么?
不是
既然不是,你会怎么计算
所买苹果的平均价格呢?
(2)老师在计算学生每学期的总评成绩时,并不是简单地将一个学生的平时成绩与考试成绩相加除以2,而是按照“平时成绩占
40%,考试成绩占
60%”的比例计算(如图),其中考试成绩更为重要.
如果一个学生的平时成绩为
70
分,考试成绩为
90
分,那么他的学期总评成绩是多少?
70
×
40%
+
90
×
60%
=
82(分)
权重
考试60%
平时40%
解:该学生的学期总评成绩是:
加权平均数
考试60%
平时40%
一般来说,由于各个指标在总结果中占有不同的重要性,因而会被赋予不同的权重.
各个指标在总结果中所占的
百分比称为每个指标的权重.
各个指标乘以相应的权重后的和叫做加权平均数.
定义:一般地,如果n个数据中,
x1出现了f1次,
x2出现了f2次,
……,xk出现了fk次(f1+f2+…+fk=n),那么我们把
叫做这n个数的加权平均数.
权重
加权平均数
权重
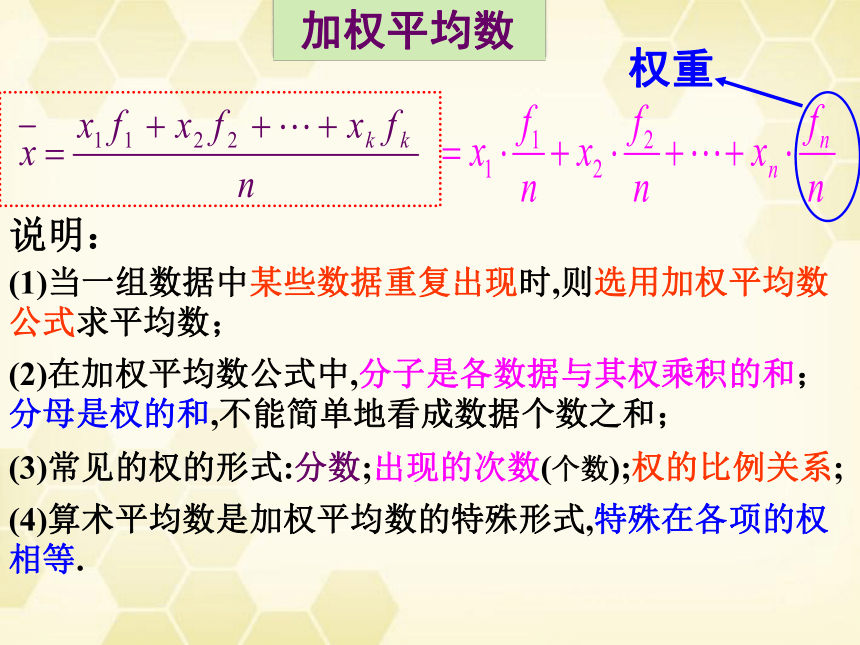
说明:
(1)当一组数据中某些数据重复出现时,则选用加权平均数
公式求平均数;
(2)在加权平均数公式中,分子是各数据与其权乘积的和;
分母是权的和,不能简单地看成数据个数之和;
(3)常见的权的形式:分数;出现的次数(个数);权的比例关系;
(4)算术平均数是加权平均数的特殊形式,特殊在各项的权
相等.
小青七年级第二学期的数学成绩分别为:测验一得
89分,测验二得
78分,测验三得
85分,期中考试得
90分,期末考试得
87分.如果按照图中所显示的平时、期中、期末成绩的权重,那么小青该学期的总评成绩是多少?
期末60%
平时10%
期中30%
试一试
解:小青的平时平均成绩为
89
+
78
+
85
3
=
84,
∴
小青该学期的总评成绩为
84
×
10%
+
90×30%
+
87
×
60%
=
87.6
.
=
8.4+27+52.2
1.某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是(
).
A.
80分
B.
82分
C.
84分
D.
86分
D
随堂练习
3.某学习小组共有学生5人,在一次数学测验中,有2人得85分,2人得90分,1人得70分,该学习小组的平均分是
分.
84
2.某次军训打靶,有a次每次中靶x环,有b次每次中靶y环,
则这个人平均每次中靶的环数是(
).
B
4.在实施清洁工作的过程中,某校对各个班级教室卫生
情况的考评包括以下几项:黑板、门窗、桌椅、地面。
一天,两个班级的各项卫生成绩(单位:分)分别如下表:
黑板
门窗
桌椅
地面
一班
95
85
89
91
二班
90
95
85
90
班级
成绩
项目
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这四项得分依次按15%,10%,35%,40%
的比例计算各班的卫生成绩,那么哪个班的卫生成绩高?请说明理由.
(1)两个班的平均得分分别是多少?
解:(1)一班的平均得分是(95+85+89+91)÷4
=90,
二班的平均得分是(90+95+85+90)÷4
=90.
黑板
门窗
桌椅
地面
一班
95
85
89
91
二班
90
95
85
90
班级
成绩
项目
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这四项得分依次按15%,10%,35%,40%
的比例计算各班的卫生成绩,那么哪个班的卫生成绩高?请说明理由.
(2)一班的加权平均成绩是
95×15%+85×10%+89×35%+91×40%
=14.25+8.5+31.15+36.4
=90,
二班的加权平均成绩是
90×15%+95×10%+85×35%+90×40%
=13.5+9.5+29.75+36
=88.75,
∴一班的卫生成绩高.
某公司对应聘者
A、B、C、D
进行面试,并按三个方面给应聘者打分,每个方面满分20
分,最后打分结果如表所示.如果你是人事主管,会录用哪一位应聘者?
A
B
C
D
专业知识
14
18
17
16
工作经验
18
16
14
16
仪表形象
12
11
14
14
问题探索
总分得分
44
45
45
46
对上述问题,甲同学说:看谁的总分高就录用谁.
通过计算可以发现
D
的总分最高,应该被录用.
这时乙同学说:我有不同意见.三个方面满分都是
20
分,但按理这三个方面的重要性应该有所不同,比如专业知识就应该比仪表形象更重要.
你认为谁的说法比较合理?
乙更合理
假设上述三个方面的重要性之比为
6:3:1,如图所示,那么应该录用谁呢?
专业知识
工作经验
仪表形象
因为
6:3:1
=
60%:30%:10%,
问题探索
所以专业知识、工作经验与仪表形象这三个方面的权重分别是
60%、30%
与
10%.
∵A最后得分为14×60%
+
18×30%
+
12×10%
=
15,
B最后得分为18×60%
+
16×30%
+
11×10%
=
16.7,
C最后得分为17×60%
+
14×30%
+
14×10%
=
15.8,
D最后得分为16×60%
+
16×30%
+
14×10%
=
15.8,
∴
应该录用B.
如果这三个方面的重要性之比为
10:7:3,此时三个方面的权重各是多少?哪一位应该被录用?
A
B
C
D
专业知识
14
18
17
16
工作经验
18
16
14
16
仪表形象
12
11
14
14
10:7:
3
=
50%:35%:15%
问题探索
∵A最后得分为14×50%
+
18×35%
+
12×15%
=
15.1,
B最后得分为18×50%
+
16×35%
+
11×15%
=
16.25,
C最后得分为17×50%
+
14×35%
+
14×15%
=
15.5,
D最后得分为16×50%
+
16×35%
+
14×15%
=
15.7,
∴
应该录用B.
随堂练习
1.
一家小吃店原有三个品种的馄饨,其中菜馅馄饨的售价
为3元/碗,鸡蛋馅馄饨的售价为4元/碗,肉馅馄饨的售价
为5元/碗.每碗均有10个馄饨.该店老板准备推出混合馄饨,
请帮她解决以下问题:
课本P136
3
(1)如果每碗有3个菜馅的、3个鸡蛋馅的、4个肉馅的馄饨,
那么混合馄饨每碗的定价应是多少?
∵菜馅,鸡蛋馅,肉馅单个馄饨价分别为0.3元,0.4元,0.5元,
∴
混合馄饨每碗的定价为:0.3×3+0.4×3+0.5×4=4.1(元).
(2)如果菜馅、鸡蛋馅、肉馅馄饨的个数之比为3∶2∶5,
那么混合馄饨的每碗定价应是多少?
∵菜馅,鸡蛋馅,肉馅单个馄饨价分别为0.3元,0.4元,0.5元,
∴
混合馄饨每碗的定价为:0.3×3+0.4×2+0.5×5=4.2(元).
随堂练习
1.
一家小吃店原有三个品种的馄饨,其中菜馅馄饨的售价
为3元/碗,鸡蛋馅馄饨的售价为4元/碗,肉馅馄饨的售价
为5元/碗.每碗均有10个馄饨.该店老板准备推出混合馄饨,
请帮她解决以下问题:
课本P136
3
∵菜馅,鸡蛋馅,肉馅单个馄饨价分别为0.3元,0.4元,0.5元,
∴
混合馄饨每碗的定价为:0.3×2+0.4×2+0.5×6=4.4(元).
(3)如果菜馅、鸡蛋馅、肉馅馄饨的个数之比为1∶1∶3,
那么混合馄饨的每碗定价应是多少?
(4)如果混合馄饨的定价是3.8元,那么你建议如何合理搭配
这三个品种的馄饨?
随堂练习
课本P136
3
(4)如果混合馄饨的定价是3.8元,那么你建议如何合理搭配
这三个品种的馄饨?
设3种馄饨的个数分别为x,y,z,
则x
+
y
+
z=10,
∴
0.3x+0.4y+0.5z=3.8.
∵
z=10-x-y,
∴只需满足2x+y=12即可.
∵
x,
y为正整数,且x+y<10,
∴方程2x+y=12的正整数解有:
∴
有三种搭配方案:
(1)菜馅馄饨3个,鸡蛋馅馄饨6个,肉馅馄饨1个;
(2)菜馅馄饨4个,鸡蛋馅馄饨4个,肉馅馄饨2个;
(3)菜馅馄饨5个,鸡蛋馅馄饨2个,肉馅馄饨3个.
2.某校九年级在一次广播操比赛中,三个班的各项得分
如下表:
(1)填空:根据表中提供的信息,在服装统一方面,三个班得分的平均数是
;在动作准确方面最有优势的是
班;
服装统一
动作整齐
动作准确
九(1)班
80
84
87
九(2)班
97
78
80
九(3)班
90
78
85
(2)如果服装统一,动作整齐,动作准确三个方面按20%,30%,
50%的比例计算各班的得分,请通过计算说明哪个班的得分最高?
89
九(1)
九(1)班的平均得分为:80×20%
+
84×30%
+
87×50%
=
84.7
(分),
九(2)班的平均得分为:97×20%
+
78×30%
+
80×50%
=
82.8
(分),
九(3)班的平均得分为:90×20%
+
78×30%
+
85×50%
=
83.9
(分),
∴得分最高的是九(1)班.
各个指标在总结果中所占的百分比称为每个指标的权重.
定义:一般地,如果n个数据中,
x1出现了f1次,
x2出现了f2次,
……,xk出现了fk次(f1+f2+…+fk=n),那么我们把
叫做这n个数的加权平均数.
权重
课堂小结
各个指标乘以相应的权重后的和叫做加权平均数.
(1)当一组数据中某些数据重复出现时,则选用加权平均数
公式求平均数;
(2)在加权平均数公式中,分子是各数据与其权乘积的和;
分母是权的和,不能简单地看成数据个数之和;
(3)常见的权的形式:分数;出现的次数(个数);权的比例关系.
作业与课外学习任务
1.练习:学习检测P78-79
第1至10题
作业:课本P138
习题20.1
5,6,7
2.课外学习任务:
预习课本:P140-143
20.2.1
中位数和众数
教学反馈:
作业存在的主要问题:
20.1.3
加权平均数
第20章
数据的整理与初步处理
教学目标
教学重点与难点
重点:加权平均数的概念及其求法.
难点:用加权平均数解决实际问题.
1.理解和掌握加权平均数的概念.
2.会用加权平均数解决实际生活中的问题.
平均数的概念:
一组数据的总和与这组数据的个数之比叫做这组数据的平均数.
(或算术平均数)
公式表示:
设有一组数据x1,x2,
x3,···
,
xn,
则该组数据的平均数为:
说明:
(1)平均数是体现这组数据的平均水平;
(2)一组数据的平均数有且只有一个.
温故夯基
巩固练习
1.如果一组数据85,80,x,90的平均数是85,则x=____.
2.某学生在一次考试中,语文、数学、英语三门学科的平均分为80分,物理、政治两科的平均分为85,则该生这5门学科的平均分为____.
3.某班共有50名学生,平均身高为168cm,其中30名男生的平均身高为170cm,则20名女生的平均身高为________.
85
82
165
cm
4.在某捐款活动中,九年级某班的同学捐出了自己的零花钱
.现将同学们的捐款数整理成统计表,则该班同学平均每人捐款
元.
捐款数(元)
5
10
20
50
人数
4
17
6
13
24
在日常生活中,我们经常会与平均数打交道,但有时发现以前计算平均数的方法并不适用.
学习新知
(1)商店里有两种苹果,一种单价为
3.50
元/千克,另一种单价为
6
元/千克.小明妈妈买了单价为
3.50
元/千克的苹果
1
千克,单价为
6
元/千克的苹果
3
千克,那么小明妈妈所买苹果的平均价格是两个单价相加除以
2
吗?为什么?
不是
既然不是,你会怎么计算
所买苹果的平均价格呢?
(2)老师在计算学生每学期的总评成绩时,并不是简单地将一个学生的平时成绩与考试成绩相加除以2,而是按照“平时成绩占
40%,考试成绩占
60%”的比例计算(如图),其中考试成绩更为重要.
如果一个学生的平时成绩为
70
分,考试成绩为
90
分,那么他的学期总评成绩是多少?
70
×
40%
+
90
×
60%
=
82(分)
权重
考试60%
平时40%
解:该学生的学期总评成绩是:
加权平均数
考试60%
平时40%
一般来说,由于各个指标在总结果中占有不同的重要性,因而会被赋予不同的权重.
各个指标在总结果中所占的
百分比称为每个指标的权重.
各个指标乘以相应的权重后的和叫做加权平均数.
定义:一般地,如果n个数据中,
x1出现了f1次,
x2出现了f2次,
……,xk出现了fk次(f1+f2+…+fk=n),那么我们把
叫做这n个数的加权平均数.
权重
加权平均数
权重
说明:
(1)当一组数据中某些数据重复出现时,则选用加权平均数
公式求平均数;
(2)在加权平均数公式中,分子是各数据与其权乘积的和;
分母是权的和,不能简单地看成数据个数之和;
(3)常见的权的形式:分数;出现的次数(个数);权的比例关系;
(4)算术平均数是加权平均数的特殊形式,特殊在各项的权
相等.
小青七年级第二学期的数学成绩分别为:测验一得
89分,测验二得
78分,测验三得
85分,期中考试得
90分,期末考试得
87分.如果按照图中所显示的平时、期中、期末成绩的权重,那么小青该学期的总评成绩是多少?
期末60%
平时10%
期中30%
试一试
解:小青的平时平均成绩为
89
+
78
+
85
3
=
84,
∴
小青该学期的总评成绩为
84
×
10%
+
90×30%
+
87
×
60%
=
87.6
.
=
8.4+27+52.2
1.某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是(
).
A.
80分
B.
82分
C.
84分
D.
86分
D
随堂练习
3.某学习小组共有学生5人,在一次数学测验中,有2人得85分,2人得90分,1人得70分,该学习小组的平均分是
分.
84
2.某次军训打靶,有a次每次中靶x环,有b次每次中靶y环,
则这个人平均每次中靶的环数是(
).
B
4.在实施清洁工作的过程中,某校对各个班级教室卫生
情况的考评包括以下几项:黑板、门窗、桌椅、地面。
一天,两个班级的各项卫生成绩(单位:分)分别如下表:
黑板
门窗
桌椅
地面
一班
95
85
89
91
二班
90
95
85
90
班级
成绩
项目
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这四项得分依次按15%,10%,35%,40%
的比例计算各班的卫生成绩,那么哪个班的卫生成绩高?请说明理由.
(1)两个班的平均得分分别是多少?
解:(1)一班的平均得分是(95+85+89+91)÷4
=90,
二班的平均得分是(90+95+85+90)÷4
=90.
黑板
门窗
桌椅
地面
一班
95
85
89
91
二班
90
95
85
90
班级
成绩
项目
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这四项得分依次按15%,10%,35%,40%
的比例计算各班的卫生成绩,那么哪个班的卫生成绩高?请说明理由.
(2)一班的加权平均成绩是
95×15%+85×10%+89×35%+91×40%
=14.25+8.5+31.15+36.4
=90,
二班的加权平均成绩是
90×15%+95×10%+85×35%+90×40%
=13.5+9.5+29.75+36
=88.75,
∴一班的卫生成绩高.
某公司对应聘者
A、B、C、D
进行面试,并按三个方面给应聘者打分,每个方面满分20
分,最后打分结果如表所示.如果你是人事主管,会录用哪一位应聘者?
A
B
C
D
专业知识
14
18
17
16
工作经验
18
16
14
16
仪表形象
12
11
14
14
问题探索
总分得分
44
45
45
46
对上述问题,甲同学说:看谁的总分高就录用谁.
通过计算可以发现
D
的总分最高,应该被录用.
这时乙同学说:我有不同意见.三个方面满分都是
20
分,但按理这三个方面的重要性应该有所不同,比如专业知识就应该比仪表形象更重要.
你认为谁的说法比较合理?
乙更合理
假设上述三个方面的重要性之比为
6:3:1,如图所示,那么应该录用谁呢?
专业知识
工作经验
仪表形象
因为
6:3:1
=
60%:30%:10%,
问题探索
所以专业知识、工作经验与仪表形象这三个方面的权重分别是
60%、30%
与
10%.
∵A最后得分为14×60%
+
18×30%
+
12×10%
=
15,
B最后得分为18×60%
+
16×30%
+
11×10%
=
16.7,
C最后得分为17×60%
+
14×30%
+
14×10%
=
15.8,
D最后得分为16×60%
+
16×30%
+
14×10%
=
15.8,
∴
应该录用B.
如果这三个方面的重要性之比为
10:7:3,此时三个方面的权重各是多少?哪一位应该被录用?
A
B
C
D
专业知识
14
18
17
16
工作经验
18
16
14
16
仪表形象
12
11
14
14
10:7:
3
=
50%:35%:15%
问题探索
∵A最后得分为14×50%
+
18×35%
+
12×15%
=
15.1,
B最后得分为18×50%
+
16×35%
+
11×15%
=
16.25,
C最后得分为17×50%
+
14×35%
+
14×15%
=
15.5,
D最后得分为16×50%
+
16×35%
+
14×15%
=
15.7,
∴
应该录用B.
随堂练习
1.
一家小吃店原有三个品种的馄饨,其中菜馅馄饨的售价
为3元/碗,鸡蛋馅馄饨的售价为4元/碗,肉馅馄饨的售价
为5元/碗.每碗均有10个馄饨.该店老板准备推出混合馄饨,
请帮她解决以下问题:
课本P136
3
(1)如果每碗有3个菜馅的、3个鸡蛋馅的、4个肉馅的馄饨,
那么混合馄饨每碗的定价应是多少?
∵菜馅,鸡蛋馅,肉馅单个馄饨价分别为0.3元,0.4元,0.5元,
∴
混合馄饨每碗的定价为:0.3×3+0.4×3+0.5×4=4.1(元).
(2)如果菜馅、鸡蛋馅、肉馅馄饨的个数之比为3∶2∶5,
那么混合馄饨的每碗定价应是多少?
∵菜馅,鸡蛋馅,肉馅单个馄饨价分别为0.3元,0.4元,0.5元,
∴
混合馄饨每碗的定价为:0.3×3+0.4×2+0.5×5=4.2(元).
随堂练习
1.
一家小吃店原有三个品种的馄饨,其中菜馅馄饨的售价
为3元/碗,鸡蛋馅馄饨的售价为4元/碗,肉馅馄饨的售价
为5元/碗.每碗均有10个馄饨.该店老板准备推出混合馄饨,
请帮她解决以下问题:
课本P136
3
∵菜馅,鸡蛋馅,肉馅单个馄饨价分别为0.3元,0.4元,0.5元,
∴
混合馄饨每碗的定价为:0.3×2+0.4×2+0.5×6=4.4(元).
(3)如果菜馅、鸡蛋馅、肉馅馄饨的个数之比为1∶1∶3,
那么混合馄饨的每碗定价应是多少?
(4)如果混合馄饨的定价是3.8元,那么你建议如何合理搭配
这三个品种的馄饨?
随堂练习
课本P136
3
(4)如果混合馄饨的定价是3.8元,那么你建议如何合理搭配
这三个品种的馄饨?
设3种馄饨的个数分别为x,y,z,
则x
+
y
+
z=10,
∴
0.3x+0.4y+0.5z=3.8.
∵
z=10-x-y,
∴只需满足2x+y=12即可.
∵
x,
y为正整数,且x+y<10,
∴方程2x+y=12的正整数解有:
∴
有三种搭配方案:
(1)菜馅馄饨3个,鸡蛋馅馄饨6个,肉馅馄饨1个;
(2)菜馅馄饨4个,鸡蛋馅馄饨4个,肉馅馄饨2个;
(3)菜馅馄饨5个,鸡蛋馅馄饨2个,肉馅馄饨3个.
2.某校九年级在一次广播操比赛中,三个班的各项得分
如下表:
(1)填空:根据表中提供的信息,在服装统一方面,三个班得分的平均数是
;在动作准确方面最有优势的是
班;
服装统一
动作整齐
动作准确
九(1)班
80
84
87
九(2)班
97
78
80
九(3)班
90
78
85
(2)如果服装统一,动作整齐,动作准确三个方面按20%,30%,
50%的比例计算各班的得分,请通过计算说明哪个班的得分最高?
89
九(1)
九(1)班的平均得分为:80×20%
+
84×30%
+
87×50%
=
84.7
(分),
九(2)班的平均得分为:97×20%
+
78×30%
+
80×50%
=
82.8
(分),
九(3)班的平均得分为:90×20%
+
78×30%
+
85×50%
=
83.9
(分),
∴得分最高的是九(1)班.
各个指标在总结果中所占的百分比称为每个指标的权重.
定义:一般地,如果n个数据中,
x1出现了f1次,
x2出现了f2次,
……,xk出现了fk次(f1+f2+…+fk=n),那么我们把
叫做这n个数的加权平均数.
权重
课堂小结
各个指标乘以相应的权重后的和叫做加权平均数.
(1)当一组数据中某些数据重复出现时,则选用加权平均数
公式求平均数;
(2)在加权平均数公式中,分子是各数据与其权乘积的和;
分母是权的和,不能简单地看成数据个数之和;
(3)常见的权的形式:分数;出现的次数(个数);权的比例关系.
作业与课外学习任务
1.练习:学习检测P78-79
第1至10题
作业:课本P138
习题20.1
5,6,7
2.课外学习任务:
预习课本:P140-143
20.2.1
中位数和众数
教学反馈:
作业存在的主要问题:
