20.3数据的离散程度(方差)-2020-2021学年华东师大版八年级数学下册课件(27张)
文档属性
| 名称 | 20.3数据的离散程度(方差)-2020-2021学年华东师大版八年级数学下册课件(27张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 15:56:20 | ||
图片预览







文档简介
(共27张PPT)
20.3
数据的离散程度
第20章
数据的整理与初步处理
1.方
差
教学目标
教学重点与难点
重点:对一组数据的方差的理解,会求一组数据的方差.
难点:对方差的理解及应用.
1.通过对实际问题的分析,让学生体会引入方差刻画数据离散程度的必要性及意义.
2.理解和掌握方差公式,并会应用.
一.平均数的概念:
一组数据的总和与这组数据的个数之比叫做这组数据的平均数.
(或算术平均数)
温故夯基
二.加权平均数的概念:
各个指标乘以相应的权重后的和叫做加权平均数.
三.中位数的概念:
将一组数据按照由小到大(或由大到小)的顺序排列.
如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;
如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
四.众数的概念:
一组数据中出现次数最多的那个数据就是这组数据的众数.
巩固练习
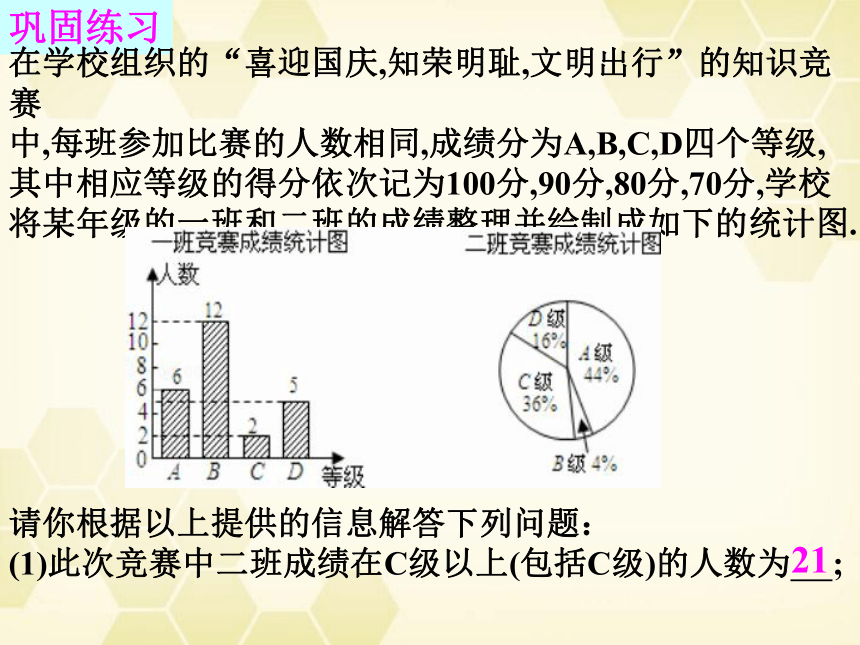
在学校组织的“喜迎国庆,知荣明耻,文明出行”的知识竞赛
中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,
其中相应等级的得分依次记为100分,90分,80分,70分,学校
将某年级的一班和二班的成绩整理并绘制成如下的统计图.
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为 ?;
21
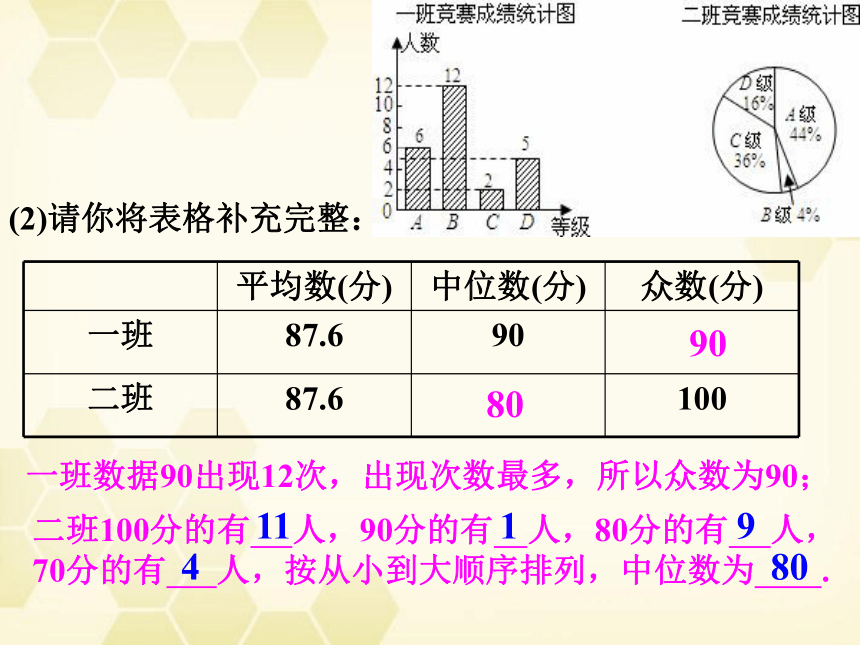
(2)请你将表格补充完整:
平均数(分)
中位数(分)
众数(分)
一班
87.6
90
二班
87.6
100
一班数据90出现12次,出现次数最多,所以众数为90;
90
二班100分的有
人,90分的有
人,80分的有
人,
70分的有
人,按从小到大顺序排列,中位数为
.
11
1
9
4
80
80
(3)请从下列不同角度对这次竞赛成绩的结果进行分析:
①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从B级以上(包括B级)的人数的角度来比较一班和二班的
成绩.
平均数(分)
中位数(分)
众数(分)
一班
87.6
90
90
二班
87.6
80
100
从平均数的角度看两班成绩一样,从中位数的角度看一班
比二班的成绩好,所以一班成绩好
.
从平均数的角度看两班成绩一样,从众数的角度看二班
比一班的成绩好,所以二班成绩好.
从B级以上(包括B级)的人数的角度看,一班人数是
18人,二班人数是12人,所以一班成绩好.
我们常用平均数、中位数来刻画数据的“平均水平”,但在有些情况下“平均水平”是不够的,如评价选手的射击水平、机器加工零件的精度、手表的日走时误差时,还需要用一个新的数来刻画一组数据的波动情况.
新课导入
它就是—方差.
问题探索
问题1:下表显示的是上海2001年2月下旬和2002年同期
的每日最高气温:
上海市每日最高气温统计表(单位:℃)
2月21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
12
10
从表中可以看出,2002年2月下旬和2001年同期的
气温相比,有4天的气温相对高些,有3天的气温
相对低些,还有1天的气温相同.我们可以由此认为
2002年2月下旬的气温比2001年同期高吗?
不可以
问题探索
问题1:下表显示的是上海2001年2月下旬和2002年同期
的每日最高气温:
上海市每日最高气温统计表(单位:℃)
2月21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
12
10
从表中可以看出,2002年2月下旬和2001年同期的
气温相比,有4天的气温相对高些,有3天的气温
相对低些,还有1天的气温相同.我们可以由此认为
2002年2月下旬的气温比2001年同期高吗?
不可以
比较两段时间气温的高低,求平均气温是一种常用的方法.
上海市每日最高气温统计表(单位:℃)
问题探索
2月21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
12
10
经计算可以看出,对于2月下旬的这段时间而言,
2001年和2002年上海市平均气温相等,都是12℃.这是不是说,两个时段的气温情况总体上没有什么差异呢?
不是
右图是根据两段时间的
气温情况绘成的折线图.
问题探索
观察一下,它们有差异吗?
通过观察,我们可以发现:
图(1)中的折线高低起伏
比较大—从6
℃到22℃
,
图(2)中的折线高低起伏
比较小—从9
℃到16
℃.
图(1)中气温的最大值与最小值之间差距很大,相差16
℃;
图(2)中气温的最大值与最小值相差7
℃,总体上气温变化的范围不太大.
学习新知
一.极差
我们可以用一组数据中的最大值减去最小值所得
的差来反映这组数据的变化范围,
用这种方法得到
的差称为极差.
极差公式:
极差=最大值-最小值
思考:
为什么说本章导图中的两个城市,一个“四季温差
不大”,一个“四季分明”?
用数学术语应该怎样表示呢?
测试次数
1
2
3
4
5
小明
10
14
13
12
13
小兵
11
11
15
14
11
问题探索
问题2:小明和小兵两人参加体育项目训练,近期的
5次测试成绩如下表所示.请问谁的成绩较为稳定?
为什么?
(1)小明的平均成绩是
,极差是
;
小兵的平均成绩是
,极差是
.
12.4
4
12.4
4
(2)谁的成绩比较为稳定呢?
平均数,极差都一样,该怎么办呢?
问题探索
把他们的成绩画图如下:
画出它们的折线图形
平均成绩
小明的成绩大部分
集中在平均数附近。
小兵的成绩与其平均数的离散程度略大!
通常,如果一组数据与其平均数的离散程度较小,
我们就说它比较稳定.
思考:怎样的指标能反映一组数据与其平均数的离散程度呢?
1
2
3
4
5
求和
小明
每次测试成绩
10
14
13
12
13
每次成绩-
平均成绩
小兵
每次测试成绩
11
11
15
14
11
每次成绩-
平均成绩
-2.4
1.6
0.6
-0.4
0.6
-1.4
-1.4
2.6
1.6
-1.4
0
0
思考:依据最后求和结果可以比较两组数据围绕平均数的波动情况吗?
问题探索
我们已经看出,小兵的测试成绩与平均数的偏差与小明
相比略大.那么如何加以说明呢?可以直接将各数据与平均数的差进行累加吗?在表中写出你的计算结果.
如果不行,请你提出一个可行的方案.
1
2
3
4
5
求平
方和
小明
每次测试成绩
10
14
13
12
13
每次成绩-
平均成绩
-2.4
1.6
0.6
-0.4
0.6
小兵
每次测试成绩
11
11
15
14
11
每次成绩-
平均成绩
-1.4
-1.4
2.6
1.6
-1.4
在上表的基础上求每次成绩与平均成绩差的平方和:
9.2
15.2
思考:依据最后求平方和的结果可以比较两组数据围绕
平均数的波动情况吗?
问题探索
5.76
2.56
0.36
0.16
0.36
1.96
1.96
6.76
2.56
1.96
可以
1
2
3
4
5
6
7
求平
方和
小
明
每次测试
成绩
10
14
13
缺席
12
缺席
13
每次成绩-
平均成绩
-2.4
1.6
0.6
-0.4
0.6
小
兵
每次测试
成绩
11
11
15
11
14
14
11
每次成绩-
平均成绩
-1.4
-1.4
2.6
-1.4
1.6
1.6
-1.4
思考:如果一共进行了7次测试,小明因故缺席了2次,怎样比较谁的成绩更稳定?请将你的方法与数据填入下表:
9.2
19.72
思考:依据求平方和的结果可以准确比较两组数据的波动情况吗?
再求
平均
1.84
2.81
不能,因为次数不一样.
那怎样才合适呢?
思考:依据最后再求平均的结果可以比较两组数据围绕
平均数的波动情况吗?
可以
学习新知
数据的离散程度—方差
我们可以用“先平均,再求差,然后平方,最后再平均”
得到的结果表示一组数据偏离平均值的情况.这个
结果通常称为方差.
通常用x1,x2,…,xn表示各个原始数据,
用
表示一组数据的平均数,
用s?表示一组数据的方差,
方差的计算公式就是:
要点说明
1.方差的计算可以概括为:
先平均,再求差,然后平方,最后再平均.
2.方差是反映一组数据波动大小的指标:
方差越小,离散程度越小,波动越小;
方差越大,离散程度越大,波动越大.
3.平均数、极差与方差的区别:
平均数—反映一组数据的总体趋势;
极
差—反映一组数据变化范围的大小;
方
差—描述一组数据的波动大小或者与平均值的
离散程度的大小.
则数字5,10分别表示这个样本的(
).
A.容量,平均数
B.平均数,中位数
C.众数,中位数
D.中位数,容量
例1
某个样本的方差为:
A
例题精析
例2
一组数据6,
4,
a,
3,
2的平均数是5,求这组数据的方差.
解:∵数据6,
4,
a,
3,
2的平均数是5,
∴6+4+a+3+2=5×5,
∴a=10.
∴这组数据的方差
=8
.
C
随堂练习
2.
某样本数据(单位:℃):12,
16,-6,
11,……,在计算它的
方差时,小明按以下算式进行计算:
则算式中的数15,20分别表示这个样本的(
).
A.众数,中位数
B.方差,众数
C.数据的个数,平均数
D.数据的个数,中位数
1.下列说法正确的是(
).
A.两组数据,平均数越大,波动越大
B.两组数据,中位数越大,波动越大
C.两组数据,方差越大,波动越大
D.两组数据的波动大小由平均数、方差共同说明
C
3.甲、乙、丙、丁四人参加体育训练,近期的10次百米测试平均成绩都是13.2秒,方差如下表:
B
选手
甲
乙
丙
丁
方差
0.020
0.019
0.021
0.022
则这四人中发挥最稳定的是(
).
A.
甲
B.
乙
C.
丙
D.
丁
4.在某中学矩形的演讲比赛中,七年级5名参赛选手的成绩
如下表所示.请你根据表中提供的数据,计算出这5名选手
成绩的方差是(
).
选手
1号
2号
3号
4号
5号
平均成绩
得分
90
95
93
89
88
91
A.
2
B.
93
C.
34
D.
6.8
D
5.为了响应学校“书香校园”建设,阳光班的同学们积极
捐书,某学习小组的同学捐书册数分别为:5,7,x,4,6.已知他们平均每人捐书5本,求这组数据的中位数和方差.
解:∵数据5,
7,
x,
4,
6的平均数是5,
∴
x=
3.
∴这组数据为:3,4,5,6,7,
∴这组数据的中位数是5.
这组数据的方差
=2
.
(1)甲队成绩的中位数是
分,乙队成绩的众数是
分;
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(2)计算乙队的平均成绩和方差;
解:乙队的平均成绩为:
则方差是:
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是
队.
6.某班组织了一次经典朗读比赛,甲、乙两队各10人的
比赛成绩如下表(10分制):
9.5
10
=1
.
乙
数据的离散程度—方差
通常用x1,x2,…,xn表示各个原始数据,
用
表示一组数据的平均数,
用s?表示一组数据的方差,
则方差的计算公式就是:
课堂小结
先平均,再求差,然后平方,最后再平均.
方差越小,离散程度越小,波动越小;
方差越大,离散程度越大,波动越大.
方差是反映一组数据波动大小的指标:
作业与课外学习任务
1.练习:学习检测P84-85
第1至12题
作业:课本P155
习题20.3
1,2,3
2.课外学习任务:
复习本章内容,准备单元检测.
教学反馈:
作业存在的主要问题:
20.3
数据的离散程度
第20章
数据的整理与初步处理
1.方
差
教学目标
教学重点与难点
重点:对一组数据的方差的理解,会求一组数据的方差.
难点:对方差的理解及应用.
1.通过对实际问题的分析,让学生体会引入方差刻画数据离散程度的必要性及意义.
2.理解和掌握方差公式,并会应用.
一.平均数的概念:
一组数据的总和与这组数据的个数之比叫做这组数据的平均数.
(或算术平均数)
温故夯基
二.加权平均数的概念:
各个指标乘以相应的权重后的和叫做加权平均数.
三.中位数的概念:
将一组数据按照由小到大(或由大到小)的顺序排列.
如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;
如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
四.众数的概念:
一组数据中出现次数最多的那个数据就是这组数据的众数.
巩固练习
在学校组织的“喜迎国庆,知荣明耻,文明出行”的知识竞赛
中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,
其中相应等级的得分依次记为100分,90分,80分,70分,学校
将某年级的一班和二班的成绩整理并绘制成如下的统计图.
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为 ?;
21
(2)请你将表格补充完整:
平均数(分)
中位数(分)
众数(分)
一班
87.6
90
二班
87.6
100
一班数据90出现12次,出现次数最多,所以众数为90;
90
二班100分的有
人,90分的有
人,80分的有
人,
70分的有
人,按从小到大顺序排列,中位数为
.
11
1
9
4
80
80
(3)请从下列不同角度对这次竞赛成绩的结果进行分析:
①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从B级以上(包括B级)的人数的角度来比较一班和二班的
成绩.
平均数(分)
中位数(分)
众数(分)
一班
87.6
90
90
二班
87.6
80
100
从平均数的角度看两班成绩一样,从中位数的角度看一班
比二班的成绩好,所以一班成绩好
.
从平均数的角度看两班成绩一样,从众数的角度看二班
比一班的成绩好,所以二班成绩好.
从B级以上(包括B级)的人数的角度看,一班人数是
18人,二班人数是12人,所以一班成绩好.
我们常用平均数、中位数来刻画数据的“平均水平”,但在有些情况下“平均水平”是不够的,如评价选手的射击水平、机器加工零件的精度、手表的日走时误差时,还需要用一个新的数来刻画一组数据的波动情况.
新课导入
它就是—方差.
问题探索
问题1:下表显示的是上海2001年2月下旬和2002年同期
的每日最高气温:
上海市每日最高气温统计表(单位:℃)
2月21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
12
10
从表中可以看出,2002年2月下旬和2001年同期的
气温相比,有4天的气温相对高些,有3天的气温
相对低些,还有1天的气温相同.我们可以由此认为
2002年2月下旬的气温比2001年同期高吗?
不可以
问题探索
问题1:下表显示的是上海2001年2月下旬和2002年同期
的每日最高气温:
上海市每日最高气温统计表(单位:℃)
2月21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
12
10
从表中可以看出,2002年2月下旬和2001年同期的
气温相比,有4天的气温相对高些,有3天的气温
相对低些,还有1天的气温相同.我们可以由此认为
2002年2月下旬的气温比2001年同期高吗?
不可以
比较两段时间气温的高低,求平均气温是一种常用的方法.
上海市每日最高气温统计表(单位:℃)
问题探索
2月21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
12
10
经计算可以看出,对于2月下旬的这段时间而言,
2001年和2002年上海市平均气温相等,都是12℃.这是不是说,两个时段的气温情况总体上没有什么差异呢?
不是
右图是根据两段时间的
气温情况绘成的折线图.
问题探索
观察一下,它们有差异吗?
通过观察,我们可以发现:
图(1)中的折线高低起伏
比较大—从6
℃到22℃
,
图(2)中的折线高低起伏
比较小—从9
℃到16
℃.
图(1)中气温的最大值与最小值之间差距很大,相差16
℃;
图(2)中气温的最大值与最小值相差7
℃,总体上气温变化的范围不太大.
学习新知
一.极差
我们可以用一组数据中的最大值减去最小值所得
的差来反映这组数据的变化范围,
用这种方法得到
的差称为极差.
极差公式:
极差=最大值-最小值
思考:
为什么说本章导图中的两个城市,一个“四季温差
不大”,一个“四季分明”?
用数学术语应该怎样表示呢?
测试次数
1
2
3
4
5
小明
10
14
13
12
13
小兵
11
11
15
14
11
问题探索
问题2:小明和小兵两人参加体育项目训练,近期的
5次测试成绩如下表所示.请问谁的成绩较为稳定?
为什么?
(1)小明的平均成绩是
,极差是
;
小兵的平均成绩是
,极差是
.
12.4
4
12.4
4
(2)谁的成绩比较为稳定呢?
平均数,极差都一样,该怎么办呢?
问题探索
把他们的成绩画图如下:
画出它们的折线图形
平均成绩
小明的成绩大部分
集中在平均数附近。
小兵的成绩与其平均数的离散程度略大!
通常,如果一组数据与其平均数的离散程度较小,
我们就说它比较稳定.
思考:怎样的指标能反映一组数据与其平均数的离散程度呢?
1
2
3
4
5
求和
小明
每次测试成绩
10
14
13
12
13
每次成绩-
平均成绩
小兵
每次测试成绩
11
11
15
14
11
每次成绩-
平均成绩
-2.4
1.6
0.6
-0.4
0.6
-1.4
-1.4
2.6
1.6
-1.4
0
0
思考:依据最后求和结果可以比较两组数据围绕平均数的波动情况吗?
问题探索
我们已经看出,小兵的测试成绩与平均数的偏差与小明
相比略大.那么如何加以说明呢?可以直接将各数据与平均数的差进行累加吗?在表中写出你的计算结果.
如果不行,请你提出一个可行的方案.
1
2
3
4
5
求平
方和
小明
每次测试成绩
10
14
13
12
13
每次成绩-
平均成绩
-2.4
1.6
0.6
-0.4
0.6
小兵
每次测试成绩
11
11
15
14
11
每次成绩-
平均成绩
-1.4
-1.4
2.6
1.6
-1.4
在上表的基础上求每次成绩与平均成绩差的平方和:
9.2
15.2
思考:依据最后求平方和的结果可以比较两组数据围绕
平均数的波动情况吗?
问题探索
5.76
2.56
0.36
0.16
0.36
1.96
1.96
6.76
2.56
1.96
可以
1
2
3
4
5
6
7
求平
方和
小
明
每次测试
成绩
10
14
13
缺席
12
缺席
13
每次成绩-
平均成绩
-2.4
1.6
0.6
-0.4
0.6
小
兵
每次测试
成绩
11
11
15
11
14
14
11
每次成绩-
平均成绩
-1.4
-1.4
2.6
-1.4
1.6
1.6
-1.4
思考:如果一共进行了7次测试,小明因故缺席了2次,怎样比较谁的成绩更稳定?请将你的方法与数据填入下表:
9.2
19.72
思考:依据求平方和的结果可以准确比较两组数据的波动情况吗?
再求
平均
1.84
2.81
不能,因为次数不一样.
那怎样才合适呢?
思考:依据最后再求平均的结果可以比较两组数据围绕
平均数的波动情况吗?
可以
学习新知
数据的离散程度—方差
我们可以用“先平均,再求差,然后平方,最后再平均”
得到的结果表示一组数据偏离平均值的情况.这个
结果通常称为方差.
通常用x1,x2,…,xn表示各个原始数据,
用
表示一组数据的平均数,
用s?表示一组数据的方差,
方差的计算公式就是:
要点说明
1.方差的计算可以概括为:
先平均,再求差,然后平方,最后再平均.
2.方差是反映一组数据波动大小的指标:
方差越小,离散程度越小,波动越小;
方差越大,离散程度越大,波动越大.
3.平均数、极差与方差的区别:
平均数—反映一组数据的总体趋势;
极
差—反映一组数据变化范围的大小;
方
差—描述一组数据的波动大小或者与平均值的
离散程度的大小.
则数字5,10分别表示这个样本的(
).
A.容量,平均数
B.平均数,中位数
C.众数,中位数
D.中位数,容量
例1
某个样本的方差为:
A
例题精析
例2
一组数据6,
4,
a,
3,
2的平均数是5,求这组数据的方差.
解:∵数据6,
4,
a,
3,
2的平均数是5,
∴6+4+a+3+2=5×5,
∴a=10.
∴这组数据的方差
=8
.
C
随堂练习
2.
某样本数据(单位:℃):12,
16,-6,
11,……,在计算它的
方差时,小明按以下算式进行计算:
则算式中的数15,20分别表示这个样本的(
).
A.众数,中位数
B.方差,众数
C.数据的个数,平均数
D.数据的个数,中位数
1.下列说法正确的是(
).
A.两组数据,平均数越大,波动越大
B.两组数据,中位数越大,波动越大
C.两组数据,方差越大,波动越大
D.两组数据的波动大小由平均数、方差共同说明
C
3.甲、乙、丙、丁四人参加体育训练,近期的10次百米测试平均成绩都是13.2秒,方差如下表:
B
选手
甲
乙
丙
丁
方差
0.020
0.019
0.021
0.022
则这四人中发挥最稳定的是(
).
A.
甲
B.
乙
C.
丙
D.
丁
4.在某中学矩形的演讲比赛中,七年级5名参赛选手的成绩
如下表所示.请你根据表中提供的数据,计算出这5名选手
成绩的方差是(
).
选手
1号
2号
3号
4号
5号
平均成绩
得分
90
95
93
89
88
91
A.
2
B.
93
C.
34
D.
6.8
D
5.为了响应学校“书香校园”建设,阳光班的同学们积极
捐书,某学习小组的同学捐书册数分别为:5,7,x,4,6.已知他们平均每人捐书5本,求这组数据的中位数和方差.
解:∵数据5,
7,
x,
4,
6的平均数是5,
∴
x=
3.
∴这组数据为:3,4,5,6,7,
∴这组数据的中位数是5.
这组数据的方差
=2
.
(1)甲队成绩的中位数是
分,乙队成绩的众数是
分;
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(2)计算乙队的平均成绩和方差;
解:乙队的平均成绩为:
则方差是:
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是
队.
6.某班组织了一次经典朗读比赛,甲、乙两队各10人的
比赛成绩如下表(10分制):
9.5
10
=1
.
乙
数据的离散程度—方差
通常用x1,x2,…,xn表示各个原始数据,
用
表示一组数据的平均数,
用s?表示一组数据的方差,
则方差的计算公式就是:
课堂小结
先平均,再求差,然后平方,最后再平均.
方差越小,离散程度越小,波动越小;
方差越大,离散程度越大,波动越大.
方差是反映一组数据波动大小的指标:
作业与课外学习任务
1.练习:学习检测P84-85
第1至12题
作业:课本P155
习题20.3
1,2,3
2.课外学习任务:
复习本章内容,准备单元检测.
教学反馈:
作业存在的主要问题:
