2020-2021学年华东师大版数学八年级下册19.2.1菱形的性质第1课时同步课件(共22张PPT)
文档属性
| 名称 | 2020-2021学年华东师大版数学八年级下册19.2.1菱形的性质第1课时同步课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 00:00:00 | ||
图片预览






文档简介
19.2.1 菱形的性质
情景导入
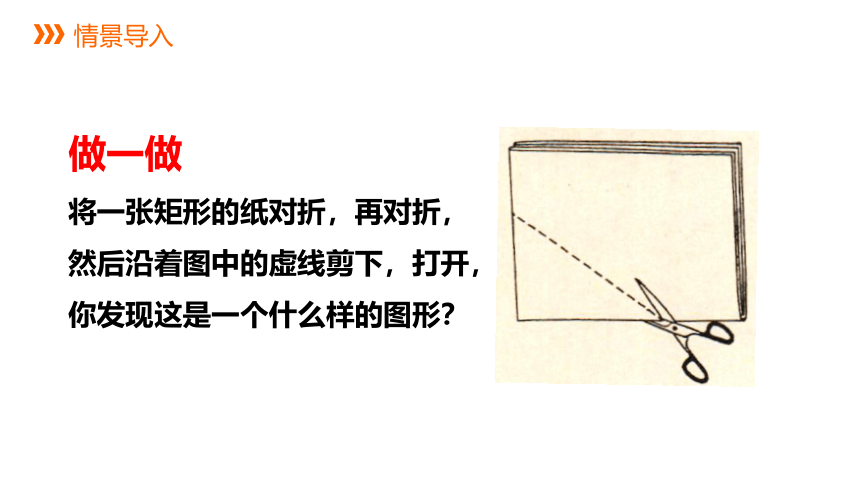
做一做
将一张矩形的纸对折,再对折,
然后沿着图中的虚线剪下,打开,
你发现这是一个什么样的图形?
情景导入
欣赏下面图片,图片中框出的图形是你熟悉的吗?
铁丝网
衣帽架
带图案的衣服
中国结
定义:有一组邻边相等的平行四边形叫做菱形.
(1)菱形必须满足两个条件:一是平行四边形; 二是一组邻边相等.二者必须同时具备,缺一不可;
(2)菱形的定义既是菱形的基本性质,也是菱形的基本判定方法.
获取新知
思考
菱形是一种特殊的平行四边形,它有什么性质?
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}
对称性
边
角
对角线
平行四边形的
一般性质
中心对称
菱形的特殊性质
如图,我们发现,菱形既是中
心对称图形,也是轴对称图形,
对称轴为它的对角线所在的直线.
菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
对称性:是轴对称图形.
边:四条边都相等.
对角线:互相垂直,且每
条对角线平分一组对角.
角:对角相等.
边:对边平行且相等.
对角线:相互平分.
菱形的特殊性质
平行四边形的性质
归纳总结
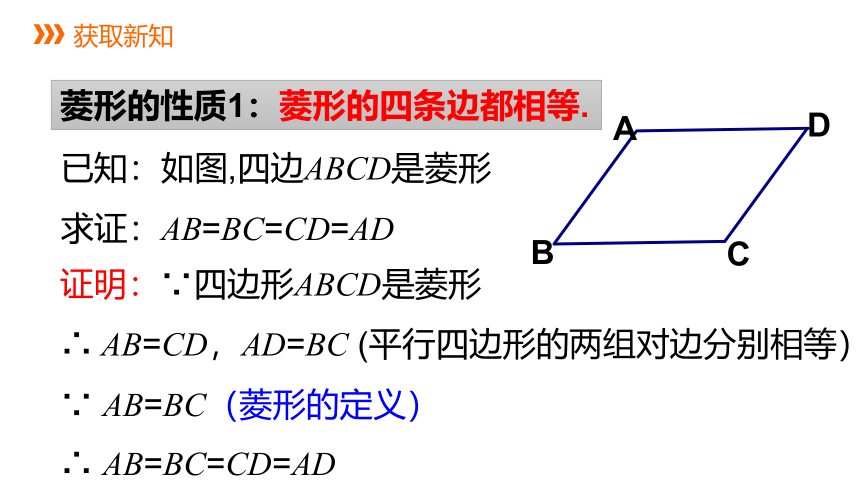
菱形的性质1:菱形的四条边都相等.
已知:如图,四边ABCD是菱形
求证:AB=BC=CD=AD
A
B
C
D
证明:∵四边形ABCD是菱形
∴ AB=CD,AD=BC (平行四边形的两组对边分别相等)
∵ AB=BC(菱形的定义)
∴ AB=BC=CD=AD
获取新知
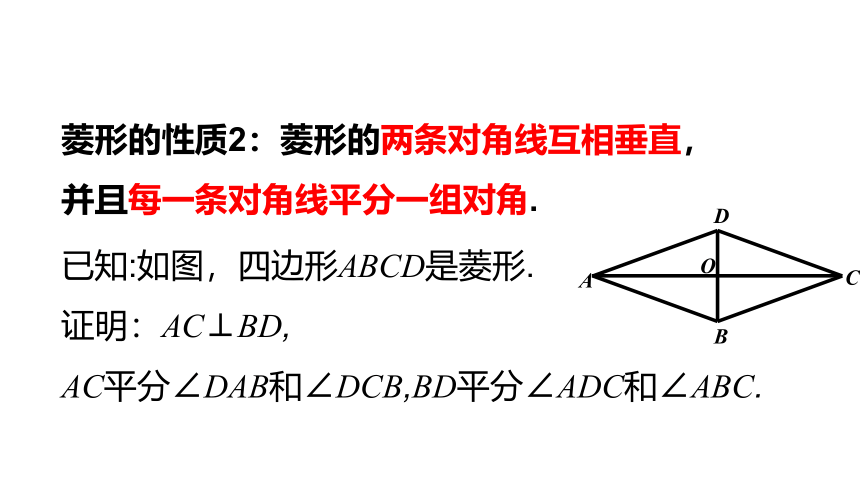
菱形的性质2:菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角.
已知:如图,四边形ABCD是菱形.
证明:AC⊥BD,
AC平分∠DAB和∠DCB,BD平分∠ADC和∠ABC.
A
B
C
D
O
证明:∵四边形ABCD是菱形,
∴AD=AB(菱形的定义),
OD=OB (平行四边形的对角线互相平分),
∴ AC ⊥ DB ,AC平分∠DAB(三线合一).
同理: AC平分∠DCB ;DB平分∠ADC和∠ABC.
A
B
C
D
O
例题讲解
例1 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的大小,并说明△ABC是等边三角形.
解:在菱形ABCD中,
AB=BC
∠B+∠BAD=180°
又已知∠BAD=2∠B
可得∠B=60°
所以△ABC是一个角为60°的等腰三角形,即为等边三角形.
A
B
C
D
归纳总结
一:菱形的四条边都相等
几何语言:
∵四边形ABCD是平行四边形
∴AB=BC=CD=AD
二:菱形的对角线互相垂直,且平分一组对角
几何语言:
∵四边形ABCD是平行四边形
∴AC⊥BD,∠DAC=∠BAC,∠DCA和∠BCA
∠ADB=∠CDB,∠ABD和∠CBD
A
B
C
D
O
┐
例2 如图,已知菱形ABCD的边长为 2 cm,∠BAD=120°,对角线AC、BD相交于点O. 试求这 个菱形的两条对角线AC与BD的长. (结果保留根号)
例题讲解
解:
∵四边形ABCD是菱形,
∴OB=OD,AB=AD(菱形的四条边都相等).
在△ABO和△ADO中,
∵AB=AD,AO=AO, OB=OD,
∴△ABO≌△ADO,
∴∠BAO=∠DAO = ∠BAD=60°.
在△ABC中,∵AB=BC,∠BAC=60°,
∴△ABC为等边三角形,∴AC=AB=2.
在菱形ABCD中,
∵AC⊥BD(菱形的对角线互相垂直),
∴△AOB为直角三角形,
∴
∴
例3 如图,菱形ABCD的对角线AC与BD 相交于点O,AE垂直且平分CD,垂足为点E. 求∠BCD的大小.
∵四边形ABCD是菱形,
∴AD=DC=CB=BA(菱形的
四条边都相等).
又∵AE垂直平分CD,
∴AC=AD,
∴AC=AD=DC=CB=BA,
即△ADC与△ABC都为等边三角形,
∴∠ACD=∠ACB=60°.
∴∠BCD=120°.
随堂演练
1.菱形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等
C.对角线互相垂直 D.对角线相等
C
2.如图,在菱形ABCD中,E,F分别是AB,AC的中点,如果EF=2,那么线段CD的长是( )
A.4 B.8 C.12 D.16
A
3.如图,在菱形ABCD中,AC=8,BD=6,则△ABD的周长等于( )
A.18 B.16 C.15 D.14
B
4. 如图,在△ABC中,AB=AC,四边形ADEF是菱形.
求证:BE=CE.
证明:∵四边形ADEF是菱形,
∴DE=FE,AB//FE,DE//AC,
∴∠B=∠CEF,∠C=∠BED.
∵AB=AC,
∴∠B=∠C,
∴∠BED=∠CEF.
在△DBE和△FCE中,
∵∠B=∠C,∠BED=∠CEF,DE=FE,
∴△DBE≌△FCE,
∴BE=CE.
课堂小结
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
情景导入
做一做
将一张矩形的纸对折,再对折,
然后沿着图中的虚线剪下,打开,
你发现这是一个什么样的图形?
情景导入
欣赏下面图片,图片中框出的图形是你熟悉的吗?
铁丝网
衣帽架
带图案的衣服
中国结
定义:有一组邻边相等的平行四边形叫做菱形.
(1)菱形必须满足两个条件:一是平行四边形; 二是一组邻边相等.二者必须同时具备,缺一不可;
(2)菱形的定义既是菱形的基本性质,也是菱形的基本判定方法.
获取新知
思考
菱形是一种特殊的平行四边形,它有什么性质?
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}
对称性
边
角
对角线
平行四边形的
一般性质
中心对称
菱形的特殊性质
如图,我们发现,菱形既是中
心对称图形,也是轴对称图形,
对称轴为它的对角线所在的直线.
菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
对称性:是轴对称图形.
边:四条边都相等.
对角线:互相垂直,且每
条对角线平分一组对角.
角:对角相等.
边:对边平行且相等.
对角线:相互平分.
菱形的特殊性质
平行四边形的性质
归纳总结
菱形的性质1:菱形的四条边都相等.
已知:如图,四边ABCD是菱形
求证:AB=BC=CD=AD
A
B
C
D
证明:∵四边形ABCD是菱形
∴ AB=CD,AD=BC (平行四边形的两组对边分别相等)
∵ AB=BC(菱形的定义)
∴ AB=BC=CD=AD
获取新知
菱形的性质2:菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角.
已知:如图,四边形ABCD是菱形.
证明:AC⊥BD,
AC平分∠DAB和∠DCB,BD平分∠ADC和∠ABC.
A
B
C
D
O
证明:∵四边形ABCD是菱形,
∴AD=AB(菱形的定义),
OD=OB (平行四边形的对角线互相平分),
∴ AC ⊥ DB ,AC平分∠DAB(三线合一).
同理: AC平分∠DCB ;DB平分∠ADC和∠ABC.
A
B
C
D
O
例题讲解
例1 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的大小,并说明△ABC是等边三角形.
解:在菱形ABCD中,
AB=BC
∠B+∠BAD=180°
又已知∠BAD=2∠B
可得∠B=60°
所以△ABC是一个角为60°的等腰三角形,即为等边三角形.
A
B
C
D
归纳总结
一:菱形的四条边都相等
几何语言:
∵四边形ABCD是平行四边形
∴AB=BC=CD=AD
二:菱形的对角线互相垂直,且平分一组对角
几何语言:
∵四边形ABCD是平行四边形
∴AC⊥BD,∠DAC=∠BAC,∠DCA和∠BCA
∠ADB=∠CDB,∠ABD和∠CBD
A
B
C
D
O
┐
例2 如图,已知菱形ABCD的边长为 2 cm,∠BAD=120°,对角线AC、BD相交于点O. 试求这 个菱形的两条对角线AC与BD的长. (结果保留根号)
例题讲解
解:
∵四边形ABCD是菱形,
∴OB=OD,AB=AD(菱形的四条边都相等).
在△ABO和△ADO中,
∵AB=AD,AO=AO, OB=OD,
∴△ABO≌△ADO,
∴∠BAO=∠DAO = ∠BAD=60°.
在△ABC中,∵AB=BC,∠BAC=60°,
∴△ABC为等边三角形,∴AC=AB=2.
在菱形ABCD中,
∵AC⊥BD(菱形的对角线互相垂直),
∴△AOB为直角三角形,
∴
∴
例3 如图,菱形ABCD的对角线AC与BD 相交于点O,AE垂直且平分CD,垂足为点E. 求∠BCD的大小.
∵四边形ABCD是菱形,
∴AD=DC=CB=BA(菱形的
四条边都相等).
又∵AE垂直平分CD,
∴AC=AD,
∴AC=AD=DC=CB=BA,
即△ADC与△ABC都为等边三角形,
∴∠ACD=∠ACB=60°.
∴∠BCD=120°.
随堂演练
1.菱形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等
C.对角线互相垂直 D.对角线相等
C
2.如图,在菱形ABCD中,E,F分别是AB,AC的中点,如果EF=2,那么线段CD的长是( )
A.4 B.8 C.12 D.16
A
3.如图,在菱形ABCD中,AC=8,BD=6,则△ABD的周长等于( )
A.18 B.16 C.15 D.14
B
4. 如图,在△ABC中,AB=AC,四边形ADEF是菱形.
求证:BE=CE.
证明:∵四边形ADEF是菱形,
∴DE=FE,AB//FE,DE//AC,
∴∠B=∠CEF,∠C=∠BED.
∵AB=AC,
∴∠B=∠C,
∴∠BED=∠CEF.
在△DBE和△FCE中,
∵∠B=∠C,∠BED=∠CEF,DE=FE,
∴△DBE≌△FCE,
∴BE=CE.
课堂小结
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
