2020-2021学年华东师大版八年级数学下册第18章平行四边形(小结与复习)课件(共13张PPT)
文档属性
| 名称 | 2020-2021学年华东师大版八年级数学下册第18章平行四边形(小结与复习)课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 521.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 15:08:15 | ||
图片预览

文档简介
(共13张PPT)
小
结
与
复
习
第18章
平行四边形
几
何
语
言
文字叙述
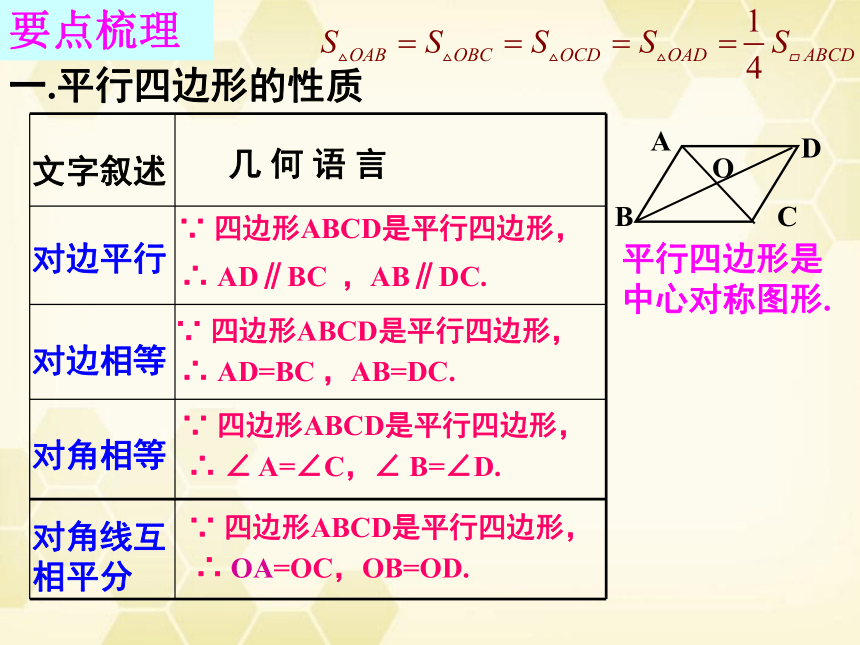
对边平行
对边相等
对角相等
∴
AD=BC
,AB=DC.
∵
四边形ABCD是平行四边形,
∴
∠
A=∠C,∠
B=∠D.
∵
四边形ABCD是平行四边形,
一.平行四边形的性质
对角线互
相平分
∵
四边形ABCD是平行四边形,
∴
OA=OC,OB=OD.
∵
四边形ABCD是平行四边形,
∴
AD∥BC
,AB∥DC.
平行四边形是
中心对称图形.
A
B
C
D
O
要点梳理
几
何
语
言
文字叙述
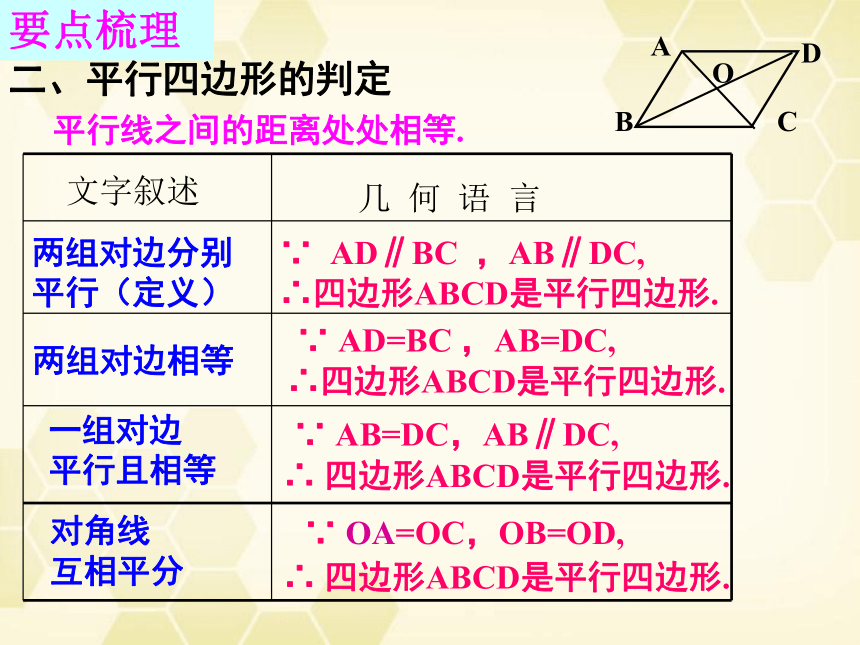
两组对边相等
一组对边
平行且相等
∴四边形ABCD是平行四边形.
∵
AD=BC
,AB=DC,
∴
四边形ABCD是平行四边形.
∵
AB=DC,AB∥DC,
二、平行四边形的判定
对角线
互相平分
∴
四边形ABCD是平行四边形.
∵
OA=OC,OB=OD,
两组对边分别平行(定义)
∴四边形ABCD是平行四边形.
∵
AD∥BC
,AB∥DC,
平行线之间的距离处处相等.
要点梳理
A
B
C
D
O
考点过关
考点一
平行四边形的性质与判定
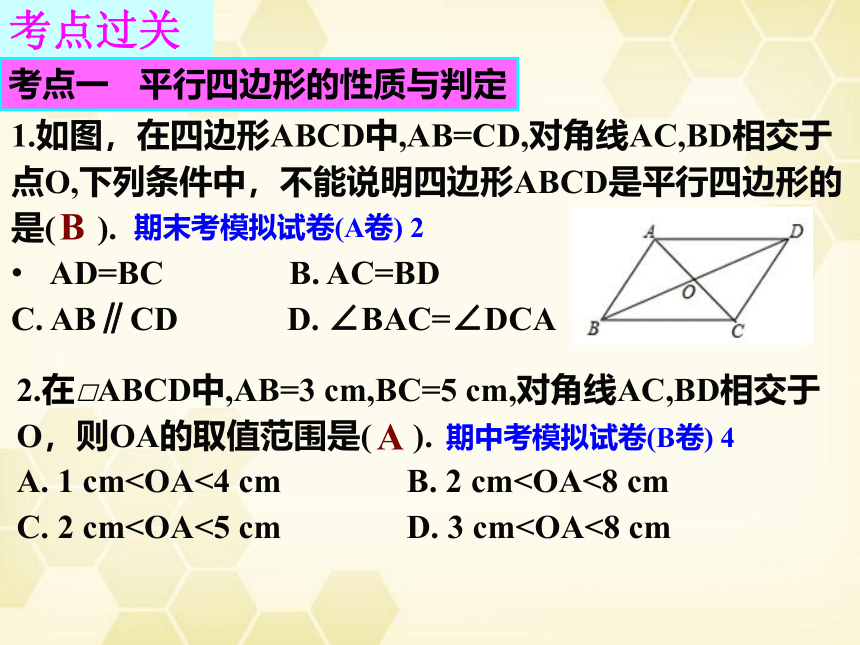
1.如图,在四边形ABCD中,AB=CD,对角线AC,BD相交于
点O,下列条件中,不能说明四边形ABCD是平行四边形的
是(
).
AD=BC
B.
AC=BD
C.
AB∥CD
D.
∠BAC=∠DCA
期末考模拟试卷(A卷)
2
B
2.在□ABCD中,AB=3
cm,BC=5
cm,对角线AC,BD相交于
O,则OA的取值范围是(
).
A.
1
cmcm
B.
2
cmcm
C.
2
cmcm
D.
3
cmcm
期中考模拟试卷(B卷)
4
A
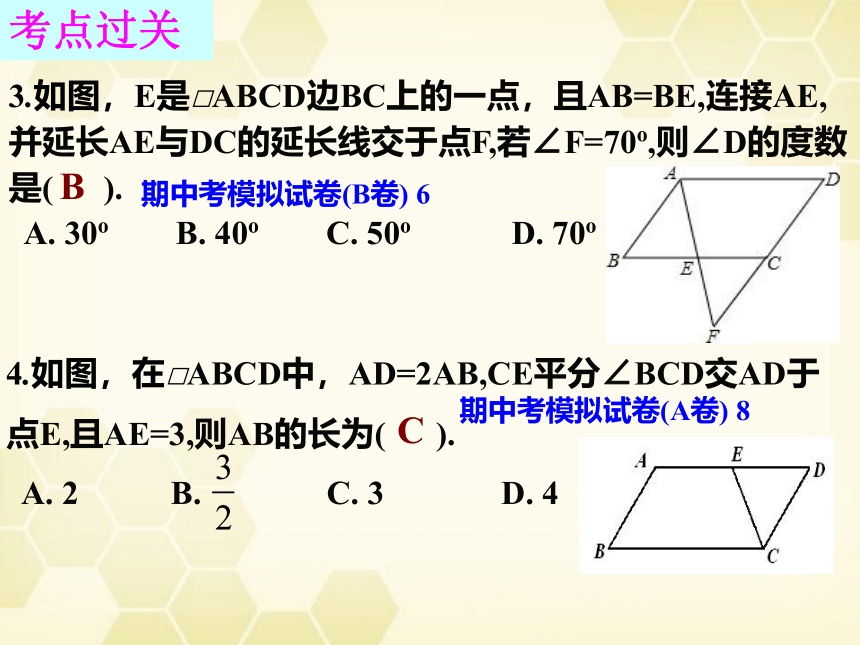
3.如图,E是□ABCD边BC上的一点,且AB=BE,连接AE,
并延长AE与DC的延长线交于点F,若∠F=70o,则∠D的度数
是(
).
A.
30o
B.
40o
C.
50o
D.
70o
考点过关
B
期中考模拟试卷(B卷)
6
4.如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD于
点E,且AE=3,则AB的长为(
).
A.
2
B.
C.
3
D.
4
期中考模拟试卷(A卷)
8
C
考点过关
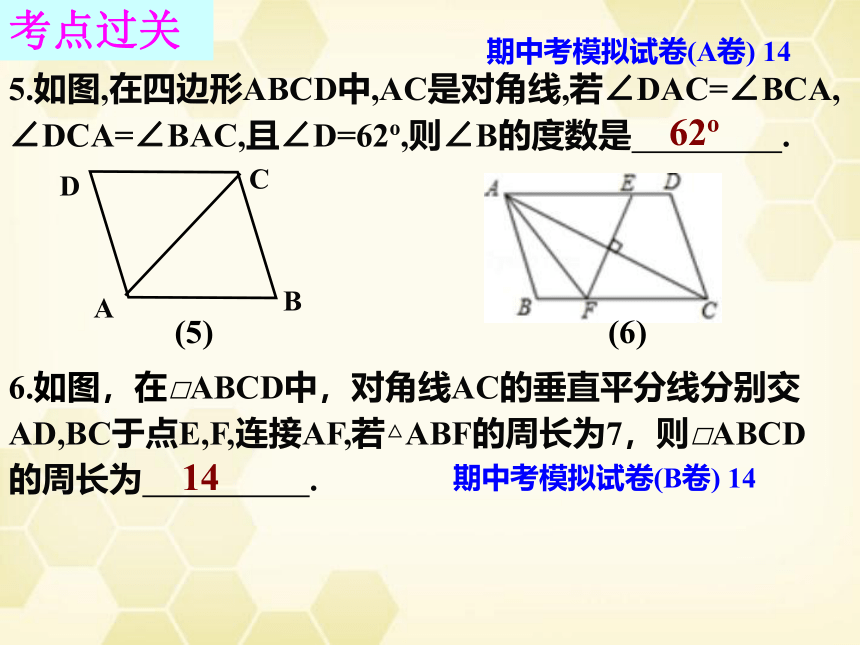
5.如图,在四边形ABCD中,AC是对角线,若∠DAC=∠BCA,
∠DCA=∠BAC,且∠D=62o,则∠B的度数是
.
A
B
C
D
期中考模拟试卷(A卷)
14
62o
6.如图,在□ABCD中,对角线AC的垂直平分线分别交
AD,BC于点E,F,连接AF,若△ABF的周长为7,则□ABCD
的周长为
.
(6)
(5)
期中考模拟试卷(B卷)
14
14
考点过关
7.如图,在□ABCD中,AB=5,AD=3,对角线AC与BD相交于
点O,若AC⊥BC,则BD的长为
.
期末考模拟试卷(B卷)
14
A
B
C
D
O
┍
E
考点过关
8.如图,在□ABCD中,点E,F分别在AD,BC上,且AE=CF,
EF,BD相交于点O,求证:OE=OF.
期末考模拟试卷(A卷)
19
证明:∵四边形ABCD是平行四边形,
∴
AD∥BC,AD=BC,∠EDO=∠FBO.
∵AE=CF,
∴
DE=BF,
又∵∠DOE=∠BOF,
∴△
DOE≌△BOF,
∴
OE=OF.
证明:连接BE、DF.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BEDF是平行四边形,
∴OF=OE.
考点过关
9.如图,已知□ABCD的周长为24,对角线AC,BD相交于点O,
△AOD与△AOB的周长之差为2,求AD,AB的长.
期末考模拟试卷(B卷)
20
解:∵四边形ABCD是平行四边形,
∴
OB=OD.
∵
△AOD与△AOB的周长之差为2,
∴
(OA+OD+AD)-(OA+OB+AB)=2,
即AD-AB=2……①.
∵
□ABCD的周长为24,
∴
AD+AB=12……②.
由①
②解得:AD=7,AB=5.
考点过关
考点二
平行四边形的性质和判定的综合应用
1.如图,在□ABCD中,DE平分∠ADC交AB于点G,交CB的
延长线于点E,BF平分∠ABC交AD的延长线于点F.
(1)若AD=5,AB=8,求GB的长;
(2)求证:∠E=∠F.
期末考模拟试卷(A卷)
22
(1)解:∵DE平分∠ADC,
∴∠1=∠2.
∵四边形ABCD是平行四边形,
∴
AB∥DC,
∴∠2=∠AGD,
∴∠1=∠AGD,
∴AD=AG=5,
∵AB=8,∴BG=8-5=3.
考点过关
1.如图,在□ABCD中,DE平分∠ADC交AB于点G,交CB的
延长线于点E,BF平分∠ABC交AD的延长线于点F.
(2)求证:∠E=∠F.
期末考模拟试卷(A卷)
22
(2)证明:∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,DC∥AB,AD∥BC.
∵
DE平分∠ADC,
BF平分∠ABC,
∴
∠2=
∠4.
∵
DC∥AB,
∴
∠2=∠AGD,
∴
∠4=∠AGD,
∴
DE∥FB.
∵AF∥CE,
∴
四边形BFDE是平行四边形,
∴
∠E=∠F.
考点过关
2.如图,在□ABCD中,AB=2AD,DE平分∠ADC,交AB于点E
,交CB的延长线于点F,EG∥AD交DC于点G.
(1)求证:四边形AEGD为菱形;
(2)若∠ADC=60o,AD=2,求DF的长.
期末考模拟试卷(B卷)
23
(1)证明:∵四边形ABCD是平行四边形,
∴
AB∥CD,
∴
∠AED=
∠GDE.
∵
AE∥DG,EG∥AD,
∴
四边形AEGD是平行四边形.
∵
DE平分∠ADC,
∴
∠ADE=∠GDE,
∴
∠ADE=∠GDE,
∴
AD=AE,
∴
四边形AEGD为菱形.
考点过关
2.如图,在□ABCD中,AB=2AD,DE平分∠ADC,交AB于点E
,交CB的延长线于点F,EG∥AD交DC于点G.
(2)若∠ADC=60o,AD=2,求DF的长.
期末考模拟试卷(B卷)
23
O
(2)连接AG交DE于点O.
∵四边形AEGD为菱形,
∴AD=DG,AG⊥DE.
∵∠ADC=60o,AD=2,
∴△ADG是等边三角形,
∴
AG=AD=2,
∵AD=AE,AB=2AD,
∴
AE=BE,
∵AD∥CF,
∴
∠ADE=∠F,∠DAE=∠FBE,
∴△
ADE≌△BFE,
∴
DE=EF,
小
结
与
复
习
第18章
平行四边形
几
何
语
言
文字叙述
对边平行
对边相等
对角相等
∴
AD=BC
,AB=DC.
∵
四边形ABCD是平行四边形,
∴
∠
A=∠C,∠
B=∠D.
∵
四边形ABCD是平行四边形,
一.平行四边形的性质
对角线互
相平分
∵
四边形ABCD是平行四边形,
∴
OA=OC,OB=OD.
∵
四边形ABCD是平行四边形,
∴
AD∥BC
,AB∥DC.
平行四边形是
中心对称图形.
A
B
C
D
O
要点梳理
几
何
语
言
文字叙述
两组对边相等
一组对边
平行且相等
∴四边形ABCD是平行四边形.
∵
AD=BC
,AB=DC,
∴
四边形ABCD是平行四边形.
∵
AB=DC,AB∥DC,
二、平行四边形的判定
对角线
互相平分
∴
四边形ABCD是平行四边形.
∵
OA=OC,OB=OD,
两组对边分别平行(定义)
∴四边形ABCD是平行四边形.
∵
AD∥BC
,AB∥DC,
平行线之间的距离处处相等.
要点梳理
A
B
C
D
O
考点过关
考点一
平行四边形的性质与判定
1.如图,在四边形ABCD中,AB=CD,对角线AC,BD相交于
点O,下列条件中,不能说明四边形ABCD是平行四边形的
是(
).
AD=BC
B.
AC=BD
C.
AB∥CD
D.
∠BAC=∠DCA
期末考模拟试卷(A卷)
2
B
2.在□ABCD中,AB=3
cm,BC=5
cm,对角线AC,BD相交于
O,则OA的取值范围是(
).
A.
1
cm
B.
2
cm
C.
2
cm
D.
3
cm
期中考模拟试卷(B卷)
4
A
3.如图,E是□ABCD边BC上的一点,且AB=BE,连接AE,
并延长AE与DC的延长线交于点F,若∠F=70o,则∠D的度数
是(
).
A.
30o
B.
40o
C.
50o
D.
70o
考点过关
B
期中考模拟试卷(B卷)
6
4.如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD于
点E,且AE=3,则AB的长为(
).
A.
2
B.
C.
3
D.
4
期中考模拟试卷(A卷)
8
C
考点过关
5.如图,在四边形ABCD中,AC是对角线,若∠DAC=∠BCA,
∠DCA=∠BAC,且∠D=62o,则∠B的度数是
.
A
B
C
D
期中考模拟试卷(A卷)
14
62o
6.如图,在□ABCD中,对角线AC的垂直平分线分别交
AD,BC于点E,F,连接AF,若△ABF的周长为7,则□ABCD
的周长为
.
(6)
(5)
期中考模拟试卷(B卷)
14
14
考点过关
7.如图,在□ABCD中,AB=5,AD=3,对角线AC与BD相交于
点O,若AC⊥BC,则BD的长为
.
期末考模拟试卷(B卷)
14
A
B
C
D
O
┍
E
考点过关
8.如图,在□ABCD中,点E,F分别在AD,BC上,且AE=CF,
EF,BD相交于点O,求证:OE=OF.
期末考模拟试卷(A卷)
19
证明:∵四边形ABCD是平行四边形,
∴
AD∥BC,AD=BC,∠EDO=∠FBO.
∵AE=CF,
∴
DE=BF,
又∵∠DOE=∠BOF,
∴△
DOE≌△BOF,
∴
OE=OF.
证明:连接BE、DF.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BEDF是平行四边形,
∴OF=OE.
考点过关
9.如图,已知□ABCD的周长为24,对角线AC,BD相交于点O,
△AOD与△AOB的周长之差为2,求AD,AB的长.
期末考模拟试卷(B卷)
20
解:∵四边形ABCD是平行四边形,
∴
OB=OD.
∵
△AOD与△AOB的周长之差为2,
∴
(OA+OD+AD)-(OA+OB+AB)=2,
即AD-AB=2……①.
∵
□ABCD的周长为24,
∴
AD+AB=12……②.
由①
②解得:AD=7,AB=5.
考点过关
考点二
平行四边形的性质和判定的综合应用
1.如图,在□ABCD中,DE平分∠ADC交AB于点G,交CB的
延长线于点E,BF平分∠ABC交AD的延长线于点F.
(1)若AD=5,AB=8,求GB的长;
(2)求证:∠E=∠F.
期末考模拟试卷(A卷)
22
(1)解:∵DE平分∠ADC,
∴∠1=∠2.
∵四边形ABCD是平行四边形,
∴
AB∥DC,
∴∠2=∠AGD,
∴∠1=∠AGD,
∴AD=AG=5,
∵AB=8,∴BG=8-5=3.
考点过关
1.如图,在□ABCD中,DE平分∠ADC交AB于点G,交CB的
延长线于点E,BF平分∠ABC交AD的延长线于点F.
(2)求证:∠E=∠F.
期末考模拟试卷(A卷)
22
(2)证明:∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,DC∥AB,AD∥BC.
∵
DE平分∠ADC,
BF平分∠ABC,
∴
∠2=
∠4.
∵
DC∥AB,
∴
∠2=∠AGD,
∴
∠4=∠AGD,
∴
DE∥FB.
∵AF∥CE,
∴
四边形BFDE是平行四边形,
∴
∠E=∠F.
考点过关
2.如图,在□ABCD中,AB=2AD,DE平分∠ADC,交AB于点E
,交CB的延长线于点F,EG∥AD交DC于点G.
(1)求证:四边形AEGD为菱形;
(2)若∠ADC=60o,AD=2,求DF的长.
期末考模拟试卷(B卷)
23
(1)证明:∵四边形ABCD是平行四边形,
∴
AB∥CD,
∴
∠AED=
∠GDE.
∵
AE∥DG,EG∥AD,
∴
四边形AEGD是平行四边形.
∵
DE平分∠ADC,
∴
∠ADE=∠GDE,
∴
∠ADE=∠GDE,
∴
AD=AE,
∴
四边形AEGD为菱形.
考点过关
2.如图,在□ABCD中,AB=2AD,DE平分∠ADC,交AB于点E
,交CB的延长线于点F,EG∥AD交DC于点G.
(2)若∠ADC=60o,AD=2,求DF的长.
期末考模拟试卷(B卷)
23
O
(2)连接AG交DE于点O.
∵四边形AEGD为菱形,
∴AD=DG,AG⊥DE.
∵∠ADC=60o,AD=2,
∴△ADG是等边三角形,
∴
AG=AD=2,
∵AD=AE,AB=2AD,
∴
AE=BE,
∵AD∥CF,
∴
∠ADE=∠F,∠DAE=∠FBE,
∴△
ADE≌△BFE,
∴
DE=EF,
