青岛五四制数学四年级下册7.4公倍数和最小公倍数 教案
文档属性
| 名称 | 青岛五四制数学四年级下册7.4公倍数和最小公倍数 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 793.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 00:00:00 | ||
图片预览




文档简介
《公倍数和最小公倍数》教学设计
【教学目标】
1.理解两个数的公倍数和最小公倍数的意义,初步了解两个数的公倍数和最小公倍数在现实生活中的应用。掌握求两个数最小公倍数的方法,培养学生用多种方法解决问题的能力。
2.经历公倍数和最小公倍数概念的产生过程和求两个数的最小公倍数的过程,体验观察思考,迁移发现,理解运用的学习方法。
3.在学习活动中,体验探索知识过程的乐趣,激发学习的兴趣,渗透集合的数学思想,培养严谨认真的学习态度。
【重点难点】
重点:理解两个数的公倍数和最小公倍数的意义,掌握求两个数的最小公倍数的方法。
难点:会用最小公倍数的知识解决实际问题
一、复习旧知
谈话:同学们,前面我们学习了因数与倍数,你能举例说一下什么是倍数吗?
【设计意图】随着学生回答,唤醒“倍数”的原有知识,是公倍数和最小公倍数的最近发展区。对一个数的倍数清晰明了,学习两个数的公倍数和最小公倍数也就水到渠成了,从倍数入手是教学活动的最佳起点。
二、探究新知
本环节解决两个问题:一是建立公倍数和最小公倍数的概念,二是探究两个数的公倍数和最小公倍数的方法。
(一)抢倍数——认识公倍数和最小公倍数
1、游戏
(1)从1----20这组数中,分别抢到2和3的倍数。
导语:同学们举了这么多关于倍数的例子,看来倍数的知识大家掌握的不错,我们进行一次抢倍数比赛好吗?
游戏规则:男同学抢2的倍数,女同学抢3的倍数,多抢、少抢都算错。
随着课件出示,男、女生抢2的倍数和3的倍数,分别填入集合图中。
游戏过程中,对于第一次出现2、3公有倍数6,男、女生同时抢时,提问抢6慢的一方:“这位同学,人家已经抢了6,为什么你也抢?”
提问理由:6既是2的倍数,也是3的倍数,这是本课学生第一次面对一个数同时是两个数的倍数,设计这样的追问,为下面引入公倍数的概念埋下伏笔。
(2)一个数倍数的个数是无限的
1----20中2和3的倍数抢完后,让学生继续说出2的倍数,问题引导:“能把2的倍数都说出来吗?为什么?”让学生清晰两个倍数集合图中要加上省略号,表示还有无数个倍数。
2、认识2和3的公倍数
总结思考:回想刚才抢倍数的过程,男、女同学同时抢的数有哪些?为什么?
像这样既是2的倍数也是3的倍数的数,我们称为2和3的公倍数。(板书课题:公倍数)
【设计意图】大家都抢的数,自然都有理由,老师的一个问题让孩子把理由描述出来,稍加整理就是一个新的知识点。抢倍数玩的高兴,主动获取知识学的高兴,孩子的生命状态是多么绚丽多姿。
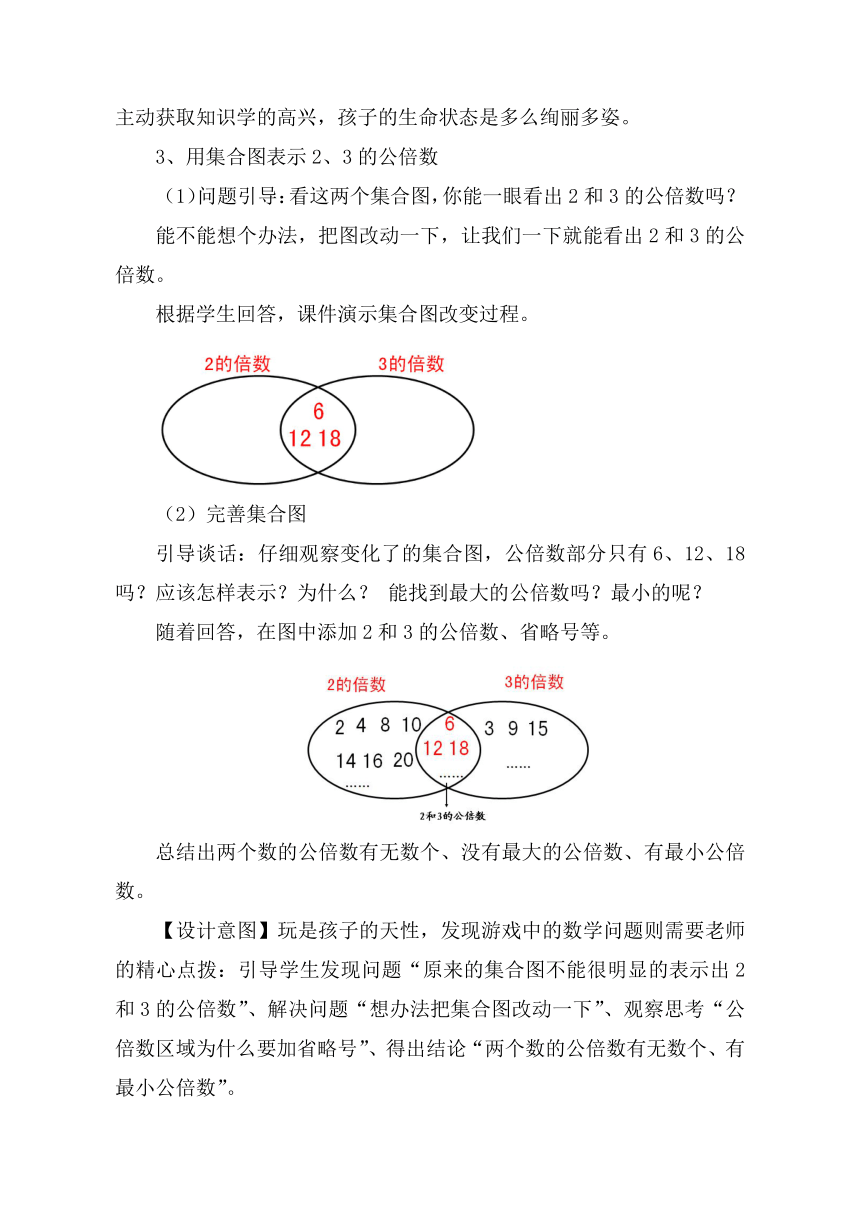
3、用集合图表示2、3的公倍数
(1)问题引导:看这两个集合图,你能一眼看出2和3的公倍数吗?
能不能想个办法,把图改动一下,让我们一下就能看出2和3的公倍数。
根据学生回答,课件演示集合图改变过程。
(2)完善集合图
引导谈话:仔细观察变化了的集合图,公倍数部分只有6、12、18吗?应该怎样表示?为什么? 能找到最大的公倍数吗?最小的呢?
随着回答,在图中添加2和3的公倍数、省略号等。
总结出两个数的公倍数有无数个、没有最大的公倍数、有最小公倍数。
【设计意图】玩是孩子的天性,发现游戏中的数学问题则需要老师的精心点拨:引导学生发现问题“原来的集合图不能很明显的表示出2和3的公倍数”、解决问题“想办法把集合图改动一下”、观察思考“公倍数区域为什么要加省略号”、得出结论“两个数的公倍数有无数个、有最小公倍数”。
4、提示课题:刚才我们通过抢倍数的游戏,学习了公倍数,也知道了最小公倍数,这节课我们就来研究“公倍数和最小公倍数”。
(二)探究公倍数和最小公倍数的方法
本环节分两个层次:一是运用已有知识求出12和18的公倍数和最小公倍数,二是看书自学,用短除法求最小公倍数。
1、运用已有知识找出12和18的公倍数和最小公倍数
谈话:我们已经知道了什么叫公倍数和最小公倍数,大家能不能想办法得出12和18的公倍数和最小公倍数?比比谁的方法多。
(1)学生独立思考,做到练习本上。
(2)全班交流。根据学生展示总结出下列方法:
A、列举法
12的倍数:12、24、36、48、60、72……
18的倍数:18、36、54、72……
12和18的公倍数:36、72……
12和18的最小公倍数:36
B、大数翻倍法
18的倍数:18、36、54、72……
12和18的公倍数:36、72……
12和18的最小公倍数:36
C、集合表示法
12的倍数 12和18的公倍数 18的倍数
学生交流方法时,做法不完善的,要及时进行补充。例如:三种方法很容易出现忽略省略号的现象,借机再次强调“一个数倍数的个数是无限的,两个数的公倍数的个数也是无限的”。
2、看书自学,用短除法求12和18的最小公倍数
(1)看书自学:我们用列举法、大数翻倍法、集合图法求出了12和18的公倍数和最小公倍数。大家回想一下,两个数的最大公因数通常我们用什么方法求的?求最小公倍数也可以用短除法。短除法求最小公倍数在课本106页上有祥细地介绍,相信大家通过自学一定能学会这种方法。
课件出示自学提纲:
(2)全班交流
a.自学结束后,提问自学提纲问题,同时板书短除式求12和18的最小公倍数。
b.观察板书短除式引导提问:谁能提醒大家用短除式求两个数的最小公倍数应注意什么问题?
这样既巩固了自学成果,又明晰了短除法求最小公倍数的方法及书写格式。
总结:短除法求最小公倍数要注意:用两个数的公因数做除数、除到公因数只有1为止、把除数和商相乘得到最小公倍数。
(3)练习:用短除法求最小公倍数 (男女同学各做一题)
18和24 8和36
全班订正时解决三个问题:
第一、方法巩固:引导学生提出问题,既巩固短除法求最小公倍数的方法,又培养学生的问题意识。
导语:这个同学做的对吗?可以向这个同学提出问题,考查一下他是不是真的理解这种方法了。
第二、区别用短除法求最小公倍数和最大公因数的不同
导语:观察短除式,18和24的最大公因数是多少?你是怎样知道的?
用短除式子求最大公因数和最小公倍数有什么不同点?
回答总结:求最大公因数是把除数相乘;求最小公倍数是把除数和商相乘。
第三、做短除法时除数的选择。
同时展示8和36最小公倍数的两种做法:
通过讨论明确:短除时既可以用较小的公因数去除,也可以用较大的公因数去除。
【设计意图】本环节的三个层次,分别承担着不同的教学内涵:第一层根据提纲自学。在原有短除式求最大公因数的基础上,根据自学提纲看书自学短除法求最小公倍数,可以培养学生的自学能力 ;第二层根据自学提纲板书短除式,形成求短除法求最小公倍数的数学模型;第三层练习用短除法求最小公倍数,并区别求最大公因数和最小公倍数的方法,加强新旧知识之间的联系。订正过程中针对除数的不同选择,让学生明白根据自己的实际情况可以用不同的公因数做除数,避免思维僵化。
三、公倍数和最小公倍数的实际应用
本环节设计了三个任务
导语:同学们,六一儿童节快到了,我们就用今天所学的知识完成三个任务,装扮美丽的校园,大家能完成吗?
任务一(课件出示):
小组探究:老师给大家准备了按这种剪纸规格缩小的模型,以组为单位摆一摆、想一想正方形展板的边长和剪纸的长和宽有什么关系?
学生分组探究后全班交流,得出结论:展板的边长是小长方形长和宽的公倍数,最短的边长就是长和宽的最小公倍数。
课件进一步演示展板的边长还可以是其它公倍数:
总结:动手操作可以帮助我们理解问题、解决问题,当我们在解决问题遇到困难的时候还可以画图、情境还原,这些都非常有利于帮助思考。
任务二:课件出示
学生独立解答,全班交流解决问题的方法:
一是短除法求9和6的最小公倍数,二是大数翻倍,9的2倍是9和6的最小公倍数。
总结:求两个数的最小公倍数的方法可以根据实际情况灵活选择。
任务三:(课件出示)
在学生独立思考的基础上,课件演示拼摆的过程,帮助学生理解正方体的棱长就是小长方体长、宽、高三个数的最小公倍数。
先摆成一行:
再摆成一层:
最后摆成一个正方体:
引伸谈话:求三个数的最小公倍数的方法我们下节课再来研究。
三个任务完成总结:公倍数和最小公倍数的知识可以解决一维空间——线的问题,二维空间——面的问题,也可以解决三维空间——体的问题。知识之间存在着千丝万缕的关系。
【设计意图】任务一,通过拼摆小长方形,理解求正方开展板最短的边长为什么是求长方形长和宽的最小公倍数。任务二,灵活运用求最小公倍数的方法解决实际问题。任务三,通过课件的直观演示,引伸下节课要研究的内容:求三个数的最小公倍数的计算方法。任务完成后的总结,是帮助学生沟通知识间的联系,将一维、二维、三维空间联结成网。
四、全课总结
1、学生谈收获——老师引导学生从知识、技能、情感等方面总结。
导语:同学们,一节课在我们玩游戏、看书自学、解决问题的过程中过去了,心情怎么样?在欢快的情绪中给自己留下了什么?
2、经典导引:老师想送给大家一句话,出自司马迁《史记 五帝本纪》“好学深思,心知其意”。意思是“喜好学习并能深入思考,心中领会其中的意义”。在数学学习中我们就要有这样的精神,不但要学会怎样做,还要多想想为什么这样做。短除法同学们学的很好了,想不想提出一个深层次的问题?手势指向除数和商相乘求最小公倍数,引导学生提出“求最小公倍数为什么要除数和商相乘”。
3、展示 “求最小公倍数为什么除数和商相乘”的道理,并布置“有兴趣的同学可以做进一步研究,数学实践活动课上与同学分享”。
【设计意图】本环节共分三个层次进行:一是让学生从情感、知识、技能多个方面整理总结本节课的收获;二是国学经典引入数学课堂,提高数学课的国学品味;三是培养学生“知其然,更要知其所以然”的意识,提出“为什么”这样做的问题,并用微课程加以解释,引导学生课后用自己的方法进一步研究。
【教学目标】
1.理解两个数的公倍数和最小公倍数的意义,初步了解两个数的公倍数和最小公倍数在现实生活中的应用。掌握求两个数最小公倍数的方法,培养学生用多种方法解决问题的能力。
2.经历公倍数和最小公倍数概念的产生过程和求两个数的最小公倍数的过程,体验观察思考,迁移发现,理解运用的学习方法。
3.在学习活动中,体验探索知识过程的乐趣,激发学习的兴趣,渗透集合的数学思想,培养严谨认真的学习态度。
【重点难点】
重点:理解两个数的公倍数和最小公倍数的意义,掌握求两个数的最小公倍数的方法。
难点:会用最小公倍数的知识解决实际问题
一、复习旧知
谈话:同学们,前面我们学习了因数与倍数,你能举例说一下什么是倍数吗?
【设计意图】随着学生回答,唤醒“倍数”的原有知识,是公倍数和最小公倍数的最近发展区。对一个数的倍数清晰明了,学习两个数的公倍数和最小公倍数也就水到渠成了,从倍数入手是教学活动的最佳起点。
二、探究新知
本环节解决两个问题:一是建立公倍数和最小公倍数的概念,二是探究两个数的公倍数和最小公倍数的方法。
(一)抢倍数——认识公倍数和最小公倍数
1、游戏
(1)从1----20这组数中,分别抢到2和3的倍数。
导语:同学们举了这么多关于倍数的例子,看来倍数的知识大家掌握的不错,我们进行一次抢倍数比赛好吗?
游戏规则:男同学抢2的倍数,女同学抢3的倍数,多抢、少抢都算错。
随着课件出示,男、女生抢2的倍数和3的倍数,分别填入集合图中。
游戏过程中,对于第一次出现2、3公有倍数6,男、女生同时抢时,提问抢6慢的一方:“这位同学,人家已经抢了6,为什么你也抢?”
提问理由:6既是2的倍数,也是3的倍数,这是本课学生第一次面对一个数同时是两个数的倍数,设计这样的追问,为下面引入公倍数的概念埋下伏笔。
(2)一个数倍数的个数是无限的
1----20中2和3的倍数抢完后,让学生继续说出2的倍数,问题引导:“能把2的倍数都说出来吗?为什么?”让学生清晰两个倍数集合图中要加上省略号,表示还有无数个倍数。
2、认识2和3的公倍数
总结思考:回想刚才抢倍数的过程,男、女同学同时抢的数有哪些?为什么?
像这样既是2的倍数也是3的倍数的数,我们称为2和3的公倍数。(板书课题:公倍数)
【设计意图】大家都抢的数,自然都有理由,老师的一个问题让孩子把理由描述出来,稍加整理就是一个新的知识点。抢倍数玩的高兴,主动获取知识学的高兴,孩子的生命状态是多么绚丽多姿。
3、用集合图表示2、3的公倍数
(1)问题引导:看这两个集合图,你能一眼看出2和3的公倍数吗?
能不能想个办法,把图改动一下,让我们一下就能看出2和3的公倍数。
根据学生回答,课件演示集合图改变过程。
(2)完善集合图
引导谈话:仔细观察变化了的集合图,公倍数部分只有6、12、18吗?应该怎样表示?为什么? 能找到最大的公倍数吗?最小的呢?
随着回答,在图中添加2和3的公倍数、省略号等。
总结出两个数的公倍数有无数个、没有最大的公倍数、有最小公倍数。
【设计意图】玩是孩子的天性,发现游戏中的数学问题则需要老师的精心点拨:引导学生发现问题“原来的集合图不能很明显的表示出2和3的公倍数”、解决问题“想办法把集合图改动一下”、观察思考“公倍数区域为什么要加省略号”、得出结论“两个数的公倍数有无数个、有最小公倍数”。
4、提示课题:刚才我们通过抢倍数的游戏,学习了公倍数,也知道了最小公倍数,这节课我们就来研究“公倍数和最小公倍数”。
(二)探究公倍数和最小公倍数的方法
本环节分两个层次:一是运用已有知识求出12和18的公倍数和最小公倍数,二是看书自学,用短除法求最小公倍数。
1、运用已有知识找出12和18的公倍数和最小公倍数
谈话:我们已经知道了什么叫公倍数和最小公倍数,大家能不能想办法得出12和18的公倍数和最小公倍数?比比谁的方法多。
(1)学生独立思考,做到练习本上。
(2)全班交流。根据学生展示总结出下列方法:
A、列举法
12的倍数:12、24、36、48、60、72……
18的倍数:18、36、54、72……
12和18的公倍数:36、72……
12和18的最小公倍数:36
B、大数翻倍法
18的倍数:18、36、54、72……
12和18的公倍数:36、72……
12和18的最小公倍数:36
C、集合表示法
12的倍数 12和18的公倍数 18的倍数
学生交流方法时,做法不完善的,要及时进行补充。例如:三种方法很容易出现忽略省略号的现象,借机再次强调“一个数倍数的个数是无限的,两个数的公倍数的个数也是无限的”。
2、看书自学,用短除法求12和18的最小公倍数
(1)看书自学:我们用列举法、大数翻倍法、集合图法求出了12和18的公倍数和最小公倍数。大家回想一下,两个数的最大公因数通常我们用什么方法求的?求最小公倍数也可以用短除法。短除法求最小公倍数在课本106页上有祥细地介绍,相信大家通过自学一定能学会这种方法。
课件出示自学提纲:
(2)全班交流
a.自学结束后,提问自学提纲问题,同时板书短除式求12和18的最小公倍数。
b.观察板书短除式引导提问:谁能提醒大家用短除式求两个数的最小公倍数应注意什么问题?
这样既巩固了自学成果,又明晰了短除法求最小公倍数的方法及书写格式。
总结:短除法求最小公倍数要注意:用两个数的公因数做除数、除到公因数只有1为止、把除数和商相乘得到最小公倍数。
(3)练习:用短除法求最小公倍数 (男女同学各做一题)
18和24 8和36
全班订正时解决三个问题:
第一、方法巩固:引导学生提出问题,既巩固短除法求最小公倍数的方法,又培养学生的问题意识。
导语:这个同学做的对吗?可以向这个同学提出问题,考查一下他是不是真的理解这种方法了。
第二、区别用短除法求最小公倍数和最大公因数的不同
导语:观察短除式,18和24的最大公因数是多少?你是怎样知道的?
用短除式子求最大公因数和最小公倍数有什么不同点?
回答总结:求最大公因数是把除数相乘;求最小公倍数是把除数和商相乘。
第三、做短除法时除数的选择。
同时展示8和36最小公倍数的两种做法:
通过讨论明确:短除时既可以用较小的公因数去除,也可以用较大的公因数去除。
【设计意图】本环节的三个层次,分别承担着不同的教学内涵:第一层根据提纲自学。在原有短除式求最大公因数的基础上,根据自学提纲看书自学短除法求最小公倍数,可以培养学生的自学能力 ;第二层根据自学提纲板书短除式,形成求短除法求最小公倍数的数学模型;第三层练习用短除法求最小公倍数,并区别求最大公因数和最小公倍数的方法,加强新旧知识之间的联系。订正过程中针对除数的不同选择,让学生明白根据自己的实际情况可以用不同的公因数做除数,避免思维僵化。
三、公倍数和最小公倍数的实际应用
本环节设计了三个任务
导语:同学们,六一儿童节快到了,我们就用今天所学的知识完成三个任务,装扮美丽的校园,大家能完成吗?
任务一(课件出示):
小组探究:老师给大家准备了按这种剪纸规格缩小的模型,以组为单位摆一摆、想一想正方形展板的边长和剪纸的长和宽有什么关系?
学生分组探究后全班交流,得出结论:展板的边长是小长方形长和宽的公倍数,最短的边长就是长和宽的最小公倍数。
课件进一步演示展板的边长还可以是其它公倍数:
总结:动手操作可以帮助我们理解问题、解决问题,当我们在解决问题遇到困难的时候还可以画图、情境还原,这些都非常有利于帮助思考。
任务二:课件出示
学生独立解答,全班交流解决问题的方法:
一是短除法求9和6的最小公倍数,二是大数翻倍,9的2倍是9和6的最小公倍数。
总结:求两个数的最小公倍数的方法可以根据实际情况灵活选择。
任务三:(课件出示)
在学生独立思考的基础上,课件演示拼摆的过程,帮助学生理解正方体的棱长就是小长方体长、宽、高三个数的最小公倍数。
先摆成一行:
再摆成一层:
最后摆成一个正方体:
引伸谈话:求三个数的最小公倍数的方法我们下节课再来研究。
三个任务完成总结:公倍数和最小公倍数的知识可以解决一维空间——线的问题,二维空间——面的问题,也可以解决三维空间——体的问题。知识之间存在着千丝万缕的关系。
【设计意图】任务一,通过拼摆小长方形,理解求正方开展板最短的边长为什么是求长方形长和宽的最小公倍数。任务二,灵活运用求最小公倍数的方法解决实际问题。任务三,通过课件的直观演示,引伸下节课要研究的内容:求三个数的最小公倍数的计算方法。任务完成后的总结,是帮助学生沟通知识间的联系,将一维、二维、三维空间联结成网。
四、全课总结
1、学生谈收获——老师引导学生从知识、技能、情感等方面总结。
导语:同学们,一节课在我们玩游戏、看书自学、解决问题的过程中过去了,心情怎么样?在欢快的情绪中给自己留下了什么?
2、经典导引:老师想送给大家一句话,出自司马迁《史记 五帝本纪》“好学深思,心知其意”。意思是“喜好学习并能深入思考,心中领会其中的意义”。在数学学习中我们就要有这样的精神,不但要学会怎样做,还要多想想为什么这样做。短除法同学们学的很好了,想不想提出一个深层次的问题?手势指向除数和商相乘求最小公倍数,引导学生提出“求最小公倍数为什么要除数和商相乘”。
3、展示 “求最小公倍数为什么除数和商相乘”的道理,并布置“有兴趣的同学可以做进一步研究,数学实践活动课上与同学分享”。
【设计意图】本环节共分三个层次进行:一是让学生从情感、知识、技能多个方面整理总结本节课的收获;二是国学经典引入数学课堂,提高数学课的国学品味;三是培养学生“知其然,更要知其所以然”的意识,提出“为什么”这样做的问题,并用微课程加以解释,引导学生课后用自己的方法进一步研究。
