5.1.2 轴对称变换同步练习(含解析)
文档属性
| 名称 | 5.1.2 轴对称变换同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 17:47:16 | ||
图片预览


文档简介
初中数学湘教版七年级下册5.1.2轴对称变换 同步练习
一、单选题
1.下列轴对称图形中,有4条对称轴的图形是( ??)
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
2.下列图形中,点P与点Q关于直线成轴对称的是(?? )
A.???????????????????????????????????????B.?
C.?????????????????????????????????????????D.?
3.如图所示的图形是轴对称图形,点A和点D,点B和点E是对应点.若∠A=50°,∠B=70°,则∠D+∠E的度数为(??? )
A.?100°????????????????????????????????????B.?110°????????????????????????????????????C.?120°????????????????????????????????????D.?130°
4.如图是P1、P2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7 , 判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?(?? )
A.?P2P3???????????????????????????????????B.?P4P5???????????????????????????????????C.?P7P8???????????????????????????????????D.?P8P9
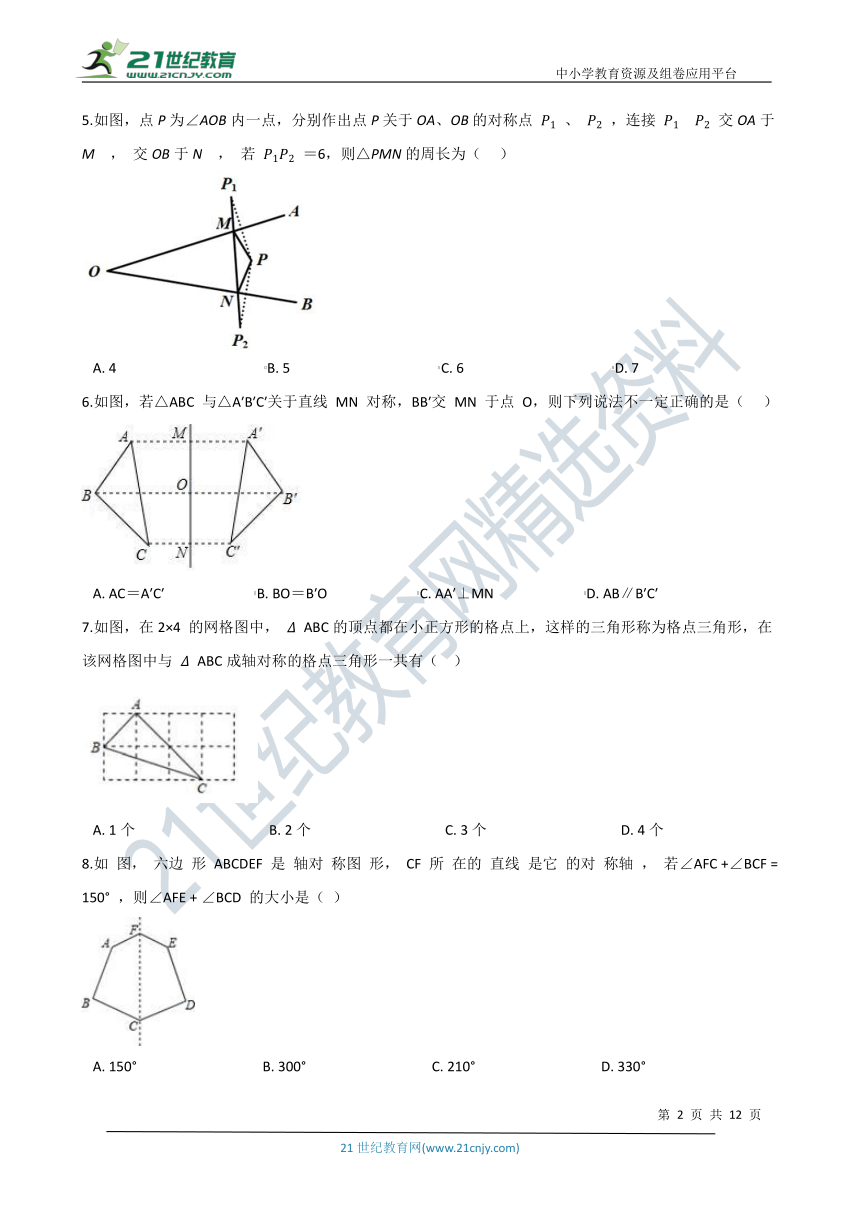
5.如图,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点 P1 、 P2 ,连接 P1 P2 交OA于M , 交OB于N , 若 P1P2 =6,则△PMN的周长为(??? )
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?7
6.如图,若△ABC 与△A′B′C′关于直线 MN 对称,BB′交 MN 于点 O,则下列说法不一定正确的是(??? )
A.?AC=A′C′??????????????????????????B.?BO=B′O??????????????????????????C.?AA′⊥MN??????????????????????????D.?AB∥B′C′
7.如图,在2×4 的网格图中, Δ ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在该网格图中与 Δ ABC成轴对称的格点三角形一共有(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
8.如 图, 六边 形 ABCDEF 是 轴对 称图 形, CF 所 在的 直线 是它 的对 称轴 , 若∠AFC +∠BCF = 150° ,则∠AFE + ∠BCD 的大小是( )
A.?150°????????????????????????????????????B.?300°????????????????????????????????????C.?210°????????????????????????????????????D.?330°
9.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AEAF根据图中标示的角度,则∠EAF的度数为( ??)
A.?113°????????????????????????????????????B.?124°????????????????????????????????????C.?129°????????????????????????????????????D.?134°
10.下列说法正确的是(?? )
A.?任何一个图形都有对称轴
B.?两个全等三角形一定关于某直线对称
C.?若△ABC与△A′B′C′成轴对称,则△ABC≌△A′B′C′
D.?点A,点B在直线1两旁,且AB与直线1交于点O,若AO=BO,则点A与点B关于直线l对称
二、填空题
11.在几何图形:等边三角形、正方形、正六边形和圆中,对称轴条数最多的是________.
12.如图是小明制作的风筝,为了平衡制成了轴对称图形,已知OC是对称轴,∠A=35?,∠BCO=30?,那么∠AOB=________.
13.已知两条互不平行的线段 AB 和 A'B' 关于直线L对称, AB 和 A'B' 所在的直线交于点P,下面四个结论:① AB=A'B' ;②点P在直线L上;③若A、 A' 是对应点,则直线L垂直平分线段 AA' ;④若B、 B' 是对应点,则 PB=PB' ,其中正确的是________(填序号).
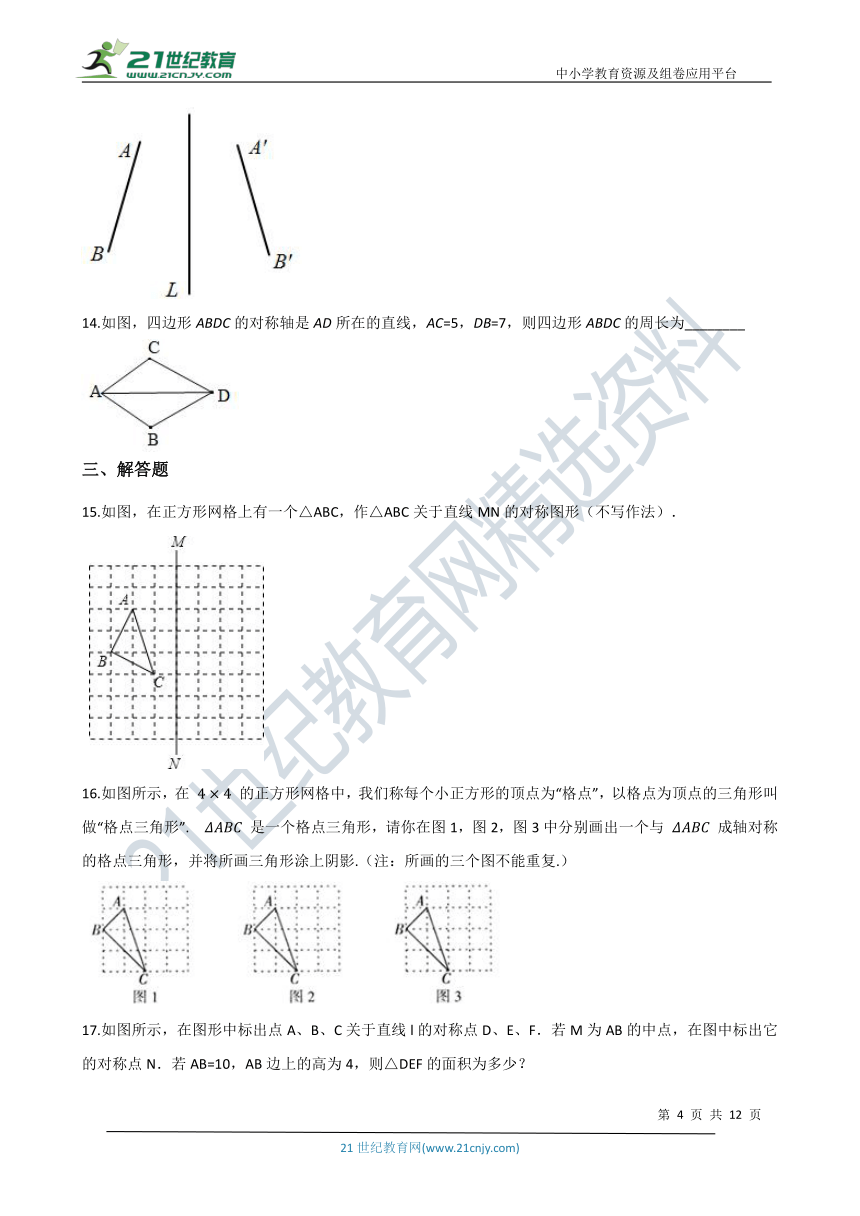
14.如图,四边形ABDC的对称轴是AD所在的直线,AC=5,DB=7,则四边形ABDC的周长为________
三、解答题
15.如图,在正方形网格上有一个△ABC,作△ABC关于直线MN的对称图形(不写作法).
16.如图所示,在 4×4 的正方形网格中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”. ΔABC 是一个格点三角形,请你在图1,图2,图3中分别画出一个与 ΔABC 成轴对称的格点三角形,并将所画三角形涂上阴影.(注:所画的三个图不能重复.)
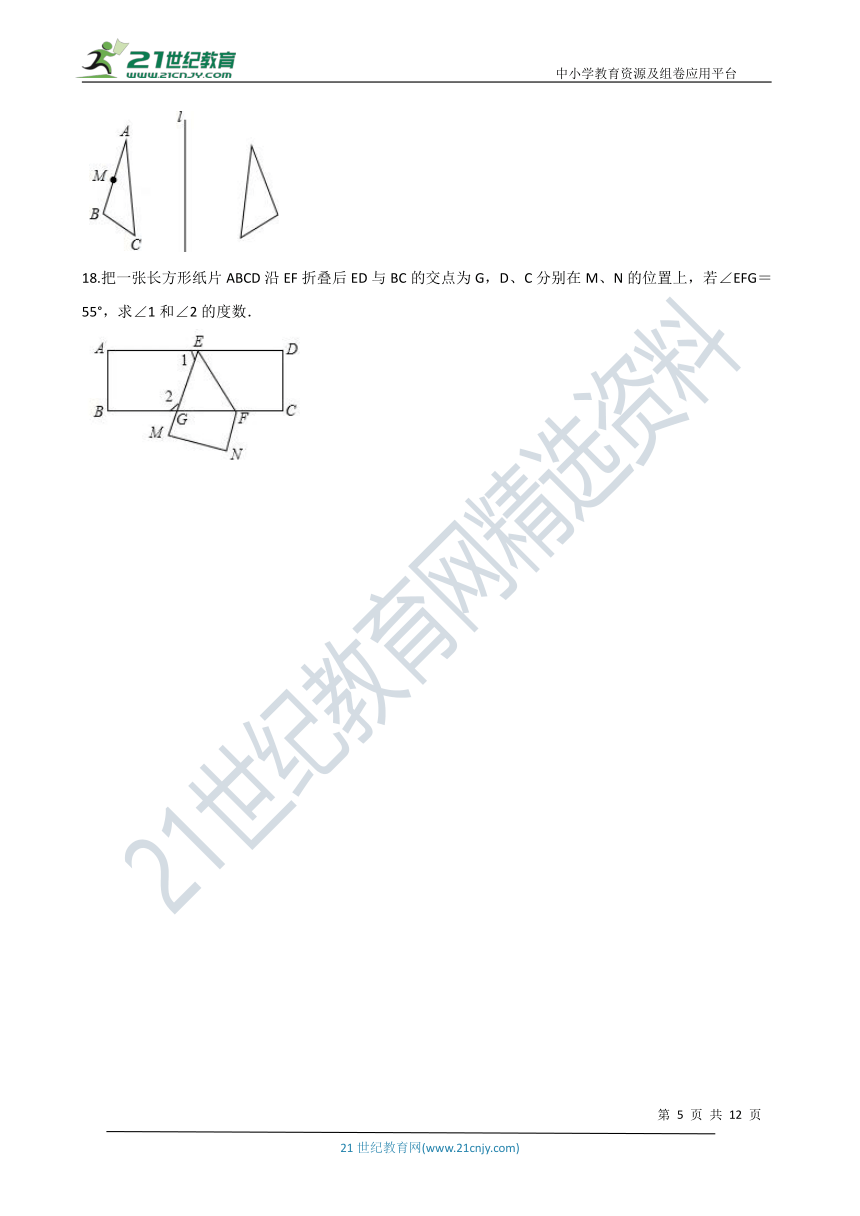
17.如图所示,在图形中标出点A、B、C关于直线l的对称点D、E、F.若M为AB的中点,在图中标出它的对称点N.若AB=10,AB边上的高为4,则△DEF的面积为多少?
18.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求∠1和∠2的度数.
答案解析部分
一、单选题
1. D
考点:轴对称的性质
解:A、是轴对称图形,有5条对称轴,故此选项不符合题意;
B、是轴对称图形,有3条对称轴,故此选项不符合题意;
C、是轴对称图形,有1条对称轴,故此选项不符合题意;
D、是轴对称图形,有4条对称轴,故此选项符合题意;
故答案为:D.
分析:根据轴对称的性质,判断得到答案即可。
2. D
考点:轴对称的性质
解:点P和点Q关于直线成轴对称,则直线和线段PQ的位置关系是:直线垂直平分PQ.
故答案为:D.
分析:点P与点Q关于直线成轴对称,根据轴对称的性质,有直线垂直平分PQ.
3. C
考点:轴对称的性质
解:∵该图形为轴对称图形,且点A与点D,点B和点E是对应点,
∴∠A=∠D=50°,∠B=∠E=70°
∴∠D+∠E=50°+70°=120°.
故答案选:C.
分析:根据轴对称图形的性质求解即可.
4. D
考点:轴对称的性质
解:由题意可得:当连接P2P3 , P4P5 , P7P8时,所形成的图形是轴对称图形,
当连接P8P9时,所形成的图形不是轴对称图形.
故答案为:D.
分析:把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形,根据定义即可一一判断得出答案.
5. C
考点:轴对称的性质
解:由轴对称的性质可得:OA垂直平分 P1P ,OB垂直平分 P2P ,
∴ P1M=PM , P2N=PN ,
∵ C△PMN=PM+PN+MN=P1M+P2N+MN=P1P2 , P1P2 =6,
∴ C△PMN=6 ;
故答案为:C.
分析:根据题意易得 P1M=PM , P2N=PN ,然后根据三角形的周长及线段的数量关系可求解.
6. D
考点:轴对称的性质
∵△ABC与△A′B′C′关于直线MN对称,
∴AC=A′C′,BO=B′O,AA′⊥MN,故A、B、C选项符合题意,AB∥B′C′不一定成立.
∴不一定正确的是选项D.
故答案为:D.
分析:根据轴对称图形的性质逐项判断即可。
7. C
考点:作图﹣轴对称
解:如图,
∴在该网格图中与ABC成轴对称的格点三角形一共有3个.
故答案为:C.
分析:利用轴对称的定义,画出符合题意的三角形即可。
8. B
考点:轴对称的性质
解:∵六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,∠AFC+∠BCF=150°,
∴∠AFC=∠EFC,∠BCF=∠DCF,
∴∠AFE+∠BCD=2(∠AFC+∠BCF)=300°.
故答案为:B
分析:直接利用轴对称图形的性质得出∠AFE+∠BCD=2(∠AFC+∠BCF),进而得出答案.
9. D
考点:轴对称的性质
解:连接AD,
∵D点为关于AB的对称点为E,D点为关于AC的对称点为F
∴∠EAB=∠BAD,∠FAC=∠CAD
∵∠B=62°,∠C=51°
∴∠BAC=∠BAD+∠BAC=180°-62°-51°=67°
∴∠EAF=2∠BAC=134°。
故答案为:D.
分析:连接AD,根据轴对称的性质,即可得到答案。
10. C
考点:轴对称的性质
A、轴对称图形才有对称轴,故不符合题意;
B、两个全等三角形一定关于某直线对称,由于位置关系不明确,不能符合题意判定,故不符合题意;
C、若△ABC与△A′B′C′成轴对称,则对应的线段、角都相等,则△ABC≌△A′B′C′,故符合题意;
D、点A,点B在直线1两旁,且AB与直线1交于点O,若AO=BO,则点A与点B关于直线l对称,由于位置关系不明确,不能符合题意判定,故不符合题意.
故答案为:C.
分析:全等三角形不一定是轴对称图形,只有轴对称图形才有对称轴,成轴对称的两个图形一定全等;若两点的连线垂直于某一天直线,且被直线平分,则这两点关于直线对称.
二、填空题
11. 圆
考点:轴对称的性质
由轴对称图形的性质可得:等边三角形对称轴的条数为3条,正方形的对称轴的条数为4条,正六边形对称轴的条数为6条,圆对称轴的条数为无数条,所以对称轴条数最多的是圆;
故答案为圆.
分析:根据等边三角形、正方形、正六边形和圆的对称轴可直接解答.
12. 130°
考点:轴对称的性质
依题意有∠AOB=2(∠A+∠ACO)=2(∠A+∠BCO)=130°.
即填:130°
分析:根据轴对称的性质可知,轴对称图形的两部分是全等的.
13. ①②③④
考点:轴对称的性质
由于不平行两直线关于直线L对称,因此对称轴一定处于交点处,如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称.
这样就得到了以下性质:
①如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
②类似地,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线;
③线段的垂直平分线上的点与这条线段的两个端点的距离相等;
④对称轴是到线段两端距离相等的点的集合.
于是①②③④都符合题意
故答案为:①②③④.
分析:轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线;线段垂直平分线的性质:线段的垂直平分线上的点与这条线段的两个端点的距离相等;据此逐一判断即可.
14. 24
考点:轴对称的性质
∵四边形ABDC的对称轴是AD所在的直线,AC=5,DB=7,
∴AB=AC=5,CD=BD=7,
∴四边形ABDC的周长=AC+CD+BD+AB=5+7+7+5=24.
故答案为:24.
分析:根据轴对称的性质进行解答即可.
三、解答题
15. 解:如图所示:△A′B′C′即为所求.
考点:作图﹣轴对称
分析:直接利用轴对称图形的性质得出对应点位置进而得出答案.
16. 答案不唯一,例如:
考点:作图﹣轴对称
分析:根据题意画出图形即可.
17. 解:如图所示,
∵AB=10,
∴DE=AB=10,
∴S△DEF= 12 ×10×4=20.
答:△DEF的面积是20.
考点:轴对称的性质,作图﹣轴对称
分析:根据轴对称的性质画出图形,由轴对称的性质可求出DE的长,再由三角形的面积公式进而可得出结论.
18. 解:∵AD∥BC?,
∴∠DEF=∠EFG=55°.
由对称性知∠GEF=∠DEF∠GEF=55°,??
∴∠GED=110°.
∵AD∥BC?,
∴∠2=∠GED=110°.
∴∠1=180°-110°=70°,
考点:平行线的性质,翻折变换(折叠问题)
分析:?由AD∥BC,可得∠DEF=∠EFG=55°.根据折叠的性质得出∠GEF=∠DEF,从而求出 ∠GED=110°,?由AD∥BC,可得∠2=∠GED=110°,根据两直线平行,同旁内角互补可得 ∠1=180°-∠2,据此计算即可.
一、单选题
1.下列轴对称图形中,有4条对称轴的图形是( ??)
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
2.下列图形中,点P与点Q关于直线成轴对称的是(?? )
A.???????????????????????????????????????B.?
C.?????????????????????????????????????????D.?
3.如图所示的图形是轴对称图形,点A和点D,点B和点E是对应点.若∠A=50°,∠B=70°,则∠D+∠E的度数为(??? )
A.?100°????????????????????????????????????B.?110°????????????????????????????????????C.?120°????????????????????????????????????D.?130°
4.如图是P1、P2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7 , 判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?(?? )
A.?P2P3???????????????????????????????????B.?P4P5???????????????????????????????????C.?P7P8???????????????????????????????????D.?P8P9
5.如图,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点 P1 、 P2 ,连接 P1 P2 交OA于M , 交OB于N , 若 P1P2 =6,则△PMN的周长为(??? )
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?7
6.如图,若△ABC 与△A′B′C′关于直线 MN 对称,BB′交 MN 于点 O,则下列说法不一定正确的是(??? )
A.?AC=A′C′??????????????????????????B.?BO=B′O??????????????????????????C.?AA′⊥MN??????????????????????????D.?AB∥B′C′
7.如图,在2×4 的网格图中, Δ ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在该网格图中与 Δ ABC成轴对称的格点三角形一共有(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
8.如 图, 六边 形 ABCDEF 是 轴对 称图 形, CF 所 在的 直线 是它 的对 称轴 , 若∠AFC +∠BCF = 150° ,则∠AFE + ∠BCD 的大小是( )
A.?150°????????????????????????????????????B.?300°????????????????????????????????????C.?210°????????????????????????????????????D.?330°
9.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AEAF根据图中标示的角度,则∠EAF的度数为( ??)
A.?113°????????????????????????????????????B.?124°????????????????????????????????????C.?129°????????????????????????????????????D.?134°
10.下列说法正确的是(?? )
A.?任何一个图形都有对称轴
B.?两个全等三角形一定关于某直线对称
C.?若△ABC与△A′B′C′成轴对称,则△ABC≌△A′B′C′
D.?点A,点B在直线1两旁,且AB与直线1交于点O,若AO=BO,则点A与点B关于直线l对称
二、填空题
11.在几何图形:等边三角形、正方形、正六边形和圆中,对称轴条数最多的是________.
12.如图是小明制作的风筝,为了平衡制成了轴对称图形,已知OC是对称轴,∠A=35?,∠BCO=30?,那么∠AOB=________.
13.已知两条互不平行的线段 AB 和 A'B' 关于直线L对称, AB 和 A'B' 所在的直线交于点P,下面四个结论:① AB=A'B' ;②点P在直线L上;③若A、 A' 是对应点,则直线L垂直平分线段 AA' ;④若B、 B' 是对应点,则 PB=PB' ,其中正确的是________(填序号).
14.如图,四边形ABDC的对称轴是AD所在的直线,AC=5,DB=7,则四边形ABDC的周长为________
三、解答题
15.如图,在正方形网格上有一个△ABC,作△ABC关于直线MN的对称图形(不写作法).
16.如图所示,在 4×4 的正方形网格中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”. ΔABC 是一个格点三角形,请你在图1,图2,图3中分别画出一个与 ΔABC 成轴对称的格点三角形,并将所画三角形涂上阴影.(注:所画的三个图不能重复.)
17.如图所示,在图形中标出点A、B、C关于直线l的对称点D、E、F.若M为AB的中点,在图中标出它的对称点N.若AB=10,AB边上的高为4,则△DEF的面积为多少?
18.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求∠1和∠2的度数.
答案解析部分
一、单选题
1. D
考点:轴对称的性质
解:A、是轴对称图形,有5条对称轴,故此选项不符合题意;
B、是轴对称图形,有3条对称轴,故此选项不符合题意;
C、是轴对称图形,有1条对称轴,故此选项不符合题意;
D、是轴对称图形,有4条对称轴,故此选项符合题意;
故答案为:D.
分析:根据轴对称的性质,判断得到答案即可。
2. D
考点:轴对称的性质
解:点P和点Q关于直线成轴对称,则直线和线段PQ的位置关系是:直线垂直平分PQ.
故答案为:D.
分析:点P与点Q关于直线成轴对称,根据轴对称的性质,有直线垂直平分PQ.
3. C
考点:轴对称的性质
解:∵该图形为轴对称图形,且点A与点D,点B和点E是对应点,
∴∠A=∠D=50°,∠B=∠E=70°
∴∠D+∠E=50°+70°=120°.
故答案选:C.
分析:根据轴对称图形的性质求解即可.
4. D
考点:轴对称的性质
解:由题意可得:当连接P2P3 , P4P5 , P7P8时,所形成的图形是轴对称图形,
当连接P8P9时,所形成的图形不是轴对称图形.
故答案为:D.
分析:把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形,根据定义即可一一判断得出答案.
5. C
考点:轴对称的性质
解:由轴对称的性质可得:OA垂直平分 P1P ,OB垂直平分 P2P ,
∴ P1M=PM , P2N=PN ,
∵ C△PMN=PM+PN+MN=P1M+P2N+MN=P1P2 , P1P2 =6,
∴ C△PMN=6 ;
故答案为:C.
分析:根据题意易得 P1M=PM , P2N=PN ,然后根据三角形的周长及线段的数量关系可求解.
6. D
考点:轴对称的性质
∵△ABC与△A′B′C′关于直线MN对称,
∴AC=A′C′,BO=B′O,AA′⊥MN,故A、B、C选项符合题意,AB∥B′C′不一定成立.
∴不一定正确的是选项D.
故答案为:D.
分析:根据轴对称图形的性质逐项判断即可。
7. C
考点:作图﹣轴对称
解:如图,
∴在该网格图中与ABC成轴对称的格点三角形一共有3个.
故答案为:C.
分析:利用轴对称的定义,画出符合题意的三角形即可。
8. B
考点:轴对称的性质
解:∵六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,∠AFC+∠BCF=150°,
∴∠AFC=∠EFC,∠BCF=∠DCF,
∴∠AFE+∠BCD=2(∠AFC+∠BCF)=300°.
故答案为:B
分析:直接利用轴对称图形的性质得出∠AFE+∠BCD=2(∠AFC+∠BCF),进而得出答案.
9. D
考点:轴对称的性质
解:连接AD,
∵D点为关于AB的对称点为E,D点为关于AC的对称点为F
∴∠EAB=∠BAD,∠FAC=∠CAD
∵∠B=62°,∠C=51°
∴∠BAC=∠BAD+∠BAC=180°-62°-51°=67°
∴∠EAF=2∠BAC=134°。
故答案为:D.
分析:连接AD,根据轴对称的性质,即可得到答案。
10. C
考点:轴对称的性质
A、轴对称图形才有对称轴,故不符合题意;
B、两个全等三角形一定关于某直线对称,由于位置关系不明确,不能符合题意判定,故不符合题意;
C、若△ABC与△A′B′C′成轴对称,则对应的线段、角都相等,则△ABC≌△A′B′C′,故符合题意;
D、点A,点B在直线1两旁,且AB与直线1交于点O,若AO=BO,则点A与点B关于直线l对称,由于位置关系不明确,不能符合题意判定,故不符合题意.
故答案为:C.
分析:全等三角形不一定是轴对称图形,只有轴对称图形才有对称轴,成轴对称的两个图形一定全等;若两点的连线垂直于某一天直线,且被直线平分,则这两点关于直线对称.
二、填空题
11. 圆
考点:轴对称的性质
由轴对称图形的性质可得:等边三角形对称轴的条数为3条,正方形的对称轴的条数为4条,正六边形对称轴的条数为6条,圆对称轴的条数为无数条,所以对称轴条数最多的是圆;
故答案为圆.
分析:根据等边三角形、正方形、正六边形和圆的对称轴可直接解答.
12. 130°
考点:轴对称的性质
依题意有∠AOB=2(∠A+∠ACO)=2(∠A+∠BCO)=130°.
即填:130°
分析:根据轴对称的性质可知,轴对称图形的两部分是全等的.
13. ①②③④
考点:轴对称的性质
由于不平行两直线关于直线L对称,因此对称轴一定处于交点处,如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称.
这样就得到了以下性质:
①如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
②类似地,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线;
③线段的垂直平分线上的点与这条线段的两个端点的距离相等;
④对称轴是到线段两端距离相等的点的集合.
于是①②③④都符合题意
故答案为:①②③④.
分析:轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线;线段垂直平分线的性质:线段的垂直平分线上的点与这条线段的两个端点的距离相等;据此逐一判断即可.
14. 24
考点:轴对称的性质
∵四边形ABDC的对称轴是AD所在的直线,AC=5,DB=7,
∴AB=AC=5,CD=BD=7,
∴四边形ABDC的周长=AC+CD+BD+AB=5+7+7+5=24.
故答案为:24.
分析:根据轴对称的性质进行解答即可.
三、解答题
15. 解:如图所示:△A′B′C′即为所求.
考点:作图﹣轴对称
分析:直接利用轴对称图形的性质得出对应点位置进而得出答案.
16. 答案不唯一,例如:
考点:作图﹣轴对称
分析:根据题意画出图形即可.
17. 解:如图所示,
∵AB=10,
∴DE=AB=10,
∴S△DEF= 12 ×10×4=20.
答:△DEF的面积是20.
考点:轴对称的性质,作图﹣轴对称
分析:根据轴对称的性质画出图形,由轴对称的性质可求出DE的长,再由三角形的面积公式进而可得出结论.
18. 解:∵AD∥BC?,
∴∠DEF=∠EFG=55°.
由对称性知∠GEF=∠DEF∠GEF=55°,??
∴∠GED=110°.
∵AD∥BC?,
∴∠2=∠GED=110°.
∴∠1=180°-110°=70°,
考点:平行线的性质,翻折变换(折叠问题)
分析:?由AD∥BC,可得∠DEF=∠EFG=55°.根据折叠的性质得出∠GEF=∠DEF,从而求出 ∠GED=110°,?由AD∥BC,可得∠2=∠GED=110°,根据两直线平行,同旁内角互补可得 ∠1=180°-∠2,据此计算即可.
