5.2 旋转同步练习(含解析)
图片预览


文档简介
初中数学湘教版七年级下册5.2旋转 同步练习
一、单选题
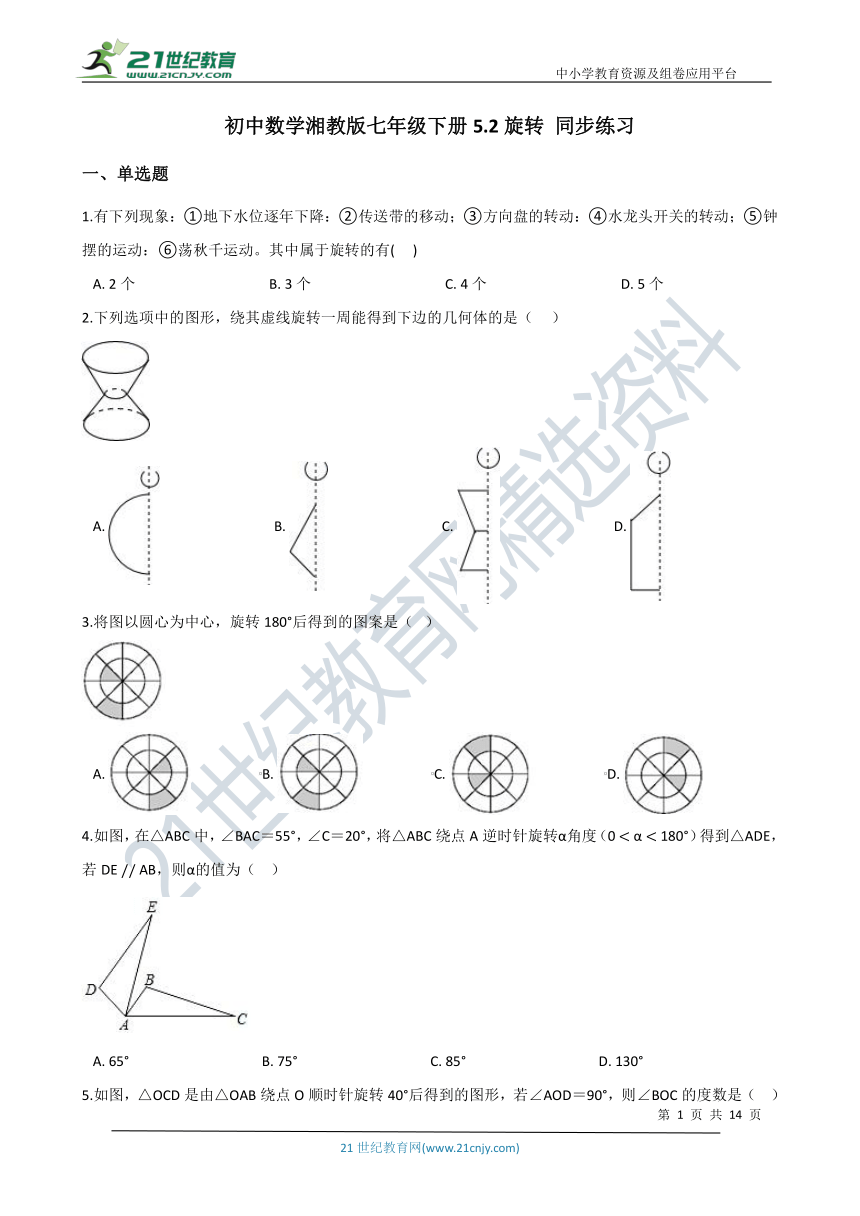
1.有下列现象:①地下水位逐年下降:②传送带的移动;③方向盘的转动:④水龙头开关的转动;⑤钟摆的运动:⑥荡秋千运动。其中属于旋转的有(??? )
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
2.下列选项中的图形,绕其虚线旋转一周能得到下边的几何体的是(??? )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
3.将图以圆心为中心,旋转180°后得到的图案是(? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
4.如图,在△ABC中,∠BAC=55°,∠C=20°,将△ABC绕点A逆时针旋转α角度(0 < α < 180°)得到△ADE,若DE // AB,则α的值为(?? )
A.?65°??????????????????????????????????????B.?75°??????????????????????????????????????C.?85°??????????????????????????????????????D.?130°
5.如图,△OCD是由△OAB绕点O顺时针旋转40°后得到的图形,若∠AOD=90°,则∠BOC的度数是(?? )
A.?5°???????????????????????????????????????B.?10°???????????????????????????????????????C.?15°???????????????????????????????????????D.?20°
6.如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转 72° 后,能与原图形完全重合的是(??? )
A.??????????????????????B.??????????????????????C.??????????????????????D.?
7.如图,五角星的五个顶点等分圆周,把这个图形顺时针旋转,一定的角度后能与自身重合,那么这个角度至少是 ( ???)
A.?60°???????????????????????????????????????B.?72°???????????????????????????????????????C.?75°???????????????????????????????????????D.?90°
8.如图,将△ABC绕点C顺时针旋转得到△DEC , 使点A的对应点D恰好落在边AB上,点B的对应点为E , 连接BE , 下列四个结论:
①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC;
其中一定正确的是(?? )
A.?①②????????????????????????????????????B.?②③????????????????????????????????????C.?③④????????????????????????????????????D.?②③④
9.在图形的旋转中,下列说法错误的是( ???)
A.?图形上的每一点到旋转中心的距离都相等???????????B.?图形上的每一点转动的角度都相同
C.?图形上可能存在不动的点????????????????????????????????????D.?旋转前和旋转后的图形全等
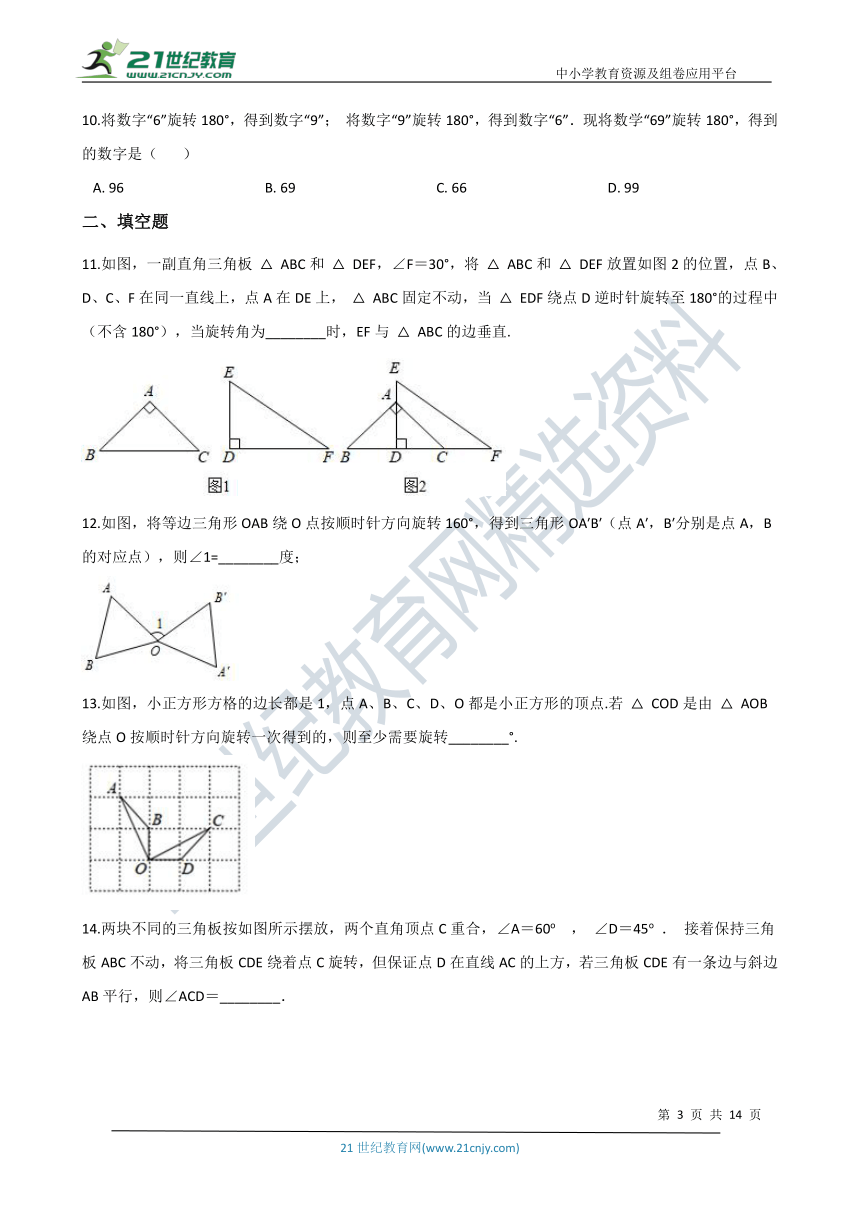
10.将数字“6”旋转180°,得到数字“9”; 将数字“9”旋转180°,得到数字“6”.现将数学“69”旋转180°,得到的数字是(? ????)
A.?96?????????????????????????????????????????B.?69?????????????????????????????????????????C.?66?????????????????????????????????????????D.?99
二、填空题
11.如图,一副直角三角板 △ ABC和 △ DEF,∠F=30°,将 △ ABC和 △ DEF放置如图2的位置,点B、D、C、F在同一直线上,点A在DE上, △ ABC固定不动,当 △ EDF绕点D逆时针旋转至180°的过程中(不含180°),当旋转角为________时,EF与 △ ABC的边垂直.
12.如图,将等边三角形OAB绕O点按顺时针方向旋转160°,得到三角形OA′B′(点A′,B′分别是点A,B的对应点),则∠1=________度;
13.如图,小正方形方格的边长都是1,点A、B、C、D、O都是小正方形的顶点.若 △ COD是由 △ AOB绕点O按顺时针方向旋转一次得到的,则至少需要旋转________°.
14.两块不同的三角板按如图所示摆放,两个直角顶点C重合,∠A=60o , ∠D=45o . 接着保持三角板ABC不动,将三角板CDE绕着点C旋转,但保证点D在直线AC的上方,若三角板CDE有一条边与斜边AB平行,则∠ACD=________.
三、解答题
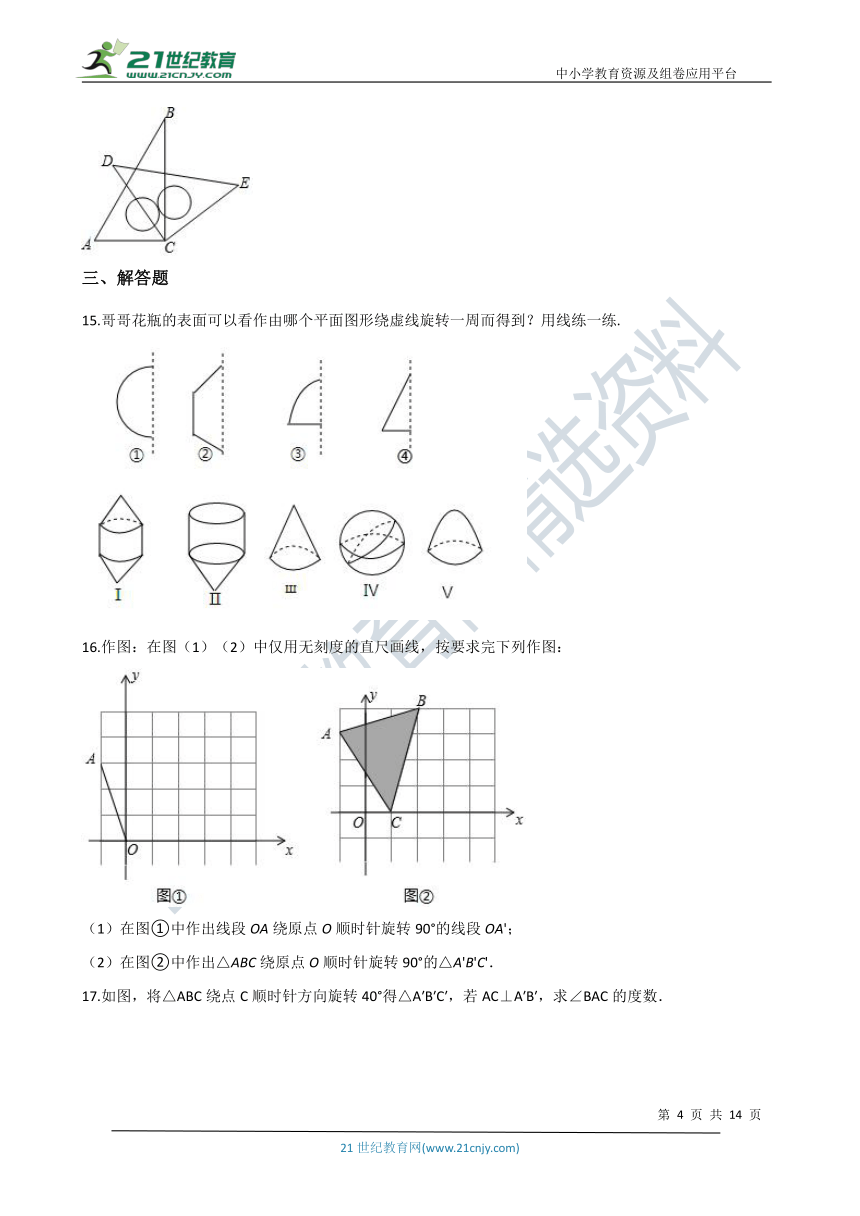
15.哥哥花瓶的表面可以看作由哪个平面图形绕虚线旋转一周而得到?用线练一练.
16.作图:在图(1)(2)中仅用无刻度的直尺画线,按要求完下列作图:
(1)在图①中作出线段OA绕原点O顺时针旋转90°的线段OA';
(2)在图②中作出△ABC绕原点O顺时针旋转90°的△A'B'C'.
17.如图,将△ABC绕点C顺时针方向旋转40°得△A′B′C′,若AC⊥A′B′,求∠BAC的度数.
18.如图,△ABC逆时针旋转一定角度后与△ADE重合,且点C在AD上.
(1)指出旋转中心;
(2)若∠B=21°,∠ACB=26°,求出旋转的度数;
(3)岩AB=5,CD=3,则AE的长是多少?为什么?
19.如图,点E为正方形ABCD的边AB上一点,AB=12,AE=5,将△DAE旋转后能与△DCF重合。
(1)旋转中心是哪一点?
(2)旋转的最小角是多少度?
(3)求四边形DEBF的周长和面积。
答案解析部分
一、单选题
1. C
考点:生活中的平移现象,生活中的旋转现象
解:③④⑤⑥属于旋转,共有4个.
故答案为:C.
分析:根据平移和旋转的定义对各运动进行分析,即可找出其中的旋转运动.
2. C
考点:图形的旋转,生活中的旋转现象
解:A. 旋转一周为球体,不符合题意;
B. 旋转一周为两个圆锥结合体,不符合题意;
C. 旋转一周可得本题的几何体,符合题意;
D. 旋转一周为圆锥和圆柱的结合体,不符合题意.
故答案为:C.
分析:根据面动成体判断出各个选项旋转得到的立体图即可得出结论.
3. D
考点:图形的旋转
将 以圆心为中心,旋转180°后得到的图案是 ,
故答案为:D.
分析:根据旋转的性质对每个选项一一判断即可。
4. B
考点:旋转的性质
解:∵在△ABC中,∠BAC=55°,∠C=20°,
∴∠ABC=180°﹣∠BAC﹣∠C═180°﹣55°﹣20°=105°,
∵将△ABC绕点A逆时针旋转α角度(0<α<180°)得到△ADE,
∴∠ADE=∠ABC=105°,
∵DE∥AB,
∴∠ADE+∠DAB=180°,
∴∠DAB=180°﹣∠ADE=75°
∴旋转角α的度数是75°,
故答案为:B.
分析:根据三角形内角和∠ABC=180°﹣∠BAC﹣∠C=105°,利用旋转的性质可得∠ADE=∠ABC=105°,根据平行线的性质可得∠DAB=180°﹣∠ADE=75°.
5. B
考点:旋转的性质
解:由题意得,∠AOC=40°,∠BOD=40°,
又∠AOD=90°,
∴∠BOC=90°-40°-40°=10°,
故答案为:B.
分析:利用旋转的性质可求出∠AOC=∠BOD=40°,再利用∠AOD=90°,可求出∠BOC的度数.
6. D
考点:旋转对称图形
解:A图形顺时针旋转120°后,能与原图形完全重合,A不正确;
B图形顺时针旋转90°后,能与原图形完全重合,B不正确;
C图形顺时针旋转180°后,能与原图形完全重合,C不正确;
D图形顺时针旋转72°后,能与原图形完全重合,D正确;
故选:D.
分析:利用正多边形的每一个内角度数的计算方法,分别求出选项A,B,D中的多边形的一个内角的度数,由此可作出判断.
7. B
考点:图形的旋转
360°÷5=72°
故至少旋转72°后能够重合
故答案为:B
分析:用圆周角除5得到每个顶点之间的角度,即为旋转后重合的角度
8. C
考点:旋转的性质
解:∵旋转,
∴ AC=DC ,
但是旋转角不一定是 60° ,
∴ △ACD 不一定是等边三角形,
∴ AC=AD 不一定成立,即①不一定符合题意;
∵旋转,
∴ BC=EC ,故③符合题意;
∵旋转,
∴ ∠ACD=∠BCE ,
∵等腰三角形ACD和等腰三角形BCE的顶角相等,
∴它们的底角也相等,即 ∠A=∠EBC ,故④符合题意;
∵ ∠A+∠ABC=90° 不一定成立,
∴ ∠EBC+∠ABC=90° 不一定成立,
∴ AB⊥EB 不一定成立,即②不一定符合题意.
故答案为:C.
分析:根据旋转的性质,得到对应边相等,旋转角相等,从而去判断命题的正确性.
9. A
考点:旋转的性质
解:A.图形上的对应点,到旋转中心的距离相等,说法错误;
B.图形上的每一点转动的角度都相同,都等于 旋转角,说法正确;
C.当图形上的点为旋转中心时,旋转中心不动,说法正确;
D.旋转前后,两个图形全等。
故答案为:A.
分析:根据旋转的性质,分别进行判断得到答案即可。
10. B
考点:旋转的性质
解:根据旋转的性质,“69”旋转180°得到的数字为“69”
故答案为:B.
分析:根据旋转的性质,即可得到答案。
二、填空题
11. 120°
考点:旋转的性质
解:当旋转角为120°时,EF⊥BC.
理由如下:∵△DEF绕点D逆时针旋转120°,
∴∠BDE=30°,
∵∠E=60°,
∴∠E+∠BDE=90°,
∴EF⊥BC,
故答案为120°.
分析:由旋转的性质可得当旋转角为120°时,∠BDE=30°,根据∠E+∠BDE=90°,可得EF⊥BC.
12. 100
考点:旋转的性质
解:∵将等边三角形OAB绕O点按顺时针方向旋转160°,得到三角形OA'B',
∴ ∠BOB'=160° , ∠AOB=60° ,
∴ ∠1=∠BOB'-∠AOB=100° ,
故答案为:100.
分析:根据旋转的性质,可得 ∠BOB'=160° ,再根据等边三角形OAB中 ∠AOB=60° ,即可求解.
13. 90
考点:旋转的性质
解:∵△COD是由△AOB绕点O按顺时针方向旋转而得,
∴OB=OD,
∴旋转的角度是∠BOD的大小,
∵∠BOD=90°,
∴旋转的角度为90°,
故答案为: 90.
分析:由△COD是由△AOB绕点O按顺时针方向旋转而得到,再结合已知图形可知旋转的角度是∠BOD的大小,然后由图形即可求得答案
14. 30°或120°或165°
考点:图形的旋转,旋转的性质
解:如图,CD∥AB,∠BCD=∠B=30°,
∠ACD=∠ACB+∠BCD=90°+30°=120°;
如图,DE∥AB时,延长EC交AB于F,
则∠AFC=∠E=45°,
在 △ACF 中,∠ACF=180°﹣∠A﹣∠AFC,
=180°﹣60°﹣45°=75°,
∵∠DCE=90°, ?
∴∠DCF=90°, ?
∴∠ACD= ∠ACF+∠DCF=75°+90°=165° ;
如图,当 CE//AB 时,
∴∠A=∠ACE=60°, ?
∴ ?∠ACD= ∠DCE-∠ACE= 30°,
故答案为:30°或120°或165°.
分析:分CE、DE、CD与AB平行分别作出图形,再根据平行线的性质求解即可。
三、解答题
15. 解:如图所示:
考点:图形的旋转
分析:根据“面动成体”的原理,结合图形特征进行旋转,判断出旋转后的立体图形即可.
16. (1)解:如图1,OA′为所作;
(2)解:如图2,△A'B'C'为所作.
考点:旋转的性质,作图﹣旋转
分析:(1)利用网格特点和旋转的性质,画出点A的对应点A′即可;(2)利用网格特点和旋转的性质,画出点A的对应点A′、B点的对应点B′、点C的对应点C′,再顺次连接即可.
17. 解:∵△ABC绕点C顺时针方向旋转40?得△A′B′C′,
∴∠ACA′=40?,∠A=∠A′,
∵AC⊥A′B′,
∴∠A′=90°﹣40°=50°,
∴∠BAC=50°
考点:旋转的性质
分析:根据“旋转前后的图形全等”可求解。
18. (1)旋转中心为点A
(2)解:∵∠B=21°,∠ACB=26°,
∴∠BAC=180°﹣21°﹣26°=133°,
∴旋转的度数为133°
(3)解:由旋转性质知:AE=AC,AD=AB,
∴AE=AB﹣CD=2.
考点:旋转的性质
分析:(1)根据旋转的概念,得到△ABC各个顶点的对应点,再顺次连接起来,即可;
(2)根据三角形内角和定理,得到∠BAC的度数,即可求解;
(3)根据旋转的性质,得到对应边相等,进而即可求解.
19. (1)解:点D
(2)解:90°
(3)解:由旋转可得DE=DF=13,BE=AB-AE=7,BF=BC+CF=17
所以,四边形D肋F的周K=13+1 3+7+17=50
四边形DEBF的面积=正方形ABCD的面积=12×12=144
考点:旋转的性质
分析:(1)观察图形,根据旋转的性质即可确定出旋转中心;
(2)找出对应线段的夹角即为旋转角,如AD和CD之间的夹角,根据正方形的性质求解;
(3)根据旋转的性质可得AE=CF,DE=DF,根据勾股定理计算出DE的长,进而可求出四边形DEBF的周长;
根据旋转的性质可得S△ADE=S△CDF , 即可得到四边形DEBF等于正方形ABCD的面积.
一、单选题
1.有下列现象:①地下水位逐年下降:②传送带的移动;③方向盘的转动:④水龙头开关的转动;⑤钟摆的运动:⑥荡秋千运动。其中属于旋转的有(??? )
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
2.下列选项中的图形,绕其虚线旋转一周能得到下边的几何体的是(??? )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
3.将图以圆心为中心,旋转180°后得到的图案是(? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
4.如图,在△ABC中,∠BAC=55°,∠C=20°,将△ABC绕点A逆时针旋转α角度(0 < α < 180°)得到△ADE,若DE // AB,则α的值为(?? )
A.?65°??????????????????????????????????????B.?75°??????????????????????????????????????C.?85°??????????????????????????????????????D.?130°
5.如图,△OCD是由△OAB绕点O顺时针旋转40°后得到的图形,若∠AOD=90°,则∠BOC的度数是(?? )
A.?5°???????????????????????????????????????B.?10°???????????????????????????????????????C.?15°???????????????????????????????????????D.?20°
6.如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转 72° 后,能与原图形完全重合的是(??? )
A.??????????????????????B.??????????????????????C.??????????????????????D.?
7.如图,五角星的五个顶点等分圆周,把这个图形顺时针旋转,一定的角度后能与自身重合,那么这个角度至少是 ( ???)
A.?60°???????????????????????????????????????B.?72°???????????????????????????????????????C.?75°???????????????????????????????????????D.?90°
8.如图,将△ABC绕点C顺时针旋转得到△DEC , 使点A的对应点D恰好落在边AB上,点B的对应点为E , 连接BE , 下列四个结论:
①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC;
其中一定正确的是(?? )
A.?①②????????????????????????????????????B.?②③????????????????????????????????????C.?③④????????????????????????????????????D.?②③④
9.在图形的旋转中,下列说法错误的是( ???)
A.?图形上的每一点到旋转中心的距离都相等???????????B.?图形上的每一点转动的角度都相同
C.?图形上可能存在不动的点????????????????????????????????????D.?旋转前和旋转后的图形全等
10.将数字“6”旋转180°,得到数字“9”; 将数字“9”旋转180°,得到数字“6”.现将数学“69”旋转180°,得到的数字是(? ????)
A.?96?????????????????????????????????????????B.?69?????????????????????????????????????????C.?66?????????????????????????????????????????D.?99
二、填空题
11.如图,一副直角三角板 △ ABC和 △ DEF,∠F=30°,将 △ ABC和 △ DEF放置如图2的位置,点B、D、C、F在同一直线上,点A在DE上, △ ABC固定不动,当 △ EDF绕点D逆时针旋转至180°的过程中(不含180°),当旋转角为________时,EF与 △ ABC的边垂直.
12.如图,将等边三角形OAB绕O点按顺时针方向旋转160°,得到三角形OA′B′(点A′,B′分别是点A,B的对应点),则∠1=________度;
13.如图,小正方形方格的边长都是1,点A、B、C、D、O都是小正方形的顶点.若 △ COD是由 △ AOB绕点O按顺时针方向旋转一次得到的,则至少需要旋转________°.
14.两块不同的三角板按如图所示摆放,两个直角顶点C重合,∠A=60o , ∠D=45o . 接着保持三角板ABC不动,将三角板CDE绕着点C旋转,但保证点D在直线AC的上方,若三角板CDE有一条边与斜边AB平行,则∠ACD=________.
三、解答题
15.哥哥花瓶的表面可以看作由哪个平面图形绕虚线旋转一周而得到?用线练一练.
16.作图:在图(1)(2)中仅用无刻度的直尺画线,按要求完下列作图:
(1)在图①中作出线段OA绕原点O顺时针旋转90°的线段OA';
(2)在图②中作出△ABC绕原点O顺时针旋转90°的△A'B'C'.
17.如图,将△ABC绕点C顺时针方向旋转40°得△A′B′C′,若AC⊥A′B′,求∠BAC的度数.
18.如图,△ABC逆时针旋转一定角度后与△ADE重合,且点C在AD上.
(1)指出旋转中心;
(2)若∠B=21°,∠ACB=26°,求出旋转的度数;
(3)岩AB=5,CD=3,则AE的长是多少?为什么?
19.如图,点E为正方形ABCD的边AB上一点,AB=12,AE=5,将△DAE旋转后能与△DCF重合。
(1)旋转中心是哪一点?
(2)旋转的最小角是多少度?
(3)求四边形DEBF的周长和面积。
答案解析部分
一、单选题
1. C
考点:生活中的平移现象,生活中的旋转现象
解:③④⑤⑥属于旋转,共有4个.
故答案为:C.
分析:根据平移和旋转的定义对各运动进行分析,即可找出其中的旋转运动.
2. C
考点:图形的旋转,生活中的旋转现象
解:A. 旋转一周为球体,不符合题意;
B. 旋转一周为两个圆锥结合体,不符合题意;
C. 旋转一周可得本题的几何体,符合题意;
D. 旋转一周为圆锥和圆柱的结合体,不符合题意.
故答案为:C.
分析:根据面动成体判断出各个选项旋转得到的立体图即可得出结论.
3. D
考点:图形的旋转
将 以圆心为中心,旋转180°后得到的图案是 ,
故答案为:D.
分析:根据旋转的性质对每个选项一一判断即可。
4. B
考点:旋转的性质
解:∵在△ABC中,∠BAC=55°,∠C=20°,
∴∠ABC=180°﹣∠BAC﹣∠C═180°﹣55°﹣20°=105°,
∵将△ABC绕点A逆时针旋转α角度(0<α<180°)得到△ADE,
∴∠ADE=∠ABC=105°,
∵DE∥AB,
∴∠ADE+∠DAB=180°,
∴∠DAB=180°﹣∠ADE=75°
∴旋转角α的度数是75°,
故答案为:B.
分析:根据三角形内角和∠ABC=180°﹣∠BAC﹣∠C=105°,利用旋转的性质可得∠ADE=∠ABC=105°,根据平行线的性质可得∠DAB=180°﹣∠ADE=75°.
5. B
考点:旋转的性质
解:由题意得,∠AOC=40°,∠BOD=40°,
又∠AOD=90°,
∴∠BOC=90°-40°-40°=10°,
故答案为:B.
分析:利用旋转的性质可求出∠AOC=∠BOD=40°,再利用∠AOD=90°,可求出∠BOC的度数.
6. D
考点:旋转对称图形
解:A图形顺时针旋转120°后,能与原图形完全重合,A不正确;
B图形顺时针旋转90°后,能与原图形完全重合,B不正确;
C图形顺时针旋转180°后,能与原图形完全重合,C不正确;
D图形顺时针旋转72°后,能与原图形完全重合,D正确;
故选:D.
分析:利用正多边形的每一个内角度数的计算方法,分别求出选项A,B,D中的多边形的一个内角的度数,由此可作出判断.
7. B
考点:图形的旋转
360°÷5=72°
故至少旋转72°后能够重合
故答案为:B
分析:用圆周角除5得到每个顶点之间的角度,即为旋转后重合的角度
8. C
考点:旋转的性质
解:∵旋转,
∴ AC=DC ,
但是旋转角不一定是 60° ,
∴ △ACD 不一定是等边三角形,
∴ AC=AD 不一定成立,即①不一定符合题意;
∵旋转,
∴ BC=EC ,故③符合题意;
∵旋转,
∴ ∠ACD=∠BCE ,
∵等腰三角形ACD和等腰三角形BCE的顶角相等,
∴它们的底角也相等,即 ∠A=∠EBC ,故④符合题意;
∵ ∠A+∠ABC=90° 不一定成立,
∴ ∠EBC+∠ABC=90° 不一定成立,
∴ AB⊥EB 不一定成立,即②不一定符合题意.
故答案为:C.
分析:根据旋转的性质,得到对应边相等,旋转角相等,从而去判断命题的正确性.
9. A
考点:旋转的性质
解:A.图形上的对应点,到旋转中心的距离相等,说法错误;
B.图形上的每一点转动的角度都相同,都等于 旋转角,说法正确;
C.当图形上的点为旋转中心时,旋转中心不动,说法正确;
D.旋转前后,两个图形全等。
故答案为:A.
分析:根据旋转的性质,分别进行判断得到答案即可。
10. B
考点:旋转的性质
解:根据旋转的性质,“69”旋转180°得到的数字为“69”
故答案为:B.
分析:根据旋转的性质,即可得到答案。
二、填空题
11. 120°
考点:旋转的性质
解:当旋转角为120°时,EF⊥BC.
理由如下:∵△DEF绕点D逆时针旋转120°,
∴∠BDE=30°,
∵∠E=60°,
∴∠E+∠BDE=90°,
∴EF⊥BC,
故答案为120°.
分析:由旋转的性质可得当旋转角为120°时,∠BDE=30°,根据∠E+∠BDE=90°,可得EF⊥BC.
12. 100
考点:旋转的性质
解:∵将等边三角形OAB绕O点按顺时针方向旋转160°,得到三角形OA'B',
∴ ∠BOB'=160° , ∠AOB=60° ,
∴ ∠1=∠BOB'-∠AOB=100° ,
故答案为:100.
分析:根据旋转的性质,可得 ∠BOB'=160° ,再根据等边三角形OAB中 ∠AOB=60° ,即可求解.
13. 90
考点:旋转的性质
解:∵△COD是由△AOB绕点O按顺时针方向旋转而得,
∴OB=OD,
∴旋转的角度是∠BOD的大小,
∵∠BOD=90°,
∴旋转的角度为90°,
故答案为: 90.
分析:由△COD是由△AOB绕点O按顺时针方向旋转而得到,再结合已知图形可知旋转的角度是∠BOD的大小,然后由图形即可求得答案
14. 30°或120°或165°
考点:图形的旋转,旋转的性质
解:如图,CD∥AB,∠BCD=∠B=30°,
∠ACD=∠ACB+∠BCD=90°+30°=120°;
如图,DE∥AB时,延长EC交AB于F,
则∠AFC=∠E=45°,
在 △ACF 中,∠ACF=180°﹣∠A﹣∠AFC,
=180°﹣60°﹣45°=75°,
∵∠DCE=90°, ?
∴∠DCF=90°, ?
∴∠ACD= ∠ACF+∠DCF=75°+90°=165° ;
如图,当 CE//AB 时,
∴∠A=∠ACE=60°, ?
∴ ?∠ACD= ∠DCE-∠ACE= 30°,
故答案为:30°或120°或165°.
分析:分CE、DE、CD与AB平行分别作出图形,再根据平行线的性质求解即可。
三、解答题
15. 解:如图所示:
考点:图形的旋转
分析:根据“面动成体”的原理,结合图形特征进行旋转,判断出旋转后的立体图形即可.
16. (1)解:如图1,OA′为所作;
(2)解:如图2,△A'B'C'为所作.
考点:旋转的性质,作图﹣旋转
分析:(1)利用网格特点和旋转的性质,画出点A的对应点A′即可;(2)利用网格特点和旋转的性质,画出点A的对应点A′、B点的对应点B′、点C的对应点C′,再顺次连接即可.
17. 解:∵△ABC绕点C顺时针方向旋转40?得△A′B′C′,
∴∠ACA′=40?,∠A=∠A′,
∵AC⊥A′B′,
∴∠A′=90°﹣40°=50°,
∴∠BAC=50°
考点:旋转的性质
分析:根据“旋转前后的图形全等”可求解。
18. (1)旋转中心为点A
(2)解:∵∠B=21°,∠ACB=26°,
∴∠BAC=180°﹣21°﹣26°=133°,
∴旋转的度数为133°
(3)解:由旋转性质知:AE=AC,AD=AB,
∴AE=AB﹣CD=2.
考点:旋转的性质
分析:(1)根据旋转的概念,得到△ABC各个顶点的对应点,再顺次连接起来,即可;
(2)根据三角形内角和定理,得到∠BAC的度数,即可求解;
(3)根据旋转的性质,得到对应边相等,进而即可求解.
19. (1)解:点D
(2)解:90°
(3)解:由旋转可得DE=DF=13,BE=AB-AE=7,BF=BC+CF=17
所以,四边形D肋F的周K=13+1 3+7+17=50
四边形DEBF的面积=正方形ABCD的面积=12×12=144
考点:旋转的性质
分析:(1)观察图形,根据旋转的性质即可确定出旋转中心;
(2)找出对应线段的夹角即为旋转角,如AD和CD之间的夹角,根据正方形的性质求解;
(3)根据旋转的性质可得AE=CF,DE=DF,根据勾股定理计算出DE的长,进而可求出四边形DEBF的周长;
根据旋转的性质可得S△ADE=S△CDF , 即可得到四边形DEBF等于正方形ABCD的面积.
