6.1.3 众数同步练习(含解析)
图片预览



文档简介
初中数学湘教版七年级下册6.1.3众数
同步练习
一、单选题(共10题;共20分)
1.数据10,10,10,11,12,12,13,13的众数是(??
)
A.?10?????????????????????????????????????????B.?11?????????????????????????????????????????C.?12?????????????????????????????????????????D.?13
2.某校为了解学生的课外阅读情况,随机抽取了一个班的学生,对他们一周的课外阅读时间进行了统计,统计数据如下表,则该班学生一周课外阅读时间的中位数和众数分别是?
(?
)
读书时间
6
小时及以下
7
小时
8
小时
9
小时
10
小时及以上
学生人数
6
11
8
8
7
A.?8,7??????????????????????????????????B.?8,8??????????????????????????????????C.?8.5,8??????????????????????????????????D.?8.5,7
3.某排球队6名场上队员的身高(单位:cm)是180,184,188,190,190,194.现用两名身高分别为185cm和188cm的队员换下场上身高为184cm和190cm的队员.与换人前相比,场上队员的身高(??
)
A.?平均数变小,众数变小???????????????????????????????????????B.?平均数变小,众数变大
C.?平均数变大,众数变小???????????????????????????????????????D.?平均数变大,众数变大
4.一组数据4,6,a,8,11的众数是11,则这组数据的中位数是(??
)
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?11
5.已知一组数据:2,5,
x
,7,9的平均数是6,则这组数据的众数是(??
).
A.?9???????????????????????????????????????????B.?7???????????????????????????????????????????C.?5???????????????????????????????????????????D.?2
6.已知数据5,3,5,4,6,5,4,下列说法正确的是(???
)
A.?中位数是4??????????????B.?众数是4??????????????C.?中位数与众数都是5??????????????D.?中位数与平均数都是5.
7.一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的平均数、中位数分别(???
)
A.?4,4????????????????????????????????????B.?3,4????????????????????????????????????C.?4,3????????????????????????????????????D.?3,3
8.两组数据:3,a
,
b
,
5与a
,
4,
2b
的平均数都是3.若将这两组数据合并为一组新数据,则这组新数据的众数为(???
)
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
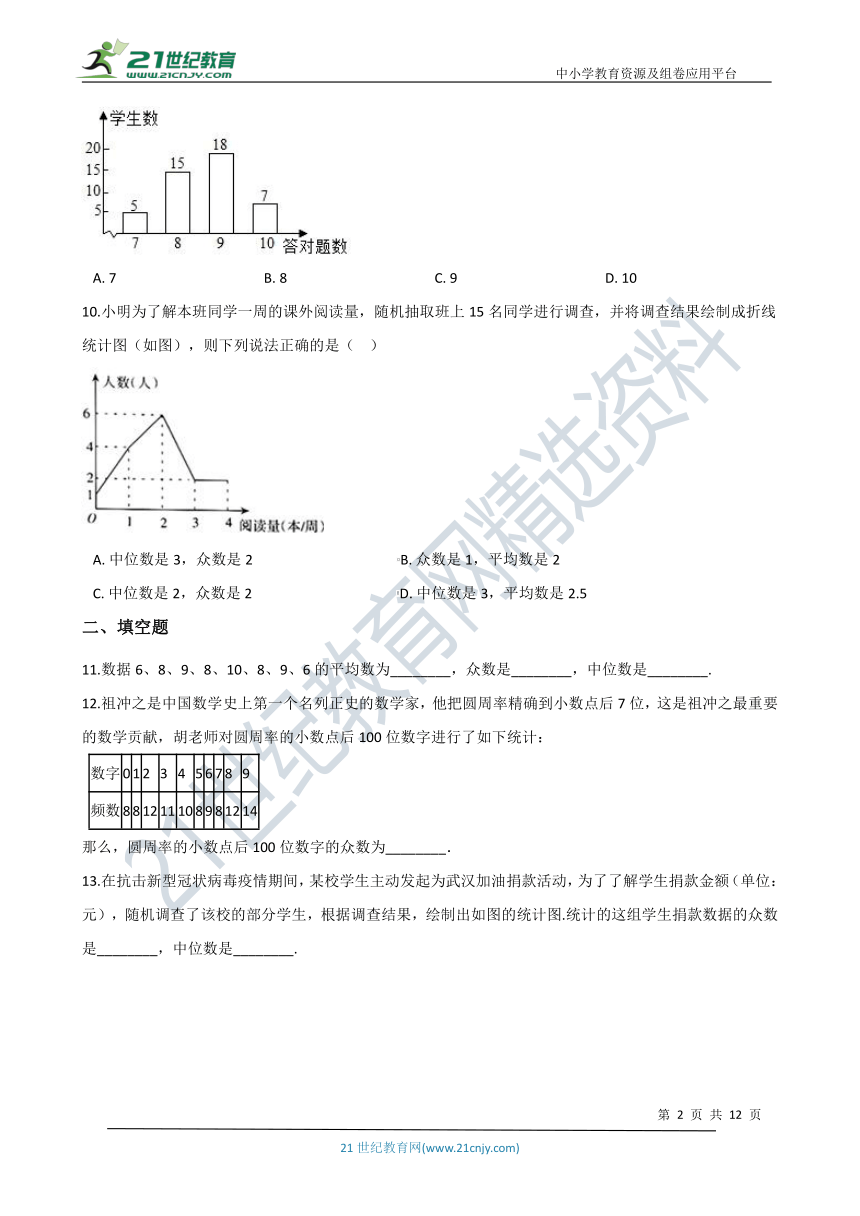
9.数学老师在课堂上给同学们布置了10个填空题作为课堂练习,并将全班同学的答题情况绘制成条形统计图.由图可知,全班同学答对题数的众数为(???
)
A.?7???????????????????????????????????????????B.?8???????????????????????????????????????????C.?9???????????????????????????????????????????D.?10
10.小明为了解本班同学一周的课外阅读量,随机抽取班上15名同学进行调查,并将调查结果绘制成折线统计图(如图),则下列说法正确的是(??
)
A.?中位数是3,众数是2??????????????????????????????????????????B.?众数是1,平均数是2
C.?中位数是2,众数是2??????????????????????????????????????????D.?中位数是3,平均数是2.5
二、填空题
11.数据6、8、9、8、10、8、9、6的平均数为________,众数是________,中位数是________.
12.祖冲之是中国数学史上第一个名列正史的数学家,他把圆周率精确到小数点后7位,这是祖冲之最重要的数学贡献,胡老师对圆周率的小数点后100位数字进行了如下统计:
数字
0
1
2
3
4
5
6
7
8
9
频数
8
8
12
11
10
8
9
8
12
14
那么,圆周率的小数点后100位数字的众数为________.
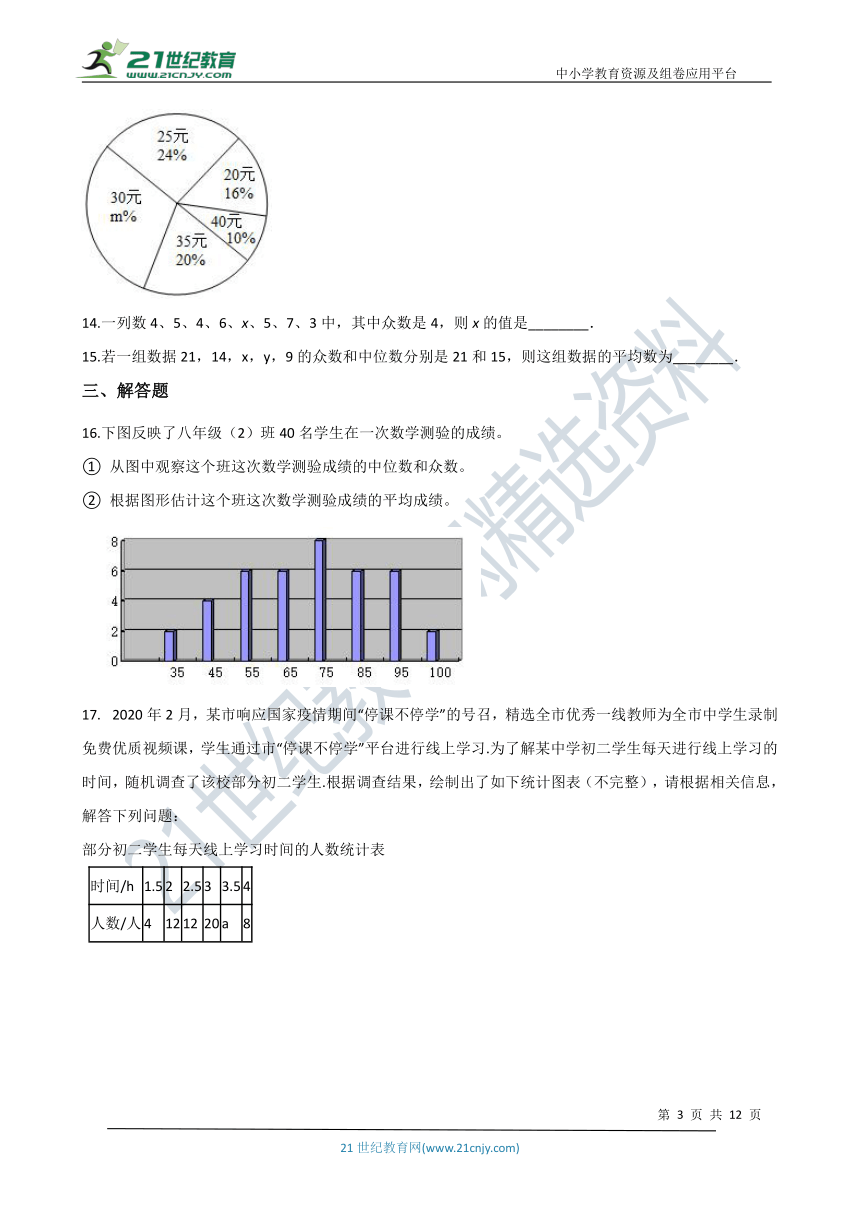
13.在抗击新型冠状病毒疫情期间,某校学生主动发起为武汉加油捐款活动,为了了解学生捐款金额(单位:元),随机调查了该校的部分学生,根据调查结果,绘制出如图的统计图.统计的这组学生捐款数据的众数是________,中位数是________.
14.一列数4、5、4、6、x、5、7、3中,其中众数是4,则x的值是________.
15.若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为________.
三、解答题
16.下图反映了八年级(2)班40名学生在一次数学测验的成绩。
①
从图中观察这个班这次数学测验成绩的中位数和众数。
②
根据图形估计这个班这次数学测验成绩的平均成绩。
17.?
2020年2月,某市响应国家疫情期间“停课不停学”的号召,精选全市优秀一线教师为全市中学生录制免费优质视频课,学生通过市“停课不停学”平台进行线上学习.为了解某中学初二学生每天进行线上学习的时间,随机调查了该校部分初二学生.根据调查结果,绘制出了如下统计图表(不完整),请根据相关信息,解答下列问题:
部分初二学生每天线上学习时间的人数统计表
时间/h
1.5
2
2.5
3
3.5
4
人数/人
4
12
12
20
a
8
(1)本次共调查的学生人数为________,在表格中,a=________;
(2)统计的这组数据中,学生每天进行线上学习时间的中位数是________,众数是________;
(3)根据样本数据,请你估计该中学初二学生每天线上学均时间是多少?
18.某学生本学期6次数学考试成绩如下表所示:
成绩类别
第一次月考
第二次月考
期中
第三次月考
第四次月考
期末
成绩/分
105
110
108
113
108
112
(1)6次考试成绩的中位数为________?,众数为________.
(2)求该生本学期四次月考的平均成绩.
(3)如果本学期的总评成绩按照月考平均成绩占20﹪、期中成绩占30﹪、期末成绩占50﹪计算,那么该生本学期的数学总评成绩是多少?
19.为了让万州区义务教育阶段学生更加深入地了解新型冠状肺炎,从而增强学生的自我防护意识,万州区教委组织了一次新型冠状肺炎相关防疫知识竞赛,通过学校选拔和推荐,对进入此次决赛的小学组和初中组各20名学生的成绩进行了整理和分析,给出了部分信息如下:
小学组学生决赛成绩统计如下:
(满分:
100
分)表1
67
89
88
65
75
76
80
85
88
92
98
100
66
73
86
86
87
95
86
78
初中组学生决赛成绩统计如下:
(满分:
100分)表
2
76
83
89
68
68
95
83
86
86
67
77
86
90
84
68
100
86
73
93
86
整理数据:(用
X
表示学生决赛成绩)表3
?
60≤x<70
70≤x<80
80≤x<90
90
分及以上
小学组学生决赛成绩
3
4
9
4
初中组学生决赛成绩
4
3
9
4
分析数据:两组样本数据的平均数、中位数、众数如表所示:表4
?
平均数
中位数
众数
优秀率(80分及以上)
小学组学生决赛成绩
83
86
b
65%
初中组学生决赛成绩
82.2
a
86
65%
(1)表中
a=
________,
b=
________?;
(2)本次决赛各组分别设一等奖
2
名,二等奖
3
名,三等奖
5
名,在初中的小虎在此次决赛中成绩为
86
分,他说只要知道一个数据就能确定是否得奖了,你认为他是根据________知道的
(填"平均数”、”中位数”、”众数”、"优秀率")
;
(3)根据表4中的数据,你认为哪个组在此次决赛中表现比较好?请说明理由.
答案解析部分
一、单选题
1.
A
考点:众数
解:数据10,10,10,11,12,12,13,13中10出现了3次,是出现次数最多的数,
∴这组数据的众数为10.
故答案为:A.
分析:根据众数是一组数据中出现次数最多的数,观察数据,可得答案.
2.
A
考点:平均数及其计算,中位数,众数
解:因为全班抽取了
6+11+8+8+7=40
人,所以一共有40个数据,且表中数据已是从小到大排列的,最中间两个数据分别为8,8,所以这一组数据的中位数是
8+82=8
,
这一组数据中出现次数最多的是7,所以众数是7.
故答案为:A.
分析:根据一组数据中出现次数最多的是众数,
中位数是指在一组数据按顺序排列后(即从大到小或从小到大),中间的那个数,若这组数据有偶数个数,中位数取中间两个数的平均数
,从而求解.
3.
A
考点:平均数及其计算,众数
解:
∵185+188=373
,
184+190=374
,
374>373
,
∴
由平均数计算公式得:与换人前相比,场上队员的身高的平均数变小,
∵
换人前的众数为190,
换人后队员的身高为180,185,188,188,190,194,其众数为188,
∴
与换人前相比,场上队员的身高的众数变小,
故答案为:A.
分析:根据平均数和众数的定义求出原数据和新数据的平均数和众数,进行比较即可得出答案.
4.
C
考点:中位数,众数
解:
∵
一组数据4,6,a,8,11的众数是11,
∴a=11,
?
把数据按从小到大重新排列为:4,6,8,11,11
所以这组数据的中位数是:8
故答案为:C.
分析:一组数据中出现次数最多的数据就是这组数据众数,据此即可得出a的值,再把数据按从小到大重新排列找出这组数据最中间位置的数即可得出这组数据的中位数.
5.
B
考点:平均数及其计算,众数
解:∵2,5,
x
,7,9的平均数是6,
∴(2+5+x+7+9)÷5=6,
∴x=7,
∴2,5,7,7,9的众数为7,
故答案为:B.
分析:先根据平均数公式求出x的值,再找出这组数中出现次数最多的数即是众数.
6.
C
考点:平均数及其计算,中位数,众数
解:把这组数据按大小顺序排列,最中间的数是5,故中位数是5;5出现的次数最多,故众数是5;平均数为
3+4×2+5×3+67=327
;由此可知A、B、D不符合题意,
故答案为:C.
分析:根据中位数、众数、平均数的含义计算数值,进行判断即可得到答案。
7.
D
考点:平均数及其计算,中位数,众数
解:∵这组数据有唯一的众数4,
∴x=4,
将数据从小到大排列为:1,2,3,3,4,4,4,
则平均数=(1+2+3+3+4+4+4)÷7=3,
中位数为:3.
故答案为:D.
分析:本题考查了众数、中位数及平均数的定义,属于基础题,掌握基本定义是关键.
8.
B
考点:平均数及其计算,众数
解:∵两组数据:3,a
,
b
,
5与a
,
4,
2b
的平均数都是3,
∴
{a+b=12-3-5a+2b=9-4
,
解得a=3,b=1,
则新数据3,3,1,5,3,4,2,
众数为3,
故答案为:B.
分析:首先根据平均数的定义列出关于a、b的二元一次方程组,再解方程组求得a、b的值,然后求众数即可.
9.
C
考点:条形统计图,众数
解:由条形统计图可得,
全班同学答对题数的众数为9,
故答案为:C
.
分析:根据统计图中的数据,可知做对9道的学生最多,从而可以得到全班同学答对题数的众数,本题得以解决.
10.
C
考点:折线统计图,平均数及其计算,中位数,众数
解:15名同学一周的课外阅读量为0,1,1,1,1,2,2,2,2,2,2,3,3,4,4,
中位数为2;
平均数为(0×1+1×4+2×6+3×2+4×2)÷15=2;
众数为2;
故答案为:C.
分析:根据统计图中的数据,求出中位数,平均数,众数,即可做出判断.
二、填空题
11.
8;8;8
考点:平均数及其计算,中位数,众数
解:平均数
=18×(6+8+9+8+10+8+9+6)=8
;
众数为:8;
中位数为:8;
故答案为:8;8;8.
分析:平均数是指一组数据中所有数据之和再除以数据的个数;中位数是先把数据从小到大(或从大到小)进行排列,如果数据的个数是奇数,那么最中间的那个数据就是中位数,如果数据的个数是偶数,那么最中间的那两个数据的平均数就是中位数;众数是一组数据中出现次数最多的数据,据此分别解答即可.
12.
9
考点:众数
解:由题目的频数分布表可观察到数字9的频数为14,出现次数最多;
故本题答案为9.
分析:众数:众数数样本观测值在频数分布表中频数最多的那一组的组中值,即在一组数据中,出现次数最多的数据,是一组数据中的原数据,而不是相应的次数.
13.
30元;30元
考点:扇形统计图,中位数,众数
解:∵m%=1﹣(24%+16%+10%+20%)=30%,
∴这组数据的众数为30元,中位数是
30+302
=30(元),
故答案为:30元,30元.
分析:首先求出30元对应的百分比,然后分别根据众数和中位数的概念求解即可.
14.
4
考点:众数
解:根据众数定义就可以得到:x=4,
故答案为:4.
分析:众数是一组数据中出现次数最多的数,根据众数的定义求出这组数的众数即可.
15.
16
考点:平均数及其计算,中位数,众数
解:∵一组数据21,14,x,y,9的众数和中位数分别是21和15,
若x=y=21,则该组数据的中位数为:21,不符合题意,
则x和y中有一个数为21,另一个数为15,
∴这组数据的平均数为:(9+14+15+21+21)÷5=16,
故答案为:16.
分析:根据已知条件分析,得出x和y中有一个数为21,再根据中位数得出另一个数,从而求出平均数.
三、解答题
16.
解:①出现最多的是75分,有8个人,故众数为75(分);
总共有40人的数学成绩,第20、21位都是75分,则中位数为75(分)
②平均数=
2×35+4×45+6×55+8×75+6×85+6×95+100×2×140=71.25
估计这个班这次数学测验成绩的平均成绩为71.25.
考点:平均数及其计算,中位数,众数
分析:①按照中位数和众数的定义解题。
②按照平均数的定义求值。
17.
(1)100;44
(2)3.5;3.5
(3)解:1.5×4%+2×12%+2.5×12%+3×20%+3.5×44%+4×8%=3.06(h),
答:该中学初二学生每天线上学均时间是3.06h.
考点:扇形统计图,中位数,众数
解:(1)4÷4%=100(人),a=100×44%=44(人),
故答案为:100,44;
(2)将这100名学生线上学习时间从小到大排列后,处在中间位置的两个数都是3.5h,因此中位数是3.5,
出现次数最多的数据是3.5h,共出现44次,因此众数是3.5,
故答案为:3.5,3.5;
分析:
(1)、根据扇形统计图各部分的百分比,计算即可.
(2)、
根据将一组数据按大小顺序排列,处在最中间位置的一个数叫做这组数据的中位数,在一组数据中出现次数最多的数叫做这组数据的众数,即可求解
.
(3)、根据随机调查该校部分初二学生的调查结果
,估计该中学初二学生每天线上学均时间,计算即可.
?
18.
(1)109;108
(2)解:平时测试的数学平均成绩=
14×(105+108+110+113)=109
(分);
(3)解:总评成绩=
109×20%+108×30%+112×50%=21.8+32.4+56=110.2
(分)
答:该生本学期的数学总评成绩为110.2分.
考点:平均数及其计算,加权平均数及其计算,中位数,众数
解:(1)这6个数从小到大排列为:105,108,108,110,112,113,中位数是
108+1102
=109,众数是108.
故答案为:109,108;
分析:(1)把6个数从小到大排列,第3与4两个数据的平均数就是这组数据的中位数,这组数据中出现次数最多的数据就是这组数据的众数;
(2)把平时测试4次的成绩相加,其和再除以4即可算出答案;
(3)取4次月考成绩平均分的20%加上期中成绩的30﹪加上期末成绩的50﹪计算即可.
19.
(1)85;86
(2)中位数
(3)解:认为小学组的同学在此次决赛中表现比较好.
因为从数据分析来看,他们在众数和优秀率相同的情况下,小学组的平均分高于初中组的平均分,说明小学组的平均水平高于初中组的平均水平;且小学组的中位数也高于初中组的中位数,说明小学组的中间水平高于初中组的中间水平;所以我认为小学组的同学在此次决赛中表现比较好.
考点:平均数及其计算,中位数,众数
解:(1)由初中组统计表可得按顺序第10、11个数是84,86;小学组86出现次数最多;
所以
a=84+862=85,
b=86.
(2)解:根据中位数的定义,可得他是根据中位数知道的;
分析:(1)根据中位数和众数的定义求解即可:由初中组统计表可得按顺序第10、11个数是84,86;小学组86出现次数最多;(2)根据中位数的定义可知,大于中位数的数占了一半;(3)可以比较众数、中位数、平均数等,有理即可
同步练习
一、单选题(共10题;共20分)
1.数据10,10,10,11,12,12,13,13的众数是(??
)
A.?10?????????????????????????????????????????B.?11?????????????????????????????????????????C.?12?????????????????????????????????????????D.?13
2.某校为了解学生的课外阅读情况,随机抽取了一个班的学生,对他们一周的课外阅读时间进行了统计,统计数据如下表,则该班学生一周课外阅读时间的中位数和众数分别是?
(?
)
读书时间
6
小时及以下
7
小时
8
小时
9
小时
10
小时及以上
学生人数
6
11
8
8
7
A.?8,7??????????????????????????????????B.?8,8??????????????????????????????????C.?8.5,8??????????????????????????????????D.?8.5,7
3.某排球队6名场上队员的身高(单位:cm)是180,184,188,190,190,194.现用两名身高分别为185cm和188cm的队员换下场上身高为184cm和190cm的队员.与换人前相比,场上队员的身高(??
)
A.?平均数变小,众数变小???????????????????????????????????????B.?平均数变小,众数变大
C.?平均数变大,众数变小???????????????????????????????????????D.?平均数变大,众数变大
4.一组数据4,6,a,8,11的众数是11,则这组数据的中位数是(??
)
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?11
5.已知一组数据:2,5,
x
,7,9的平均数是6,则这组数据的众数是(??
).
A.?9???????????????????????????????????????????B.?7???????????????????????????????????????????C.?5???????????????????????????????????????????D.?2
6.已知数据5,3,5,4,6,5,4,下列说法正确的是(???
)
A.?中位数是4??????????????B.?众数是4??????????????C.?中位数与众数都是5??????????????D.?中位数与平均数都是5.
7.一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的平均数、中位数分别(???
)
A.?4,4????????????????????????????????????B.?3,4????????????????????????????????????C.?4,3????????????????????????????????????D.?3,3
8.两组数据:3,a
,
b
,
5与a
,
4,
2b
的平均数都是3.若将这两组数据合并为一组新数据,则这组新数据的众数为(???
)
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
9.数学老师在课堂上给同学们布置了10个填空题作为课堂练习,并将全班同学的答题情况绘制成条形统计图.由图可知,全班同学答对题数的众数为(???
)
A.?7???????????????????????????????????????????B.?8???????????????????????????????????????????C.?9???????????????????????????????????????????D.?10
10.小明为了解本班同学一周的课外阅读量,随机抽取班上15名同学进行调查,并将调查结果绘制成折线统计图(如图),则下列说法正确的是(??
)
A.?中位数是3,众数是2??????????????????????????????????????????B.?众数是1,平均数是2
C.?中位数是2,众数是2??????????????????????????????????????????D.?中位数是3,平均数是2.5
二、填空题
11.数据6、8、9、8、10、8、9、6的平均数为________,众数是________,中位数是________.
12.祖冲之是中国数学史上第一个名列正史的数学家,他把圆周率精确到小数点后7位,这是祖冲之最重要的数学贡献,胡老师对圆周率的小数点后100位数字进行了如下统计:
数字
0
1
2
3
4
5
6
7
8
9
频数
8
8
12
11
10
8
9
8
12
14
那么,圆周率的小数点后100位数字的众数为________.
13.在抗击新型冠状病毒疫情期间,某校学生主动发起为武汉加油捐款活动,为了了解学生捐款金额(单位:元),随机调查了该校的部分学生,根据调查结果,绘制出如图的统计图.统计的这组学生捐款数据的众数是________,中位数是________.
14.一列数4、5、4、6、x、5、7、3中,其中众数是4,则x的值是________.
15.若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为________.
三、解答题
16.下图反映了八年级(2)班40名学生在一次数学测验的成绩。
①
从图中观察这个班这次数学测验成绩的中位数和众数。
②
根据图形估计这个班这次数学测验成绩的平均成绩。
17.?
2020年2月,某市响应国家疫情期间“停课不停学”的号召,精选全市优秀一线教师为全市中学生录制免费优质视频课,学生通过市“停课不停学”平台进行线上学习.为了解某中学初二学生每天进行线上学习的时间,随机调查了该校部分初二学生.根据调查结果,绘制出了如下统计图表(不完整),请根据相关信息,解答下列问题:
部分初二学生每天线上学习时间的人数统计表
时间/h
1.5
2
2.5
3
3.5
4
人数/人
4
12
12
20
a
8
(1)本次共调查的学生人数为________,在表格中,a=________;
(2)统计的这组数据中,学生每天进行线上学习时间的中位数是________,众数是________;
(3)根据样本数据,请你估计该中学初二学生每天线上学均时间是多少?
18.某学生本学期6次数学考试成绩如下表所示:
成绩类别
第一次月考
第二次月考
期中
第三次月考
第四次月考
期末
成绩/分
105
110
108
113
108
112
(1)6次考试成绩的中位数为________?,众数为________.
(2)求该生本学期四次月考的平均成绩.
(3)如果本学期的总评成绩按照月考平均成绩占20﹪、期中成绩占30﹪、期末成绩占50﹪计算,那么该生本学期的数学总评成绩是多少?
19.为了让万州区义务教育阶段学生更加深入地了解新型冠状肺炎,从而增强学生的自我防护意识,万州区教委组织了一次新型冠状肺炎相关防疫知识竞赛,通过学校选拔和推荐,对进入此次决赛的小学组和初中组各20名学生的成绩进行了整理和分析,给出了部分信息如下:
小学组学生决赛成绩统计如下:
(满分:
100
分)表1
67
89
88
65
75
76
80
85
88
92
98
100
66
73
86
86
87
95
86
78
初中组学生决赛成绩统计如下:
(满分:
100分)表
2
76
83
89
68
68
95
83
86
86
67
77
86
90
84
68
100
86
73
93
86
整理数据:(用
X
表示学生决赛成绩)表3
?
60≤x<70
70≤x<80
80≤x<90
90
分及以上
小学组学生决赛成绩
3
4
9
4
初中组学生决赛成绩
4
3
9
4
分析数据:两组样本数据的平均数、中位数、众数如表所示:表4
?
平均数
中位数
众数
优秀率(80分及以上)
小学组学生决赛成绩
83
86
b
65%
初中组学生决赛成绩
82.2
a
86
65%
(1)表中
a=
________,
b=
________?;
(2)本次决赛各组分别设一等奖
2
名,二等奖
3
名,三等奖
5
名,在初中的小虎在此次决赛中成绩为
86
分,他说只要知道一个数据就能确定是否得奖了,你认为他是根据________知道的
(填"平均数”、”中位数”、”众数”、"优秀率")
;
(3)根据表4中的数据,你认为哪个组在此次决赛中表现比较好?请说明理由.
答案解析部分
一、单选题
1.
A
考点:众数
解:数据10,10,10,11,12,12,13,13中10出现了3次,是出现次数最多的数,
∴这组数据的众数为10.
故答案为:A.
分析:根据众数是一组数据中出现次数最多的数,观察数据,可得答案.
2.
A
考点:平均数及其计算,中位数,众数
解:因为全班抽取了
6+11+8+8+7=40
人,所以一共有40个数据,且表中数据已是从小到大排列的,最中间两个数据分别为8,8,所以这一组数据的中位数是
8+82=8
,
这一组数据中出现次数最多的是7,所以众数是7.
故答案为:A.
分析:根据一组数据中出现次数最多的是众数,
中位数是指在一组数据按顺序排列后(即从大到小或从小到大),中间的那个数,若这组数据有偶数个数,中位数取中间两个数的平均数
,从而求解.
3.
A
考点:平均数及其计算,众数
解:
∵185+188=373
,
184+190=374
,
374>373
,
∴
由平均数计算公式得:与换人前相比,场上队员的身高的平均数变小,
∵
换人前的众数为190,
换人后队员的身高为180,185,188,188,190,194,其众数为188,
∴
与换人前相比,场上队员的身高的众数变小,
故答案为:A.
分析:根据平均数和众数的定义求出原数据和新数据的平均数和众数,进行比较即可得出答案.
4.
C
考点:中位数,众数
解:
∵
一组数据4,6,a,8,11的众数是11,
∴a=11,
?
把数据按从小到大重新排列为:4,6,8,11,11
所以这组数据的中位数是:8
故答案为:C.
分析:一组数据中出现次数最多的数据就是这组数据众数,据此即可得出a的值,再把数据按从小到大重新排列找出这组数据最中间位置的数即可得出这组数据的中位数.
5.
B
考点:平均数及其计算,众数
解:∵2,5,
x
,7,9的平均数是6,
∴(2+5+x+7+9)÷5=6,
∴x=7,
∴2,5,7,7,9的众数为7,
故答案为:B.
分析:先根据平均数公式求出x的值,再找出这组数中出现次数最多的数即是众数.
6.
C
考点:平均数及其计算,中位数,众数
解:把这组数据按大小顺序排列,最中间的数是5,故中位数是5;5出现的次数最多,故众数是5;平均数为
3+4×2+5×3+67=327
;由此可知A、B、D不符合题意,
故答案为:C.
分析:根据中位数、众数、平均数的含义计算数值,进行判断即可得到答案。
7.
D
考点:平均数及其计算,中位数,众数
解:∵这组数据有唯一的众数4,
∴x=4,
将数据从小到大排列为:1,2,3,3,4,4,4,
则平均数=(1+2+3+3+4+4+4)÷7=3,
中位数为:3.
故答案为:D.
分析:本题考查了众数、中位数及平均数的定义,属于基础题,掌握基本定义是关键.
8.
B
考点:平均数及其计算,众数
解:∵两组数据:3,a
,
b
,
5与a
,
4,
2b
的平均数都是3,
∴
{a+b=12-3-5a+2b=9-4
,
解得a=3,b=1,
则新数据3,3,1,5,3,4,2,
众数为3,
故答案为:B.
分析:首先根据平均数的定义列出关于a、b的二元一次方程组,再解方程组求得a、b的值,然后求众数即可.
9.
C
考点:条形统计图,众数
解:由条形统计图可得,
全班同学答对题数的众数为9,
故答案为:C
.
分析:根据统计图中的数据,可知做对9道的学生最多,从而可以得到全班同学答对题数的众数,本题得以解决.
10.
C
考点:折线统计图,平均数及其计算,中位数,众数
解:15名同学一周的课外阅读量为0,1,1,1,1,2,2,2,2,2,2,3,3,4,4,
中位数为2;
平均数为(0×1+1×4+2×6+3×2+4×2)÷15=2;
众数为2;
故答案为:C.
分析:根据统计图中的数据,求出中位数,平均数,众数,即可做出判断.
二、填空题
11.
8;8;8
考点:平均数及其计算,中位数,众数
解:平均数
=18×(6+8+9+8+10+8+9+6)=8
;
众数为:8;
中位数为:8;
故答案为:8;8;8.
分析:平均数是指一组数据中所有数据之和再除以数据的个数;中位数是先把数据从小到大(或从大到小)进行排列,如果数据的个数是奇数,那么最中间的那个数据就是中位数,如果数据的个数是偶数,那么最中间的那两个数据的平均数就是中位数;众数是一组数据中出现次数最多的数据,据此分别解答即可.
12.
9
考点:众数
解:由题目的频数分布表可观察到数字9的频数为14,出现次数最多;
故本题答案为9.
分析:众数:众数数样本观测值在频数分布表中频数最多的那一组的组中值,即在一组数据中,出现次数最多的数据,是一组数据中的原数据,而不是相应的次数.
13.
30元;30元
考点:扇形统计图,中位数,众数
解:∵m%=1﹣(24%+16%+10%+20%)=30%,
∴这组数据的众数为30元,中位数是
30+302
=30(元),
故答案为:30元,30元.
分析:首先求出30元对应的百分比,然后分别根据众数和中位数的概念求解即可.
14.
4
考点:众数
解:根据众数定义就可以得到:x=4,
故答案为:4.
分析:众数是一组数据中出现次数最多的数,根据众数的定义求出这组数的众数即可.
15.
16
考点:平均数及其计算,中位数,众数
解:∵一组数据21,14,x,y,9的众数和中位数分别是21和15,
若x=y=21,则该组数据的中位数为:21,不符合题意,
则x和y中有一个数为21,另一个数为15,
∴这组数据的平均数为:(9+14+15+21+21)÷5=16,
故答案为:16.
分析:根据已知条件分析,得出x和y中有一个数为21,再根据中位数得出另一个数,从而求出平均数.
三、解答题
16.
解:①出现最多的是75分,有8个人,故众数为75(分);
总共有40人的数学成绩,第20、21位都是75分,则中位数为75(分)
②平均数=
2×35+4×45+6×55+8×75+6×85+6×95+100×2×140=71.25
估计这个班这次数学测验成绩的平均成绩为71.25.
考点:平均数及其计算,中位数,众数
分析:①按照中位数和众数的定义解题。
②按照平均数的定义求值。
17.
(1)100;44
(2)3.5;3.5
(3)解:1.5×4%+2×12%+2.5×12%+3×20%+3.5×44%+4×8%=3.06(h),
答:该中学初二学生每天线上学均时间是3.06h.
考点:扇形统计图,中位数,众数
解:(1)4÷4%=100(人),a=100×44%=44(人),
故答案为:100,44;
(2)将这100名学生线上学习时间从小到大排列后,处在中间位置的两个数都是3.5h,因此中位数是3.5,
出现次数最多的数据是3.5h,共出现44次,因此众数是3.5,
故答案为:3.5,3.5;
分析:
(1)、根据扇形统计图各部分的百分比,计算即可.
(2)、
根据将一组数据按大小顺序排列,处在最中间位置的一个数叫做这组数据的中位数,在一组数据中出现次数最多的数叫做这组数据的众数,即可求解
.
(3)、根据随机调查该校部分初二学生的调查结果
,估计该中学初二学生每天线上学均时间,计算即可.
?
18.
(1)109;108
(2)解:平时测试的数学平均成绩=
14×(105+108+110+113)=109
(分);
(3)解:总评成绩=
109×20%+108×30%+112×50%=21.8+32.4+56=110.2
(分)
答:该生本学期的数学总评成绩为110.2分.
考点:平均数及其计算,加权平均数及其计算,中位数,众数
解:(1)这6个数从小到大排列为:105,108,108,110,112,113,中位数是
108+1102
=109,众数是108.
故答案为:109,108;
分析:(1)把6个数从小到大排列,第3与4两个数据的平均数就是这组数据的中位数,这组数据中出现次数最多的数据就是这组数据的众数;
(2)把平时测试4次的成绩相加,其和再除以4即可算出答案;
(3)取4次月考成绩平均分的20%加上期中成绩的30﹪加上期末成绩的50﹪计算即可.
19.
(1)85;86
(2)中位数
(3)解:认为小学组的同学在此次决赛中表现比较好.
因为从数据分析来看,他们在众数和优秀率相同的情况下,小学组的平均分高于初中组的平均分,说明小学组的平均水平高于初中组的平均水平;且小学组的中位数也高于初中组的中位数,说明小学组的中间水平高于初中组的中间水平;所以我认为小学组的同学在此次决赛中表现比较好.
考点:平均数及其计算,中位数,众数
解:(1)由初中组统计表可得按顺序第10、11个数是84,86;小学组86出现次数最多;
所以
a=84+862=85,
b=86.
(2)解:根据中位数的定义,可得他是根据中位数知道的;
分析:(1)根据中位数和众数的定义求解即可:由初中组统计表可得按顺序第10、11个数是84,86;小学组86出现次数最多;(2)根据中位数的定义可知,大于中位数的数占了一半;(3)可以比较众数、中位数、平均数等,有理即可
