5.3 图形变换的简单应用同步练习(含解析 )
文档属性
| 名称 | 5.3 图形变换的简单应用同步练习(含解析 ) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 17:53:53 | ||
图片预览


文档简介
初中数学湘教版七年级下册5.3图形变换的简单应用 同步练习
一、单选题
1.下列图案中,含有旋转变换的有(???? ) .
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
2.如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标,其中可以看着是由“基本图案”经过平移得到的是(?? )
A.?奥迪??????B.?本田??????C.?大众??????D.?铃木
3.下列各项中,不是由平移设计的是(?? )
A.???????????????????????????B.?? ?????????????????????????C.??????????????????????????D.?
4.下列基本图形中,经过平移、旋转或轴对称变换后,不能得到如图的是( )
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
5.下列图案中,可以由一个”基本图案”连续旋转45°得到的是( ?????)
A.?????????????????B.?????????????????C.?????????????????D.?
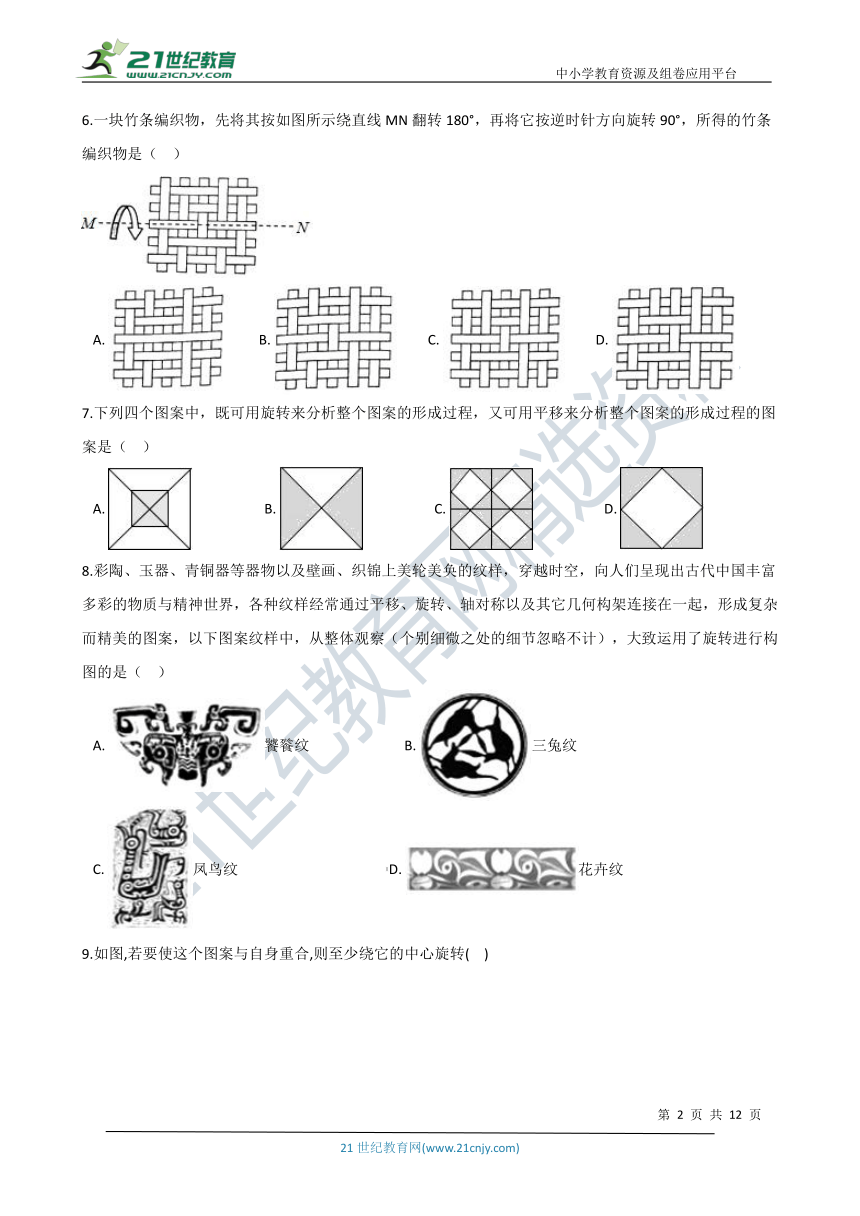
6.一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是(?? )
A.?????????B.?????????C.?????????D.?
7.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是(?? )
A.??????????????????????B.??????????????????????C.??????????????????????D.?
8.彩陶、玉器、青铜器等器物以及壁画、织锦上美轮美奂的纹样,穿越时空,向人们呈现出古代中国丰富多彩的物质与精神世界,各种纹样经常通过平移、旋转、轴对称以及其它几何构架连接在一起,形成复杂而精美的图案,以下图案纹样中,从整体观察(个别细微之处的细节忽略不计),大致运用了旋转进行构图的是(?? )
A.?饕餮纹???????????????????????????B.?三兔纹
C.?凤鸟纹???????????????????????????????????????????D.?花卉纹
9.如图,若要使这个图案与自身重合,则至少绕它的中心旋转(?? )
A.?45°?????????????????????????????????????B.?90°?????????????????????????????????????C.?135°?????????????????????????????????????D.?180°
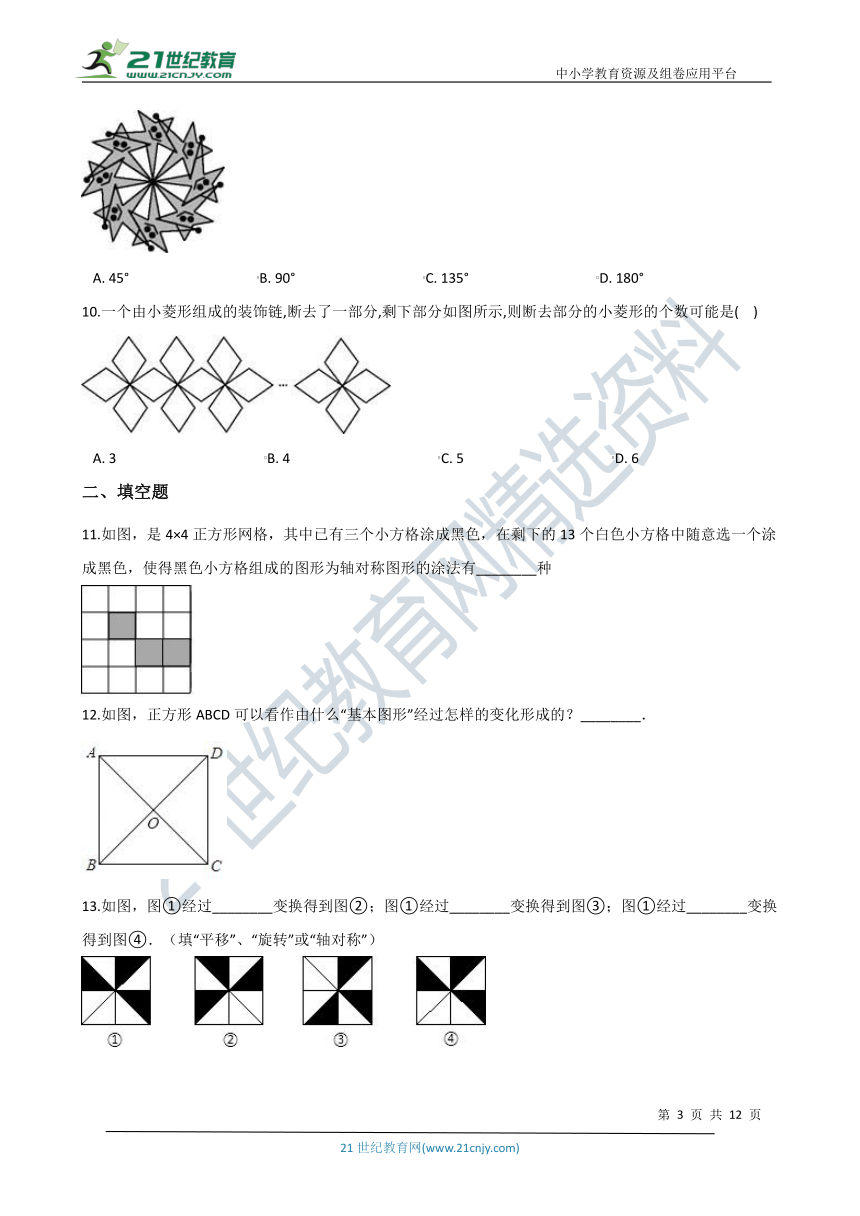
10.一个由小菱形组成的装饰链,断去了一部分,剩下部分如图所示,则断去部分的小菱形的个数可能是(?? )
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
二、填空题
11.如图,是4×4正方形网格,其中已有三个小方格涂成黑色,在剩下的13个白色小方格中随意选一个涂成黑色,使得黑色小方格组成的图形为轴对称图形的涂法有________种
12.如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的?________.
13.如图,图①经过________变换得到图②;图①经过________变换得到图③;图①经过________变换得到图④.(填“平移”、“旋转”或“轴对称”)
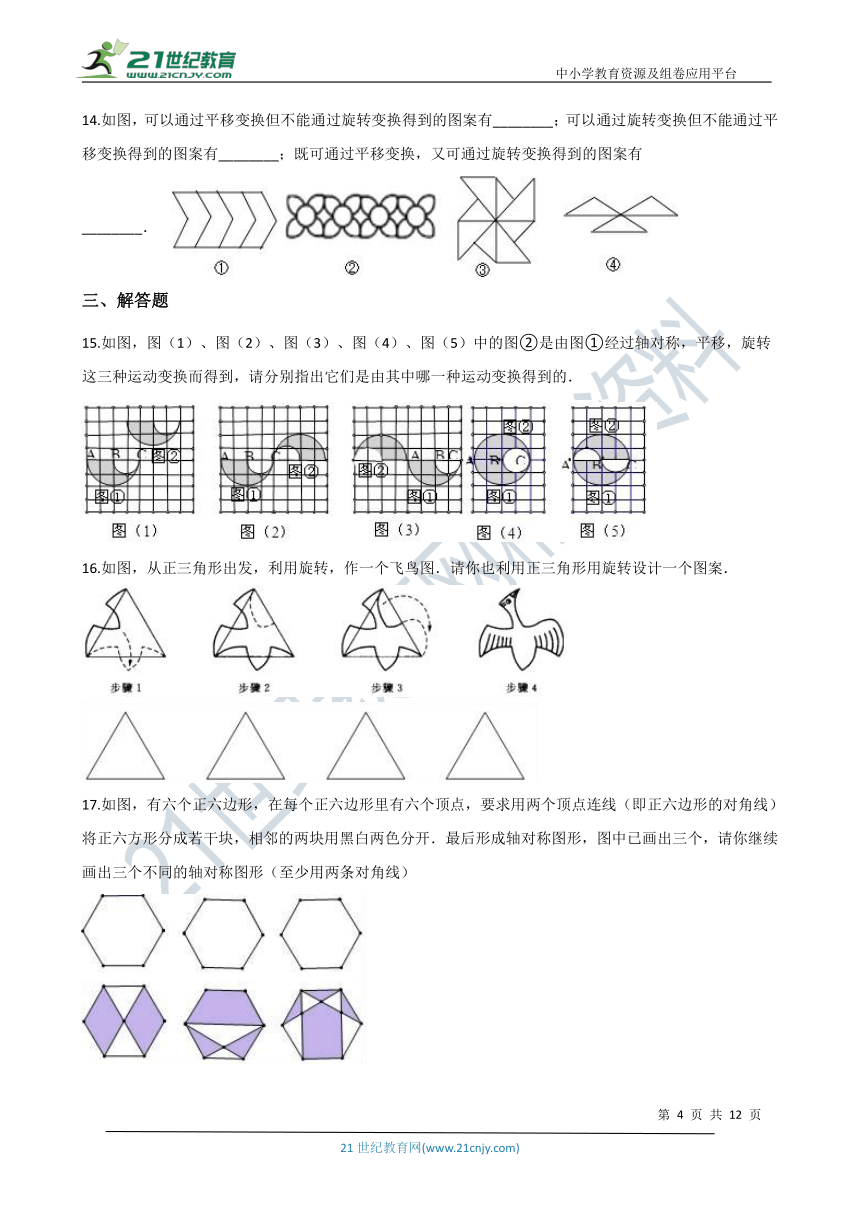
14.如图,可以通过平移变换但不能通过旋转变换得到的图案有________;可以通过旋转变换但不能通过平移变换得到的图案有________;既可通过平移变换,又可通过旋转变换得到的图案有________.
三、解答题
15.如图,图(1)、图(2)、图(3)、图(4)、图(5)中的图②是由图①经过轴对称,平移,旋转这三种运动变换而得到,请分别指出它们是由其中哪一种运动变换得到的.
16.如图,从正三角形出发,利用旋转,作一个飞鸟图.请你也利用正三角形用旋转设计一个图案.
17.如图,有六个正六边形,在每个正六边形里有六个顶点,要求用两个顶点连线(即正六边形的对角线)将正六方形分成若干块,相邻的两块用黑白两色分开.最后形成轴对称图形,图中已画出三个,请你继续画出三个不同的轴对称图形(至少用两条对角线)
18.如图1为 L 形的一种三格骨牌,它是由三个全等的正方形连接而成.请以 L 形的三格骨牌为基本图形,在图2,图3中各设计一个轴对称图形,要求如下:
(1)每个图形由两个 L 形三格骨牌组成,骨牌的顶点都在小正方形的顶点上.?
(2)设计的图形用斜线涂出,若形状相同,则视为一种.
19.认真观察图(1)﹣(4)中的四个图案,回答下列问题:
(1)请写出这四个图案都具有的两个共同特征:特征1:________;特征2:________.
(2)请你在图5中设计出你心中最美的图案,使它也具备你所写出的上述特征.
答案解析部分
一、单选题
1. A
考点:利用旋转设计图案
解:根据旋转的含义可知:选项中给出的4个图都可以通过旋转得到,
其中第2个图形也可以通过轴对称得到,第3个也可以利用平移得到,
故答案为:A.
分析:根据利用旋转设计图案关键是利用旋转中的三个要素(①旋转中心; ②旋转方向; ③旋转角度)设计图案.通过旋转变换不同角度或者绕着不同的旋转中心向着不同的方向进行旋转都可设计出美丽的图案,进而判断得出即可.
2. A
考点:利用平移设计图案
解:观察图形可知,图案A可以看作由“基本图案”经过平移得到.
故答案为:A.
分析:根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得出符合题意的答案.
3. D
考点:利用平移设计图案,旋转对称图形
解:D项是由旋转得到的,不是平移
故答案为:D
分析:根据旋转和平移的性质可求解。
4. C
考点:作图﹣轴对称,利用平移设计图案,利用旋转设计图案
解:A.经过平移可得到上图,错误;B.经过旋转可得到上图,错误;C.经过平移、旋转或轴对称变换后,都不能得到上图,正确;D.经过旋转可得到上图,错误.
故答案为:C.
分析:根据平移、旋转或轴对称的定义作出判断即可.
5. B
考点:利用旋转设计图案
解:A、由基本图形连续旋转90°得到,因此此选项不符合题意;
B、由基本图形连续旋转45°得到,因此此选项符合题意;
C、由基本图形连续旋转60°得到,因此此选项不符合题意;
D、由基本图形连续旋转90°得到,因此此选项不符合题意;
故答案为:B
分析:要由一个”基本图案”连续旋转45°得到的,可知整个图案应有8个基本图案组成的,观察四个选项中的图案,即可得出答案。
6. B
考点:利用旋转设计图案
解:先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是B,
故选B.
分析:根据轴对称和旋转的性质即可得到结论.
7. C
考点:利用平移设计图案,利用旋转设计图案
解:
A、B、C、D四个选项中的图形都可以看成是图形的一半旋转180°得到,
若一个图形可以通过某一个基本图形平移得到,则这个图形可以分成几个相同的基本图形,且基本图形之间对应点的连线应该是平行的,
故A、B、D不能由平移得到,只有C选项的图形,可看成是由基本图形 通过平移得到,
故选C.
分析:分别根据旋转的定义及平移的定义逐项分析即可.
8. B
考点:利用轴对称设计图案,利用平移设计图案,利用旋转设计图案
解:A、图中利用的是对称,错误;
B、图中利用的是旋转,正确;
C、图中利用的位似,错误;
D、图中利用的是平移,错误;
故选B
分析:根据旋转的性质与特点判断即可.
9. A
考点:旋转的性质,利用旋转设计图案
解:整个图案可以看成是一个正八边形的旋转,至少旋转360°8=45°。
故答案为:A
分析:根据旋转的性质,旋转的角度不变,而整个图案是一个正八边形,即可求出旋转角的度数。
10. C
考点:生活中的平移现象,利用平移设计图案
解:如图,可知断去的小菱形的个数为5个。
分析:根据题意可知断去的菱形个数均为较小的正整数,由所示的图形规律画出完整的装饰链,可得断去部分的小菱形的个数。
二、填空题
11. 2.
考点:利用轴对称设计图案
解:如图所示:
在剩下的13个白色小方格中随意选一个涂成黑色,使得黑色小方格组成的图形为轴对称图形的涂法有2种,
故答案为:2.
分析:把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形,根据定义即可判断出可以涂色的图形.
12. 把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD
考点:利用旋转设计图案
解:观察图形可知把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD.
故答案为:把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD
分析:旋转的性质:①旋转后的每一点都绕着旋转中心,旋转了同样大小的角度;②旋转后的图形与原来图形的形状与大小都没有发生变化,③旋转前后两个图形的对应点到旋转中心的距离相等;④对应点到旋转中心的连线所成的角相等.观察图形,回想正方形的特性; 根据旋转变换图形的性质即可得出答案.
13. 轴对称;旋转;平移
考点:利用轴对称设计图案,利用平移设计图案,利用旋转设计图案
解:图①经过轴对称变换得到图②;图①经过旋转变换得到图③;图①经过平移变换得到图④.
故答案为:轴对称;旋转;平移.
分析:根据轴对称、旋转和平移的定义,直接求解.
14.①④;③;②
考点:利用平移设计图案,利用旋转设计图案
解:可以通过平移变换但不能通过旋转变换得到的图案有①④; 可以通过旋转变换但不能通过平移变换得到的图案有③;既可通过平移变换,又可通过旋转变换得到的图案有②.
故答案为:①④,③,②.
分析:分别根据平移的性质以及旋转的性质进而判断得出即可.
三、解答题
15. 解:图(1)中的图②是由图①经过平移变换而得到;
图(2)中的图②是由图①经过旋转变换而得到(绕点C旋转180°);
图(3)中的图②是由图①经过旋转变换而得到(绕点A旋转180°);
图(4)中的图②是由图①经过轴对称变换而得到(以AC所在的直线为对称轴);
图(5)中的图②是由图①经过旋转变换而得到(绕点B旋转180°)
考点:利用轴对称设计图案,利用平移设计图案,利用旋转设计图案
分析:图(1)中两个图形的方向没有改变,那么是平移得到的,看对应点C的平移即可;图(2)中两个图形的方向改变,那么是旋转得到的,C点位置没有变,是旋转中心,AB和它的对应边在一条直线上,那么旋转角度是180°;
图(3)中两个图形的方向改变,那么是旋转得到的,A点位置没有变,是旋转中心,AB和它的对应边在一条直线上,那么旋转角度是180°;图(4)中各对应点重合,那么是翻折得到的,对应点所在的直线即为对称轴;图(5)中,B点位置没有变,是旋转中心,AB和它的对应边在一条直线上,那么旋转角度是180°.
16.解:先以等边三角形的一边为基础画一个基本图形,再绕等边三角形的两个顶点分别旋转60°后删除原等边三角形.
如图所示:
考点:利用旋转设计图案
分析:利用旋转设计图案,此题答案不唯一,先以等边三角形的一边为基础画一个基本图形,再绕等边三角形的两个顶点分别旋转60°后删除原等边三角形.
17. 解:如图所示.
考点:利用轴对称设计图案
分析:根据轴对称的定义和六边形的性质求解可得.
18. (1)解:如图,即为所求作的轴对称图形。
(2)解:如图,即为所求作的轴对称图形.
考点:利用轴对称设计图案
分析:根据轴对称的图形的定义及题中要求设计即可.
19. (1)都是轴对称图形;都是中心对称图形
(2)解:如图所示,
考点:轴对称图形,利用轴对称设计图案,中心对称及中心对称图形,利用旋转设计图案
解:试题解析:(1)特征1:都是轴对称图形;
特征2:都是中心对称图形,
故答案为:都是轴对称图形;都是中心对称图形;
分析:(1)中心对称图形:把一个图形绕着某一点旋转180°后,如果旋转后的图形能够与原来的图形重合,轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;据此解答即可.
(2)根据(1)中的特征画出图形即可(答案不唯一).
一、单选题
1.下列图案中,含有旋转变换的有(???? ) .
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
2.如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标,其中可以看着是由“基本图案”经过平移得到的是(?? )
A.?奥迪??????B.?本田??????C.?大众??????D.?铃木
3.下列各项中,不是由平移设计的是(?? )
A.???????????????????????????B.?? ?????????????????????????C.??????????????????????????D.?
4.下列基本图形中,经过平移、旋转或轴对称变换后,不能得到如图的是( )
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
5.下列图案中,可以由一个”基本图案”连续旋转45°得到的是( ?????)
A.?????????????????B.?????????????????C.?????????????????D.?
6.一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是(?? )
A.?????????B.?????????C.?????????D.?
7.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是(?? )
A.??????????????????????B.??????????????????????C.??????????????????????D.?
8.彩陶、玉器、青铜器等器物以及壁画、织锦上美轮美奂的纹样,穿越时空,向人们呈现出古代中国丰富多彩的物质与精神世界,各种纹样经常通过平移、旋转、轴对称以及其它几何构架连接在一起,形成复杂而精美的图案,以下图案纹样中,从整体观察(个别细微之处的细节忽略不计),大致运用了旋转进行构图的是(?? )
A.?饕餮纹???????????????????????????B.?三兔纹
C.?凤鸟纹???????????????????????????????????????????D.?花卉纹
9.如图,若要使这个图案与自身重合,则至少绕它的中心旋转(?? )
A.?45°?????????????????????????????????????B.?90°?????????????????????????????????????C.?135°?????????????????????????????????????D.?180°
10.一个由小菱形组成的装饰链,断去了一部分,剩下部分如图所示,则断去部分的小菱形的个数可能是(?? )
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
二、填空题
11.如图,是4×4正方形网格,其中已有三个小方格涂成黑色,在剩下的13个白色小方格中随意选一个涂成黑色,使得黑色小方格组成的图形为轴对称图形的涂法有________种
12.如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的?________.
13.如图,图①经过________变换得到图②;图①经过________变换得到图③;图①经过________变换得到图④.(填“平移”、“旋转”或“轴对称”)
14.如图,可以通过平移变换但不能通过旋转变换得到的图案有________;可以通过旋转变换但不能通过平移变换得到的图案有________;既可通过平移变换,又可通过旋转变换得到的图案有________.
三、解答题
15.如图,图(1)、图(2)、图(3)、图(4)、图(5)中的图②是由图①经过轴对称,平移,旋转这三种运动变换而得到,请分别指出它们是由其中哪一种运动变换得到的.
16.如图,从正三角形出发,利用旋转,作一个飞鸟图.请你也利用正三角形用旋转设计一个图案.
17.如图,有六个正六边形,在每个正六边形里有六个顶点,要求用两个顶点连线(即正六边形的对角线)将正六方形分成若干块,相邻的两块用黑白两色分开.最后形成轴对称图形,图中已画出三个,请你继续画出三个不同的轴对称图形(至少用两条对角线)
18.如图1为 L 形的一种三格骨牌,它是由三个全等的正方形连接而成.请以 L 形的三格骨牌为基本图形,在图2,图3中各设计一个轴对称图形,要求如下:
(1)每个图形由两个 L 形三格骨牌组成,骨牌的顶点都在小正方形的顶点上.?
(2)设计的图形用斜线涂出,若形状相同,则视为一种.
19.认真观察图(1)﹣(4)中的四个图案,回答下列问题:
(1)请写出这四个图案都具有的两个共同特征:特征1:________;特征2:________.
(2)请你在图5中设计出你心中最美的图案,使它也具备你所写出的上述特征.
答案解析部分
一、单选题
1. A
考点:利用旋转设计图案
解:根据旋转的含义可知:选项中给出的4个图都可以通过旋转得到,
其中第2个图形也可以通过轴对称得到,第3个也可以利用平移得到,
故答案为:A.
分析:根据利用旋转设计图案关键是利用旋转中的三个要素(①旋转中心; ②旋转方向; ③旋转角度)设计图案.通过旋转变换不同角度或者绕着不同的旋转中心向着不同的方向进行旋转都可设计出美丽的图案,进而判断得出即可.
2. A
考点:利用平移设计图案
解:观察图形可知,图案A可以看作由“基本图案”经过平移得到.
故答案为:A.
分析:根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得出符合题意的答案.
3. D
考点:利用平移设计图案,旋转对称图形
解:D项是由旋转得到的,不是平移
故答案为:D
分析:根据旋转和平移的性质可求解。
4. C
考点:作图﹣轴对称,利用平移设计图案,利用旋转设计图案
解:A.经过平移可得到上图,错误;B.经过旋转可得到上图,错误;C.经过平移、旋转或轴对称变换后,都不能得到上图,正确;D.经过旋转可得到上图,错误.
故答案为:C.
分析:根据平移、旋转或轴对称的定义作出判断即可.
5. B
考点:利用旋转设计图案
解:A、由基本图形连续旋转90°得到,因此此选项不符合题意;
B、由基本图形连续旋转45°得到,因此此选项符合题意;
C、由基本图形连续旋转60°得到,因此此选项不符合题意;
D、由基本图形连续旋转90°得到,因此此选项不符合题意;
故答案为:B
分析:要由一个”基本图案”连续旋转45°得到的,可知整个图案应有8个基本图案组成的,观察四个选项中的图案,即可得出答案。
6. B
考点:利用旋转设计图案
解:先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是B,
故选B.
分析:根据轴对称和旋转的性质即可得到结论.
7. C
考点:利用平移设计图案,利用旋转设计图案
解:
A、B、C、D四个选项中的图形都可以看成是图形的一半旋转180°得到,
若一个图形可以通过某一个基本图形平移得到,则这个图形可以分成几个相同的基本图形,且基本图形之间对应点的连线应该是平行的,
故A、B、D不能由平移得到,只有C选项的图形,可看成是由基本图形 通过平移得到,
故选C.
分析:分别根据旋转的定义及平移的定义逐项分析即可.
8. B
考点:利用轴对称设计图案,利用平移设计图案,利用旋转设计图案
解:A、图中利用的是对称,错误;
B、图中利用的是旋转,正确;
C、图中利用的位似,错误;
D、图中利用的是平移,错误;
故选B
分析:根据旋转的性质与特点判断即可.
9. A
考点:旋转的性质,利用旋转设计图案
解:整个图案可以看成是一个正八边形的旋转,至少旋转360°8=45°。
故答案为:A
分析:根据旋转的性质,旋转的角度不变,而整个图案是一个正八边形,即可求出旋转角的度数。
10. C
考点:生活中的平移现象,利用平移设计图案
解:如图,可知断去的小菱形的个数为5个。
分析:根据题意可知断去的菱形个数均为较小的正整数,由所示的图形规律画出完整的装饰链,可得断去部分的小菱形的个数。
二、填空题
11. 2.
考点:利用轴对称设计图案
解:如图所示:
在剩下的13个白色小方格中随意选一个涂成黑色,使得黑色小方格组成的图形为轴对称图形的涂法有2种,
故答案为:2.
分析:把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形,根据定义即可判断出可以涂色的图形.
12. 把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD
考点:利用旋转设计图案
解:观察图形可知把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD.
故答案为:把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD
分析:旋转的性质:①旋转后的每一点都绕着旋转中心,旋转了同样大小的角度;②旋转后的图形与原来图形的形状与大小都没有发生变化,③旋转前后两个图形的对应点到旋转中心的距离相等;④对应点到旋转中心的连线所成的角相等.观察图形,回想正方形的特性; 根据旋转变换图形的性质即可得出答案.
13. 轴对称;旋转;平移
考点:利用轴对称设计图案,利用平移设计图案,利用旋转设计图案
解:图①经过轴对称变换得到图②;图①经过旋转变换得到图③;图①经过平移变换得到图④.
故答案为:轴对称;旋转;平移.
分析:根据轴对称、旋转和平移的定义,直接求解.
14.①④;③;②
考点:利用平移设计图案,利用旋转设计图案
解:可以通过平移变换但不能通过旋转变换得到的图案有①④; 可以通过旋转变换但不能通过平移变换得到的图案有③;既可通过平移变换,又可通过旋转变换得到的图案有②.
故答案为:①④,③,②.
分析:分别根据平移的性质以及旋转的性质进而判断得出即可.
三、解答题
15. 解:图(1)中的图②是由图①经过平移变换而得到;
图(2)中的图②是由图①经过旋转变换而得到(绕点C旋转180°);
图(3)中的图②是由图①经过旋转变换而得到(绕点A旋转180°);
图(4)中的图②是由图①经过轴对称变换而得到(以AC所在的直线为对称轴);
图(5)中的图②是由图①经过旋转变换而得到(绕点B旋转180°)
考点:利用轴对称设计图案,利用平移设计图案,利用旋转设计图案
分析:图(1)中两个图形的方向没有改变,那么是平移得到的,看对应点C的平移即可;图(2)中两个图形的方向改变,那么是旋转得到的,C点位置没有变,是旋转中心,AB和它的对应边在一条直线上,那么旋转角度是180°;
图(3)中两个图形的方向改变,那么是旋转得到的,A点位置没有变,是旋转中心,AB和它的对应边在一条直线上,那么旋转角度是180°;图(4)中各对应点重合,那么是翻折得到的,对应点所在的直线即为对称轴;图(5)中,B点位置没有变,是旋转中心,AB和它的对应边在一条直线上,那么旋转角度是180°.
16.解:先以等边三角形的一边为基础画一个基本图形,再绕等边三角形的两个顶点分别旋转60°后删除原等边三角形.
如图所示:
考点:利用旋转设计图案
分析:利用旋转设计图案,此题答案不唯一,先以等边三角形的一边为基础画一个基本图形,再绕等边三角形的两个顶点分别旋转60°后删除原等边三角形.
17. 解:如图所示.
考点:利用轴对称设计图案
分析:根据轴对称的定义和六边形的性质求解可得.
18. (1)解:如图,即为所求作的轴对称图形。
(2)解:如图,即为所求作的轴对称图形.
考点:利用轴对称设计图案
分析:根据轴对称的图形的定义及题中要求设计即可.
19. (1)都是轴对称图形;都是中心对称图形
(2)解:如图所示,
考点:轴对称图形,利用轴对称设计图案,中心对称及中心对称图形,利用旋转设计图案
解:试题解析:(1)特征1:都是轴对称图形;
特征2:都是中心对称图形,
故答案为:都是轴对称图形;都是中心对称图形;
分析:(1)中心对称图形:把一个图形绕着某一点旋转180°后,如果旋转后的图形能够与原来的图形重合,轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;据此解答即可.
(2)根据(1)中的特征画出图形即可(答案不唯一).
