七年级数学7.2.2三角形的外角
文档属性
| 名称 | 七年级数学7.2.2三角形的外角 |  | |
| 格式 | zip | ||
| 文件大小 | 719.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-16 12:01:16 | ||
图片预览


文档简介
(共27张PPT)
三角形的内角
三角形内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
回顾与思考
A
B
C
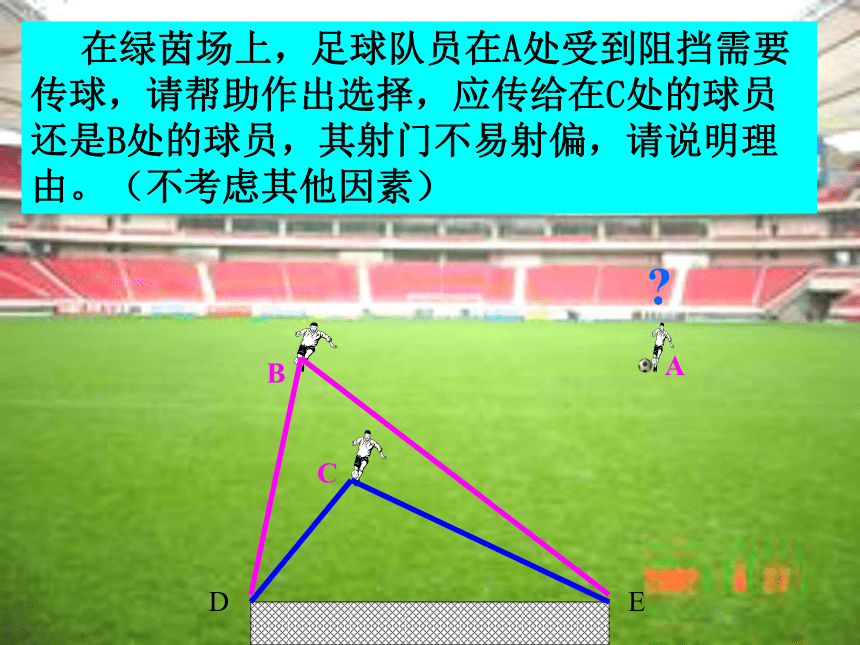
在绿茵场上,足球队员在A处受到阻挡需要传球,请帮助作出选择,应传给在C处的球员还是B处的球员,其射门不易射偏,请说明理由。(不考虑其他因素)
A
B
C
D
E
三角形的外角
A
C
B
D
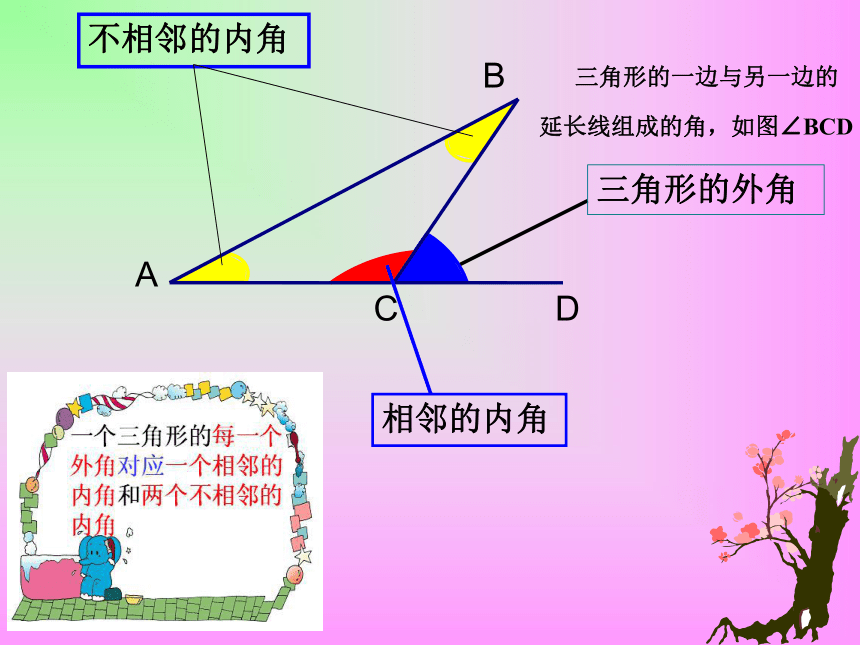
相邻的内角
不相邻的内角
三角形的一边与另一边的
延长线组成的角,如图∠BCD
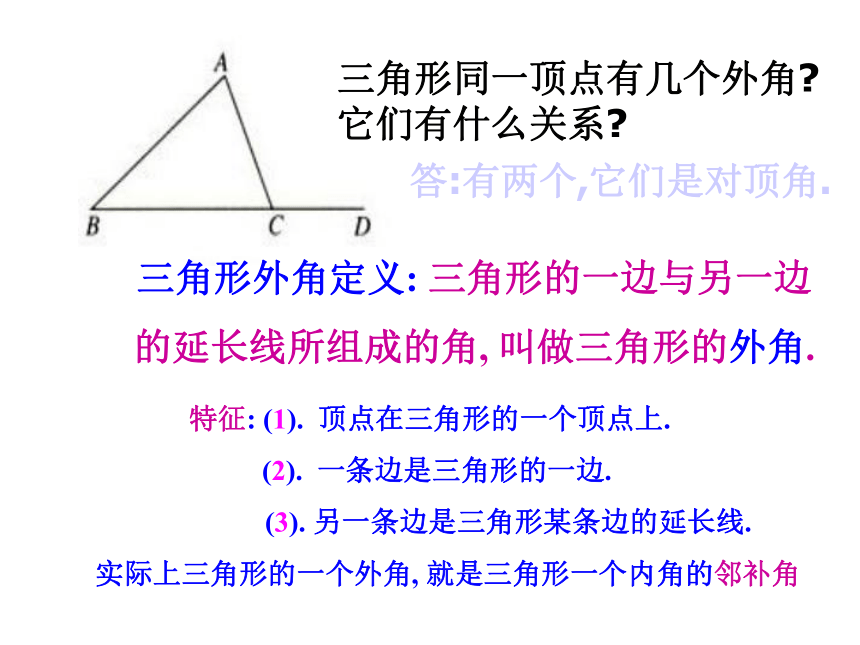
三角形外角定义: 三角形的一边与另一边
的延长线所组成的角, 叫做三角形的外角.
特征: (1). 顶点在三角形的一个顶点上.
(2). 一条边是三角形的一边.
(3). 另一条边是三角形某条边的延长线.
实际上三角形的一个外角, 就是三角形一个内角的邻补角
三角形同一顶点有几个外角
它们有什么关系
答:有两个,它们是对顶角.
A
B
D
E
F
C
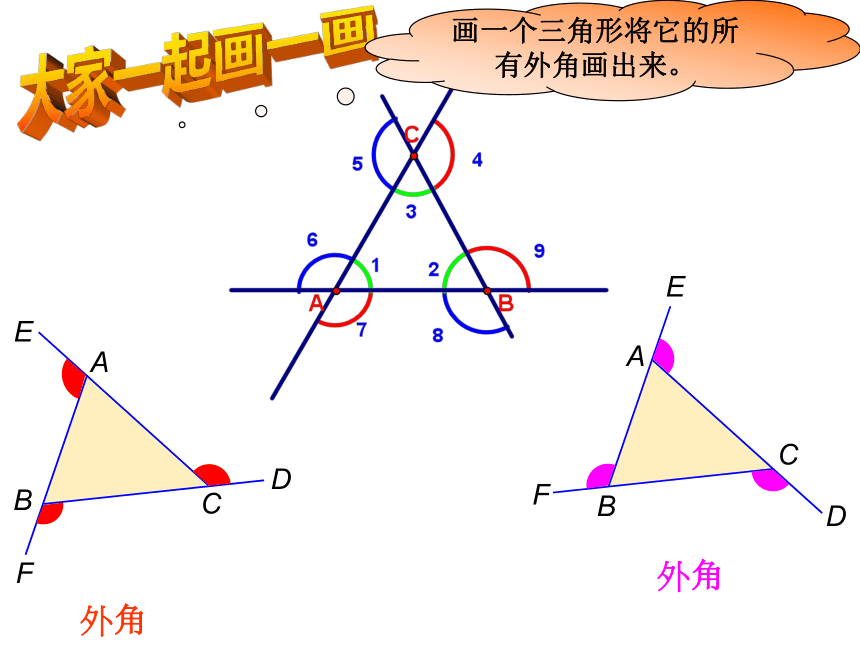
外角
A
B
D
E
F
C
外角
画一个三角形将它的所有外角画出来。
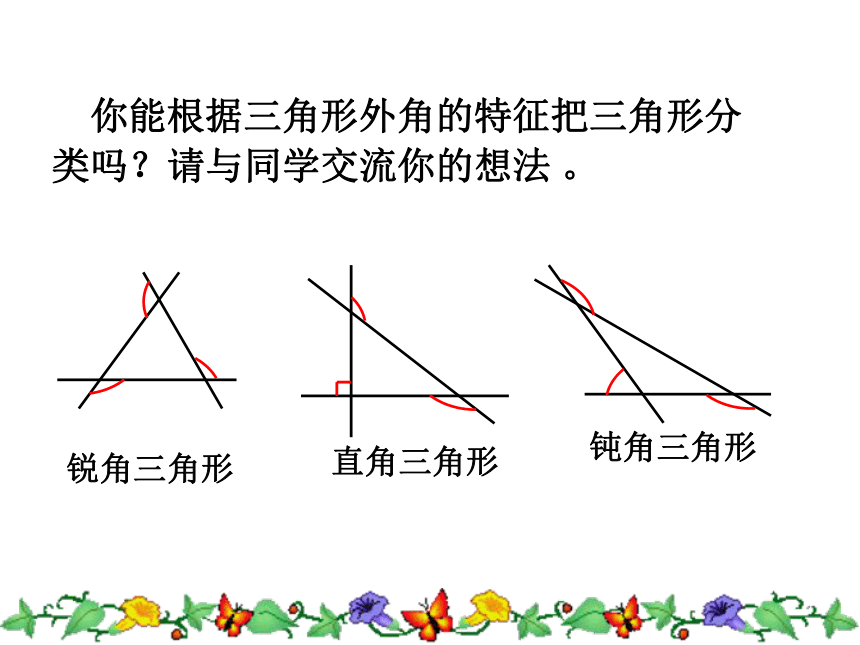
你能根据三角形外角的特征把三角形分类吗?请与同学交流你的想法 。
锐角三角形
直角三角形
钝角三角形
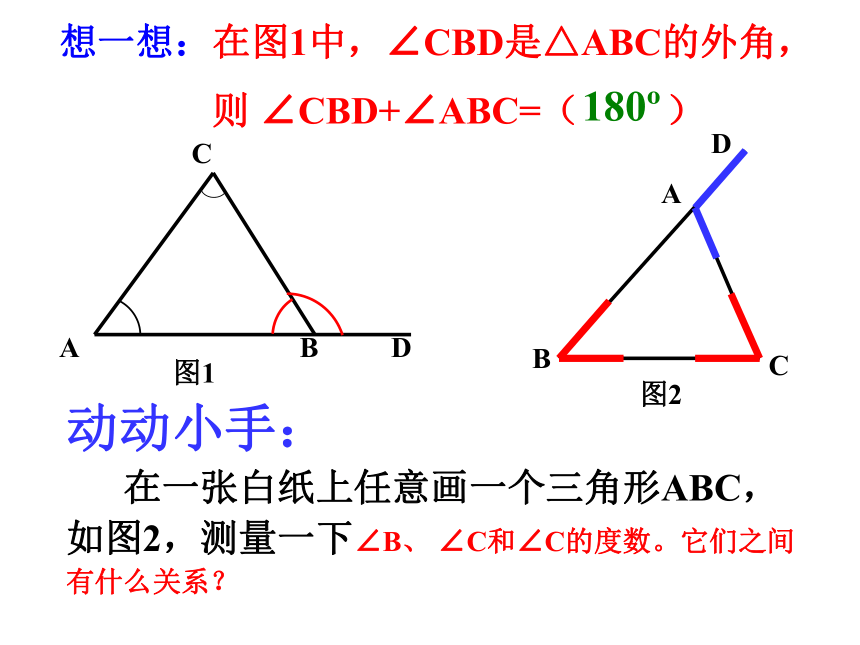
想一想:在图1中,∠CBD是△ABC的外角,
则 ∠CBD+∠ABC=( )
A
B
C
D
图1
180
动动小手:
在一张白纸上任意画一个三角形ABC,如图2,测量一下∠B、 ∠C和∠C的度数。它们之间有什么关系?
A
B
C
D
图2
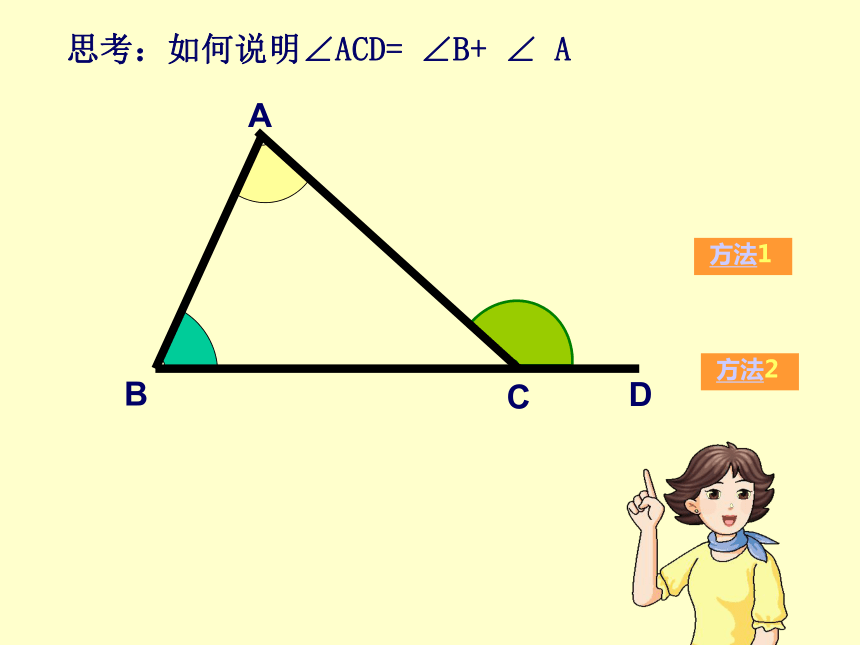
思考:如何说明∠ACD= ∠B+ ∠ A
D
A
B
C
方法1
方法2
D
因为∠ACD+ ∠ACB=180°
又因为∠A+ ∠B+ ∠ACB=180°
所以, ∠A+ ∠B= ∠ACD
解:
A
B
C
所以∠ACD =180 ° -∠ACB
所以∠A+ ∠B =180 ° -∠ACB
(邻补角的定义)
(三角形内角和180 ° )
(等量代换)
1
(CE//BA)
A
E
说一说
擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?
C
B
D
D
解:过C作CE平行于AB
A
B
C
1
2
∴ ∠1= ∠B
(两直线平行,同位角相等)
∠2= ∠A
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B
E
三角形的一个外角等于与它不相邻的两个内角的和
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
结论:三角形的一个外角大于任何一个与它不相邻的内角。
D
A
C
B
>
>
选谁 ?
∠ACD= ∠A+ ∠B
三角形外角的性质:
1、三角形的一个外角等于
与它不相邻的两个内角的
和。 ∠B+∠C=∠CAD
2、三角形的一个外角大于任何
一个与它不相邻的内角。
∠CAD > ∠B, ∠CAD > ∠C
A
B
C
D
90
85
95
60
43
30
求下列各图中∠α的度数。
α
60
30
∠α=( )
α
120
35
∠α=( )
α
45
50
∠α=( )
α
123
80
∠α=( )
α
45
20
35
∠α=( )
α
25
35
∠α=( )
解决引入问题
E
1
因为 ∠ ADB是△ADE的外角
所以 ∠ ADB> ∠ 1
又因为 ∠ 1 是△ECB的外角
所以 ∠ 1 > ∠ C
∠ ADB> ∠ 1 > ∠ C
你会应用吗?
已知∠1、 ∠2 ,∠3是三角形ABC的不同三个外角,
∠1+ ∠2 +∠3=
三角形的三个外角中最多有 锐角,最多有 个钝角,
最多有 个直角
360度
1
3
1
国旗上的数学
A
B
C
D
E
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
A
B
C
D
E
1
2
F
G
解:∵∠1是△FBE的外角
∴∠1=∠B+ ∠E
同理∠2=∠A+∠D
在△CFG中
∠C+∠1+∠2=180
∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180
A
B
C
D
E
1
2
F
4
如图,计算∠BOC
让 我 们 一 起 去 发 现
C
B
O
A
F
C
B
O
A
F
2、这堂课你记忆最深刻的是什么?
1、这堂课你最感兴趣的是什么?
小结:
3、今天你学会了什么?
2、三角形的一个外角的性质
(3)三角形的一个外角大于任何一个与它不相邻的内角。
1、三角形的内角和180°
三角形内角和外角的性质
(1)三角形的一个外角与它相邻内角的关系是互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
3、三角形的外角和等于 360°
三角形的内角
三角形内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
回顾与思考
A
B
C
在绿茵场上,足球队员在A处受到阻挡需要传球,请帮助作出选择,应传给在C处的球员还是B处的球员,其射门不易射偏,请说明理由。(不考虑其他因素)
A
B
C
D
E
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
三角形的一边与另一边的
延长线组成的角,如图∠BCD
三角形外角定义: 三角形的一边与另一边
的延长线所组成的角, 叫做三角形的外角.
特征: (1). 顶点在三角形的一个顶点上.
(2). 一条边是三角形的一边.
(3). 另一条边是三角形某条边的延长线.
实际上三角形的一个外角, 就是三角形一个内角的邻补角
三角形同一顶点有几个外角
它们有什么关系
答:有两个,它们是对顶角.
A
B
D
E
F
C
外角
A
B
D
E
F
C
外角
画一个三角形将它的所有外角画出来。
你能根据三角形外角的特征把三角形分类吗?请与同学交流你的想法 。
锐角三角形
直角三角形
钝角三角形
想一想:在图1中,∠CBD是△ABC的外角,
则 ∠CBD+∠ABC=( )
A
B
C
D
图1
180
动动小手:
在一张白纸上任意画一个三角形ABC,如图2,测量一下∠B、 ∠C和∠C的度数。它们之间有什么关系?
A
B
C
D
图2
思考:如何说明∠ACD= ∠B+ ∠ A
D
A
B
C
方法1
方法2
D
因为∠ACD+ ∠ACB=180°
又因为∠A+ ∠B+ ∠ACB=180°
所以, ∠A+ ∠B= ∠ACD
解:
A
B
C
所以∠ACD =180 ° -∠ACB
所以∠A+ ∠B =180 ° -∠ACB
(邻补角的定义)
(三角形内角和180 ° )
(等量代换)
1
(CE//BA)
A
E
说一说
擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?
C
B
D
D
解:过C作CE平行于AB
A
B
C
1
2
∴ ∠1= ∠B
(两直线平行,同位角相等)
∠2= ∠A
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B
E
三角形的一个外角等于与它不相邻的两个内角的和
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
结论:三角形的一个外角大于任何一个与它不相邻的内角。
D
A
C
B
>
>
选谁 ?
∠ACD= ∠A+ ∠B
三角形外角的性质:
1、三角形的一个外角等于
与它不相邻的两个内角的
和。 ∠B+∠C=∠CAD
2、三角形的一个外角大于任何
一个与它不相邻的内角。
∠CAD > ∠B, ∠CAD > ∠C
A
B
C
D
90
85
95
60
43
30
求下列各图中∠α的度数。
α
60
30
∠α=( )
α
120
35
∠α=( )
α
45
50
∠α=( )
α
123
80
∠α=( )
α
45
20
35
∠α=( )
α
25
35
∠α=( )
解决引入问题
E
1
因为 ∠ ADB是△ADE的外角
所以 ∠ ADB> ∠ 1
又因为 ∠ 1 是△ECB的外角
所以 ∠ 1 > ∠ C
∠ ADB> ∠ 1 > ∠ C
你会应用吗?
已知∠1、 ∠2 ,∠3是三角形ABC的不同三个外角,
∠1+ ∠2 +∠3=
三角形的三个外角中最多有 锐角,最多有 个钝角,
最多有 个直角
360度
1
3
1
国旗上的数学
A
B
C
D
E
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
A
B
C
D
E
1
2
F
G
解:∵∠1是△FBE的外角
∴∠1=∠B+ ∠E
同理∠2=∠A+∠D
在△CFG中
∠C+∠1+∠2=180
∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180
A
B
C
D
E
1
2
F
4
如图,计算∠BOC
让 我 们 一 起 去 发 现
C
B
O
A
F
C
B
O
A
F
2、这堂课你记忆最深刻的是什么?
1、这堂课你最感兴趣的是什么?
小结:
3、今天你学会了什么?
2、三角形的一个外角的性质
(3)三角形的一个外角大于任何一个与它不相邻的内角。
1、三角形的内角和180°
三角形内角和外角的性质
(1)三角形的一个外角与它相邻内角的关系是互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
3、三角形的外角和等于 360°
