人教版数学六年级下册6 整理和复习 4. 数学思考课件(46张PPT)
文档属性
| 名称 | 人教版数学六年级下册6 整理和复习 4. 数学思考课件(46张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 15:46:39 | ||
图片预览





文档简介
4. 数学思考
第1课时 练习(1)
整理和复习
数学六年级下册(RJ) 教学课件
6
一、情景导入
数学家华罗庚说过:“同学们,在解决数学难题时我们要学会知难而“退”,要善于退,足够的退,退到最简单又不失关键的地方。那么,你就已经找到这道题的精髓了。”
(1) 3, 11, 20 ,30, ,53, ,…
?
?
?
(2) ABCD,BCDA,CDAB, , ……
(3)一些小球按下面的方式堆放。
……
41
66
DABC
你知道第5堆有多少个小球?请你画出来。
15个
找规律。
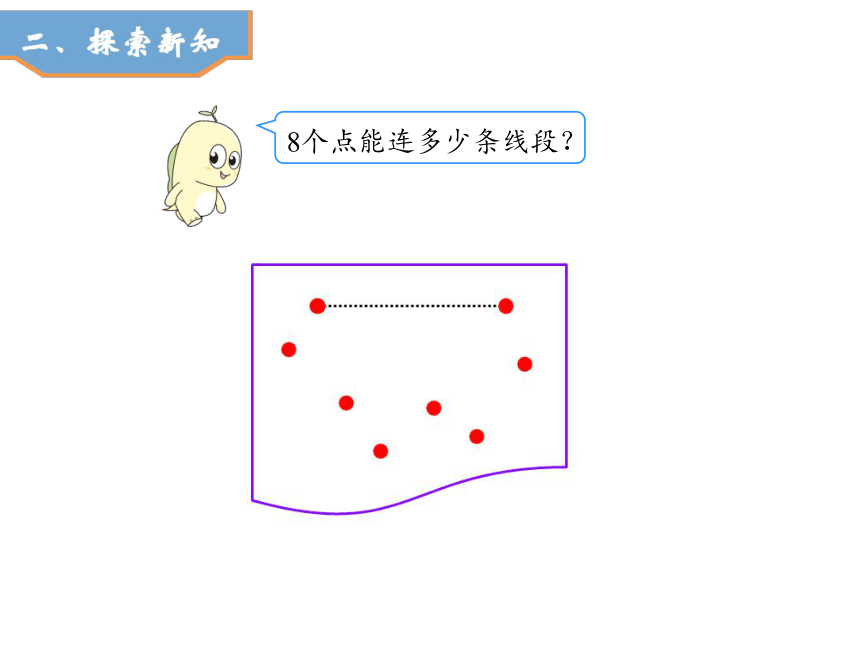
8个点能连多少条线段?
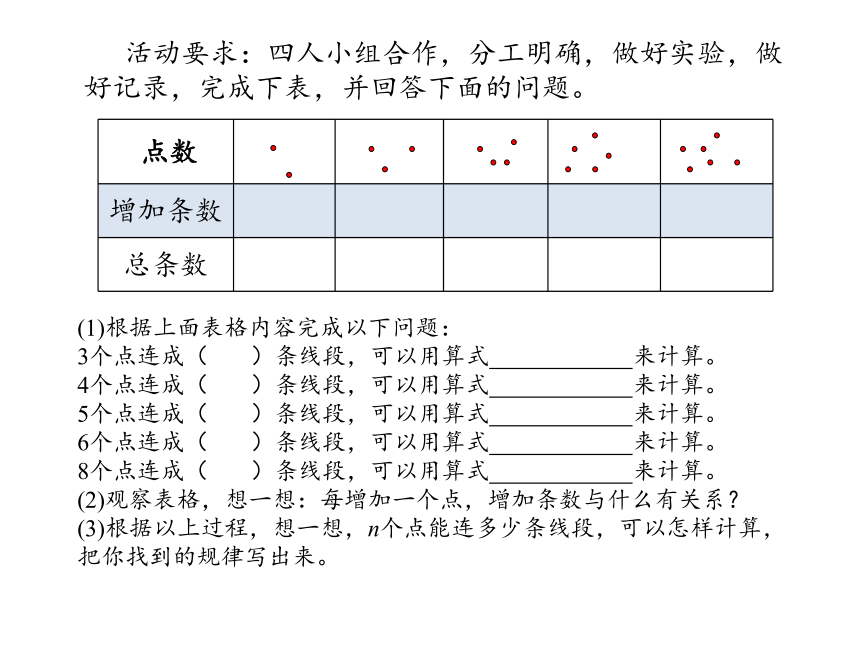
活动要求:四人小组合作,分工明确,做好实验,做好记录,完成下表,并回答下面的问题。
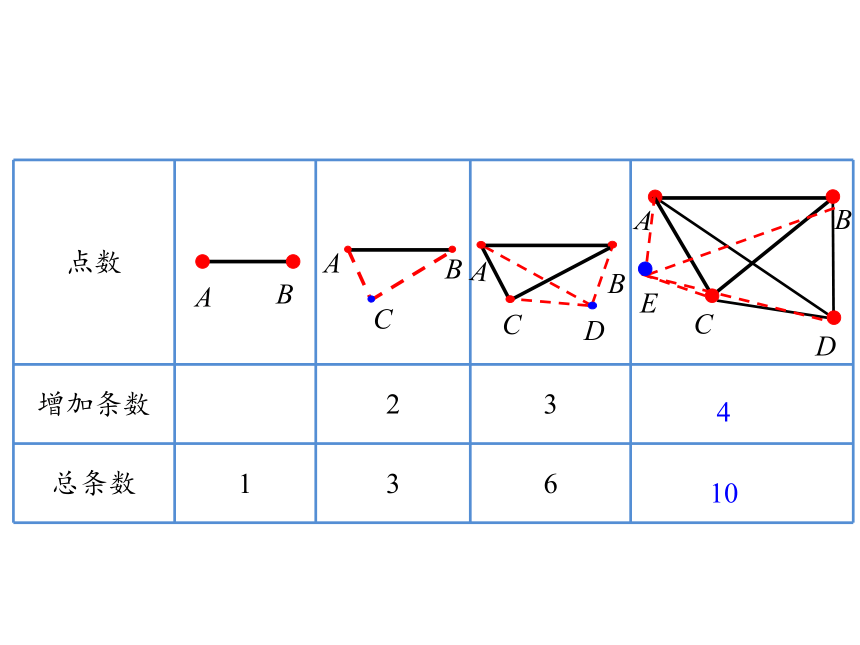
点数
增加条数
总条数
(1)根据上面表格内容完成以下问题:
3个点连成( )条线段,可以用算式 来计算。
4个点连成( )条线段,可以用算式 来计算。
5个点连成( )条线段,可以用算式 来计算。
6个点连成( )条线段,可以用算式 来计算。
8个点连成( )条线段,可以用算式 来计算。
(2)观察表格,想一想:每增加一个点,增加条数与什么有关系?
(3)根据以上过程,想一想,n个点能连多少条线段,可以怎样计算,
把你找到的规律写出来。
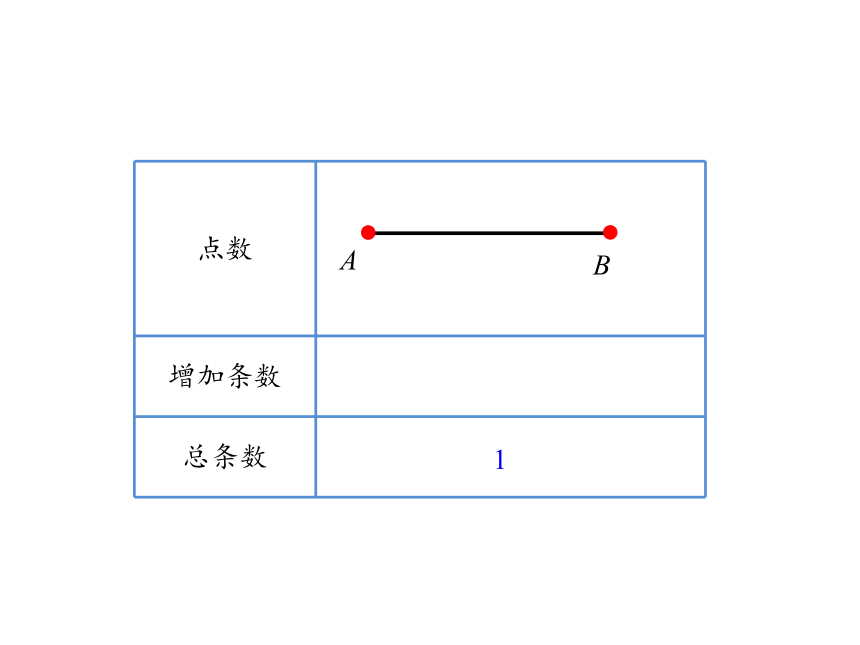
点数
增加条数
总条数
A
B
1
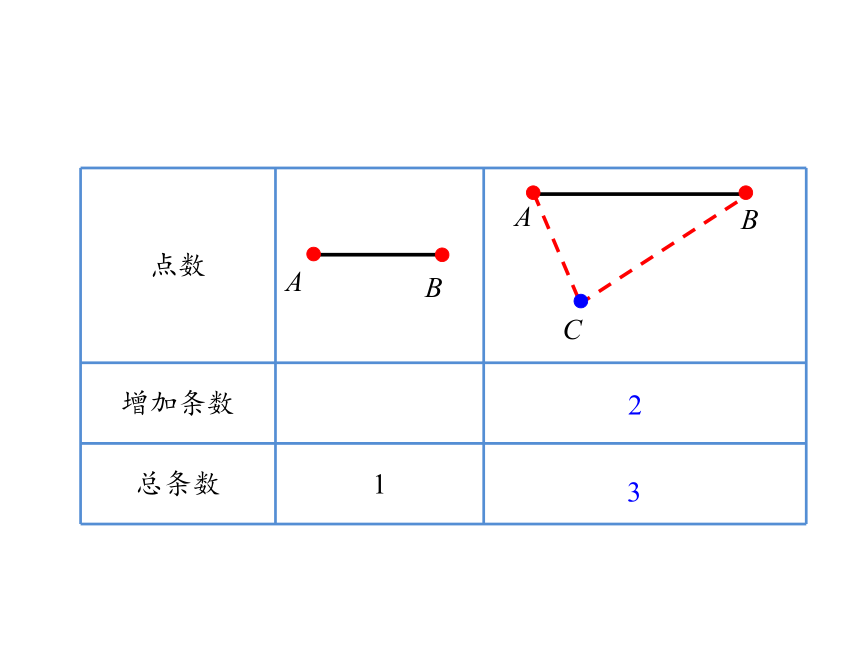
点数
增加条数
总条数
1
A
B
C
2
3
A
B
点数
增加条数
2
总条数
1
3
A
B
C
3
6
D
A
B
A
B
C
点数
增加条数
2
3
总条数
1
3
6
4
10
A
B
C
D
E
A
B
A
B
C
A
B
C
D
C
D
E
A
B
F
5
15
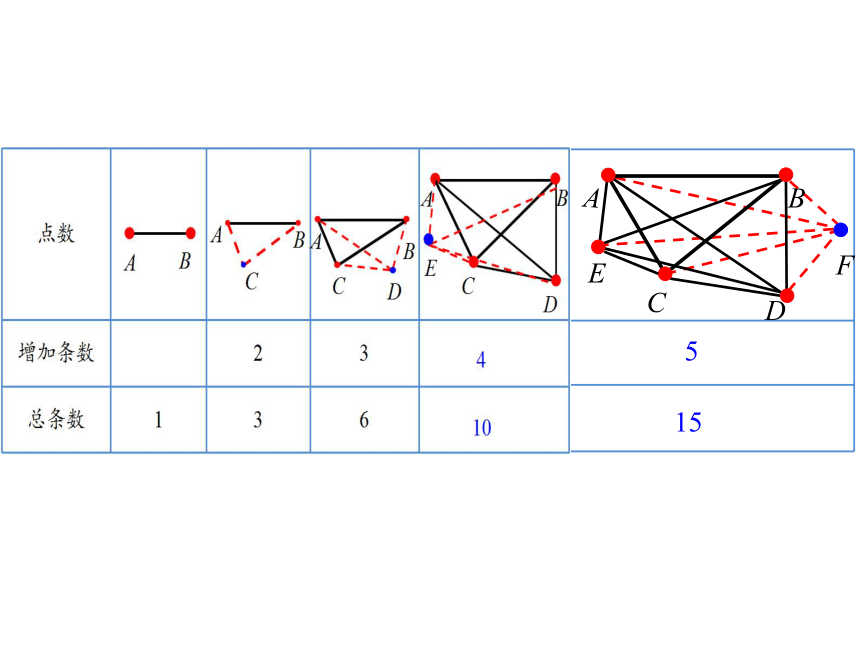
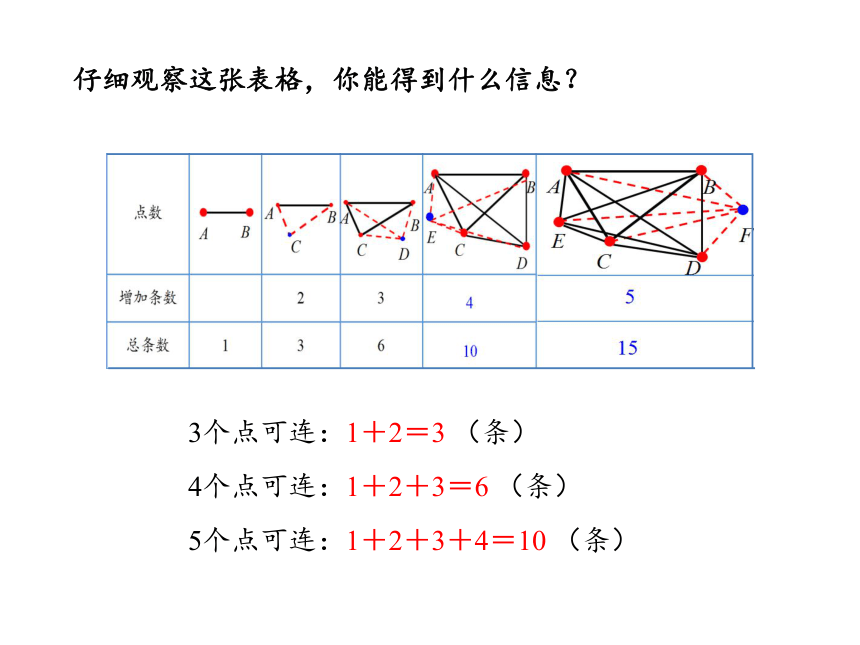
仔细观察这张表格,你能得到什么信息?
3个点可连:1+2=3 (条)
4个点可连:1+2+3=6 (条)
5个点可连:1+2+3+4=10 (条)
12个点可连:
20个点可连:
1+2+3+…+10+11=66(条)
n个点:
1+2+3+ … +(n-1)
1+2+3+…+19=190(条)
8个点可连:
1+2+3+4+5+6+7=28(条)
6个点可连:
1+2+3+4+5=15(条)
三、梯度练习
10个好朋友,每2位好朋友握手1次,大家一共要握手多少次?
1+2+3+…+9=45(次)
(1)第6个图形是什么图形?
(2)摆7个图形需要用多少根小棒?
15根
……
除了第一个图形要3根,其余都只要 2根小棒, 即2n+1。
按规律排列的一串数2、5、10、17、26,…第20个数是(?? )。
A.400???????? B.399????????? C.401??????? D.398
分析:第1个数 12+1=2,
第2个数 22+1=5,
第3个数 32+1=10,……
第20个数 202+1=401。
C
四、课堂小结
你的收获
练习二十二第1、2题。
五、布置作业
数学六年级下册(RJ) 教学课件
谢谢!
4. 数学思考
第2课时 练习(2)
整理和复习
数学六年级下册(RJ) 教学课件
6
一、情景导入
你想怎样解决这个问题?动手试一试吧。
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。
请问:哪两位班长是同班的?
用数字“1” 表示到会,用数字“0”表示没到会。
A
B
C
D
E
F
第一次
1
1
1
0
0
0
第二次
0
1
0
1
1
0
第三次
1
0
0
0
1
1
用列表的方法试一试!
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问哪两位班长是同班的?
第一次到会的情况:
A只可能和D、E或F同班。
第二次到会的情况:
A只可能和D或E同班。
第三次到会的情况:
A只可能和D同班。
A
B
C
D
E
F
第一次
1
1
1
0
0
0
第二次
0
1
0
1
1
0
第三次
1
0
0
0
1
1
A
B
C
D
E
F
第一次
1
1
1
0
0
0
第二次
0
1
0
1
1
0
第三次
1
0
0
0
1
1
A可能和谁是同班? B、C可能和谁是同班呢?
A和D同班, B和F同班, C和E同班。
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问哪两位班长是同班的?
三、梯度练习
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。
请问:他们的职业各是什么?
王阿姨
刘阿姨
丁叔叔
李叔叔
工人
教师
军人
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。
√
×
√
√
×
√
小强、小青、小玲、小红四人中,小强不是最矮的,小红不是最高的,但比小强高,小玲不比大家高。按从高到矮是顺序写出他们的名字是(?? )。
A.小青;小红;小强;小玲
B.小玲;小红;小强;小青
C.小红;小玲;小强;小青
根据“小玲不比大家高”知道小玲最矮;根据“小红不是最高的,但比小强高”小红身高>小强身高,并且小红不是最高,又因为小玲最矮,所以最高的是小青,所以身高顺序是小青身高>小红身高>小强身高>小玲身高。
A
图中有4根绳子,在绳的两端用力拉,有一根绳子是能打成结的,请问是哪一根?( )
A.
B.
C.
D.
分析:假定固定绳子的一头,拉起绳子的另一头,顺着绳子观察,想象是否会出现打结的情况。
B
四、课堂小结
你的收获
练习二十二第7、8题。
五、布置作业
数学六年级下册(RJ) 教学课件
谢谢!
4. 数学思考
第3课时 练习(3)
整理和复习
数学六年级下册(RJ) 教学课件
6
一、情景导入
(1)已知 + =24, = + + 。
求 和 的值。
1. 、 、 、 、 各代表一个数。
圈起来的这一步运用了等量代换的数学思想。
+ = 24
= 6
+
= 24
+
+
=
+
+
=18
2.
+
=
160,
是否等于 ?
+
=
160。
在推理的过程中,运用了等式的性质。
+
=
+
=
-
+
=
+
-
什么是平角?平角与直线有什么区别?
3. 如右图,两条直线相交于点O。
∠1 和∠2 、∠2和∠3 、∠3和∠4 、∠4和∠1,一共能组成4个平角。
(1)每相邻两个角可以组成一个平角,一共能组成几个平角?
(2)你能推出∠1=∠3吗?
∠1+∠2
=
180°
∠2+∠3
=
180°
∠1+∠2
=
∠2+∠3
∠3
∠1
=
=
-∠2
∠1+∠2
∠2+∠3
-∠2
在推理的过程中,运用了等量代换的知识。
+ + =?
三、梯度练习
1. 下面的 、 、 各代表几? 那么 + + =?
+ + =12
+ + =15
+ + =18
+ + =4 + 6 + 5 =15
=4
=6
=5
2. 下面算式中的 、 各代表什么数?
+ + + + + =39
=?
=?
②
①
+ + + + + + + =57
=(39 - 8×3) ÷ 3= 5
=(57-39) ÷ 2 = 8
1. 下面算式中的 图形各代表几?
+ + =36 + + , =?
(1)
+ +6=21- , =?
(2)
(3)
18 × -15 =3 ×7, =?
(4)
6 ×3 -45 ÷ =13 , =?
=36
=2
=5
=9
2. 在三角形ABC中,已知∠A = 30°,∠ABC = 90 °,求∠BCE的度数。
A
B
C
E
∠ACB=180 °-∠A- ∠ABC
=180 °- 30°- 90°
=60 °
∠BCE=180 °-∠ACB
=180 °- 60°
=120 °
已知: ,求 + + + =?
+
1 4 6
当 + =6时, + =14
+ + + =14+6 =20
当 + =16时, + =13
+ + + =13+16 =29
四、课堂小结
你的收获
练习二十二第9、10题。
五、布置作业
数学六年级下册(RJ) 教学课件
谢谢!
第1课时 练习(1)
整理和复习
数学六年级下册(RJ) 教学课件
6
一、情景导入
数学家华罗庚说过:“同学们,在解决数学难题时我们要学会知难而“退”,要善于退,足够的退,退到最简单又不失关键的地方。那么,你就已经找到这道题的精髓了。”
(1) 3, 11, 20 ,30, ,53, ,…
?
?
?
(2) ABCD,BCDA,CDAB, , ……
(3)一些小球按下面的方式堆放。
……
41
66
DABC
你知道第5堆有多少个小球?请你画出来。
15个
找规律。
8个点能连多少条线段?
活动要求:四人小组合作,分工明确,做好实验,做好记录,完成下表,并回答下面的问题。
点数
增加条数
总条数
(1)根据上面表格内容完成以下问题:
3个点连成( )条线段,可以用算式 来计算。
4个点连成( )条线段,可以用算式 来计算。
5个点连成( )条线段,可以用算式 来计算。
6个点连成( )条线段,可以用算式 来计算。
8个点连成( )条线段,可以用算式 来计算。
(2)观察表格,想一想:每增加一个点,增加条数与什么有关系?
(3)根据以上过程,想一想,n个点能连多少条线段,可以怎样计算,
把你找到的规律写出来。
点数
增加条数
总条数
A
B
1
点数
增加条数
总条数
1
A
B
C
2
3
A
B
点数
增加条数
2
总条数
1
3
A
B
C
3
6
D
A
B
A
B
C
点数
增加条数
2
3
总条数
1
3
6
4
10
A
B
C
D
E
A
B
A
B
C
A
B
C
D
C
D
E
A
B
F
5
15
仔细观察这张表格,你能得到什么信息?
3个点可连:1+2=3 (条)
4个点可连:1+2+3=6 (条)
5个点可连:1+2+3+4=10 (条)
12个点可连:
20个点可连:
1+2+3+…+10+11=66(条)
n个点:
1+2+3+ … +(n-1)
1+2+3+…+19=190(条)
8个点可连:
1+2+3+4+5+6+7=28(条)
6个点可连:
1+2+3+4+5=15(条)
三、梯度练习
10个好朋友,每2位好朋友握手1次,大家一共要握手多少次?
1+2+3+…+9=45(次)
(1)第6个图形是什么图形?
(2)摆7个图形需要用多少根小棒?
15根
……
除了第一个图形要3根,其余都只要 2根小棒, 即2n+1。
按规律排列的一串数2、5、10、17、26,…第20个数是(?? )。
A.400???????? B.399????????? C.401??????? D.398
分析:第1个数 12+1=2,
第2个数 22+1=5,
第3个数 32+1=10,……
第20个数 202+1=401。
C
四、课堂小结
你的收获
练习二十二第1、2题。
五、布置作业
数学六年级下册(RJ) 教学课件
谢谢!
4. 数学思考
第2课时 练习(2)
整理和复习
数学六年级下册(RJ) 教学课件
6
一、情景导入
你想怎样解决这个问题?动手试一试吧。
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。
请问:哪两位班长是同班的?
用数字“1” 表示到会,用数字“0”表示没到会。
A
B
C
D
E
F
第一次
1
1
1
0
0
0
第二次
0
1
0
1
1
0
第三次
1
0
0
0
1
1
用列表的方法试一试!
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问哪两位班长是同班的?
第一次到会的情况:
A只可能和D、E或F同班。
第二次到会的情况:
A只可能和D或E同班。
第三次到会的情况:
A只可能和D同班。
A
B
C
D
E
F
第一次
1
1
1
0
0
0
第二次
0
1
0
1
1
0
第三次
1
0
0
0
1
1
A
B
C
D
E
F
第一次
1
1
1
0
0
0
第二次
0
1
0
1
1
0
第三次
1
0
0
0
1
1
A可能和谁是同班? B、C可能和谁是同班呢?
A和D同班, B和F同班, C和E同班。
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问哪两位班长是同班的?
三、梯度练习
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。
请问:他们的职业各是什么?
王阿姨
刘阿姨
丁叔叔
李叔叔
工人
教师
军人
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。
√
×
√
√
×
√
小强、小青、小玲、小红四人中,小强不是最矮的,小红不是最高的,但比小强高,小玲不比大家高。按从高到矮是顺序写出他们的名字是(?? )。
A.小青;小红;小强;小玲
B.小玲;小红;小强;小青
C.小红;小玲;小强;小青
根据“小玲不比大家高”知道小玲最矮;根据“小红不是最高的,但比小强高”小红身高>小强身高,并且小红不是最高,又因为小玲最矮,所以最高的是小青,所以身高顺序是小青身高>小红身高>小强身高>小玲身高。
A
图中有4根绳子,在绳的两端用力拉,有一根绳子是能打成结的,请问是哪一根?( )
A.
B.
C.
D.
分析:假定固定绳子的一头,拉起绳子的另一头,顺着绳子观察,想象是否会出现打结的情况。
B
四、课堂小结
你的收获
练习二十二第7、8题。
五、布置作业
数学六年级下册(RJ) 教学课件
谢谢!
4. 数学思考
第3课时 练习(3)
整理和复习
数学六年级下册(RJ) 教学课件
6
一、情景导入
(1)已知 + =24, = + + 。
求 和 的值。
1. 、 、 、 、 各代表一个数。
圈起来的这一步运用了等量代换的数学思想。
+ = 24
= 6
+
= 24
+
+
=
+
+
=18
2.
+
=
160,
是否等于 ?
+
=
160。
在推理的过程中,运用了等式的性质。
+
=
+
=
-
+
=
+
-
什么是平角?平角与直线有什么区别?
3. 如右图,两条直线相交于点O。
∠1 和∠2 、∠2和∠3 、∠3和∠4 、∠4和∠1,一共能组成4个平角。
(1)每相邻两个角可以组成一个平角,一共能组成几个平角?
(2)你能推出∠1=∠3吗?
∠1+∠2
=
180°
∠2+∠3
=
180°
∠1+∠2
=
∠2+∠3
∠3
∠1
=
=
-∠2
∠1+∠2
∠2+∠3
-∠2
在推理的过程中,运用了等量代换的知识。
+ + =?
三、梯度练习
1. 下面的 、 、 各代表几? 那么 + + =?
+ + =12
+ + =15
+ + =18
+ + =4 + 6 + 5 =15
=4
=6
=5
2. 下面算式中的 、 各代表什么数?
+ + + + + =39
=?
=?
②
①
+ + + + + + + =57
=(39 - 8×3) ÷ 3= 5
=(57-39) ÷ 2 = 8
1. 下面算式中的 图形各代表几?
+ + =36 + + , =?
(1)
+ +6=21- , =?
(2)
(3)
18 × -15 =3 ×7, =?
(4)
6 ×3 -45 ÷ =13 , =?
=36
=2
=5
=9
2. 在三角形ABC中,已知∠A = 30°,∠ABC = 90 °,求∠BCE的度数。
A
B
C
E
∠ACB=180 °-∠A- ∠ABC
=180 °- 30°- 90°
=60 °
∠BCE=180 °-∠ACB
=180 °- 60°
=120 °
已知: ,求 + + + =?
+
1 4 6
当 + =6时, + =14
+ + + =14+6 =20
当 + =16时, + =13
+ + + =13+16 =29
四、课堂小结
你的收获
练习二十二第9、10题。
五、布置作业
数学六年级下册(RJ) 教学课件
谢谢!
