2020-2021学年山东省济宁学院附中九年级(上)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省济宁学院附中九年级(上)期末数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 05:20:30 | ||
图片预览



文档简介
2020-2021学年山东省济宁学院附中九年级第一学期期末数学试卷(五四学制)
一、选择题(共10小题).
1.﹣的倒数为( )
A.﹣6 B. C.6 D.﹣
2.实数﹣,|﹣|,0,中,最小的数是( )
A.﹣ B.|﹣| C.0 D.
3.5G被认为是物联网、自动驾驶汽车、智慧城市的“结缔组织”,是工业互联网的中坚力量.近年来,我国5G发展取得明显成就,根据中国工信部的数据,截至2020年10月底,全国累计建设开通5G基站达69.5万个,将数据69.5万用科学记数法表示为( )
A.695×103 B.69.5×104 C.6.95×105 D.0.695×106
4.下列运算正确的是( )
A.(a3)4=a12 B.a3?a4=a12 C.a2+a2=a4 D.(ab)2=ab2
5.若分式有意义,则x的取值范围是( )
A.x≠0 B.x≠6 C.x≠0且x≠6 D.x≠﹣6
6.在平面直角坐标系中,点M在第四象限,到x轴,y轴的距离分别为6,4,则点M的坐标为( )
A.(4,﹣6) B.(﹣4,6) C.(﹣6,4) D.(﹣6,﹣4)
7.我国古代数学著作《九章算术》“盈不足”一章中记载:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何”.意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛.问1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶盛酒x斛,1个小桶盛酒y斛,下列方程组正确的是( )
A. B.
C. D.
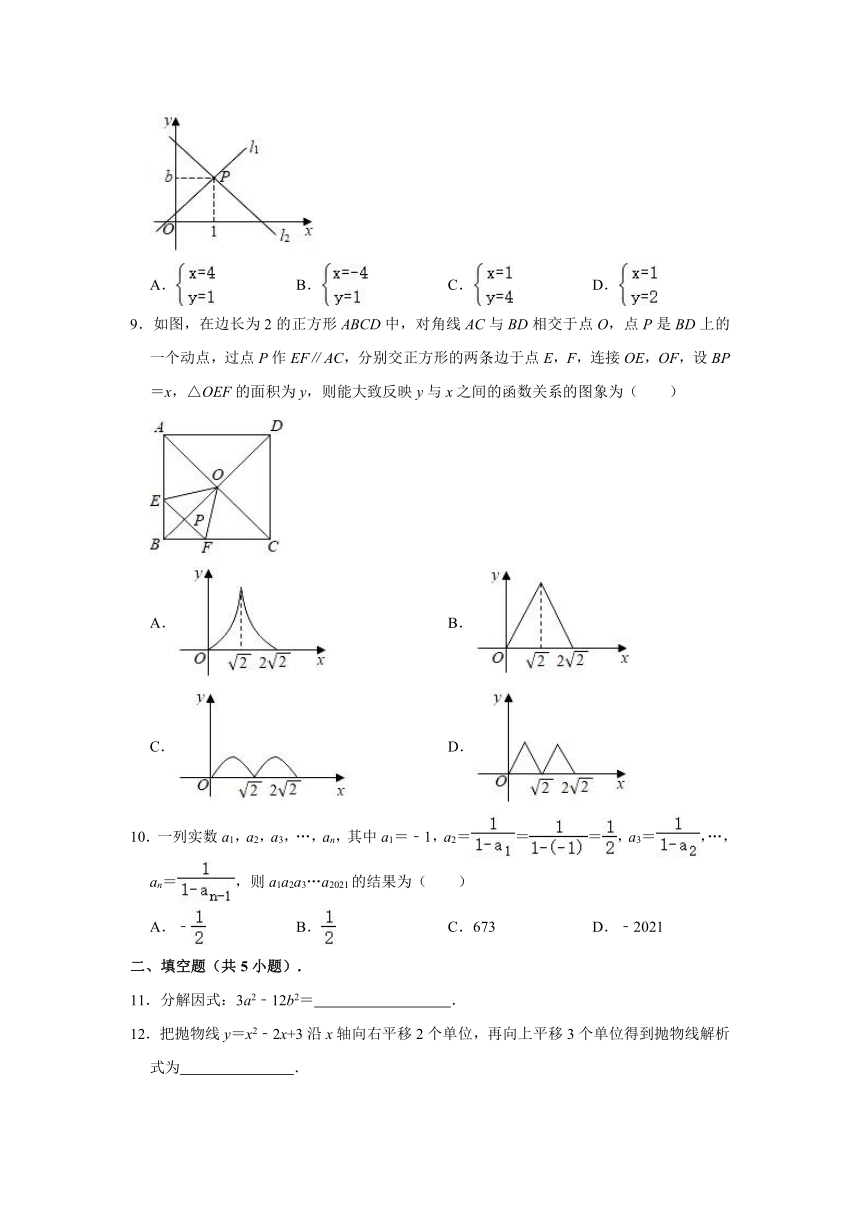
8.如图,直线l1:y=3x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解为( )
A. B. C. D.
9.如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O,点P是BD上的一个动点,过点P作EF∥AC,分别交正方形的两条边于点E,F,连接OE,OF,设BP=x,△OEF的面积为y,则能大致反映y与x之间的函数关系的图象为( )
A. B.
C. D.
10.一列实数a1,a2,a3,…,an,其中a1=﹣1,a2===,a3=,…,an=,则a1a2a3…a2021的结果为( )
A.﹣ B. C.673 D.﹣2021
二、填空题(共5小题).
11.分解因式:3a2﹣12b2= .
12.把抛物线y=x2﹣2x+3沿x轴向右平移2个单位,再向上平移3个单位得到抛物线解析式为 .
13.已知y=++1,= .
14.已知m﹣n=2,则分式÷(2n+)= .
15.如图,在平面直角坐标系中,直线y=x与双曲线y=相交于A、B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP、BC,若△PBC的面积是30,则C点的坐标为 .
三、解答题
16.计算(或解方程):
(1)()0﹣2sin30°++2﹣1;
(2)解方程:x2﹣2x﹣1=0.
17.先化简,再求值:(x+1)2﹣x(x+1),其中x=2.
18.已知关于x的一元二次方程x2﹣(m+2)x+2m=0.
(1)证明:不论m为何值时,方程总有实数根.
(2)若方程的两个实数根x1,x2满足x1+x2﹣x1x2=4,求m的值.
19.如图,直线y=x+m与双曲线y=相交于A(2,1)、B两点.
(1)求m及k的值.
(2)求出S△AOB的面积.
(3)直接写出x+m﹣>0时x的取值范围.
20.某商场准备在济宁义乌批发城采购一批特色商品,经调查,用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A、B型商品的进价分别为多少元?
(2)若该商场购进A、B型商品共160件进行试销,其中A型商品的件数不小于B型的件数,且总成本不能超过24840元,则共有几种进货方案?
(3)已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出,在第(2)问条件下,哪种方案利润最大?并求出最大利润.
21.阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数;
例题:证明当x>0时,函数f(x)=(x>0)是减函数.
证明:设0<x1<x2,则f(x1)﹣f(x2)=﹣==.
∵0<x1<x2
∴x2﹣x1>0,x1x2>0
∴>0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴当x>0时函数f(x)=(x>0)是减函数
根据以上材料,解答下面的问题:
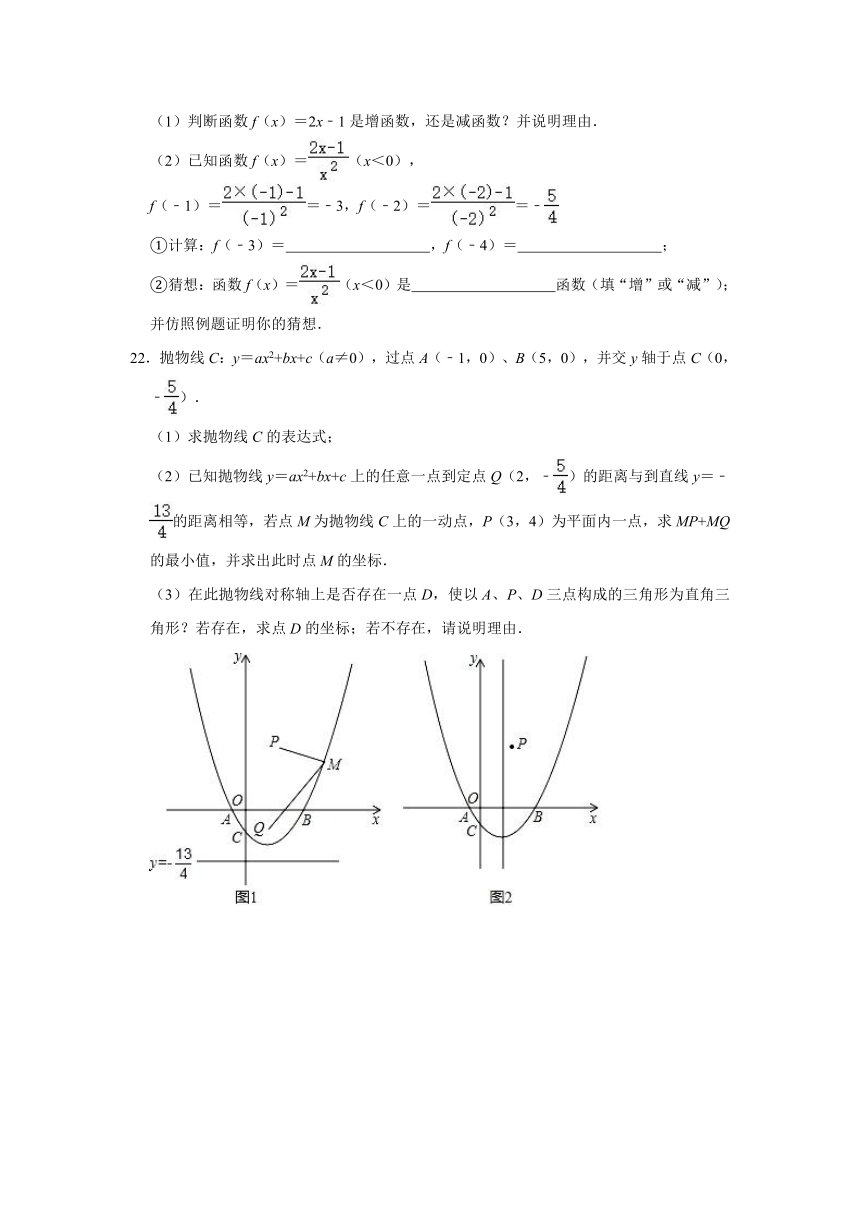
(1)判断函数f(x)=2x﹣1是增函数,还是减函数?并说明理由.
(2)已知函数f(x)=(x<0),
f(﹣1)==﹣3,f(﹣2)==﹣
①计算:f(﹣3)= ,f(﹣4)= ;
②猜想:函数f(x)=(x<0)是 函数(填“增”或“减”);并仿照例题证明你的猜想.
22.抛物线C:y=ax2+bx+c(a≠0),过点A(﹣1,0)、B(5,0),并交y轴于点C(0,﹣).
(1)求抛物线C的表达式;
(2)已知抛物线y=ax2+bx+c上的任意一点到定点Q(2,﹣)的距离与到直线y=﹣的距离相等,若点M为抛物线C上的一动点,P(3,4)为平面内一点,求MP+MQ的最小值,并求出此时点M的坐标.
(3)在此抛物线对称轴上是否存在一点D,使以A、P、D三点构成的三角形为直角三角形?若存在,求点D的坐标;若不存在,请说明理由.
参考答案
一、选择题(共10小题).
1.﹣的倒数为( )
A.﹣6 B. C.6 D.﹣
解:因为﹣×(﹣6)=1,
所以﹣的倒数为﹣6.
故选:A.
2.实数﹣,|﹣|,0,中,最小的数是( )
A.﹣ B.|﹣| C.0 D.
解:∵﹣,|﹣|=,0,=2,
∴实数﹣,|﹣|,0,中,只有﹣是负数,故最小的数是﹣.
故选:A.
3.5G被认为是物联网、自动驾驶汽车、智慧城市的“结缔组织”,是工业互联网的中坚力量.近年来,我国5G发展取得明显成就,根据中国工信部的数据,截至2020年10月底,全国累计建设开通5G基站达69.5万个,将数据69.5万用科学记数法表示为( )
A.695×103 B.69.5×104 C.6.95×105 D.0.695×106
解:69.5万=695000=6.95×105.
故选:C.
4.下列运算正确的是( )
A.(a3)4=a12 B.a3?a4=a12 C.a2+a2=a4 D.(ab)2=ab2
解:A、(a3)4=a12,故原题计算正确;
B、a3?a4=a7,故原题计算错误;
C、a2+a2=2a2,故原题计算错误;
D、(ab)2=a2b2,故原题计算错误;
故选:A.
5.若分式有意义,则x的取值范围是( )
A.x≠0 B.x≠6 C.x≠0且x≠6 D.x≠﹣6
解:要使分式有意义,必须x﹣6≠0,
解得,x≠6,
故选:B.
6.在平面直角坐标系中,点M在第四象限,到x轴,y轴的距离分别为6,4,则点M的坐标为( )
A.(4,﹣6) B.(﹣4,6) C.(﹣6,4) D.(﹣6,﹣4)
解:因为点M在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点M到x轴的距离为6,到y轴的距离为4,
所以点M的坐标为(4,﹣6).
故选:A.
7.我国古代数学著作《九章算术》“盈不足”一章中记载:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何”.意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛.问1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶盛酒x斛,1个小桶盛酒y斛,下列方程组正确的是( )
A. B.
C. D.
解:依题意,得:.
故选:A.
8.如图,直线l1:y=3x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解为( )
A. B. C. D.
解:∵直线y=3x+1经过点P(1,b),
∴b=3+1,
解得b=4,
∴P(1,4),
∴关于x,y的方程组的解为,
故选:C.
9.如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O,点P是BD上的一个动点,过点P作EF∥AC,分别交正方形的两条边于点E,F,连接OE,OF,设BP=x,△OEF的面积为y,则能大致反映y与x之间的函数关系的图象为( )
A. B.
C. D.
解:当点P在OB上时,
∵四边形ABCD是正方形,边长为2,
∴AB=BC=2,AC⊥BD,∠ACB=∠CAB=45°,
∴AC=2,BO=DO=AO=CO=,
∵EF∥AC,
∴∠BAC=∠BEF=45°,∠BFE=∠BCA=45°,∠AOB=∠EPB=90°,
∴∠BEF=∠BFE,
∴BE=BF,
∵∠BPE=90°,
∴BP=EP=FP=x,
∴OP=﹣x,
∴y=×EF×OP=×2x×(﹣x)=﹣x2+x,(0≤x≤)
当点P在DO上时,同理可得:y=﹣x2+3x﹣4,(<x≤2),
故选:C.
10.一列实数a1,a2,a3,…,an,其中a1=﹣1,a2===,a3=,…,an=,则a1a2a3…a2021的结果为( )
A.﹣ B. C.673 D.﹣2021
解:当a1=﹣1,
a2===,
a3===2,
a4==,
…,
所以每3个数一循环;
2021÷3=673…2,
第2020个数是﹣1,
第2021个数是,
(﹣1)××2=﹣1,(﹣1)673=﹣1;
(﹣1)×(﹣1)×=.
故选:B.
二、填空题
11.分解因式:3a2﹣12b2= 3(a+2b)(a﹣2b) .
解:3a2﹣12b2=3(a2﹣4b2)
=3(a+2b)(a﹣2b).
故答案为:3(a+2b)(a﹣2b).
12.把抛物线y=x2﹣2x+3沿x轴向右平移2个单位,再向上平移3个单位得到抛物线解析式为 y=(x﹣3)2+5 .
解:∵y=x2﹣2x+3=(x﹣1)2+2,
∴把抛物线y=x2﹣2x+3沿x轴向右平移2个单位,再向上平移3个单位得到抛物线解析式为:y=(x﹣1﹣2)2+2+3,即y=(x﹣3)2+5.
故答案为y=(x﹣3)2+5.
13.已知y=++1,= 2 .
解:由题意得,x﹣2≥0,2﹣x≥0,
解得,x=2,
则y=1,
∴5x﹣2y=5×2﹣2×1=8,
∵8的立方根是2,
∴=2,
故答案为:2.
14.已知m﹣n=2,则分式÷(2n+)= ﹣ .
解:原式=÷(+)
=÷
=?
=﹣,
当m﹣n=2时,
原式=﹣,
故答案为:﹣.
15.如图,在平面直角坐标系中,直线y=x与双曲线y=相交于A、B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP、BC,若△PBC的面积是30,则C点的坐标为 (7,) .
解:BC交y轴于D,如图,设C点坐标为(a,),
解方程组得或,
∴A点坐标为(2,3),B点坐标为(﹣2,﹣3),
设直线BC的解析式为y=kx+b,
把B(﹣2,﹣3)、C(a,)代入得,解得,
∴直线BC的解析式为y=x+﹣3,
当x=0时,y=x+﹣3=﹣3,
∴D点坐标为(0,﹣3)
设直线AC的解析式为y=mx+n,
把A(2,3)、C(a,)代入得,解得,
∴直线AC的解析式为y=﹣x++3,
当x=0时,y=﹣x++3=+3,
∴P点坐标为(0,+3)
∵S△PBC=S△PBD+S△CPD,
∴×2×6+×a×6=30,解得a=7,
∴C点坐标为(7,).
故答案为(7,).
三、解答题
16.计算(或解方程):
(1)()0﹣2sin30°++2﹣1;
(2)解方程:x2﹣2x﹣1=0.
解:(1)原式=1﹣2×+2+
=1﹣1+2+
=2;
(2)x2﹣2x﹣1=0,
移项,得x2﹣2x=1,
配方,得x2﹣2x+1=1+1,即(x﹣1)2=2,
解得x﹣1=±,
所以x1=1+,x2=1﹣.
17.先化简,再求值:(x+1)2﹣x(x+1),其中x=2.
解:(x+1)2﹣x(x+1)
=x2+2x+1﹣x2﹣x
=x+1,
当x=2时,原式=2+1=3.
18.已知关于x的一元二次方程x2﹣(m+2)x+2m=0.
(1)证明:不论m为何值时,方程总有实数根.
(2)若方程的两个实数根x1,x2满足x1+x2﹣x1x2=4,求m的值.
【解答】(1)证明:∵△=[﹣(m+2)]2﹣4×2m=(m﹣2)2≥0,
∴不论m为何值,该方程总有两个实数根;
(2)解:根据题意得:x1+x2=m+2,x1x2=2m,
∵x1+x2﹣x1x2=4,
∴m+2﹣2m=4.
解得m=﹣2.
19.如图,直线y=x+m与双曲线y=相交于A(2,1)、B两点.
(1)求m及k的值.
(2)求出S△AOB的面积.
(3)直接写出x+m﹣>0时x的取值范围.
解:(1)∵把A(2,1)代入y=x+m得:1=2+m,
∴m=﹣1,
∵把A(2,1)代入y=得:1=,
∴k=2;
(2)解得:,
∴B的坐标是(﹣1,﹣2),
把x=0代入y=x﹣1得y=﹣1,
∴直线与y轴的交点C为(0,﹣1),
∴S△AOB=S△AOC+S△BOC=+=;
(3)由图像可知,x+m﹣>0时x的取值范围是﹣1<x<0或x>2.
20.某商场准备在济宁义乌批发城采购一批特色商品,经调查,用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A、B型商品的进价分别为多少元?
(2)若该商场购进A、B型商品共160件进行试销,其中A型商品的件数不小于B型的件数,且总成本不能超过24840元,则共有几种进货方案?
(3)已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出,在第(2)问条件下,哪种方案利润最大?并求出最大利润.
解:(1)设一件B型商品的进价为x元,则一件A型商品的进价为(x+10)元,
依题意得:=2×,
解得:x=150,
经检验,x=150是原方程的解,且符合题意,
∴x+10=160.
答:一件A型商品的进价为160元,一件B型商品的进价为150元.
(2)设购进A型商品m件,则购进B型商品(160﹣m)件,
依题意得:,
解得:80≤m≤84,
又∵m为整数,
∴m可以为80,81,82,83,84,
∴共有5种进货方案,
方案1:购进80件A型商品,80件B型商品;
方案2:购进81件A型商品,79件B型商品;
方案3:购进82件A型商品,78件B型商品;
方案4:购进83件A型商品,77件B型商品;
方案5:购进84件A型商品,76件B型商品.
(3)方案1可获得的销售利润为(240﹣160)×80+(220﹣150)×80=12000(元);
方案2可获得的销售利润为(240﹣160)×81+(220﹣150)×79=12010(元);
方案3可获得的销售利润为(240﹣160)×82+(220﹣150)×78=12020(元);
方案4可获得的销售利润为(240﹣160)×83+(220﹣150)×77=12030(元);
方案5可获得的销售利润为(240﹣160)×84+(220﹣150)×76=12040(元).
∵12000<12010<12020<12030<12040,
∴购进84件A型商品,76件B型商品时获得的销售利润最大,最大利润为12040元.
21.阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数;
例题:证明当x>0时,函数f(x)=(x>0)是减函数.
证明:设0<x1<x2,则f(x1)﹣f(x2)=﹣==.
∵0<x1<x2
∴x2﹣x1>0,x1x2>0
∴>0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴当x>0时函数f(x)=(x>0)是减函数
根据以上材料,解答下面的问题:
(1)判断函数f(x)=2x﹣1是增函数,还是减函数?并说明理由.
(2)已知函数f(x)=(x<0),
f(﹣1)==﹣3,f(﹣2)==﹣
①计算:f(﹣3)= ﹣ ,f(﹣4)= ﹣ ;
②猜想:函数f(x)=(x<0)是 减 函数(填“增”或“减”);并仿照例题证明你的猜想.
解:(1)函数f(x)=2x﹣1是增函数.
证明:设x1<x2,
f(x1)﹣f(x2)=2x1﹣1﹣(2x2﹣1)=2(x1﹣x2).
∵x1<x2,
∴x1﹣x2<0.
∴f(x1)﹣f(x2)<0.
∴f(x1)<f(x2).
∴函数f(x)=2x﹣1是增函数.
(2)①∵f(x)=(x<0),
∴f(﹣3)==﹣,f(﹣4)==﹣,
故答案为:﹣,﹣;
②猜想:函数f(x)=(x<0)是减函数,
证明:∵﹣4<﹣3,f(﹣4)>f(﹣3),
∴猜想:函数f(x)=(x<0)是减函数,
故答案为减.
22.抛物线C:y=ax2+bx+c(a≠0),过点A(﹣1,0)、B(5,0),并交y轴于点C(0,﹣).
(1)求抛物线C的表达式;
(2)已知抛物线y=ax2+bx+c上的任意一点到定点Q(2,﹣)的距离与到直线y=﹣的距离相等,若点M为抛物线C上的一动点,P(3,4)为平面内一点,求MP+MQ的最小值,并求出此时点M的坐标.
(3)在此抛物线对称轴上是否存在一点D,使以A、P、D三点构成的三角形为直角三角形?若存在,求点D的坐标;若不存在,请说明理由.
解:(1)∵抛物线C:y=ax2+bx+c(a≠0),过点A(﹣1,0)、B(5,0),并交y轴于点C(0,﹣),
∴,
解得:,
∴抛物线C的表达式为:y=x2﹣x﹣;
(2)如图1,作PH⊥直线y=﹣于点H,作MH′⊥直线y=﹣于点H′,
∵抛物线y=ax2+bx+c上的任意一点到定点Q(2,﹣)的距离与到直线y=﹣的距离相等,
∴MQ=MH′,
∴MP+MQ=MP+MH′,当P,M,H′三点在同一条直线上,MP+MH′最小,
∴M与M′重合时,MP+MQ最小,
∵P(3,4),
∴PH=4﹣(﹣)=,
∴MP+MQ的最小值为;
当x=3时,y=×32﹣3﹣=﹣2,
∴M(3,﹣2);
(3)∵y=x2﹣x﹣=y=(x﹣2)2﹣;
∴抛物线对称轴为x=2,
设点坐称为(2,m),
∵A(﹣1,0),P(3,4),D(2,m),
∴AP=4,AD2=9+m2,PD2=1+(m﹣4)2,
∵以A、P、D三点构成的三角形为直角三角形,
∴分三种情况讨论:∠DAP=90°或∠ADP=90°或∠APD=90°
①当∠DAP=90°时,AP2+AD2=PD2,
∴(4)2+9+m2=1+(m﹣4)2,
解得:m=﹣3,
∴D1(2,﹣3);
②当∠ADP=90°时,PD2+AD2=AP2,
∴1+(m﹣4)2+9+m2=(4)2,
解得:m1=2+,m2=2﹣,
∴D2(2,2+);D3(2,2﹣);
③当∠APD=90°时,PD2+AP2=AD2,
∴1+(m﹣4)2+(4)2=9+m2,
解得:m=5,
∴D4(2,5);
综上所述,点D的坐标为(2,﹣3)或(2,2+)或(2,2﹣)或(2,5).
一、选择题(共10小题).
1.﹣的倒数为( )
A.﹣6 B. C.6 D.﹣
2.实数﹣,|﹣|,0,中,最小的数是( )
A.﹣ B.|﹣| C.0 D.
3.5G被认为是物联网、自动驾驶汽车、智慧城市的“结缔组织”,是工业互联网的中坚力量.近年来,我国5G发展取得明显成就,根据中国工信部的数据,截至2020年10月底,全国累计建设开通5G基站达69.5万个,将数据69.5万用科学记数法表示为( )
A.695×103 B.69.5×104 C.6.95×105 D.0.695×106
4.下列运算正确的是( )
A.(a3)4=a12 B.a3?a4=a12 C.a2+a2=a4 D.(ab)2=ab2
5.若分式有意义,则x的取值范围是( )
A.x≠0 B.x≠6 C.x≠0且x≠6 D.x≠﹣6
6.在平面直角坐标系中,点M在第四象限,到x轴,y轴的距离分别为6,4,则点M的坐标为( )
A.(4,﹣6) B.(﹣4,6) C.(﹣6,4) D.(﹣6,﹣4)
7.我国古代数学著作《九章算术》“盈不足”一章中记载:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何”.意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛.问1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶盛酒x斛,1个小桶盛酒y斛,下列方程组正确的是( )
A. B.
C. D.
8.如图,直线l1:y=3x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解为( )
A. B. C. D.
9.如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O,点P是BD上的一个动点,过点P作EF∥AC,分别交正方形的两条边于点E,F,连接OE,OF,设BP=x,△OEF的面积为y,则能大致反映y与x之间的函数关系的图象为( )
A. B.
C. D.
10.一列实数a1,a2,a3,…,an,其中a1=﹣1,a2===,a3=,…,an=,则a1a2a3…a2021的结果为( )
A.﹣ B. C.673 D.﹣2021
二、填空题(共5小题).
11.分解因式:3a2﹣12b2= .
12.把抛物线y=x2﹣2x+3沿x轴向右平移2个单位,再向上平移3个单位得到抛物线解析式为 .
13.已知y=++1,= .
14.已知m﹣n=2,则分式÷(2n+)= .
15.如图,在平面直角坐标系中,直线y=x与双曲线y=相交于A、B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP、BC,若△PBC的面积是30,则C点的坐标为 .
三、解答题
16.计算(或解方程):
(1)()0﹣2sin30°++2﹣1;
(2)解方程:x2﹣2x﹣1=0.
17.先化简,再求值:(x+1)2﹣x(x+1),其中x=2.
18.已知关于x的一元二次方程x2﹣(m+2)x+2m=0.
(1)证明:不论m为何值时,方程总有实数根.
(2)若方程的两个实数根x1,x2满足x1+x2﹣x1x2=4,求m的值.
19.如图,直线y=x+m与双曲线y=相交于A(2,1)、B两点.
(1)求m及k的值.
(2)求出S△AOB的面积.
(3)直接写出x+m﹣>0时x的取值范围.
20.某商场准备在济宁义乌批发城采购一批特色商品,经调查,用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A、B型商品的进价分别为多少元?
(2)若该商场购进A、B型商品共160件进行试销,其中A型商品的件数不小于B型的件数,且总成本不能超过24840元,则共有几种进货方案?
(3)已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出,在第(2)问条件下,哪种方案利润最大?并求出最大利润.
21.阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数;
例题:证明当x>0时,函数f(x)=(x>0)是减函数.
证明:设0<x1<x2,则f(x1)﹣f(x2)=﹣==.
∵0<x1<x2
∴x2﹣x1>0,x1x2>0
∴>0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴当x>0时函数f(x)=(x>0)是减函数
根据以上材料,解答下面的问题:
(1)判断函数f(x)=2x﹣1是增函数,还是减函数?并说明理由.
(2)已知函数f(x)=(x<0),
f(﹣1)==﹣3,f(﹣2)==﹣
①计算:f(﹣3)= ,f(﹣4)= ;
②猜想:函数f(x)=(x<0)是 函数(填“增”或“减”);并仿照例题证明你的猜想.
22.抛物线C:y=ax2+bx+c(a≠0),过点A(﹣1,0)、B(5,0),并交y轴于点C(0,﹣).
(1)求抛物线C的表达式;
(2)已知抛物线y=ax2+bx+c上的任意一点到定点Q(2,﹣)的距离与到直线y=﹣的距离相等,若点M为抛物线C上的一动点,P(3,4)为平面内一点,求MP+MQ的最小值,并求出此时点M的坐标.
(3)在此抛物线对称轴上是否存在一点D,使以A、P、D三点构成的三角形为直角三角形?若存在,求点D的坐标;若不存在,请说明理由.
参考答案
一、选择题(共10小题).
1.﹣的倒数为( )
A.﹣6 B. C.6 D.﹣
解:因为﹣×(﹣6)=1,
所以﹣的倒数为﹣6.
故选:A.
2.实数﹣,|﹣|,0,中,最小的数是( )
A.﹣ B.|﹣| C.0 D.
解:∵﹣,|﹣|=,0,=2,
∴实数﹣,|﹣|,0,中,只有﹣是负数,故最小的数是﹣.
故选:A.
3.5G被认为是物联网、自动驾驶汽车、智慧城市的“结缔组织”,是工业互联网的中坚力量.近年来,我国5G发展取得明显成就,根据中国工信部的数据,截至2020年10月底,全国累计建设开通5G基站达69.5万个,将数据69.5万用科学记数法表示为( )
A.695×103 B.69.5×104 C.6.95×105 D.0.695×106
解:69.5万=695000=6.95×105.
故选:C.
4.下列运算正确的是( )
A.(a3)4=a12 B.a3?a4=a12 C.a2+a2=a4 D.(ab)2=ab2
解:A、(a3)4=a12,故原题计算正确;
B、a3?a4=a7,故原题计算错误;
C、a2+a2=2a2,故原题计算错误;
D、(ab)2=a2b2,故原题计算错误;
故选:A.
5.若分式有意义,则x的取值范围是( )
A.x≠0 B.x≠6 C.x≠0且x≠6 D.x≠﹣6
解:要使分式有意义,必须x﹣6≠0,
解得,x≠6,
故选:B.
6.在平面直角坐标系中,点M在第四象限,到x轴,y轴的距离分别为6,4,则点M的坐标为( )
A.(4,﹣6) B.(﹣4,6) C.(﹣6,4) D.(﹣6,﹣4)
解:因为点M在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点M到x轴的距离为6,到y轴的距离为4,
所以点M的坐标为(4,﹣6).
故选:A.
7.我国古代数学著作《九章算术》“盈不足”一章中记载:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何”.意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛.问1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶盛酒x斛,1个小桶盛酒y斛,下列方程组正确的是( )
A. B.
C. D.
解:依题意,得:.
故选:A.
8.如图,直线l1:y=3x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解为( )
A. B. C. D.
解:∵直线y=3x+1经过点P(1,b),
∴b=3+1,
解得b=4,
∴P(1,4),
∴关于x,y的方程组的解为,
故选:C.
9.如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O,点P是BD上的一个动点,过点P作EF∥AC,分别交正方形的两条边于点E,F,连接OE,OF,设BP=x,△OEF的面积为y,则能大致反映y与x之间的函数关系的图象为( )
A. B.
C. D.
解:当点P在OB上时,
∵四边形ABCD是正方形,边长为2,
∴AB=BC=2,AC⊥BD,∠ACB=∠CAB=45°,
∴AC=2,BO=DO=AO=CO=,
∵EF∥AC,
∴∠BAC=∠BEF=45°,∠BFE=∠BCA=45°,∠AOB=∠EPB=90°,
∴∠BEF=∠BFE,
∴BE=BF,
∵∠BPE=90°,
∴BP=EP=FP=x,
∴OP=﹣x,
∴y=×EF×OP=×2x×(﹣x)=﹣x2+x,(0≤x≤)
当点P在DO上时,同理可得:y=﹣x2+3x﹣4,(<x≤2),
故选:C.
10.一列实数a1,a2,a3,…,an,其中a1=﹣1,a2===,a3=,…,an=,则a1a2a3…a2021的结果为( )
A.﹣ B. C.673 D.﹣2021
解:当a1=﹣1,
a2===,
a3===2,
a4==,
…,
所以每3个数一循环;
2021÷3=673…2,
第2020个数是﹣1,
第2021个数是,
(﹣1)××2=﹣1,(﹣1)673=﹣1;
(﹣1)×(﹣1)×=.
故选:B.
二、填空题
11.分解因式:3a2﹣12b2= 3(a+2b)(a﹣2b) .
解:3a2﹣12b2=3(a2﹣4b2)
=3(a+2b)(a﹣2b).
故答案为:3(a+2b)(a﹣2b).
12.把抛物线y=x2﹣2x+3沿x轴向右平移2个单位,再向上平移3个单位得到抛物线解析式为 y=(x﹣3)2+5 .
解:∵y=x2﹣2x+3=(x﹣1)2+2,
∴把抛物线y=x2﹣2x+3沿x轴向右平移2个单位,再向上平移3个单位得到抛物线解析式为:y=(x﹣1﹣2)2+2+3,即y=(x﹣3)2+5.
故答案为y=(x﹣3)2+5.
13.已知y=++1,= 2 .
解:由题意得,x﹣2≥0,2﹣x≥0,
解得,x=2,
则y=1,
∴5x﹣2y=5×2﹣2×1=8,
∵8的立方根是2,
∴=2,
故答案为:2.
14.已知m﹣n=2,则分式÷(2n+)= ﹣ .
解:原式=÷(+)
=÷
=?
=﹣,
当m﹣n=2时,
原式=﹣,
故答案为:﹣.
15.如图,在平面直角坐标系中,直线y=x与双曲线y=相交于A、B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP、BC,若△PBC的面积是30,则C点的坐标为 (7,) .
解:BC交y轴于D,如图,设C点坐标为(a,),
解方程组得或,
∴A点坐标为(2,3),B点坐标为(﹣2,﹣3),
设直线BC的解析式为y=kx+b,
把B(﹣2,﹣3)、C(a,)代入得,解得,
∴直线BC的解析式为y=x+﹣3,
当x=0时,y=x+﹣3=﹣3,
∴D点坐标为(0,﹣3)
设直线AC的解析式为y=mx+n,
把A(2,3)、C(a,)代入得,解得,
∴直线AC的解析式为y=﹣x++3,
当x=0时,y=﹣x++3=+3,
∴P点坐标为(0,+3)
∵S△PBC=S△PBD+S△CPD,
∴×2×6+×a×6=30,解得a=7,
∴C点坐标为(7,).
故答案为(7,).
三、解答题
16.计算(或解方程):
(1)()0﹣2sin30°++2﹣1;
(2)解方程:x2﹣2x﹣1=0.
解:(1)原式=1﹣2×+2+
=1﹣1+2+
=2;
(2)x2﹣2x﹣1=0,
移项,得x2﹣2x=1,
配方,得x2﹣2x+1=1+1,即(x﹣1)2=2,
解得x﹣1=±,
所以x1=1+,x2=1﹣.
17.先化简,再求值:(x+1)2﹣x(x+1),其中x=2.
解:(x+1)2﹣x(x+1)
=x2+2x+1﹣x2﹣x
=x+1,
当x=2时,原式=2+1=3.
18.已知关于x的一元二次方程x2﹣(m+2)x+2m=0.
(1)证明:不论m为何值时,方程总有实数根.
(2)若方程的两个实数根x1,x2满足x1+x2﹣x1x2=4,求m的值.
【解答】(1)证明:∵△=[﹣(m+2)]2﹣4×2m=(m﹣2)2≥0,
∴不论m为何值,该方程总有两个实数根;
(2)解:根据题意得:x1+x2=m+2,x1x2=2m,
∵x1+x2﹣x1x2=4,
∴m+2﹣2m=4.
解得m=﹣2.
19.如图,直线y=x+m与双曲线y=相交于A(2,1)、B两点.
(1)求m及k的值.
(2)求出S△AOB的面积.
(3)直接写出x+m﹣>0时x的取值范围.
解:(1)∵把A(2,1)代入y=x+m得:1=2+m,
∴m=﹣1,
∵把A(2,1)代入y=得:1=,
∴k=2;
(2)解得:,
∴B的坐标是(﹣1,﹣2),
把x=0代入y=x﹣1得y=﹣1,
∴直线与y轴的交点C为(0,﹣1),
∴S△AOB=S△AOC+S△BOC=+=;
(3)由图像可知,x+m﹣>0时x的取值范围是﹣1<x<0或x>2.
20.某商场准备在济宁义乌批发城采购一批特色商品,经调查,用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A、B型商品的进价分别为多少元?
(2)若该商场购进A、B型商品共160件进行试销,其中A型商品的件数不小于B型的件数,且总成本不能超过24840元,则共有几种进货方案?
(3)已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出,在第(2)问条件下,哪种方案利润最大?并求出最大利润.
解:(1)设一件B型商品的进价为x元,则一件A型商品的进价为(x+10)元,
依题意得:=2×,
解得:x=150,
经检验,x=150是原方程的解,且符合题意,
∴x+10=160.
答:一件A型商品的进价为160元,一件B型商品的进价为150元.
(2)设购进A型商品m件,则购进B型商品(160﹣m)件,
依题意得:,
解得:80≤m≤84,
又∵m为整数,
∴m可以为80,81,82,83,84,
∴共有5种进货方案,
方案1:购进80件A型商品,80件B型商品;
方案2:购进81件A型商品,79件B型商品;
方案3:购进82件A型商品,78件B型商品;
方案4:购进83件A型商品,77件B型商品;
方案5:购进84件A型商品,76件B型商品.
(3)方案1可获得的销售利润为(240﹣160)×80+(220﹣150)×80=12000(元);
方案2可获得的销售利润为(240﹣160)×81+(220﹣150)×79=12010(元);
方案3可获得的销售利润为(240﹣160)×82+(220﹣150)×78=12020(元);
方案4可获得的销售利润为(240﹣160)×83+(220﹣150)×77=12030(元);
方案5可获得的销售利润为(240﹣160)×84+(220﹣150)×76=12040(元).
∵12000<12010<12020<12030<12040,
∴购进84件A型商品,76件B型商品时获得的销售利润最大,最大利润为12040元.
21.阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数;
例题:证明当x>0时,函数f(x)=(x>0)是减函数.
证明:设0<x1<x2,则f(x1)﹣f(x2)=﹣==.
∵0<x1<x2
∴x2﹣x1>0,x1x2>0
∴>0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴当x>0时函数f(x)=(x>0)是减函数
根据以上材料,解答下面的问题:
(1)判断函数f(x)=2x﹣1是增函数,还是减函数?并说明理由.
(2)已知函数f(x)=(x<0),
f(﹣1)==﹣3,f(﹣2)==﹣
①计算:f(﹣3)= ﹣ ,f(﹣4)= ﹣ ;
②猜想:函数f(x)=(x<0)是 减 函数(填“增”或“减”);并仿照例题证明你的猜想.
解:(1)函数f(x)=2x﹣1是增函数.
证明:设x1<x2,
f(x1)﹣f(x2)=2x1﹣1﹣(2x2﹣1)=2(x1﹣x2).
∵x1<x2,
∴x1﹣x2<0.
∴f(x1)﹣f(x2)<0.
∴f(x1)<f(x2).
∴函数f(x)=2x﹣1是增函数.
(2)①∵f(x)=(x<0),
∴f(﹣3)==﹣,f(﹣4)==﹣,
故答案为:﹣,﹣;
②猜想:函数f(x)=(x<0)是减函数,
证明:∵﹣4<﹣3,f(﹣4)>f(﹣3),
∴猜想:函数f(x)=(x<0)是减函数,
故答案为减.
22.抛物线C:y=ax2+bx+c(a≠0),过点A(﹣1,0)、B(5,0),并交y轴于点C(0,﹣).
(1)求抛物线C的表达式;
(2)已知抛物线y=ax2+bx+c上的任意一点到定点Q(2,﹣)的距离与到直线y=﹣的距离相等,若点M为抛物线C上的一动点,P(3,4)为平面内一点,求MP+MQ的最小值,并求出此时点M的坐标.
(3)在此抛物线对称轴上是否存在一点D,使以A、P、D三点构成的三角形为直角三角形?若存在,求点D的坐标;若不存在,请说明理由.
解:(1)∵抛物线C:y=ax2+bx+c(a≠0),过点A(﹣1,0)、B(5,0),并交y轴于点C(0,﹣),
∴,
解得:,
∴抛物线C的表达式为:y=x2﹣x﹣;
(2)如图1,作PH⊥直线y=﹣于点H,作MH′⊥直线y=﹣于点H′,
∵抛物线y=ax2+bx+c上的任意一点到定点Q(2,﹣)的距离与到直线y=﹣的距离相等,
∴MQ=MH′,
∴MP+MQ=MP+MH′,当P,M,H′三点在同一条直线上,MP+MH′最小,
∴M与M′重合时,MP+MQ最小,
∵P(3,4),
∴PH=4﹣(﹣)=,
∴MP+MQ的最小值为;
当x=3时,y=×32﹣3﹣=﹣2,
∴M(3,﹣2);
(3)∵y=x2﹣x﹣=y=(x﹣2)2﹣;
∴抛物线对称轴为x=2,
设点坐称为(2,m),
∵A(﹣1,0),P(3,4),D(2,m),
∴AP=4,AD2=9+m2,PD2=1+(m﹣4)2,
∵以A、P、D三点构成的三角形为直角三角形,
∴分三种情况讨论:∠DAP=90°或∠ADP=90°或∠APD=90°
①当∠DAP=90°时,AP2+AD2=PD2,
∴(4)2+9+m2=1+(m﹣4)2,
解得:m=﹣3,
∴D1(2,﹣3);
②当∠ADP=90°时,PD2+AD2=AP2,
∴1+(m﹣4)2+9+m2=(4)2,
解得:m1=2+,m2=2﹣,
∴D2(2,2+);D3(2,2﹣);
③当∠APD=90°时,PD2+AP2=AD2,
∴1+(m﹣4)2+(4)2=9+m2,
解得:m=5,
∴D4(2,5);
综上所述,点D的坐标为(2,﹣3)或(2,2+)或(2,2﹣)或(2,5).
同课章节目录
