6.1分类加法计数原理与分步乘法计数原理-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册练习(含答案)
文档属性
| 名称 | 6.1分类加法计数原理与分步乘法计数原理-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 738.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 09:36:39 | ||
图片预览




文档简介
6.1分类加法计数原理与分步乘法计数原理
第I卷(选择题)
一、单选题
1.古希腊哲学家毕达哥拉斯曾说过:“美的线型和其他一切美的形体都必须有对称形式”.在中华传统文化里,建筑、器物、书法、诗歌、对联、绘画几乎无不讲究对称之美.如清代诗人黄柏权的《茶壶回文诗》(如图)以连环诗的形式展现,20个字绕着茶壶成一圆环,不论顺着读还是逆着读,皆成佳作.数学与生活也有许多奇妙的联系,如2020年02月02日(20200202)被称为世界完全对称日(公历纪年日期中数字左右完全对称的日期).数学上把20200202这样的对称数叫回文数,如两位数的回文数共有9个(11,22,…,99),则在所有四位数的回文数中,出现奇数的概率为( )
A.false B.false C.false D.false
2.植树节那天,有4名同学植树,现有3棵不同种类的树.若一棵树限1人完成,则不同的分配方法有( )
A.6种 B.3种
C.81种 D.64种
3.若false,且false,则满足条件的不同的有序自然数对false的个数是( )
A.15 B.12
C.5 D.4
4.第七届世界军运会于2019年10月18日至27日在中国武汉举行.某电视台在19日至24日六天中共有7场直播(如下表所示),张三打算选取其中的三场观看.则观看的任意两场直播中间至少间隔一天(如第一场19日观看直播则20日不能观看直播)的概率是( )
日期
19日
20日
21日
22日
23日
24日
时间
全天
全天
上午
下午
全天
全天
全天
内容
飞行比赛
击剑
射击
游泳
篮球
定向越野
障碍跑
A.false B.false C.false D.false
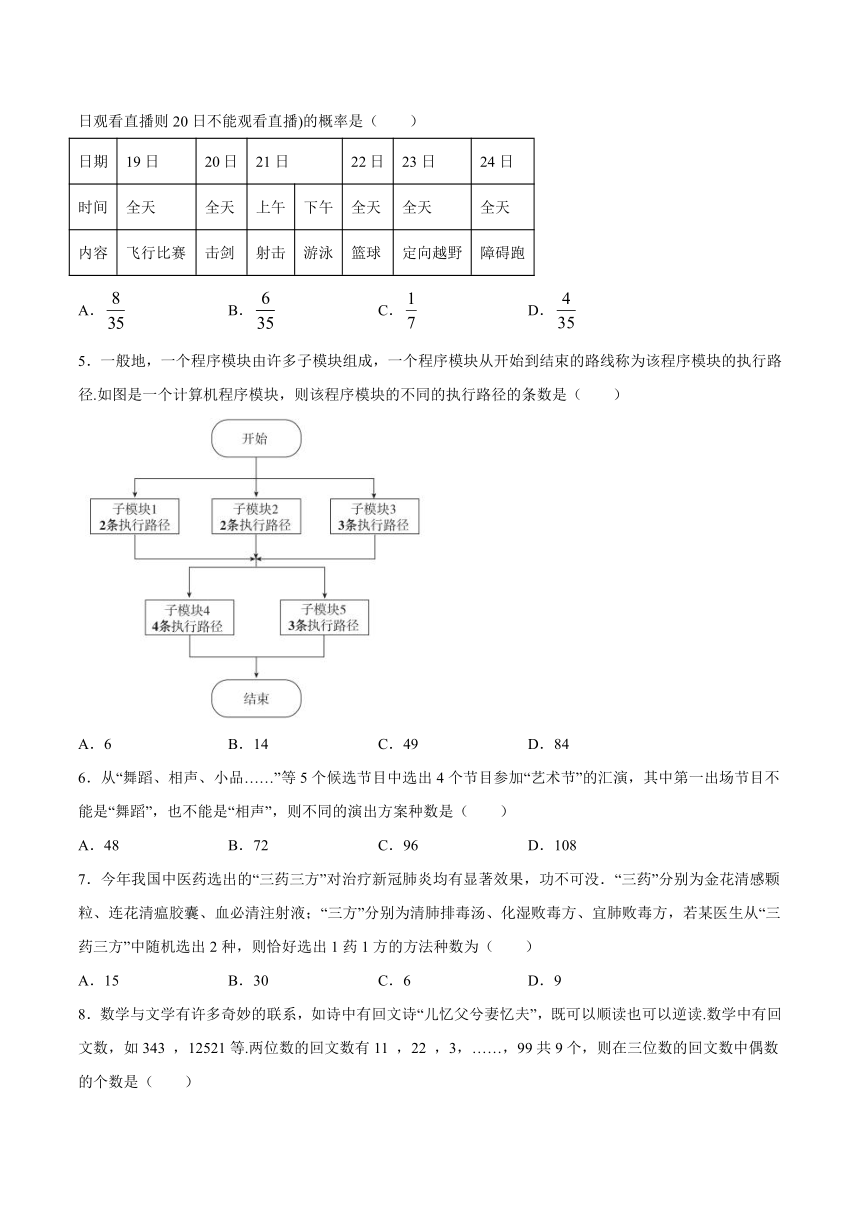
5.一般地,一个程序模块由许多子模块组成,一个程序模块从开始到结束的路线称为该程序模块的执行路径.如图是一个计算机程序模块,则该程序模块的不同的执行路径的条数是( )
A.6 B.14 C.49 D.84
6.从“舞蹈、相声、小品……”等5个候选节目中选出4个节目参加“艺术节”的汇演,其中第一出场节目不能是“舞蹈”,也不能是“相声”,则不同的演出方案种数是( )
A.48 B.72 C.96 D.108
7.今年我国中医药选出的“三药三方”对治疗新冠肺炎均有显著效果,功不可没.“三药”分别为金花清感颗粒、连花清瘟胶囊、血必清注射液;“三方”分别为清肺排毒汤、化湿败毒方、宜肺败毒方,若某医生从“三药三方”中随机选出2种,则恰好选出1药1方的方法种数为( )
A.15 B.30 C.6 D.9
8.数学与文学有许多奇妙的联系,如诗中有回文诗“儿忆父兮妻忆夫”,既可以顺读也可以逆读.数学中有回文数,如343 ,12521等.两位数的回文数有11 ,22 ,3,……,99共9个,则在三位数的回文数中偶数的个数是( )
A.40 B.30 C.20 D.10
9.若准备用1个字符给一本书编号,其中可用字符为字母false,false,false,也可用数字字符1,2,3,4,5,则不同的编号有( )
A.2种 B.5种 C.8种 D.15种
10.某景观湖内有四个人工小岛,为方便游客登岛观赏美景,现计划设计三座景观桥连通四个小岛,且每个小岛最多有两座桥连接,则设计方案的种数最多是( )
A.8 B.12 C.16 D.24
11.中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种.现有十二生肖的吉祥物各一个,已知甲同学喜欢牛、马和猴,乙同学喜欢牛、狗和羊,丙同学所有的吉祥物都喜欢,让甲乙丙三位同学依次从中选一个作为礼物珍藏,若各人所选取的礼物都是自己喜欢的,则不同的选法有( )
A.50种 B.60种 C.80种 D.90种
12.甲、乙、丙、丁四位同学计划去4个景点旅游,每人只去一个景点,设事件false=“四位同学去的景点不相同”,事件false=“甲同学独自去一个景点”,则false( )
A.false B.false C.false D.false
13.某校实行选科走班制度,张毅同学的选择是物理、生物、政治这三科,且物理在A层班级,生物在B层班级,该校周一上午课程安排如表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有( )
A.8种 B.10种 C.12种 D.14种
14.现有false位萌娃参加一项“寻宝贝,互助行”的游戏活动,宝贝的藏匿地点有远、近两处,其中亮亮的年龄比较小,要么不参与此项活动,但同时必须有另--位萌娃留下陪同;要么参与寻找近处的宝贝.所有参与寻找宝贝任务的萌娃被平均分成两组,一组去远处,一组去近处,那么不同的寻找方案有( )
A.false种 B.false种 C.false种 D.false种
15.某煤气站对外输送煤气时,用1至5号五个阀门控制,且必须遵守以下操作规则:
①若开启3号,则必须同时开启4号并且关闭2号;
②若开启2号或4号,则关闭1号;
③禁止同时关闭5号和1号.
则阀门的不同开闭方式种数为( )
A.7 B.8 C.11 D.14
16.要排出高三某班一天中,语文、数学、英语各false节,自习课false节的功课表,其中上午false节,下午false节,若要求false节语文课必须相邻且false节数学课也必须相邻(注意:上午第五节和下午第一节不算相邻),则不同的排法种数是( )
A.false B.false C.false D.false
17.“数独九宫格”原创者是18世纪的瑞士数学家欧拉,它的游戏规则很简单,将1到9这九个自然数填到如图所示的小九宫格的9个空格里,每个空格填一个数,且9个空格的数字各不相间,若中间空格已填数字5,且只填第二行和第二列,并要求第二行从左至右及第二列从上至下所填的数字都是从大到小排列的,则不同的填法种数为( )
A.72 B.108 C.144 D.196
18.一个国际象棋棋盘(由8×8个方格组成),其中有一个小方格因破损而被剪去(破损位置不确定).“L”形骨牌由三个相邻的小方格组成,如图所示.现要将这个破损的棋盘剪成数个“L”形骨牌,则( )
A.至多能剪成19块“L”形骨牌
B.至多能剪成20块“L”形骨牌
C.最多能剪成21块“L”形骨牌
D.前三个答案都不对
19.甲、乙、丙、丁和戊5名学生进行数学能力比赛,决出第一到第五名的名次(无并列名次).甲、乙两名同学去询问成绩,老师说:“虽然你们都没有得到第一,但你们也都不是最后一名”从上述回答分析,5人的名次不同的排列情况有( )
A.36种 B.48种 C.18种 D.54种
20.从集合{1,2,3,…,10}中任意选出三个不同的数,使这三个数成等比数列,这样的等比数列的个数为( )
A.3 B.4 C.6 D.8
第II卷(非选择题)
二、解答题
21.用0,1,…,9这十个数字可以组成多少个
(1)三位整数?
(2)无重复数字的三位整数?
(3)小于500的无重复数字的三位整数?
22.数学上的“四色问题”,是指“任何一张地图只用四种颜色就能使具有公共边界的国家着上不同的颜色.”,现有五种颜色供选择,涂色我国西部五省,要求每省涂一色,相邻各省不同色,有多少种涂色方法.
23.用5种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色,若要求相邻(有公共边)的区域不同色,则共有多少种不同的涂色方法?
1
2
3
4
24.用false这六个数字,完成下面两个小题.
(1)若数字不允许重复,可以组成多少个能被false整除的且百位数字不是false的不同的五位数;
(2)若直线方程false中的false可以从已知的六个数字中任取false个不同的数字,则直线方程表示的不同直线共有多少条?
25.有一项活动,需要在3名老师、8名男同学和5名女同学中选人参加.
(1)若只需选1人参加,则有多少种不同的选法?
(2)若需要老师、男同学、女同学各1人参加,则有多少种不同的选法?
(3)若需要1名老师、1名学生参加,则有多少种不同的选法?
参考答案
1.C
【分析】
由4位回文数只用排列前两位数字,后面数字随之确定,根据第一位不能为0,第二位任取,得到4位回文数的个数, 由第一位是奇数,第二位数任取,得到奇数的个数,代入古典概型的概率个数求解.
【详解】
4位回文数只用排列前两位数字,后面数字可以确定,
但是第一位不能为0,有9种情况,第二位有10种情况,
∴4位回文数有:false.
4位回文数的第一位是奇数,有5种情况,第二位有10种情况,
∴四位数的回文数中奇数的个数为:false,
∴在所有四位数的回文数中,出现奇数的概率为false.
故选:C.
2.D
【分析】
设每次分配一棵树种植的种植任务,分3步完成,按分步计数原理即可求解.
【详解】
解析:完成这件事需分三步.第1步,植第一棵树有4种不同的分配方法;
第2步,植第二棵树有4种不同的分配方法;
第3步,植第三棵树也有4种不同的分配方法.
由分步乘法计数原理得,共有不同的分配方法4×4×4=64(种).
故选:D
3.A
【分析】
利用分类加法计数原理,分别考虑false时的情况,由此分析出满足的有序自然数对的个数.
【详解】
解析: 当false时,false,有6个不同的有序自然数对;
当false时,false,有5个不同的有序自然数对;
当false时,false,有4个不同的有序自然数对;
根据分类加法计数原理可得,共有false个不同的有序自然数对,
故选:A.
4.B
【分析】
先求出false场直播中任意选取三场的种数,再计算选取的三场任意两场直播中间至少间隔一天的种数,利用概率除法公式即可求解.
【详解】
从false场直播中任意选取三场有false种,
三场任意两场直播中间至少间隔一天有四类:
选取false日,有false种,
选取false日,有false种,
选取false日,有1种,
选取false日,有1种,
所以选取的三场任意两场直播中间至少间隔一天的有false种,
所以概率为false,
故选:B
【点睛】
关键点点睛:本体的关键是准确求出false场直播中任意选取三场的种数,以及选取的三场任意两场直播中间至少间隔一天的种数,理解分类加法与分步乘法的区别.
5.C
【分析】
利用分类加法和分步乘法计数原理即可求解.
【详解】
由分类加法计数原理,子模块1或子模块2或子模块3的子路径共有false条;
子模块4或子模块5中的子路径共有false条,
由分步乘法计数原理,整个模块的不同执行路径共有false条,
故选:C
【点睛】
本题主要考查了分类加法计数原理和分步乘法计数原理,属于基础题.
6.B
【分析】
先在不是“舞蹈”和“相声”的三个节目中选一个安排在第一个出场有false种,再从剩下的四个节目中选三个节目依次演出有false,最后根据分步乘法计数原理得共有false种演出方案.
【详解】
第一步,先安排第一出场节目,第一出场节目不能是“舞蹈”也不能是“相声”则有false种选法;
第二步,在剩下的4个节目中选择3个节目并编排顺序,则有false种方法;
所以,共有false种演出方案.
故选:B.
【点睛】
本题考查排列问题,解题的关键在于分布完成问题,是基础题.
7.D
【分析】
根据题意,分析“1药”和“1方”的取法数目,由分步计数原理计算可得答案.
【详解】
解:根据题意,某医生从“三药三方”中随机选出2种,恰好选出1药1方,
则1药的取法有3种,1方的取法也有3种,
则恰好选出1药1方的方法种数为false;
故选:false.
【点睛】
本题考查排列组合的应用,涉及分类计数原理的应用,属于基础题.
8.A
【分析】
根据回文数定义,确定首位,再确定中间数,最后根据分步乘法计数原理得结果.
【详解】
由题意,若三位数的回文数是偶数,则末(首)位可能为false,false,false,false.如果末(首)位为false,
中间一位数有false种可能,同理可得,如果末(首)位为false或false或false,
中间一位数均有false种可能,所以有false个,
故选:A
【点睛】
本题考查分步计数原理实际应用,考查基本分析求解能力,属基础题.
9.C
【分析】
把编号所有可能情况分两类,一类字母,一类数字,两类数目相加可得.
【详解】
由题意这本书的编号可能是字母false,false,false,有3种
可能是数字:1,2,3,4,5,有效种,
共有3+5=8种.
故选:C.
【点睛】
本题考查分类计数原理,用列举法列出所有可能事件是常用方法.
10.B
【分析】
四个人工小岛记为ABCD,用“-”表示桥,对A分有一座桥相连和两座桥相连,一一列举,得到答案.
【详解】
四个人工小岛记为ABCD,对A分有一座桥相连和两座桥相连,用“-”表示桥
(1) A 只有一座桥相连时,有A-B-D-C,A-B-D-C,A-C-B-D,A-C-D-B,
A-D-B-C,A-D-C-B共6种;
(2) A有两座桥相连时,有C-A-B-D,D-A-B-C,D-A-C-B,B-A-C-D,
B-A-D-C,C-A-D-B共6种;
故共有12种.
故选:B
【点睛】
本题考查了分类计数原理的应用,考查了学生分析理解,逻辑推理的能力,属于中档题.
11.C
【分析】
根据题意,按甲的选择不同分成2种情况讨论,求出确定乙,丙的选择方法,即可得每种情况的选法数目,由分类加法计数原理,即可求出答案.
【详解】
解:根据题意,按甲的选择不同分成2种情况讨论:
若甲选择牛,此时乙的选择有2种,丙的选择有10种,
此时有false种不同的选法;
若甲选择马或猴,此时甲的选法有2种,乙的选择有3种,丙的选择有10种,
此时有false种不同的选法;
则一共有false种选法.
故选:C.
【点睛】
本题考查分步乘法和分类加法的计数原理的应用,属于基础题.
12.A
【分析】
由题意结合计数原理的知识求出所有基本事件数、false发生的基本事件数、false发生的基本事件数,由古典概型概率公式可得false、false,再利用条件概率概率公式即可得解.
【详解】
甲、乙、丙、丁四位同学计划去4个景点旅游,每人只去一个景点共有false个基本事件,
甲同学独自去一个景点,共有false个基本事件,则false;
事件false、false同时发生即事件false:四位同学去的景点不相同发生,共有false个基本事件,则false;
所以false.
故选:A.
【点睛】
本题考查了条件概率的求解,考查了计数原理与古典概型概率公式的应用,熟记公式、合理分步是解题关键,属于中档题.
13.B
【分析】
由课程表可知:物理课可以上任意一节,生物课只能上第2、3节,政治课只能上第1、3节,而自习课可以上任意一节.故以生物课(或政治课)进行分类,再分步排其他科目.由计数原理可得张毅同学不同的选课方法.
【详解】
由课程表可知:物理课可以上任意一节,生物课只能上第2、3节,政治课只能上第1、3、4节,而自习课可以上任意一节.
若生物课排第2节,则其他课可以任意排,共有false种不同的选课方法.
若生物课排第3节,则政治课有false种排法,其他课可以任意排,有false种排法,
共有false种不同的选课方法.
所以共有false种不同的选课方法.
故选:false.
【点睛】
本题考查两个计数原理,考查排列组合,属于基础题.
14.B
【分析】
按照亮亮参与,不参与游戏分类讨论,即可求出所有的寻找方案.
【详解】
(1)若亮亮不参与游戏,可以分三步完成萌娃的分配:①安排一位萌娃陪同亮亮,有5种选择:②从剩下的4个萌娃选择2个去近处,有false种选择;③最后剩下的2个去远处,完成分配,所以有false种方案.
(2)若亮亮参与游戏,可以分两步完成萌娃的分配:①从5个萌娃选择2个和亮亮去近处,有false种选择;②剩下的3个萌娃去远处,完成分配,所以有false种方案.
综上,不同的寻找方案有false种.
故选:B.
【点睛】
本题主要考查分步乘法计数原理和分类加法计数原理的应用,意在考查学生的知识应用能力,属于基础题.
15.A
【分析】
分两类解决,第一类:若开启3号,然后对2号和4号开启其中一个即可判断出1号和5号情况,第二类:若关闭3号,关闭2号关闭4号,对1号进行讨论,即可判断5号,由此可计算出结果.
【详解】
解:依题意,第一类:若开启3号,
则开启4号并且关闭2号,此时关闭1号,开启5号,
此时有1种方法;
第二类:若关闭3号,
①开启2号关闭4号或关闭2号开启4号或开启2号开启4号时,则关闭1号,开启5号,
此时有种3方法;
②关闭2号关闭4号,则开启1号关闭5号或开启1号开启5号或关闭1号,开启5号,
此时有种3方法;
综上所述,共有false种方式.
故选:A.
【点睛】
本题考查分类加法计数原理,属于中档题.
16.C
【分析】
根据题意,分两种情况进行讨论:①语文和数学都安排在上午;②语文和数学一个安排在上午,一个安排在下午.分别求出每一种情况的安排方法数目,由分类加法计数原理可得答案.
【详解】
根据题意,分两种情况进行讨论:
①语文和数学都安排在上午,要求false节语文课必须相邻且false节数学课也必须相邻,将false节语文课和false节数学课分别捆绑,然后在剩余false节课中选false节到上午,由于false节英语课不加以区分,此时,排法种数为false种;
②语文和数学都一个安排在上午,一个安排在下午.
语文和数学一个安排在上午,一个安排在下午,但false节语文课不加以区分,false节数学课不加以区分,false节英语课也不加以区分,此时,排法种数为false种.
综上所述,共有false种不同的排法.
故选:C.
【点睛】
本题考查排列、组合的应用,涉及分类计数原理的应用,属于中等题.
17.C
【分析】
分步完成,5的上方和左边只能从1,2,3,4中选取,5的下方和右边只能从6,7,8,9中选取.
【详解】
按题意5的上方和左边只能从1,2,3,4中选取,5的下方和右边只能从6,7,8,9中选取.因此填法总数为false.
故选:C.
【点睛】
本题考查分步计数原理.解题关键是确定完成这件事的方法.
18.C
【分析】
由2×3的6块方格10块和一个田字格组成棋盘,只要将破损的方格所在位置剪成一个恰当的田字格即可,所以最多能够剪成21块“L”形骨牌.
【详解】
考虑2×3的6块方格,如图:,每一块这样的骨牌含有2块“L”形骨牌
一共可以剪成10块这样的骨牌,和一个田字格,田字格可以剪1块“L”形骨牌,则一共21块“L”形骨牌.
只要将破损的方格所在位置剪成一个恰当的田字格即可,所以一定能够剪成21块“L”形骨牌.
如图所示
故选:C
【点睛】
此题考查根据图形特征结合计数原理求解,根据题目要求合理构造图形即可解题.
19.A
【分析】
利用分步计数原理直接求出名次的不同排列情况.
【详解】
解:甲和乙的限制最多,先排甲和乙有false种情况,
余下的3人有false种排法,所以共有false种排列情况.
故选:A.
【点睛】
本题考查了排列与简单的计数原理,解题的关键是弄清是分类还是分步完成,属基础题.
20.D
【分析】
直接利用枚举法写出所有的等比数列即可得到答案.
【详解】
(2)以1为首项的等比数列为1,2,4;1,3,9;
以2为首项的等比数列为2,4,8;
以4为首项的等比数列为4,6,9;
把这4个数列的顺序颠倒,又得到另外的4个数列,
∴所求的数列共有2(2+1+1)=8个.
故选:D.
【点睛】
本题考查了等比关系的确定,考查了学生观察问题的能力,是中档题.
21.(1)900个;(2)648个;(3)288个.
【分析】
(1)先考虑百位上数字,然后依次考虑十位和个数数字,用分步乘法原理.
(2)先考虑百位上数字,然后依次考虑十位和个数数字(注意不重复妈可),用分步乘法原理.
(3)首位有4种选择,十位和个位数字任意选择,由乘法原理可得.
【详解】
解:由于0不可在最高位,因此应对它进行单独考虑.
(1)百位的数字有9种选择,十位和个位的数字都各有10种选择,由分步乘法计数原理知,符合题意的三位数共有9×10×10=900(个).
(2)由于数字不可重复,可知百位的数字有9种选择,十位的数字也有9种选择,但个位数字仅有8种选择,由分步乘法计数原理知,符合题意的三位数共有9×9×8=648(个).
(3)百位只有4种选择,十位可有9种选择,个位数字有8种选择,由分步乘法计数原理知,符合题意的三位数共有4×9×8=288(个).
22.420种方法
【分析】
先涂新疆,再涂青海,再涂西藏,然后涂四川:分与新疆颜色相同和与新疆颜色不相同两类,则甘肃从剩下的和与西藏的颜色中选,最后利用分步、分类计数原理求解.
【详解】
对于新疆有5种涂色的方法,
对于青海有4种涂色方法,
对于西藏有3种涂色方法,
对于四川:若与新疆颜色相同,则有1种涂色方法,此时甘肃有3种涂色方法;
若四川与新疆颜色不相同,则四川只有2种涂色方法,此时甘肃有2种涂色方法;
根据分步、分类计数原理,则共有5×4×3×(2×2+1×3)=420种方法.
23.260
【分析】
利用分类加法计数原理把问题分成1号区域与4号区域同色,1号区域与4号区域不同色两种情况分析,每种情况用分步乘法计数原理求解,即可得出结果.
【详解】
解:第一类,1号区域与4号区域同色,此时可分三步来完成,
第一步,涂1号区域和4号区域,有5种涂法;
第二步,涂2号区域,只要不与1号区域和4号区域同色即可,因此有4种涂法;
第三步,涂3号区域,只要不与1号区域和4号区域同色即可,因此也有4种涂法.
由分步乘法计数原理知,有5×4×4=80种涂法.
第二类,1号区域与4号区域不同色,此时可分四步来完成,
第一步,涂1号区域,有5种涂法;
第二步,涂4号区域,只要不与1号区域同色即可,因此有4种涂法;
第三步,涂2号区域,只要不与1号区域和4号区域同色即可,因此有3种涂法;
第四步,涂3号区域,只要不与1号区域和4号区域同色即可,因此也有3种涂法.
由分步乘法计数原理知,有5×4×3×3=180种涂法.
依据分类加法计数原理知,不同涂色的方法种数为80+180=260.
24.(1)false(2)false
【详解】
(1)当末位数字是false时,百位数字有false个选择,共有false(个);
当末位数字是false,首位数字是false时,共有false个;
当末位数字是false时,首位数字是false或false或false时,共有false(个);
故共有false(个).
(2)false中有一个取false时,有false条;false都不取false时,有false(条);
false与false重复;false,与false重复.
故共有false(条).
考点:排列的应用,分类计数原理.
25.(1)16;(2)120;(3)39.
【分析】
(1)若只需选1人参加,用分类加法计数原理求出全部不同选法即可;
(2)用分步乘法计数原理,求出所有不同的选法;
(3)将男生女生归为一类,再用分步乘法计数原理求出所有不同选法即可.
【详解】
解:(1)需一人参加,有三类:第一类选老师,有3种不同的选法;第二类选男生,有8种不同的选法;第三类选女生,有5种不同的选法.共有false种不同的选法;
(2)需老师、男同学、女同学各一人,则分3步,第一步选老师,有3种不同的选法;第二步选男生,有8种不同的选法;第三步选女生,有5种不同的选法.共有false种不同的选法;
(3)第一步选老师有3种不同的选法,第二步选学生有false种不同的选法,共有false种不同的选法.
【点睛】
本题主要考查分类加法计数原理和分步乘法计数原理,考查运算求解能力,属于基础题型.
第I卷(选择题)
一、单选题
1.古希腊哲学家毕达哥拉斯曾说过:“美的线型和其他一切美的形体都必须有对称形式”.在中华传统文化里,建筑、器物、书法、诗歌、对联、绘画几乎无不讲究对称之美.如清代诗人黄柏权的《茶壶回文诗》(如图)以连环诗的形式展现,20个字绕着茶壶成一圆环,不论顺着读还是逆着读,皆成佳作.数学与生活也有许多奇妙的联系,如2020年02月02日(20200202)被称为世界完全对称日(公历纪年日期中数字左右完全对称的日期).数学上把20200202这样的对称数叫回文数,如两位数的回文数共有9个(11,22,…,99),则在所有四位数的回文数中,出现奇数的概率为( )
A.false B.false C.false D.false
2.植树节那天,有4名同学植树,现有3棵不同种类的树.若一棵树限1人完成,则不同的分配方法有( )
A.6种 B.3种
C.81种 D.64种
3.若false,且false,则满足条件的不同的有序自然数对false的个数是( )
A.15 B.12
C.5 D.4
4.第七届世界军运会于2019年10月18日至27日在中国武汉举行.某电视台在19日至24日六天中共有7场直播(如下表所示),张三打算选取其中的三场观看.则观看的任意两场直播中间至少间隔一天(如第一场19日观看直播则20日不能观看直播)的概率是( )
日期
19日
20日
21日
22日
23日
24日
时间
全天
全天
上午
下午
全天
全天
全天
内容
飞行比赛
击剑
射击
游泳
篮球
定向越野
障碍跑
A.false B.false C.false D.false
5.一般地,一个程序模块由许多子模块组成,一个程序模块从开始到结束的路线称为该程序模块的执行路径.如图是一个计算机程序模块,则该程序模块的不同的执行路径的条数是( )
A.6 B.14 C.49 D.84
6.从“舞蹈、相声、小品……”等5个候选节目中选出4个节目参加“艺术节”的汇演,其中第一出场节目不能是“舞蹈”,也不能是“相声”,则不同的演出方案种数是( )
A.48 B.72 C.96 D.108
7.今年我国中医药选出的“三药三方”对治疗新冠肺炎均有显著效果,功不可没.“三药”分别为金花清感颗粒、连花清瘟胶囊、血必清注射液;“三方”分别为清肺排毒汤、化湿败毒方、宜肺败毒方,若某医生从“三药三方”中随机选出2种,则恰好选出1药1方的方法种数为( )
A.15 B.30 C.6 D.9
8.数学与文学有许多奇妙的联系,如诗中有回文诗“儿忆父兮妻忆夫”,既可以顺读也可以逆读.数学中有回文数,如343 ,12521等.两位数的回文数有11 ,22 ,3,……,99共9个,则在三位数的回文数中偶数的个数是( )
A.40 B.30 C.20 D.10
9.若准备用1个字符给一本书编号,其中可用字符为字母false,false,false,也可用数字字符1,2,3,4,5,则不同的编号有( )
A.2种 B.5种 C.8种 D.15种
10.某景观湖内有四个人工小岛,为方便游客登岛观赏美景,现计划设计三座景观桥连通四个小岛,且每个小岛最多有两座桥连接,则设计方案的种数最多是( )
A.8 B.12 C.16 D.24
11.中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种.现有十二生肖的吉祥物各一个,已知甲同学喜欢牛、马和猴,乙同学喜欢牛、狗和羊,丙同学所有的吉祥物都喜欢,让甲乙丙三位同学依次从中选一个作为礼物珍藏,若各人所选取的礼物都是自己喜欢的,则不同的选法有( )
A.50种 B.60种 C.80种 D.90种
12.甲、乙、丙、丁四位同学计划去4个景点旅游,每人只去一个景点,设事件false=“四位同学去的景点不相同”,事件false=“甲同学独自去一个景点”,则false( )
A.false B.false C.false D.false
13.某校实行选科走班制度,张毅同学的选择是物理、生物、政治这三科,且物理在A层班级,生物在B层班级,该校周一上午课程安排如表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有( )
A.8种 B.10种 C.12种 D.14种
14.现有false位萌娃参加一项“寻宝贝,互助行”的游戏活动,宝贝的藏匿地点有远、近两处,其中亮亮的年龄比较小,要么不参与此项活动,但同时必须有另--位萌娃留下陪同;要么参与寻找近处的宝贝.所有参与寻找宝贝任务的萌娃被平均分成两组,一组去远处,一组去近处,那么不同的寻找方案有( )
A.false种 B.false种 C.false种 D.false种
15.某煤气站对外输送煤气时,用1至5号五个阀门控制,且必须遵守以下操作规则:
①若开启3号,则必须同时开启4号并且关闭2号;
②若开启2号或4号,则关闭1号;
③禁止同时关闭5号和1号.
则阀门的不同开闭方式种数为( )
A.7 B.8 C.11 D.14
16.要排出高三某班一天中,语文、数学、英语各false节,自习课false节的功课表,其中上午false节,下午false节,若要求false节语文课必须相邻且false节数学课也必须相邻(注意:上午第五节和下午第一节不算相邻),则不同的排法种数是( )
A.false B.false C.false D.false
17.“数独九宫格”原创者是18世纪的瑞士数学家欧拉,它的游戏规则很简单,将1到9这九个自然数填到如图所示的小九宫格的9个空格里,每个空格填一个数,且9个空格的数字各不相间,若中间空格已填数字5,且只填第二行和第二列,并要求第二行从左至右及第二列从上至下所填的数字都是从大到小排列的,则不同的填法种数为( )
A.72 B.108 C.144 D.196
18.一个国际象棋棋盘(由8×8个方格组成),其中有一个小方格因破损而被剪去(破损位置不确定).“L”形骨牌由三个相邻的小方格组成,如图所示.现要将这个破损的棋盘剪成数个“L”形骨牌,则( )
A.至多能剪成19块“L”形骨牌
B.至多能剪成20块“L”形骨牌
C.最多能剪成21块“L”形骨牌
D.前三个答案都不对
19.甲、乙、丙、丁和戊5名学生进行数学能力比赛,决出第一到第五名的名次(无并列名次).甲、乙两名同学去询问成绩,老师说:“虽然你们都没有得到第一,但你们也都不是最后一名”从上述回答分析,5人的名次不同的排列情况有( )
A.36种 B.48种 C.18种 D.54种
20.从集合{1,2,3,…,10}中任意选出三个不同的数,使这三个数成等比数列,这样的等比数列的个数为( )
A.3 B.4 C.6 D.8
第II卷(非选择题)
二、解答题
21.用0,1,…,9这十个数字可以组成多少个
(1)三位整数?
(2)无重复数字的三位整数?
(3)小于500的无重复数字的三位整数?
22.数学上的“四色问题”,是指“任何一张地图只用四种颜色就能使具有公共边界的国家着上不同的颜色.”,现有五种颜色供选择,涂色我国西部五省,要求每省涂一色,相邻各省不同色,有多少种涂色方法.
23.用5种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色,若要求相邻(有公共边)的区域不同色,则共有多少种不同的涂色方法?
1
2
3
4
24.用false这六个数字,完成下面两个小题.
(1)若数字不允许重复,可以组成多少个能被false整除的且百位数字不是false的不同的五位数;
(2)若直线方程false中的false可以从已知的六个数字中任取false个不同的数字,则直线方程表示的不同直线共有多少条?
25.有一项活动,需要在3名老师、8名男同学和5名女同学中选人参加.
(1)若只需选1人参加,则有多少种不同的选法?
(2)若需要老师、男同学、女同学各1人参加,则有多少种不同的选法?
(3)若需要1名老师、1名学生参加,则有多少种不同的选法?
参考答案
1.C
【分析】
由4位回文数只用排列前两位数字,后面数字随之确定,根据第一位不能为0,第二位任取,得到4位回文数的个数, 由第一位是奇数,第二位数任取,得到奇数的个数,代入古典概型的概率个数求解.
【详解】
4位回文数只用排列前两位数字,后面数字可以确定,
但是第一位不能为0,有9种情况,第二位有10种情况,
∴4位回文数有:false.
4位回文数的第一位是奇数,有5种情况,第二位有10种情况,
∴四位数的回文数中奇数的个数为:false,
∴在所有四位数的回文数中,出现奇数的概率为false.
故选:C.
2.D
【分析】
设每次分配一棵树种植的种植任务,分3步完成,按分步计数原理即可求解.
【详解】
解析:完成这件事需分三步.第1步,植第一棵树有4种不同的分配方法;
第2步,植第二棵树有4种不同的分配方法;
第3步,植第三棵树也有4种不同的分配方法.
由分步乘法计数原理得,共有不同的分配方法4×4×4=64(种).
故选:D
3.A
【分析】
利用分类加法计数原理,分别考虑false时的情况,由此分析出满足的有序自然数对的个数.
【详解】
解析: 当false时,false,有6个不同的有序自然数对;
当false时,false,有5个不同的有序自然数对;
当false时,false,有4个不同的有序自然数对;
根据分类加法计数原理可得,共有false个不同的有序自然数对,
故选:A.
4.B
【分析】
先求出false场直播中任意选取三场的种数,再计算选取的三场任意两场直播中间至少间隔一天的种数,利用概率除法公式即可求解.
【详解】
从false场直播中任意选取三场有false种,
三场任意两场直播中间至少间隔一天有四类:
选取false日,有false种,
选取false日,有false种,
选取false日,有1种,
选取false日,有1种,
所以选取的三场任意两场直播中间至少间隔一天的有false种,
所以概率为false,
故选:B
【点睛】
关键点点睛:本体的关键是准确求出false场直播中任意选取三场的种数,以及选取的三场任意两场直播中间至少间隔一天的种数,理解分类加法与分步乘法的区别.
5.C
【分析】
利用分类加法和分步乘法计数原理即可求解.
【详解】
由分类加法计数原理,子模块1或子模块2或子模块3的子路径共有false条;
子模块4或子模块5中的子路径共有false条,
由分步乘法计数原理,整个模块的不同执行路径共有false条,
故选:C
【点睛】
本题主要考查了分类加法计数原理和分步乘法计数原理,属于基础题.
6.B
【分析】
先在不是“舞蹈”和“相声”的三个节目中选一个安排在第一个出场有false种,再从剩下的四个节目中选三个节目依次演出有false,最后根据分步乘法计数原理得共有false种演出方案.
【详解】
第一步,先安排第一出场节目,第一出场节目不能是“舞蹈”也不能是“相声”则有false种选法;
第二步,在剩下的4个节目中选择3个节目并编排顺序,则有false种方法;
所以,共有false种演出方案.
故选:B.
【点睛】
本题考查排列问题,解题的关键在于分布完成问题,是基础题.
7.D
【分析】
根据题意,分析“1药”和“1方”的取法数目,由分步计数原理计算可得答案.
【详解】
解:根据题意,某医生从“三药三方”中随机选出2种,恰好选出1药1方,
则1药的取法有3种,1方的取法也有3种,
则恰好选出1药1方的方法种数为false;
故选:false.
【点睛】
本题考查排列组合的应用,涉及分类计数原理的应用,属于基础题.
8.A
【分析】
根据回文数定义,确定首位,再确定中间数,最后根据分步乘法计数原理得结果.
【详解】
由题意,若三位数的回文数是偶数,则末(首)位可能为false,false,false,false.如果末(首)位为false,
中间一位数有false种可能,同理可得,如果末(首)位为false或false或false,
中间一位数均有false种可能,所以有false个,
故选:A
【点睛】
本题考查分步计数原理实际应用,考查基本分析求解能力,属基础题.
9.C
【分析】
把编号所有可能情况分两类,一类字母,一类数字,两类数目相加可得.
【详解】
由题意这本书的编号可能是字母false,false,false,有3种
可能是数字:1,2,3,4,5,有效种,
共有3+5=8种.
故选:C.
【点睛】
本题考查分类计数原理,用列举法列出所有可能事件是常用方法.
10.B
【分析】
四个人工小岛记为ABCD,用“-”表示桥,对A分有一座桥相连和两座桥相连,一一列举,得到答案.
【详解】
四个人工小岛记为ABCD,对A分有一座桥相连和两座桥相连,用“-”表示桥
(1) A 只有一座桥相连时,有A-B-D-C,A-B-D-C,A-C-B-D,A-C-D-B,
A-D-B-C,A-D-C-B共6种;
(2) A有两座桥相连时,有C-A-B-D,D-A-B-C,D-A-C-B,B-A-C-D,
B-A-D-C,C-A-D-B共6种;
故共有12种.
故选:B
【点睛】
本题考查了分类计数原理的应用,考查了学生分析理解,逻辑推理的能力,属于中档题.
11.C
【分析】
根据题意,按甲的选择不同分成2种情况讨论,求出确定乙,丙的选择方法,即可得每种情况的选法数目,由分类加法计数原理,即可求出答案.
【详解】
解:根据题意,按甲的选择不同分成2种情况讨论:
若甲选择牛,此时乙的选择有2种,丙的选择有10种,
此时有false种不同的选法;
若甲选择马或猴,此时甲的选法有2种,乙的选择有3种,丙的选择有10种,
此时有false种不同的选法;
则一共有false种选法.
故选:C.
【点睛】
本题考查分步乘法和分类加法的计数原理的应用,属于基础题.
12.A
【分析】
由题意结合计数原理的知识求出所有基本事件数、false发生的基本事件数、false发生的基本事件数,由古典概型概率公式可得false、false,再利用条件概率概率公式即可得解.
【详解】
甲、乙、丙、丁四位同学计划去4个景点旅游,每人只去一个景点共有false个基本事件,
甲同学独自去一个景点,共有false个基本事件,则false;
事件false、false同时发生即事件false:四位同学去的景点不相同发生,共有false个基本事件,则false;
所以false.
故选:A.
【点睛】
本题考查了条件概率的求解,考查了计数原理与古典概型概率公式的应用,熟记公式、合理分步是解题关键,属于中档题.
13.B
【分析】
由课程表可知:物理课可以上任意一节,生物课只能上第2、3节,政治课只能上第1、3节,而自习课可以上任意一节.故以生物课(或政治课)进行分类,再分步排其他科目.由计数原理可得张毅同学不同的选课方法.
【详解】
由课程表可知:物理课可以上任意一节,生物课只能上第2、3节,政治课只能上第1、3、4节,而自习课可以上任意一节.
若生物课排第2节,则其他课可以任意排,共有false种不同的选课方法.
若生物课排第3节,则政治课有false种排法,其他课可以任意排,有false种排法,
共有false种不同的选课方法.
所以共有false种不同的选课方法.
故选:false.
【点睛】
本题考查两个计数原理,考查排列组合,属于基础题.
14.B
【分析】
按照亮亮参与,不参与游戏分类讨论,即可求出所有的寻找方案.
【详解】
(1)若亮亮不参与游戏,可以分三步完成萌娃的分配:①安排一位萌娃陪同亮亮,有5种选择:②从剩下的4个萌娃选择2个去近处,有false种选择;③最后剩下的2个去远处,完成分配,所以有false种方案.
(2)若亮亮参与游戏,可以分两步完成萌娃的分配:①从5个萌娃选择2个和亮亮去近处,有false种选择;②剩下的3个萌娃去远处,完成分配,所以有false种方案.
综上,不同的寻找方案有false种.
故选:B.
【点睛】
本题主要考查分步乘法计数原理和分类加法计数原理的应用,意在考查学生的知识应用能力,属于基础题.
15.A
【分析】
分两类解决,第一类:若开启3号,然后对2号和4号开启其中一个即可判断出1号和5号情况,第二类:若关闭3号,关闭2号关闭4号,对1号进行讨论,即可判断5号,由此可计算出结果.
【详解】
解:依题意,第一类:若开启3号,
则开启4号并且关闭2号,此时关闭1号,开启5号,
此时有1种方法;
第二类:若关闭3号,
①开启2号关闭4号或关闭2号开启4号或开启2号开启4号时,则关闭1号,开启5号,
此时有种3方法;
②关闭2号关闭4号,则开启1号关闭5号或开启1号开启5号或关闭1号,开启5号,
此时有种3方法;
综上所述,共有false种方式.
故选:A.
【点睛】
本题考查分类加法计数原理,属于中档题.
16.C
【分析】
根据题意,分两种情况进行讨论:①语文和数学都安排在上午;②语文和数学一个安排在上午,一个安排在下午.分别求出每一种情况的安排方法数目,由分类加法计数原理可得答案.
【详解】
根据题意,分两种情况进行讨论:
①语文和数学都安排在上午,要求false节语文课必须相邻且false节数学课也必须相邻,将false节语文课和false节数学课分别捆绑,然后在剩余false节课中选false节到上午,由于false节英语课不加以区分,此时,排法种数为false种;
②语文和数学都一个安排在上午,一个安排在下午.
语文和数学一个安排在上午,一个安排在下午,但false节语文课不加以区分,false节数学课不加以区分,false节英语课也不加以区分,此时,排法种数为false种.
综上所述,共有false种不同的排法.
故选:C.
【点睛】
本题考查排列、组合的应用,涉及分类计数原理的应用,属于中等题.
17.C
【分析】
分步完成,5的上方和左边只能从1,2,3,4中选取,5的下方和右边只能从6,7,8,9中选取.
【详解】
按题意5的上方和左边只能从1,2,3,4中选取,5的下方和右边只能从6,7,8,9中选取.因此填法总数为false.
故选:C.
【点睛】
本题考查分步计数原理.解题关键是确定完成这件事的方法.
18.C
【分析】
由2×3的6块方格10块和一个田字格组成棋盘,只要将破损的方格所在位置剪成一个恰当的田字格即可,所以最多能够剪成21块“L”形骨牌.
【详解】
考虑2×3的6块方格,如图:,每一块这样的骨牌含有2块“L”形骨牌
一共可以剪成10块这样的骨牌,和一个田字格,田字格可以剪1块“L”形骨牌,则一共21块“L”形骨牌.
只要将破损的方格所在位置剪成一个恰当的田字格即可,所以一定能够剪成21块“L”形骨牌.
如图所示
故选:C
【点睛】
此题考查根据图形特征结合计数原理求解,根据题目要求合理构造图形即可解题.
19.A
【分析】
利用分步计数原理直接求出名次的不同排列情况.
【详解】
解:甲和乙的限制最多,先排甲和乙有false种情况,
余下的3人有false种排法,所以共有false种排列情况.
故选:A.
【点睛】
本题考查了排列与简单的计数原理,解题的关键是弄清是分类还是分步完成,属基础题.
20.D
【分析】
直接利用枚举法写出所有的等比数列即可得到答案.
【详解】
(2)以1为首项的等比数列为1,2,4;1,3,9;
以2为首项的等比数列为2,4,8;
以4为首项的等比数列为4,6,9;
把这4个数列的顺序颠倒,又得到另外的4个数列,
∴所求的数列共有2(2+1+1)=8个.
故选:D.
【点睛】
本题考查了等比关系的确定,考查了学生观察问题的能力,是中档题.
21.(1)900个;(2)648个;(3)288个.
【分析】
(1)先考虑百位上数字,然后依次考虑十位和个数数字,用分步乘法原理.
(2)先考虑百位上数字,然后依次考虑十位和个数数字(注意不重复妈可),用分步乘法原理.
(3)首位有4种选择,十位和个位数字任意选择,由乘法原理可得.
【详解】
解:由于0不可在最高位,因此应对它进行单独考虑.
(1)百位的数字有9种选择,十位和个位的数字都各有10种选择,由分步乘法计数原理知,符合题意的三位数共有9×10×10=900(个).
(2)由于数字不可重复,可知百位的数字有9种选择,十位的数字也有9种选择,但个位数字仅有8种选择,由分步乘法计数原理知,符合题意的三位数共有9×9×8=648(个).
(3)百位只有4种选择,十位可有9种选择,个位数字有8种选择,由分步乘法计数原理知,符合题意的三位数共有4×9×8=288(个).
22.420种方法
【分析】
先涂新疆,再涂青海,再涂西藏,然后涂四川:分与新疆颜色相同和与新疆颜色不相同两类,则甘肃从剩下的和与西藏的颜色中选,最后利用分步、分类计数原理求解.
【详解】
对于新疆有5种涂色的方法,
对于青海有4种涂色方法,
对于西藏有3种涂色方法,
对于四川:若与新疆颜色相同,则有1种涂色方法,此时甘肃有3种涂色方法;
若四川与新疆颜色不相同,则四川只有2种涂色方法,此时甘肃有2种涂色方法;
根据分步、分类计数原理,则共有5×4×3×(2×2+1×3)=420种方法.
23.260
【分析】
利用分类加法计数原理把问题分成1号区域与4号区域同色,1号区域与4号区域不同色两种情况分析,每种情况用分步乘法计数原理求解,即可得出结果.
【详解】
解:第一类,1号区域与4号区域同色,此时可分三步来完成,
第一步,涂1号区域和4号区域,有5种涂法;
第二步,涂2号区域,只要不与1号区域和4号区域同色即可,因此有4种涂法;
第三步,涂3号区域,只要不与1号区域和4号区域同色即可,因此也有4种涂法.
由分步乘法计数原理知,有5×4×4=80种涂法.
第二类,1号区域与4号区域不同色,此时可分四步来完成,
第一步,涂1号区域,有5种涂法;
第二步,涂4号区域,只要不与1号区域同色即可,因此有4种涂法;
第三步,涂2号区域,只要不与1号区域和4号区域同色即可,因此有3种涂法;
第四步,涂3号区域,只要不与1号区域和4号区域同色即可,因此也有3种涂法.
由分步乘法计数原理知,有5×4×3×3=180种涂法.
依据分类加法计数原理知,不同涂色的方法种数为80+180=260.
24.(1)false(2)false
【详解】
(1)当末位数字是false时,百位数字有false个选择,共有false(个);
当末位数字是false,首位数字是false时,共有false个;
当末位数字是false时,首位数字是false或false或false时,共有false(个);
故共有false(个).
(2)false中有一个取false时,有false条;false都不取false时,有false(条);
false与false重复;false,与false重复.
故共有false(条).
考点:排列的应用,分类计数原理.
25.(1)16;(2)120;(3)39.
【分析】
(1)若只需选1人参加,用分类加法计数原理求出全部不同选法即可;
(2)用分步乘法计数原理,求出所有不同的选法;
(3)将男生女生归为一类,再用分步乘法计数原理求出所有不同选法即可.
【详解】
解:(1)需一人参加,有三类:第一类选老师,有3种不同的选法;第二类选男生,有8种不同的选法;第三类选女生,有5种不同的选法.共有false种不同的选法;
(2)需老师、男同学、女同学各一人,则分3步,第一步选老师,有3种不同的选法;第二步选男生,有8种不同的选法;第三步选女生,有5种不同的选法.共有false种不同的选法;
(3)第一步选老师有3种不同的选法,第二步选学生有false种不同的选法,共有false种不同的选法.
【点睛】
本题主要考查分类加法计数原理和分步乘法计数原理,考查运算求解能力,属于基础题型.
