7.4二项分布与超几何分布-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册练习(含答案)
文档属性
| 名称 | 7.4二项分布与超几何分布-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 659.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 09:36:54 | ||
图片预览




文档简介
7.4二项分布与超几何分布
第I卷(选择题)
一、单选题
1.如表所示是采取一项单独防疫措施感染COVID-19的概率统计表:
单独防疫措施
戴口罩
勤洗手
接种COVID-19疫苗
感染COVID-19的概率
false
false
false
一次核酸检测的准确率为false.某家有3人,他们每个人只戴口罩,没有做到勤洗手也没有接种COVID-19疫苗,感染COVID-19的概率都为0.01.这3人不同人的核酸检测结果,以及其中任何一个人的不同次核酸检测结果都是互相独立的.他们3人都落实了表中的三项防疫措施,而且共做了10次核酸检测.以这家人的每个人每次核酸检测被确诊感染COVID-19的概率为依据,这10次核酸检测中,有false次结果为确诊,false的数学期望为( )
A.false B.false C.false D.false
2.口袋里放有大小相同的两个红球和一个白球,每次有放回地摸取一个球,定义数列{an},当第false次摸取到的是红球时,false;当第false次摸取到的是白球时,false,如果Sn为数列{an}的前n项和,那么S7=3的概率为( )
A.false B.false
C.false D.false
3.某人从家乘车到单位,途中经过3个路口.假设在各路口遇到红灯的事件是相互独立的,且概率都是0.4,则此人上班途中遇到红灯的次数的方差为( )
A.0.48 B.1.2
C.0.72 D.0.6
4.抛掷一枚质地均匀的正方体骰子4次,设false表示向上一面出现6点的次数,则false的数学期望false的值为( )
A.false B.false C.false D.false
5.袋中有3个白球和i个黑球,有放回的摸取3次,每次摸取一球,设摸得黑球的个数为false,其中false,则( )
A.false,false B.false,false
C.false,false D.false,false
6.纹样是中国传统文化的重要组成部分,它既代表着中华民族的悠久历史、社会的发展进步,也是世界文化艺术宝库中的巨大财富.小楠从小就对纹样艺术有浓厚的兴趣.收集了如下9枚纹样微章,其中4枚凤纹徽章,5枚龙纹微章.小楠从9枚徽章中任取3枚,则其中至少有一枚凤纹徽章的概率为( ).
A.false B.false C.false D.false
7.某市某校在秋季运动会中,安排了篮球投篮比赛.现有20名同学参加篮球投篮比赛,已知每名同学投进的概率均为0.4,每名同学有2次投篮机会,且各同学投篮之间没有影响.现规定:投进两个得4分,投进一个得2分,一个未进得0分,则其中一名同学得2分的概率为
A.0.5 B.0.48 C.0.4 D.0.32
8.现有一条零件生产线,每个零件达到优等品的概率都为false.某检验员从该生产线上随机抽检false个零件,设其中优等品零件的个数为false.若false,falsefalse,则false
A.false B.false C.false D.false
9.从一批含有13件正品、2件次品的产品中,不放回地任取3件,则取出产品中无次品的概率为( )
A.false B.false C.false D.false
10.若随机变量false,且false,则false的值是( )
A.false B.false C.false D.false
11.已知随机变量X服从二项分布false.若false,false,则false( )
A.false B.false C.false D.false
12.已知false,则false、false的值依次为( ).
A.3,2 B.2,3 C.6,2 D.2,6
13.若X~B(20,0.3),则( )
A.E(X)=3 B.P(X≥1)=1﹣0.320
C.D(X)=4 D.P(X=10)false
14.设随机变量false,false,若false,则false( )
A.false B.false C.false D.false
15.某篮球运动员每次投篮投中的概率是false,每次投篮的结果相互独立,那么在他10次投篮中,记最有可能投中的次数为false,则false的值为( )
A.5 B.6 C.7 D.8
16.唐代诗人张若虚在《春江花月夜》中曾写道:“春江潮水连海平,海上明月共潮生.”潮水的涨落和月亮的公转运行有直接的关系,这是一种自然现象.根据历史数据,已知沿海某地在某个季节中每天出现大潮的概率均为false,则该地在该季节内连续三天内,至少有两天出现大潮的概率为( )
A.false B.false C.false D.false
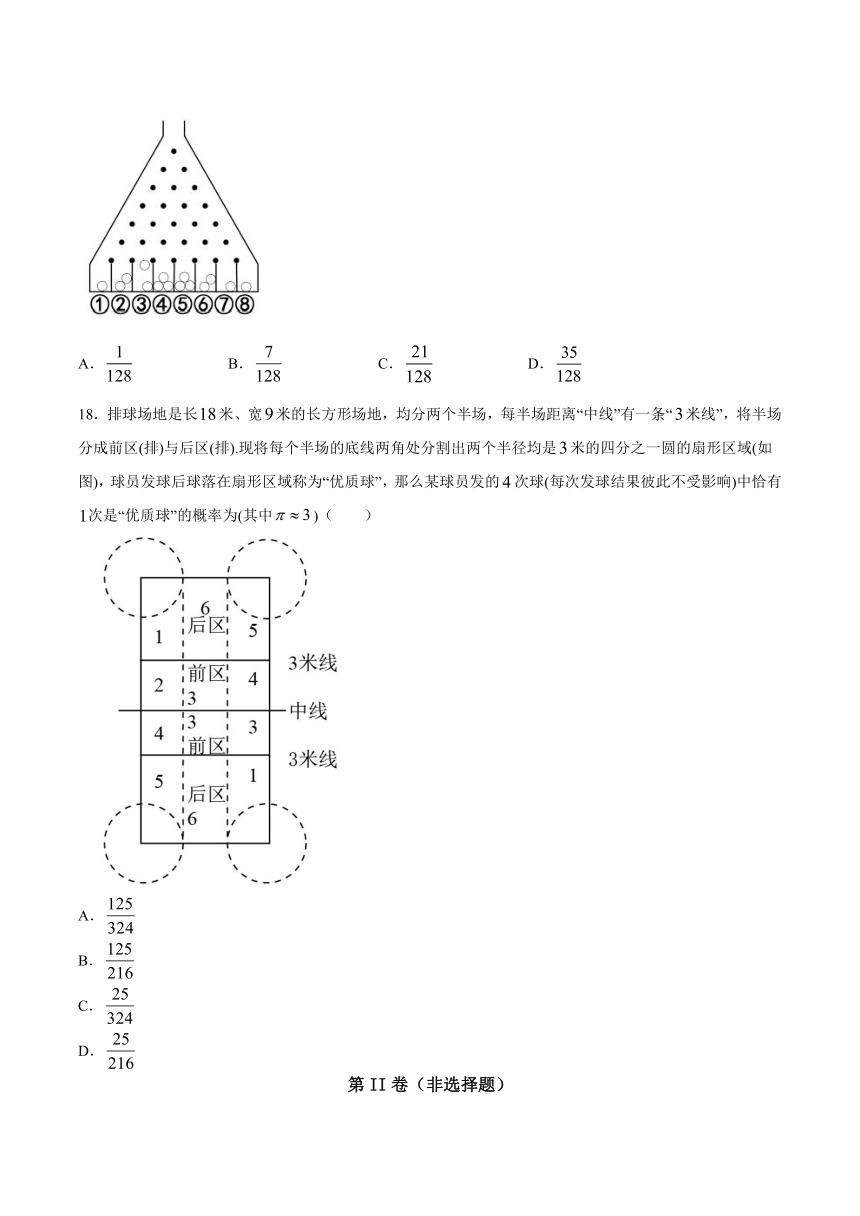
17.2020年12月4日,中国科学技术大学宣布该校潘建伟等科学家成功构建false光子的量子计算原型机“九章”,求解数学算法“高斯玻色取样”只需要false秒,而目前世界最快的超级计算机要用false亿年,这一突破使我国成为全球第二个实现“量子优越性”的国家.“九章”求得的问题名叫“高斯玻色取样”,通俗的可以理解为量子版本的高尔顿钉板,但其实际情况非常复杂.高尔顿钉板是英国生物学家高尔顿设计的,如图,每一个黑点表示钉在板上的一颗钉子,上一层的每个钉子水平位置恰好位于下一层的两颗钉子的正中间,从入口处放进一个直径略小于两颗钉子之间距离的白色圆玻璃球,白球向下降落的过程中,首先碰到最上面的钉子,碰到钉子后皆以二分之一的概率向左或向右滚下,于是又碰到下一层钉子.如此继续下去,直到滚到底板的一个格子内为止.现从入口放进一个白球,则其落在第③个格子的概率为
A.false B.false C.false D.false
18.排球场地是长false米、宽false米的长方形场地,均分两个半场,每半场距离“中线”有一条“false米线”,将半场分成前区(排)与后区(排).现将每个半场的底线两角处分割出两个半径均是false米的四分之一圆的扇形区域(如图),球员发球后球落在扇形区域称为“优质球”,那么某球员发的false次球(每次发球结果彼此不受影响)中恰有false次是“优质球”的概率为(其中false)( )
A.false
B.false
C.false
D.false
第II卷(非选择题)
二、解答题
19.微信语音正成为手机一族重要的联系方式,为了解某市微信语音的使用情况,某公司随机抽查了100名微信语音用户,得到如下数据:
每天使用微信语音次数
1
2
3
4
5
6及以上
30岁及以下人数
3
3
4
7
8
30
30岁以上人数
4
5
6
4
6
20
合计
7
8
10
11
14
50
(1)如果认为每天使用超过3次微信语音的用户是“喜欢使用微信语音”,完成下面false列联表,并判断能否在犯错误概率不超过0.05的前提下,认为“喜欢使用微信语音”与年龄有关?
不喜欢使用微信语音
喜欢使用微信语音
合计
30岁及以下人数
30岁以上人数
合计
(2)每天使用6次及以上微信语音的人称为“微信语音达人”,视频率为概率,在该市所有“微信语音达人”中随机抽取3名用户.
①抽取的3名用户,既有30岁及以下的“微信语音达人”又有30岁以上“微信语音达人”的概率;
②为鼓励30岁以上用户使用微信语音,对抽取的30岁以上“微信语音达人”,每人奖励100元话费,记奖励总金额为false,求false的数学期望.
附:false,其中false.
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
20.某公司开发了一款手机应用软件,为了解用户对这款软件的满意度,推出该软件3个月后,从使用该软件的用户中随机抽查了1000名,将所得的满意度的分数分成7组:false,整理得到如下频率分布直方图.根据所得的满意度的分数,将用户的满意度分为两个等级:
满意度的分数
false
false
满意度的等级
不满意
满意
(1)从使用该软件的用户中随机抽取1人,估计其满意度的等级为“满意”的概率;
(2)用频率估计概率,从使用该软件的所有用户中随机抽取2人,以X表示这2人中满意度的等级为“满意”的人数,求X的分布列和数学期望.
21.师大附中学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)记录了他们的幸福度分数.
(1)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”,求从这16人中随机选取3人,至多有1人的幸福度是“极幸福”的概率;
(2)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记ξ表示选到幸福度为“极幸福”的人数,求false的分布列及数学期望.
22.某研发公司研制出一款保护视力的护眼仪,并在某中学的甲、乙、丙、丁四个班级中试用,这四个班级人数的条形图如图所示,为了了解学生对护眼仪的使用情况,对四个班级的学生进行了问卷调查,然后按分层抽样的方法从调查问卷中抽取false份进行统计,统计结果如表所示.
甲班
乙班
丙班
丁班
满意
50%
80%
100%
60%
一般
25%
0
0
0
不满意
25%
20%
0
40%
(1)若学生A在甲班,求学生A的调查问卷被选中的概率;
(2)以这false人的样本数据来估计整个学校的总体数据,若从该校false人数很多false任选false人,设false表示抽到“满意”学生的人数,求false的分布列及数学期望.
23.为提升销量,某电商在其网店首页设置了一个“勇闯关,贏红包”的游戏小程序,其游戏规则如下:在网页上设置三个翻牌关卡,每个关卡翻牌结果只有两种:Pass(通过)与Fail(失败),若买家通过这三关,则认为闯关成功;若三关均未通过或只通过三关中的一关,则游戏失败;若三关中恰好通过两关,则允许参加复活环节.复活环节有两个翻牌关卡,若两关均通过,也认为闯关成功,否则认为闯关失败.假定买家每一关通过的概率均为false,且各关卡之间是否通过相互独立.
(1)求某买家参加这个游戏闯关成功的概率;
(2)若闯关成功,则买家可赢得50元的购物红包.若闯关失败.则可获得10元红包,红包均可直抵在该网店购物的货款.某日有8100人参与了游戏且均在该网店消费.
(ⅰ)求该日所有买家所获红包总金额false的数学期望:
(ⅱ)假定该电商能从未中奖的买家的购物中平均获利8元/人,从中奖的买家的购物中平均获利120元/人(均不含所发红包在内).试从数学期望的角度判断该电商这一日通过游戏搞促销活动是否合算,并说明理由.
参考答案
1.B
【分析】
题意说明false,然后由相互独立事件的概率公式计算出落实三项措施后感染的概率,结合准确率可得此人核酸检测一次确诊的概率为false,则false,然后由二项分布的期望计算出期望.
【详解】
根据条件,false.一个人落实了表中三项防疫措施后,感染COVID-19的概率为false,一次核酸检测的准确率为false,这个人再进行一次核酸检测,可知此人被核酸检测确诊感染COVID-19的概率为falsefalse.以这家人核酸检测确诊感染COVID-19的概率为依据,这家3人10次核酸检测中被确诊感染COVID-19的次数为false,
∴false.
故选:B.
2.B
【分析】
根据S7=3知7次摸球中摸取红球和白球的次数,结合古典概型概率求出每次摸球时摸到红球的概率和摸到白球的概率,从而可选出正确答案.
【详解】
解析:由S7=3知,在7次摸球中有2次摸取红球,5次摸取白球,每次摸红球的概率为false,摸取白球的概率为false,则S7=3的概率为false,
故选:B.
3.C
【分析】
设此人上班途中遇到红灯的次数为X,则X~B(3,0.4),由二项分布方差公式计算可得.
【详解】
设此人上班途中遇到红灯的次数为X,则X~B(3,0.4),
所以D(X)=3×0.4×0.6=0.72.
故选:C.
4.D
【分析】
先确定抛掷一枚质地均匀的正方体骰子1次,向上一面出现6点的概率,再根据二项分布数学期望公式求得结果.
【详解】
抛掷一枚质地均匀的正方体骰子1次,向上一面出现6点的概率为false
false
故选:D
5.A
【分析】
由题意得,当false时,false可能的取值为:false,可得falsefalse,当false时,false可能的取值为:false,可得falsefalse,由二项分布分布列求得其相应的期望和方差,比较大小可得选项.
【详解】
当false时,false可能的取值为:false,则:
false,false,false,false,
所以falsefalse,所以false,false;
当false时,false可能的取值为:false,则:
false,false,false,false,
所以falsefalse,所以false,false;
所以false,false,
故选:A.
6.B
【分析】
本题首先可以确定所有可能事件的数量为false,然后确定满足“一枚凤纹徽章也没有”的所有可能事件的数目为false,最后根据“至少有一枚凤纹徽章”的对立事件为“一枚凤纹徽章也没有”即可得出结果.
【详解】
从9枚纹样微章中选择3枚,所有可能事件的数量为false,
满足“一枚凤纹徽章也没有”的所有可能事件的数目为false,
因为“至少有一枚凤纹徽章”的对立事件为“一枚凤纹徽章也没有”,
所以false,
故选:B.
7.B
【分析】
事件“第一次投进球”和“第二次投进球”是相互独立的,利用对立事件和相互独立事件可求“其中一名同学得2分”的概率.
【详解】
设“第一次投进球”为事件false,“第二次投进球”为事件false,则得2分的概率为falsefalse.故选B.
8.C
【分析】
由false求出的范围,再由方差公式求出值.
【详解】
∵false,∴false,化简得false,即false,又false,解得false或false,∴false,故选C.
9.A
【分析】
先求得产品总数,然后利用超几何分布概率计算公式计算出所求的概率.
【详解】
依题意可知,产品总数为false件,由超几何分布概率计算公式得取出产品中无次品的概率为false,故选A.
10.C
【详解】
试题分析:根据随机变量符合二项分布,根据期望值求出n的值,写出对应的自变量的概率的计算公式,代入自变量等于1时的值.
解:∵E(X)=3,
∴0.6n=3,
∴n=5
∴P(X=1)=C51(0.6)1(0.4)4=3×0.44
故选C.
考点:二项分布与n次独立重复试验的模型.
11.C
【分析】
由随机变量X服从二项分布B(n,p),结合期望及方差的公式运算即可得解.
【详解】
由随机变量X服从二项分布B(n,p).
又E(X)=2, false,
所以np=2,np(1?p)= false,
解得:p=false,
故选:C.
12.A
【分析】
直接利用二项分布公式计算得到答案.
【详解】
false,则false,false
故选:false
13.D
【分析】
根据二项分布的均值,方差以及概率公式求解即可.
【详解】
因为false,所以false,false
false
false
故选:D
14.A
【分析】
先建立方程false求出false,再计算false即可.
【详解】
解:因为随机变量false,false,
所以false,则false,
因为false,即false,解得false
随机变量false中,
false,
故选:A
15.D
【分析】
先记投篮命中的次数为随机变量false,根据题意,得到false服从二项分布,求出false取最大时false的值,即可得出结果.
【详解】
记投篮命中的次数为随机变量false,
由题意,false,
则投篮命中false次的概率为false,
由false得false,即false,即false,
解得false,又false,
因此false时,false取最大值.
即该运动员10次投篮中,最有可能投中的次数为false次.
故选:D.
16.A
【分析】
利用二项分布的概率公式以及概率的加法公式即可求解.
【详解】
该地在该季节内连续三天内,至少有两天出现大潮包括两天或三天出现大潮,
有两天出现大潮概率为false,
有三天出现大潮概率为false,
所以至少有两天出现大潮的概率为false,
故选:A.
17.C
【分析】
小球从起点到第③个格子一共跳了7次,其中要向右边跳动2次,由二项分布概率即可求解.
【详解】
小球从起点到第③个格子一共跳了7次,其中要向左边跳动5次,向右边跳动2次,而向左或向右的概率均为false,则向右的次数服从二项分布,所以所求的概率为false
故答案为:C.
18.A
【分析】
根据几何概型的概率计算公式求出是“优质球”的概率,再利用二项分布的概率计算公式即可求解.
【详解】
由已知,两个四分之一圆的扇形区域的面积为falsefalse,
而半个场地的面积为falsefalse,
由几何概型的概率计算公式得发一次球是“优质球”的概率为false,
从而发的false次球中恰有false次是“优质球”的概率false,
故选:A.
19.(1)列联表见解析,见解析;(2)①false;②120.
【分析】
(1)先补充完整false列联表,再由参考公式计算false的观测值false,并与附表对照,即可得出结论;
(2)①该市“微信语音达人”有50人,30岁及以下的有30人,30岁以上的20人,再由组合数和古典概型,得解;
②记抽出的30岁以上“微信语音达人”的人数为false,根据二项分布知识可得结果.
【详解】
(1)由题中表格数据可得false列联表如下:
不喜欢使用微信语音
喜欢使用微信语音
合计
30岁及以下人数
10
45
55
30岁以上人数
15
30
45
合计
25
75
100
将列表中的数据代入公式计算得:
false的观测值false,
所以在犯错误率不超过0.05的前提下,不能认为是否“喜欢使用微信语音”与年龄有关.
(2)视频率为概率,该市“微信语音达人”有50人,30岁及以下的有30人,30岁以上的20人.随机抽取1名用户,该用户为30岁及以下的“微信语音达人”的概率为false,该用户为30岁以上的“微信语音达人”的概率为false.
①抽收的3名用户中,既有30岁及以下“微信语音达人”又有30岁以上“微信语音达人”的概率为false.
②记抽出的30岁以上“微信语音达人”的人数为false,则false.
由题意得false,∴false,
所以false的数学期望false.
20.(1)false;(2)分布列见解析,期望为false;
【分析】
(1)根据频率分布直方图求出在false与false的频率,即可得到概率;
(2)依题意false,则false的可能取值为false、false、false,求出所对应的概率,列出分布列,求出数学期望即可;
【详解】
解:(1)由频率分布直方图可知满意度的分数false的频率为false,满意度的分数false的频率为false,故从使用该软件的用户中随机抽取1人,其满意度的等级为“满意”的概率为false
(2)依题意可知false,则false的可能取值为false、false、false,
所以false,false,false
所以false的分布列为:
false
false
false
false
false
false
false
false
所以false
21.(1)false ;(2)分布列见解析;期望为false.
【分析】
(1)设false表示所取false人中有false个人是“极幸福”,至多有false人是“极幸福”记为事件false,根据题中条件,利用古典概型的概率计算公式,即可求出结果.
(2)false的可能取值为false,false,false,false,分析题意可知false服从二项分布,求出对应的概率,即可求得其分布列及其期望.
【详解】
(1)设false表示所取false人中有false个人是“极幸福”,至多有false人是“极幸福”记为事件false,
则由茎叶图可得:false;
(2)由题意,false的可能取值为false,false,false,false,
从该社区任选一人,幸福度为“极幸福”的概率为false,
所以false,
则false,false,false,false,
则false的分布列为:
false
false
false
false
false
false
false
false
false
false
∴期望为false.
22.(1)0.1;(2)分布列见解析,3.
【分析】
(1)由条形图可知四个班的总数,由分层抽样可求得甲班问卷中的份数,从而可求出概率;
(2)由图可知调查的false人中满意人数占比为false,由题意得false,人而可求出false的分布列及数学期望.
【详解】
(1)由条形图可得,甲、乙、丙、丁四个班共有false人,其中甲班人数为false人,
由分层抽样可得从甲班问卷中抽取了false份,所以学生A的调查问卷被选中的概率是false.
(2)由图可知,甲、乙、丙、丁四个班接受调查的人数分别为false,false,false,false,其中满意人数分别为false,false,false,false,
即调查的false人中满意人数占比为false.
由题意得false,故false.
false的分布列为:
false
0
1
2
3
4
false
false
false
false
false
false
所以false.
23.(1)false;(2)(ⅰ)101000元;(ⅱ)合算,理由见解析.
【分析】
(1)分买家通过三关和买家参加复活环节并闯关成功分别求出概率并求和.
(2)(ⅰ)由(1)可知,一名买家闯关成功的概率false,则false,而false,可求出答案.
(ii) 设电商该日剔除红包款后盈利false元,则false,可得出答案.
【详解】
解:(1)买家通过三关的概率为false,
买家参加复活环节并闯关成功的概率为false,
所以买家闯关成功的概率false.
(2)(ⅰ)由(1)可知,一名买家闯关成功的概率false,
设这8100名买家中闯关成功的人数为false,
则false,
且false,
所以false的数学期望为false,
所以该日所有买家所获红包总金额false的数学期望为
false元.
(ⅱ)设电商该日剔除红包款后盈利false元,
则false元,
由此可见,该电商该日通过游戏搞促销活动盈利较多,很合算.
第I卷(选择题)
一、单选题
1.如表所示是采取一项单独防疫措施感染COVID-19的概率统计表:
单独防疫措施
戴口罩
勤洗手
接种COVID-19疫苗
感染COVID-19的概率
false
false
false
一次核酸检测的准确率为false.某家有3人,他们每个人只戴口罩,没有做到勤洗手也没有接种COVID-19疫苗,感染COVID-19的概率都为0.01.这3人不同人的核酸检测结果,以及其中任何一个人的不同次核酸检测结果都是互相独立的.他们3人都落实了表中的三项防疫措施,而且共做了10次核酸检测.以这家人的每个人每次核酸检测被确诊感染COVID-19的概率为依据,这10次核酸检测中,有false次结果为确诊,false的数学期望为( )
A.false B.false C.false D.false
2.口袋里放有大小相同的两个红球和一个白球,每次有放回地摸取一个球,定义数列{an},当第false次摸取到的是红球时,false;当第false次摸取到的是白球时,false,如果Sn为数列{an}的前n项和,那么S7=3的概率为( )
A.false B.false
C.false D.false
3.某人从家乘车到单位,途中经过3个路口.假设在各路口遇到红灯的事件是相互独立的,且概率都是0.4,则此人上班途中遇到红灯的次数的方差为( )
A.0.48 B.1.2
C.0.72 D.0.6
4.抛掷一枚质地均匀的正方体骰子4次,设false表示向上一面出现6点的次数,则false的数学期望false的值为( )
A.false B.false C.false D.false
5.袋中有3个白球和i个黑球,有放回的摸取3次,每次摸取一球,设摸得黑球的个数为false,其中false,则( )
A.false,false B.false,false
C.false,false D.false,false
6.纹样是中国传统文化的重要组成部分,它既代表着中华民族的悠久历史、社会的发展进步,也是世界文化艺术宝库中的巨大财富.小楠从小就对纹样艺术有浓厚的兴趣.收集了如下9枚纹样微章,其中4枚凤纹徽章,5枚龙纹微章.小楠从9枚徽章中任取3枚,则其中至少有一枚凤纹徽章的概率为( ).
A.false B.false C.false D.false
7.某市某校在秋季运动会中,安排了篮球投篮比赛.现有20名同学参加篮球投篮比赛,已知每名同学投进的概率均为0.4,每名同学有2次投篮机会,且各同学投篮之间没有影响.现规定:投进两个得4分,投进一个得2分,一个未进得0分,则其中一名同学得2分的概率为
A.0.5 B.0.48 C.0.4 D.0.32
8.现有一条零件生产线,每个零件达到优等品的概率都为false.某检验员从该生产线上随机抽检false个零件,设其中优等品零件的个数为false.若false,falsefalse,则false
A.false B.false C.false D.false
9.从一批含有13件正品、2件次品的产品中,不放回地任取3件,则取出产品中无次品的概率为( )
A.false B.false C.false D.false
10.若随机变量false,且false,则false的值是( )
A.false B.false C.false D.false
11.已知随机变量X服从二项分布false.若false,false,则false( )
A.false B.false C.false D.false
12.已知false,则false、false的值依次为( ).
A.3,2 B.2,3 C.6,2 D.2,6
13.若X~B(20,0.3),则( )
A.E(X)=3 B.P(X≥1)=1﹣0.320
C.D(X)=4 D.P(X=10)false
14.设随机变量false,false,若false,则false( )
A.false B.false C.false D.false
15.某篮球运动员每次投篮投中的概率是false,每次投篮的结果相互独立,那么在他10次投篮中,记最有可能投中的次数为false,则false的值为( )
A.5 B.6 C.7 D.8
16.唐代诗人张若虚在《春江花月夜》中曾写道:“春江潮水连海平,海上明月共潮生.”潮水的涨落和月亮的公转运行有直接的关系,这是一种自然现象.根据历史数据,已知沿海某地在某个季节中每天出现大潮的概率均为false,则该地在该季节内连续三天内,至少有两天出现大潮的概率为( )
A.false B.false C.false D.false
17.2020年12月4日,中国科学技术大学宣布该校潘建伟等科学家成功构建false光子的量子计算原型机“九章”,求解数学算法“高斯玻色取样”只需要false秒,而目前世界最快的超级计算机要用false亿年,这一突破使我国成为全球第二个实现“量子优越性”的国家.“九章”求得的问题名叫“高斯玻色取样”,通俗的可以理解为量子版本的高尔顿钉板,但其实际情况非常复杂.高尔顿钉板是英国生物学家高尔顿设计的,如图,每一个黑点表示钉在板上的一颗钉子,上一层的每个钉子水平位置恰好位于下一层的两颗钉子的正中间,从入口处放进一个直径略小于两颗钉子之间距离的白色圆玻璃球,白球向下降落的过程中,首先碰到最上面的钉子,碰到钉子后皆以二分之一的概率向左或向右滚下,于是又碰到下一层钉子.如此继续下去,直到滚到底板的一个格子内为止.现从入口放进一个白球,则其落在第③个格子的概率为
A.false B.false C.false D.false
18.排球场地是长false米、宽false米的长方形场地,均分两个半场,每半场距离“中线”有一条“false米线”,将半场分成前区(排)与后区(排).现将每个半场的底线两角处分割出两个半径均是false米的四分之一圆的扇形区域(如图),球员发球后球落在扇形区域称为“优质球”,那么某球员发的false次球(每次发球结果彼此不受影响)中恰有false次是“优质球”的概率为(其中false)( )
A.false
B.false
C.false
D.false
第II卷(非选择题)
二、解答题
19.微信语音正成为手机一族重要的联系方式,为了解某市微信语音的使用情况,某公司随机抽查了100名微信语音用户,得到如下数据:
每天使用微信语音次数
1
2
3
4
5
6及以上
30岁及以下人数
3
3
4
7
8
30
30岁以上人数
4
5
6
4
6
20
合计
7
8
10
11
14
50
(1)如果认为每天使用超过3次微信语音的用户是“喜欢使用微信语音”,完成下面false列联表,并判断能否在犯错误概率不超过0.05的前提下,认为“喜欢使用微信语音”与年龄有关?
不喜欢使用微信语音
喜欢使用微信语音
合计
30岁及以下人数
30岁以上人数
合计
(2)每天使用6次及以上微信语音的人称为“微信语音达人”,视频率为概率,在该市所有“微信语音达人”中随机抽取3名用户.
①抽取的3名用户,既有30岁及以下的“微信语音达人”又有30岁以上“微信语音达人”的概率;
②为鼓励30岁以上用户使用微信语音,对抽取的30岁以上“微信语音达人”,每人奖励100元话费,记奖励总金额为false,求false的数学期望.
附:false,其中false.
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
20.某公司开发了一款手机应用软件,为了解用户对这款软件的满意度,推出该软件3个月后,从使用该软件的用户中随机抽查了1000名,将所得的满意度的分数分成7组:false,整理得到如下频率分布直方图.根据所得的满意度的分数,将用户的满意度分为两个等级:
满意度的分数
false
false
满意度的等级
不满意
满意
(1)从使用该软件的用户中随机抽取1人,估计其满意度的等级为“满意”的概率;
(2)用频率估计概率,从使用该软件的所有用户中随机抽取2人,以X表示这2人中满意度的等级为“满意”的人数,求X的分布列和数学期望.
21.师大附中学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)记录了他们的幸福度分数.
(1)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”,求从这16人中随机选取3人,至多有1人的幸福度是“极幸福”的概率;
(2)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记ξ表示选到幸福度为“极幸福”的人数,求false的分布列及数学期望.
22.某研发公司研制出一款保护视力的护眼仪,并在某中学的甲、乙、丙、丁四个班级中试用,这四个班级人数的条形图如图所示,为了了解学生对护眼仪的使用情况,对四个班级的学生进行了问卷调查,然后按分层抽样的方法从调查问卷中抽取false份进行统计,统计结果如表所示.
甲班
乙班
丙班
丁班
满意
50%
80%
100%
60%
一般
25%
0
0
0
不满意
25%
20%
0
40%
(1)若学生A在甲班,求学生A的调查问卷被选中的概率;
(2)以这false人的样本数据来估计整个学校的总体数据,若从该校false人数很多false任选false人,设false表示抽到“满意”学生的人数,求false的分布列及数学期望.
23.为提升销量,某电商在其网店首页设置了一个“勇闯关,贏红包”的游戏小程序,其游戏规则如下:在网页上设置三个翻牌关卡,每个关卡翻牌结果只有两种:Pass(通过)与Fail(失败),若买家通过这三关,则认为闯关成功;若三关均未通过或只通过三关中的一关,则游戏失败;若三关中恰好通过两关,则允许参加复活环节.复活环节有两个翻牌关卡,若两关均通过,也认为闯关成功,否则认为闯关失败.假定买家每一关通过的概率均为false,且各关卡之间是否通过相互独立.
(1)求某买家参加这个游戏闯关成功的概率;
(2)若闯关成功,则买家可赢得50元的购物红包.若闯关失败.则可获得10元红包,红包均可直抵在该网店购物的货款.某日有8100人参与了游戏且均在该网店消费.
(ⅰ)求该日所有买家所获红包总金额false的数学期望:
(ⅱ)假定该电商能从未中奖的买家的购物中平均获利8元/人,从中奖的买家的购物中平均获利120元/人(均不含所发红包在内).试从数学期望的角度判断该电商这一日通过游戏搞促销活动是否合算,并说明理由.
参考答案
1.B
【分析】
题意说明false,然后由相互独立事件的概率公式计算出落实三项措施后感染的概率,结合准确率可得此人核酸检测一次确诊的概率为false,则false,然后由二项分布的期望计算出期望.
【详解】
根据条件,false.一个人落实了表中三项防疫措施后,感染COVID-19的概率为false,一次核酸检测的准确率为false,这个人再进行一次核酸检测,可知此人被核酸检测确诊感染COVID-19的概率为falsefalse.以这家人核酸检测确诊感染COVID-19的概率为依据,这家3人10次核酸检测中被确诊感染COVID-19的次数为false,
∴false.
故选:B.
2.B
【分析】
根据S7=3知7次摸球中摸取红球和白球的次数,结合古典概型概率求出每次摸球时摸到红球的概率和摸到白球的概率,从而可选出正确答案.
【详解】
解析:由S7=3知,在7次摸球中有2次摸取红球,5次摸取白球,每次摸红球的概率为false,摸取白球的概率为false,则S7=3的概率为false,
故选:B.
3.C
【分析】
设此人上班途中遇到红灯的次数为X,则X~B(3,0.4),由二项分布方差公式计算可得.
【详解】
设此人上班途中遇到红灯的次数为X,则X~B(3,0.4),
所以D(X)=3×0.4×0.6=0.72.
故选:C.
4.D
【分析】
先确定抛掷一枚质地均匀的正方体骰子1次,向上一面出现6点的概率,再根据二项分布数学期望公式求得结果.
【详解】
抛掷一枚质地均匀的正方体骰子1次,向上一面出现6点的概率为false
false
故选:D
5.A
【分析】
由题意得,当false时,false可能的取值为:false,可得falsefalse,当false时,false可能的取值为:false,可得falsefalse,由二项分布分布列求得其相应的期望和方差,比较大小可得选项.
【详解】
当false时,false可能的取值为:false,则:
false,false,false,false,
所以falsefalse,所以false,false;
当false时,false可能的取值为:false,则:
false,false,false,false,
所以falsefalse,所以false,false;
所以false,false,
故选:A.
6.B
【分析】
本题首先可以确定所有可能事件的数量为false,然后确定满足“一枚凤纹徽章也没有”的所有可能事件的数目为false,最后根据“至少有一枚凤纹徽章”的对立事件为“一枚凤纹徽章也没有”即可得出结果.
【详解】
从9枚纹样微章中选择3枚,所有可能事件的数量为false,
满足“一枚凤纹徽章也没有”的所有可能事件的数目为false,
因为“至少有一枚凤纹徽章”的对立事件为“一枚凤纹徽章也没有”,
所以false,
故选:B.
7.B
【分析】
事件“第一次投进球”和“第二次投进球”是相互独立的,利用对立事件和相互独立事件可求“其中一名同学得2分”的概率.
【详解】
设“第一次投进球”为事件false,“第二次投进球”为事件false,则得2分的概率为falsefalse.故选B.
8.C
【分析】
由false求出的范围,再由方差公式求出值.
【详解】
∵false,∴false,化简得false,即false,又false,解得false或false,∴false,故选C.
9.A
【分析】
先求得产品总数,然后利用超几何分布概率计算公式计算出所求的概率.
【详解】
依题意可知,产品总数为false件,由超几何分布概率计算公式得取出产品中无次品的概率为false,故选A.
10.C
【详解】
试题分析:根据随机变量符合二项分布,根据期望值求出n的值,写出对应的自变量的概率的计算公式,代入自变量等于1时的值.
解:∵E(X)=3,
∴0.6n=3,
∴n=5
∴P(X=1)=C51(0.6)1(0.4)4=3×0.44
故选C.
考点:二项分布与n次独立重复试验的模型.
11.C
【分析】
由随机变量X服从二项分布B(n,p),结合期望及方差的公式运算即可得解.
【详解】
由随机变量X服从二项分布B(n,p).
又E(X)=2, false,
所以np=2,np(1?p)= false,
解得:p=false,
故选:C.
12.A
【分析】
直接利用二项分布公式计算得到答案.
【详解】
false,则false,false
故选:false
13.D
【分析】
根据二项分布的均值,方差以及概率公式求解即可.
【详解】
因为false,所以false,false
false
false
故选:D
14.A
【分析】
先建立方程false求出false,再计算false即可.
【详解】
解:因为随机变量false,false,
所以false,则false,
因为false,即false,解得false
随机变量false中,
false,
故选:A
15.D
【分析】
先记投篮命中的次数为随机变量false,根据题意,得到false服从二项分布,求出false取最大时false的值,即可得出结果.
【详解】
记投篮命中的次数为随机变量false,
由题意,false,
则投篮命中false次的概率为false,
由false得false,即false,即false,
解得false,又false,
因此false时,false取最大值.
即该运动员10次投篮中,最有可能投中的次数为false次.
故选:D.
16.A
【分析】
利用二项分布的概率公式以及概率的加法公式即可求解.
【详解】
该地在该季节内连续三天内,至少有两天出现大潮包括两天或三天出现大潮,
有两天出现大潮概率为false,
有三天出现大潮概率为false,
所以至少有两天出现大潮的概率为false,
故选:A.
17.C
【分析】
小球从起点到第③个格子一共跳了7次,其中要向右边跳动2次,由二项分布概率即可求解.
【详解】
小球从起点到第③个格子一共跳了7次,其中要向左边跳动5次,向右边跳动2次,而向左或向右的概率均为false,则向右的次数服从二项分布,所以所求的概率为false
故答案为:C.
18.A
【分析】
根据几何概型的概率计算公式求出是“优质球”的概率,再利用二项分布的概率计算公式即可求解.
【详解】
由已知,两个四分之一圆的扇形区域的面积为falsefalse,
而半个场地的面积为falsefalse,
由几何概型的概率计算公式得发一次球是“优质球”的概率为false,
从而发的false次球中恰有false次是“优质球”的概率false,
故选:A.
19.(1)列联表见解析,见解析;(2)①false;②120.
【分析】
(1)先补充完整false列联表,再由参考公式计算false的观测值false,并与附表对照,即可得出结论;
(2)①该市“微信语音达人”有50人,30岁及以下的有30人,30岁以上的20人,再由组合数和古典概型,得解;
②记抽出的30岁以上“微信语音达人”的人数为false,根据二项分布知识可得结果.
【详解】
(1)由题中表格数据可得false列联表如下:
不喜欢使用微信语音
喜欢使用微信语音
合计
30岁及以下人数
10
45
55
30岁以上人数
15
30
45
合计
25
75
100
将列表中的数据代入公式计算得:
false的观测值false,
所以在犯错误率不超过0.05的前提下,不能认为是否“喜欢使用微信语音”与年龄有关.
(2)视频率为概率,该市“微信语音达人”有50人,30岁及以下的有30人,30岁以上的20人.随机抽取1名用户,该用户为30岁及以下的“微信语音达人”的概率为false,该用户为30岁以上的“微信语音达人”的概率为false.
①抽收的3名用户中,既有30岁及以下“微信语音达人”又有30岁以上“微信语音达人”的概率为false.
②记抽出的30岁以上“微信语音达人”的人数为false,则false.
由题意得false,∴false,
所以false的数学期望false.
20.(1)false;(2)分布列见解析,期望为false;
【分析】
(1)根据频率分布直方图求出在false与false的频率,即可得到概率;
(2)依题意false,则false的可能取值为false、false、false,求出所对应的概率,列出分布列,求出数学期望即可;
【详解】
解:(1)由频率分布直方图可知满意度的分数false的频率为false,满意度的分数false的频率为false,故从使用该软件的用户中随机抽取1人,其满意度的等级为“满意”的概率为false
(2)依题意可知false,则false的可能取值为false、false、false,
所以false,false,false
所以false的分布列为:
false
false
false
false
false
false
false
false
所以false
21.(1)false ;(2)分布列见解析;期望为false.
【分析】
(1)设false表示所取false人中有false个人是“极幸福”,至多有false人是“极幸福”记为事件false,根据题中条件,利用古典概型的概率计算公式,即可求出结果.
(2)false的可能取值为false,false,false,false,分析题意可知false服从二项分布,求出对应的概率,即可求得其分布列及其期望.
【详解】
(1)设false表示所取false人中有false个人是“极幸福”,至多有false人是“极幸福”记为事件false,
则由茎叶图可得:false;
(2)由题意,false的可能取值为false,false,false,false,
从该社区任选一人,幸福度为“极幸福”的概率为false,
所以false,
则false,false,false,false,
则false的分布列为:
false
false
false
false
false
false
false
false
false
false
∴期望为false.
22.(1)0.1;(2)分布列见解析,3.
【分析】
(1)由条形图可知四个班的总数,由分层抽样可求得甲班问卷中的份数,从而可求出概率;
(2)由图可知调查的false人中满意人数占比为false,由题意得false,人而可求出false的分布列及数学期望.
【详解】
(1)由条形图可得,甲、乙、丙、丁四个班共有false人,其中甲班人数为false人,
由分层抽样可得从甲班问卷中抽取了false份,所以学生A的调查问卷被选中的概率是false.
(2)由图可知,甲、乙、丙、丁四个班接受调查的人数分别为false,false,false,false,其中满意人数分别为false,false,false,false,
即调查的false人中满意人数占比为false.
由题意得false,故false.
false的分布列为:
false
0
1
2
3
4
false
false
false
false
false
false
所以false.
23.(1)false;(2)(ⅰ)101000元;(ⅱ)合算,理由见解析.
【分析】
(1)分买家通过三关和买家参加复活环节并闯关成功分别求出概率并求和.
(2)(ⅰ)由(1)可知,一名买家闯关成功的概率false,则false,而false,可求出答案.
(ii) 设电商该日剔除红包款后盈利false元,则false,可得出答案.
【详解】
解:(1)买家通过三关的概率为false,
买家参加复活环节并闯关成功的概率为false,
所以买家闯关成功的概率false.
(2)(ⅰ)由(1)可知,一名买家闯关成功的概率false,
设这8100名买家中闯关成功的人数为false,
则false,
且false,
所以false的数学期望为false,
所以该日所有买家所获红包总金额false的数学期望为
false元.
(ⅱ)设电商该日剔除红包款后盈利false元,
则false元,
由此可见,该电商该日通过游戏搞促销活动盈利较多,很合算.
