2.3.1向量的数乘运算-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(27张PPT)
文档属性
| 名称 | 2.3.1向量的数乘运算-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 921.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 00:00:00 | ||
图片预览






文档简介
向量的数乘运算
授课教师:
温故知新
学习目标
1.理解数乘向量的概念及其几何意义;(重点)
2.掌握数乘向量的运算律,能进行简单运算.(难
点)
课文精讲
在疾风骤雨、雷电交加的夜晚,为什么我
们总是先看到闪电,后听到雷声?这是因为光
速远远大于声速.经测量,光速大小约为声速
的8.8×105倍.
数乘运算的定义
课文精讲
一重物由高空自由落下,根据自由落体
运的速度公式v=gt可知,它在1 s末和2 s末的
速度大小分别为v1=9.8 m/s和v2=19.6 m/s.显然,
v2=2v1 ,并且方向都是竖直向下.
数乘运算的定义
课文精讲
以上实例说明在实际中存在这样的两个
向量,它们是共线的,而且大小之间具有倍
数关系.因此,有必要定义实数与向量的乘积
运算.
数乘运算的定义
课文精讲
数乘运算的定义
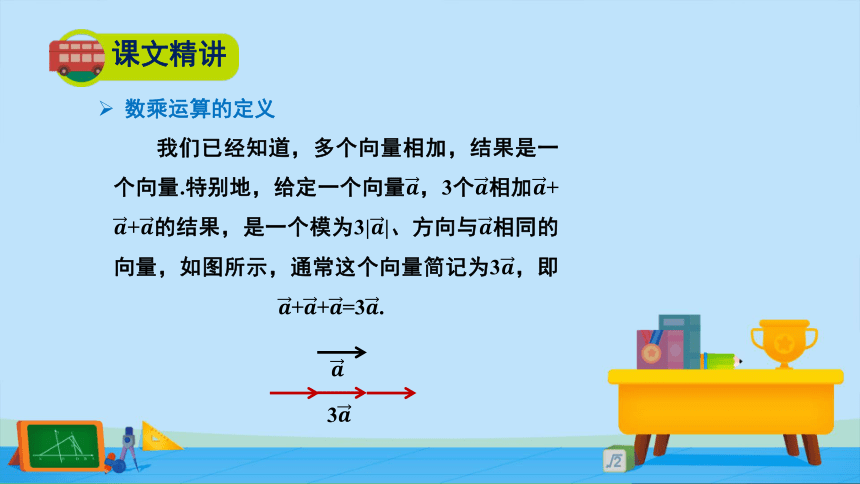
我们已经知道,多个向量相加,结果是一
个向量.特别地,给定一个向量????,3个????相加????+
????+????的结果,是一个模为3|????|、方向与????相同的
向量,如图所示,通常这个向量简记为3????,即
????+????+????=3????.
?
????
?
3????
?
课文精讲
数乘运算的定义
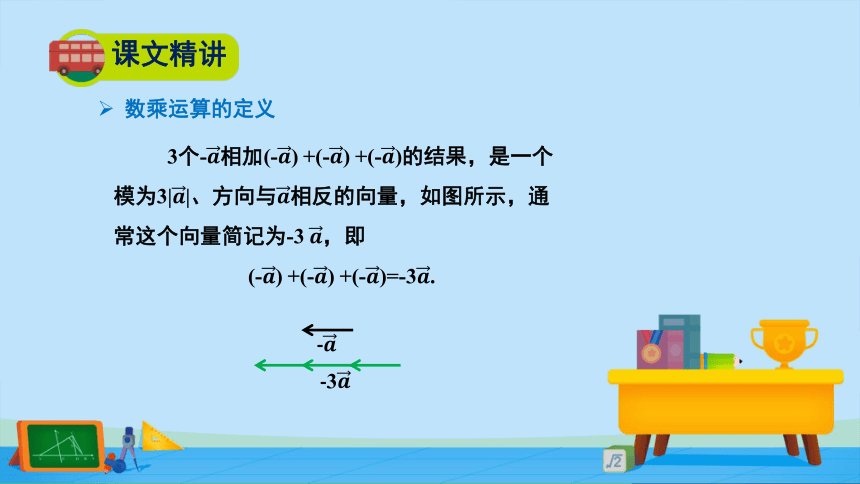
3个-????相加(-????)?+(-????) +(-????)的结果,是一个
模为3|????|、方向与????相反的向量,如图所示,通
常这个向量简记为-3 ????,即
(-????)?+(-????) +(-????)=-3????.
?
-????
?
-3????
?
课文精讲
数乘运算的定义
实数λ与向量????的乘积是一个向量,记作
λ????,满足以下条件:
(1)当λ>0时,向量λ????与向量????的方向相同;
当λ<0时,向量λ????与向量????的方向相反;
当λ=0时,0 ????= ????.
(2)| λ???? |= |λ|| ????|.
?
这种运算称为向量的数乘.
课文精讲
如图,由实数与向量数乘λ????的定义可以看
出,它的几何意义是:
(1)当λ >0时,表示向量????的有向线段在原方向
伸长或缩短为原来的| λ |倍;
(2)当λ <0时,表示向量????的有向线段在反方向
伸长或缩短为原来的| λ |倍.
?
数乘运算的定义
????
?
λ????
?
λ????
?
λ >0
λ <0
课文精讲
由向量的数乘定义容易推出,在非零向量
????方向上的单位向量是
????|????|.
?
数乘运算的定义
它表明一个非零向量除以它的模(乘它的
模的倒数)的结果是一个与原向量同方向的单
位向量,这一过程称为向量的单位化.
????
?
λ????
?
λ????
?
λ >0
λ <0
课文精讲
设λ,μ为实数, ????, ????为向量,那么根据
向量的数乘定义,可以得到以下运算律:
?
数乘运算的运算律
(1)(λ+ μ)????= λ????+ μ????;
(2)λ (μ????)=?(λ μ)?????;
(3)λ(?????+ ????)=λ????+ λ????.
?
结合律
第一分配率
第二分配率
课文精讲
特别地,我们有:
数乘运算的运算律
(-λ)????=-(λ????) = λ(-????)
λ(?????- ????)=λ????- λ????
?
结合律
分配率
课文精讲
利用相似三角形的性质,从下图,可以推出运算律(3),其他运算律可以由向量的数乘定义直接得到.
数乘运算的运算律
?????+ ????
?
????
?
????
?
λ????
?
λ????
?
λ????+ λ????
?
λ(?????+ ????)
?
λ>0
λ<0
λ????+ λ????
?
λ????
?
????
?
????
?
?????+ ????
?
λ(?????+ ????)
?
λ????
?
课文精讲
向量的加法、减法和数乘的综合运算,
通常称为向量的线性运算(或线性组合).例如,
2????+3????,-3????+5????, ????????????- ????????????等都是????,????的线性
运算.若一个向量????由向量????, ????的线性运算得
到,如?????= 2????+3?????,则称向量????可以用向量????,
????线性表示.
?
数乘运算的运算律
课文精讲
向量的数乘运算相当于代数的多项式运
算,主要包括“合并同类项”和“提取公因
式”.
但是代数的多项式运算是一个实数,向
量的数乘运算是一个向量.
数乘运算的运算律
典型例题
例1:设????, ????为向量,计算下列各式:
(1) (-3)?×4????;
(2) 3(?????+ ????)- ???????? (?????- ????)-????;
(3) (2λ- μ)????- λ????- (λ- μ) (?????- ????)(λ, μ为实数).
?
典型例题
例1:设????, ????为向量,计算下列各式:
(1) (-3)?×4????;
?
解:(1) 由数乘运算的运算律,得
(-3)?×4????= (-3×4) ????=-12????;
?
典型例题
例1:设????, ????为向量,计算下列各式:
(2) 3(?????+ ????)- ???????? (?????- ????)-????;
?
解:(2) 由数乘运算的运算律,得
3(?????+ ????)- ???????? (?????- ????)-????=3?????+3????- ????????????+ ????????????- ????
=????????????+????????????;
?
典型例题
例1:设????, ????为向量,计算下列各式:
(3) (2λ- μ)????- λ????- (λ- μ) (?????- ????)(λ, μ为实数).
?
解:(3) 由数乘运算的运算律,得
(2λ- μ)????- λ????- (λ- μ) (????-????)
=2λ????- μ????-λ????-λ(?????- ????)+μ(????-????)
=2λ????- μ????-λ????-λ?????+λ????+μ????-μ????
= λ????-μ????.
?
典型例题
例2:设????是未知向量,解方程????+????-3 (???? - ????)=????.
?
解:原式可变形为????+????-3???? + 3????=????,
2????=????+3????,
????= ???????? ????+ ????????????.
?
典型例题
例3:如图,已知点O是△ABC所在平面内一点,
点D为边BC的中点,且????????+????????+????????=????,说明
向量???????? 与????????的关系.
?
解:因为点D为BC边的中点,所以????????+ ????????=2????????.
又????????+????????+????????=????,所以????????+2 ????????= ????.
也就是2 ???????? =- ????????, ????????= ?????????????????.
?
O
B
C
A
D
典型例题
例3:如图,已知点O是△ABC所在平面内一点,
点D为边BC的中点,且????????+????????+????????=????,说明
向量???????? 与????????的关系.
?
解:所以????????= ????????+ ????????= ???????? ????????,即向量????????与????????共线且方向相同,长度是向量长度的????????倍.
?
O
B
C
A
D
综合练习
已知????=?????????+2?????????, ????= ?????????-2?????????,则2????-3????=___________.
?
解:已知????=?????????+2?????????, ????= ?????????-2?????????,
则2????-3????=2 ?????????+4????????-3?????????+6????????=- ?????????+10????????.
?
- ?????????+10????????
?
综合练习
已知????????=2?????????,????????=m?????????,则m=_______.
?
解:因为????????=2?????????,????????=m?????????,
所以????????=m(?????????+ ?????????)= -m????????-m????????,
可得(1+ m) ????????=-m ????????,
可得????????=????+????????? ?????????,
所以????+????????? =2,可得????=-????????.
?
- ????????
?
本课小结
再 见
授课教师:
温故知新
学习目标
1.理解数乘向量的概念及其几何意义;(重点)
2.掌握数乘向量的运算律,能进行简单运算.(难
点)
课文精讲
在疾风骤雨、雷电交加的夜晚,为什么我
们总是先看到闪电,后听到雷声?这是因为光
速远远大于声速.经测量,光速大小约为声速
的8.8×105倍.
数乘运算的定义
课文精讲
一重物由高空自由落下,根据自由落体
运的速度公式v=gt可知,它在1 s末和2 s末的
速度大小分别为v1=9.8 m/s和v2=19.6 m/s.显然,
v2=2v1 ,并且方向都是竖直向下.
数乘运算的定义
课文精讲
以上实例说明在实际中存在这样的两个
向量,它们是共线的,而且大小之间具有倍
数关系.因此,有必要定义实数与向量的乘积
运算.
数乘运算的定义
课文精讲
数乘运算的定义
我们已经知道,多个向量相加,结果是一
个向量.特别地,给定一个向量????,3个????相加????+
????+????的结果,是一个模为3|????|、方向与????相同的
向量,如图所示,通常这个向量简记为3????,即
????+????+????=3????.
?
????
?
3????
?
课文精讲
数乘运算的定义
3个-????相加(-????)?+(-????) +(-????)的结果,是一个
模为3|????|、方向与????相反的向量,如图所示,通
常这个向量简记为-3 ????,即
(-????)?+(-????) +(-????)=-3????.
?
-????
?
-3????
?
课文精讲
数乘运算的定义
实数λ与向量????的乘积是一个向量,记作
λ????,满足以下条件:
(1)当λ>0时,向量λ????与向量????的方向相同;
当λ<0时,向量λ????与向量????的方向相反;
当λ=0时,0 ????= ????.
(2)| λ???? |= |λ|| ????|.
?
这种运算称为向量的数乘.
课文精讲
如图,由实数与向量数乘λ????的定义可以看
出,它的几何意义是:
(1)当λ >0时,表示向量????的有向线段在原方向
伸长或缩短为原来的| λ |倍;
(2)当λ <0时,表示向量????的有向线段在反方向
伸长或缩短为原来的| λ |倍.
?
数乘运算的定义
????
?
λ????
?
λ????
?
λ >0
λ <0
课文精讲
由向量的数乘定义容易推出,在非零向量
????方向上的单位向量是
????|????|.
?
数乘运算的定义
它表明一个非零向量除以它的模(乘它的
模的倒数)的结果是一个与原向量同方向的单
位向量,这一过程称为向量的单位化.
????
?
λ????
?
λ????
?
λ >0
λ <0
课文精讲
设λ,μ为实数, ????, ????为向量,那么根据
向量的数乘定义,可以得到以下运算律:
?
数乘运算的运算律
(1)(λ+ μ)????= λ????+ μ????;
(2)λ (μ????)=?(λ μ)?????;
(3)λ(?????+ ????)=λ????+ λ????.
?
结合律
第一分配率
第二分配率
课文精讲
特别地,我们有:
数乘运算的运算律
(-λ)????=-(λ????) = λ(-????)
λ(?????- ????)=λ????- λ????
?
结合律
分配率
课文精讲
利用相似三角形的性质,从下图,可以推出运算律(3),其他运算律可以由向量的数乘定义直接得到.
数乘运算的运算律
?????+ ????
?
????
?
????
?
λ????
?
λ????
?
λ????+ λ????
?
λ(?????+ ????)
?
λ>0
λ<0
λ????+ λ????
?
λ????
?
????
?
????
?
?????+ ????
?
λ(?????+ ????)
?
λ????
?
课文精讲
向量的加法、减法和数乘的综合运算,
通常称为向量的线性运算(或线性组合).例如,
2????+3????,-3????+5????, ????????????- ????????????等都是????,????的线性
运算.若一个向量????由向量????, ????的线性运算得
到,如?????= 2????+3?????,则称向量????可以用向量????,
????线性表示.
?
数乘运算的运算律
课文精讲
向量的数乘运算相当于代数的多项式运
算,主要包括“合并同类项”和“提取公因
式”.
但是代数的多项式运算是一个实数,向
量的数乘运算是一个向量.
数乘运算的运算律
典型例题
例1:设????, ????为向量,计算下列各式:
(1) (-3)?×4????;
(2) 3(?????+ ????)- ???????? (?????- ????)-????;
(3) (2λ- μ)????- λ????- (λ- μ) (?????- ????)(λ, μ为实数).
?
典型例题
例1:设????, ????为向量,计算下列各式:
(1) (-3)?×4????;
?
解:(1) 由数乘运算的运算律,得
(-3)?×4????= (-3×4) ????=-12????;
?
典型例题
例1:设????, ????为向量,计算下列各式:
(2) 3(?????+ ????)- ???????? (?????- ????)-????;
?
解:(2) 由数乘运算的运算律,得
3(?????+ ????)- ???????? (?????- ????)-????=3?????+3????- ????????????+ ????????????- ????
=????????????+????????????;
?
典型例题
例1:设????, ????为向量,计算下列各式:
(3) (2λ- μ)????- λ????- (λ- μ) (?????- ????)(λ, μ为实数).
?
解:(3) 由数乘运算的运算律,得
(2λ- μ)????- λ????- (λ- μ) (????-????)
=2λ????- μ????-λ????-λ(?????- ????)+μ(????-????)
=2λ????- μ????-λ????-λ?????+λ????+μ????-μ????
= λ????-μ????.
?
典型例题
例2:设????是未知向量,解方程????+????-3 (???? - ????)=????.
?
解:原式可变形为????+????-3???? + 3????=????,
2????=????+3????,
????= ???????? ????+ ????????????.
?
典型例题
例3:如图,已知点O是△ABC所在平面内一点,
点D为边BC的中点,且????????+????????+????????=????,说明
向量???????? 与????????的关系.
?
解:因为点D为BC边的中点,所以????????+ ????????=2????????.
又????????+????????+????????=????,所以????????+2 ????????= ????.
也就是2 ???????? =- ????????, ????????= ?????????????????.
?
O
B
C
A
D
典型例题
例3:如图,已知点O是△ABC所在平面内一点,
点D为边BC的中点,且????????+????????+????????=????,说明
向量???????? 与????????的关系.
?
解:所以????????= ????????+ ????????= ???????? ????????,即向量????????与????????共线且方向相同,长度是向量长度的????????倍.
?
O
B
C
A
D
综合练习
已知????=?????????+2?????????, ????= ?????????-2?????????,则2????-3????=___________.
?
解:已知????=?????????+2?????????, ????= ?????????-2?????????,
则2????-3????=2 ?????????+4????????-3?????????+6????????=- ?????????+10????????.
?
- ?????????+10????????
?
综合练习
已知????????=2?????????,????????=m?????????,则m=_______.
?
解:因为????????=2?????????,????????=m?????????,
所以????????=m(?????????+ ?????????)= -m????????-m????????,
可得(1+ m) ????????=-m ????????,
可得????????=????+????????? ?????????,
所以????+????????? =2,可得????=-????????.
?
- ????????
?
本课小结
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
