2.3.2向量的数乘与向量共线的关系-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(23张PPT)
文档属性
| 名称 | 2.3.2向量的数乘与向量共线的关系-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 835.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 18:02:22 | ||
图片预览







文档简介
向量的数乘与向量共线的关系
授课教师:
温故知新
学习目标
1.掌握共线向量基本定理,并会简单应用;(重
点)
2.掌握直线的向量表示.(重点)
课文精讲
设????是非零向量.由向量共线和数乘的定义
可以直接推知,对于任意向量????. 若????=λ ????, λ是
一个实数,则????∥ ????.反之,对于任意向量????,
若????∥ ????,是否存在一个实数λ ,使得????=λ ?????
?
共线(平行)向量基本定理
课文精讲
可以分以下两种情况讨论.
共线(平行)向量基本定理
若????和????方向相同,则 是????的单位向量,
????=|????| ,即????= ,λ= ;
?
????|????|
?
????|????|
?
|????||????|
?
????
?
|????||????|
?
若????和????方向相反,则 是????的单位向量,
????=?|????| ,即????=? ,λ=? .
?
?????|????|
?
????|????|
?
????
?
|????||????|
?
|????||????|
?
所以一定存在唯一一个实数λ,使????= λ????.
?
课文精讲
这样就得到如下定理:
共线(平行)向量基本定理 给定一个非
零向量????,则对于任意向量?????, ?????∥????的充要
条件是存在唯一一个实数λ,使 ?????= λ????.
例如,????=?2 ????,则????∥????;若????∥????, ????的
长度是????的2倍并且方向相反,则?????=?2????.
?
共线(平行)向量基本定理
课文精讲
共线(平行)向量基本定理
在共线向量基本定理中:
(1) ?????= λ????时,通常称为????能用????表示.
(2)其中的“唯一”指的是,如果还有????=μ????,
则λ=μ.这是因为:由λ????= μ????可知(λ-μ) ????=????,
如果λ-μ ≠0,则????= ????,与已知矛盾,所以
λ-μ=0,即λ=μ.
?
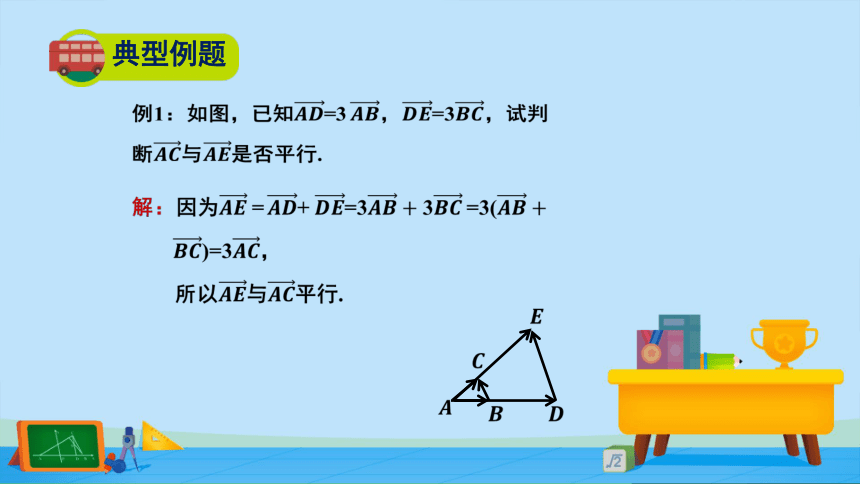
典型例题
例1:如图,已知????????=3 ????????,????????=3????????,试判
断????????与????????是否平行.
?
解:因为?????????= ????????+ ????????=3????????+?????????????=3(????????+????????)=3????????,
所以????????与????????平行.
?
????
?
????
?
????
?
????
?
????
?
典型例题
例2:设A,B,C,D中的任何三个点不共线,
用向量语言描述下列几何图形的特征.
(1)四边形ABCD是平行四边形;
(2)在梯形ABCD中,上底AD长是下底BC长的
一半;
(3)点D是△ABC的重心.
典型例题
例2:设A,B,C,D中的任何三个点不共线,
用向量语言描述下列几何图形的特征.
(1)四边形ABCD是平行四边形;
解:共线(平行)向量基本定理,得
(1) ????????=?????????且????????=????????(如图①).
?
A
B
C
D
①
典型例题
例2:设A,B,C,D中的任何三个点不共线,
用向量语言描述下列几何图形的特征.
(2)在梯形ABCD中,上底AD长是下底BC长的
一半;
解:共线(平行)向量基本定理,得
(2) ????????=????????????????(如图②).
?
A
B
C
D
②
典型例题
例2:设A,B,C,D中的任何三个点不共线,
用向量语言描述下列几何图形的特征.
(3)点D是△ABC的重心.
解:共线(平行)向量基本定理,得
(3) ????????=??????????(????????+????????)或????????=??????????(????????+????????)
或????????=??????????(????????+????????) ;也可以表示成
????????+????????+????????= ????(如图③).
?
B
A
C
D
③
课文精讲
直线的向量表示
能否用向量来刻画直线呢?
问题提出
课文精讲
直线的向量表示
如图,已知A,B两点确定一条直线l,直
线l上任意一点P所对应的向量????????与向量????????平
行,从而????????可以用????????表示,即存在唯一实数
t,使得?????????=t ????????.这说明由一个点A和一个非
零向量????????可以唯一地确定过点A与向量????????平
行的直线l.
?
分析理解
A
B
l
P
·
课文精讲
直线的向量表示
通常可以用?????????=t ????????表示过点A,B的直线l,其中????????称为直线l的方向向量.
?
典型例题
例3:如图,已知A,B是直线l上的两个定点,
点O是直线l外的一个定点,点P是直线l上的
任意一点.证明:存在唯一的实数t,满足?????????=
?????????+t ????????.
?
解:因为A,B, P都是直线l上的点,所以存在唯一实数t,使得?????????=t ?????????,
因为?????????= ?????????- ????????,
所以?????????-?????????=t ????????.
即?????????= ?????????+t ????????.
?
A
B
P
l
O
典型例题
例3:如图,已知A,B是直线l上的两个定点,
点O是直线l外的一个定点,点P是直线l上的
任意一点.证明:存在唯一的实数t,满足?????????=
?????????+t ????????.
?
本题给出了利用直线的向量表示来判断A,
B, P三点共线的一种方法.
A
B
P
l
O
典型例题
在例3中,若点P是AB的中点,则?????????=
???????? (?????????+ ????????),这是线段AB中点的向量表达式.
?
直线的向量表示
综合练习
忽视零向量
判断向量????=?2?????,????=5?????是否共线.
?
解:当?????= ?????时, ????= ????= ?????,所以????与????共线;
当?????≠ ?????时,由于????= ???????????,所以存在唯一
实数λ= ????????? ,使得????=λ?????,从而????与????共线.
综上,向量????与????共线.
?
忽视零向量
误区警示:
判断两个向量是否共线的关键是看两个向量是否满足向量共线定理. 在向量共线定理????=λ????中要求????≠ ????. 因此. 在解相关问题时,不要忽略零向量.
?
综合练习
综合练习
已知????与????不共线,而且????-x????与3????+ 2????共线,求
x的值.
?
解: 因为????与????不共线,所以3????+ 2????≠ ????,因此
由已知可得存在实数t,使得
????-x????=t(3????+2????),
即????-x????=t(3????+2????),从而
?
1=3t,
-x=2t,
x=?????????.
?
本课小结
再 见
授课教师:
温故知新
学习目标
1.掌握共线向量基本定理,并会简单应用;(重
点)
2.掌握直线的向量表示.(重点)
课文精讲
设????是非零向量.由向量共线和数乘的定义
可以直接推知,对于任意向量????. 若????=λ ????, λ是
一个实数,则????∥ ????.反之,对于任意向量????,
若????∥ ????,是否存在一个实数λ ,使得????=λ ?????
?
共线(平行)向量基本定理
课文精讲
可以分以下两种情况讨论.
共线(平行)向量基本定理
若????和????方向相同,则 是????的单位向量,
????=|????| ,即????= ,λ= ;
?
????|????|
?
????|????|
?
|????||????|
?
????
?
|????||????|
?
若????和????方向相反,则 是????的单位向量,
????=?|????| ,即????=? ,λ=? .
?
?????|????|
?
????|????|
?
????
?
|????||????|
?
|????||????|
?
所以一定存在唯一一个实数λ,使????= λ????.
?
课文精讲
这样就得到如下定理:
共线(平行)向量基本定理 给定一个非
零向量????,则对于任意向量?????, ?????∥????的充要
条件是存在唯一一个实数λ,使 ?????= λ????.
例如,????=?2 ????,则????∥????;若????∥????, ????的
长度是????的2倍并且方向相反,则?????=?2????.
?
共线(平行)向量基本定理
课文精讲
共线(平行)向量基本定理
在共线向量基本定理中:
(1) ?????= λ????时,通常称为????能用????表示.
(2)其中的“唯一”指的是,如果还有????=μ????,
则λ=μ.这是因为:由λ????= μ????可知(λ-μ) ????=????,
如果λ-μ ≠0,则????= ????,与已知矛盾,所以
λ-μ=0,即λ=μ.
?
典型例题
例1:如图,已知????????=3 ????????,????????=3????????,试判
断????????与????????是否平行.
?
解:因为?????????= ????????+ ????????=3????????+?????????????=3(????????+????????)=3????????,
所以????????与????????平行.
?
????
?
????
?
????
?
????
?
????
?
典型例题
例2:设A,B,C,D中的任何三个点不共线,
用向量语言描述下列几何图形的特征.
(1)四边形ABCD是平行四边形;
(2)在梯形ABCD中,上底AD长是下底BC长的
一半;
(3)点D是△ABC的重心.
典型例题
例2:设A,B,C,D中的任何三个点不共线,
用向量语言描述下列几何图形的特征.
(1)四边形ABCD是平行四边形;
解:共线(平行)向量基本定理,得
(1) ????????=?????????且????????=????????(如图①).
?
A
B
C
D
①
典型例题
例2:设A,B,C,D中的任何三个点不共线,
用向量语言描述下列几何图形的特征.
(2)在梯形ABCD中,上底AD长是下底BC长的
一半;
解:共线(平行)向量基本定理,得
(2) ????????=????????????????(如图②).
?
A
B
C
D
②
典型例题
例2:设A,B,C,D中的任何三个点不共线,
用向量语言描述下列几何图形的特征.
(3)点D是△ABC的重心.
解:共线(平行)向量基本定理,得
(3) ????????=??????????(????????+????????)或????????=??????????(????????+????????)
或????????=??????????(????????+????????) ;也可以表示成
????????+????????+????????= ????(如图③).
?
B
A
C
D
③
课文精讲
直线的向量表示
能否用向量来刻画直线呢?
问题提出
课文精讲
直线的向量表示
如图,已知A,B两点确定一条直线l,直
线l上任意一点P所对应的向量????????与向量????????平
行,从而????????可以用????????表示,即存在唯一实数
t,使得?????????=t ????????.这说明由一个点A和一个非
零向量????????可以唯一地确定过点A与向量????????平
行的直线l.
?
分析理解
A
B
l
P
·
课文精讲
直线的向量表示
通常可以用?????????=t ????????表示过点A,B的直线l,其中????????称为直线l的方向向量.
?
典型例题
例3:如图,已知A,B是直线l上的两个定点,
点O是直线l外的一个定点,点P是直线l上的
任意一点.证明:存在唯一的实数t,满足?????????=
?????????+t ????????.
?
解:因为A,B, P都是直线l上的点,所以存在唯一实数t,使得?????????=t ?????????,
因为?????????= ?????????- ????????,
所以?????????-?????????=t ????????.
即?????????= ?????????+t ????????.
?
A
B
P
l
O
典型例题
例3:如图,已知A,B是直线l上的两个定点,
点O是直线l外的一个定点,点P是直线l上的
任意一点.证明:存在唯一的实数t,满足?????????=
?????????+t ????????.
?
本题给出了利用直线的向量表示来判断A,
B, P三点共线的一种方法.
A
B
P
l
O
典型例题
在例3中,若点P是AB的中点,则?????????=
???????? (?????????+ ????????),这是线段AB中点的向量表达式.
?
直线的向量表示
综合练习
忽视零向量
判断向量????=?2?????,????=5?????是否共线.
?
解:当?????= ?????时, ????= ????= ?????,所以????与????共线;
当?????≠ ?????时,由于????= ???????????,所以存在唯一
实数λ= ????????? ,使得????=λ?????,从而????与????共线.
综上,向量????与????共线.
?
忽视零向量
误区警示:
判断两个向量是否共线的关键是看两个向量是否满足向量共线定理. 在向量共线定理????=λ????中要求????≠ ????. 因此. 在解相关问题时,不要忽略零向量.
?
综合练习
综合练习
已知????与????不共线,而且????-x????与3????+ 2????共线,求
x的值.
?
解: 因为????与????不共线,所以3????+ 2????≠ ????,因此
由已知可得存在实数t,使得
????-x????=t(3????+2????),
即????-x????=t(3????+2????),从而
?
1=3t,
-x=2t,
x=?????????.
?
本课小结
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
