2.6.1余弦定理与正弦定理-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(76张PPT)
文档属性
| 名称 | 2.6.1余弦定理与正弦定理-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(76张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 18:09:41 | ||
图片预览









文档简介
余弦定理与正弦定理
授课教师:
温故知新
学习目标
1.通过对特殊三角形边角间数量关系的研究,发
现余弦定理与正弦定理,并了解其向量证法;(难点)
2.掌握余弦定理与正弦定理,并能运用其解三角
形.(重点)
课文精讲
问题提出
三角形中边角关系很丰富,本节继续研究.
如已知两边及其夹角,怎么求出此角的对边呢?
已知三条边,又怎么求出它的三个角呢?
余弦定理
课文精讲
分析理解
我们利用向量来研究.
如图,在△ABC中,设|????????|=a,|????????|=b,
|????????|=c,根据向量的数量积,可得
?
余弦定理
a2= ????????· ????????=(????????-????????)·(????????-????????)
=|????????|2-2|????????|·|????????|cosA+|????????|2
=b2-2bccosA+c2,
即a2= b2+c2-2bccosA.
?
A
B
C
a
c
b
课文精讲
余弦定理 三角形任何一边的平方等于其他
两边的平方和减去这两边与它们
夹角余弦的积的两倍,即
余弦定理
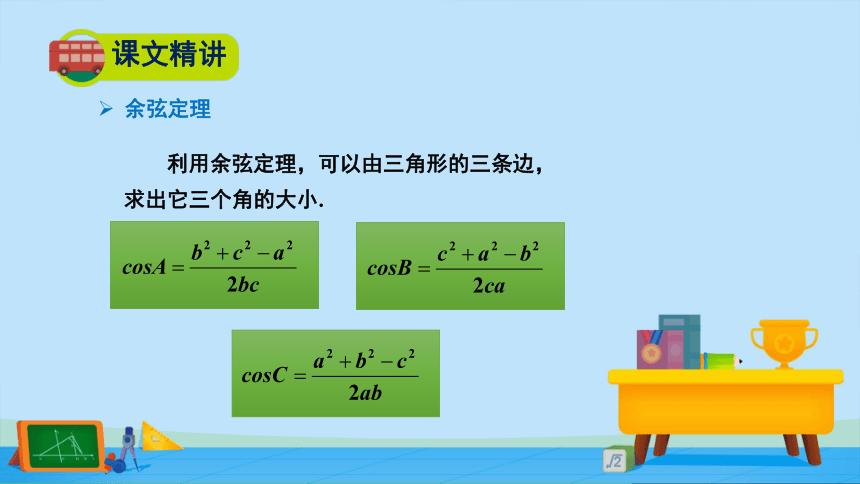
a2=b2+c2-2bccosA
b2=a2+c2-2accosB
c2=a2+b2-2abcosC
课文精讲
利用余弦定理,可以由三角形的三条边,
求出它三个角的大小.
余弦定理
典型例题
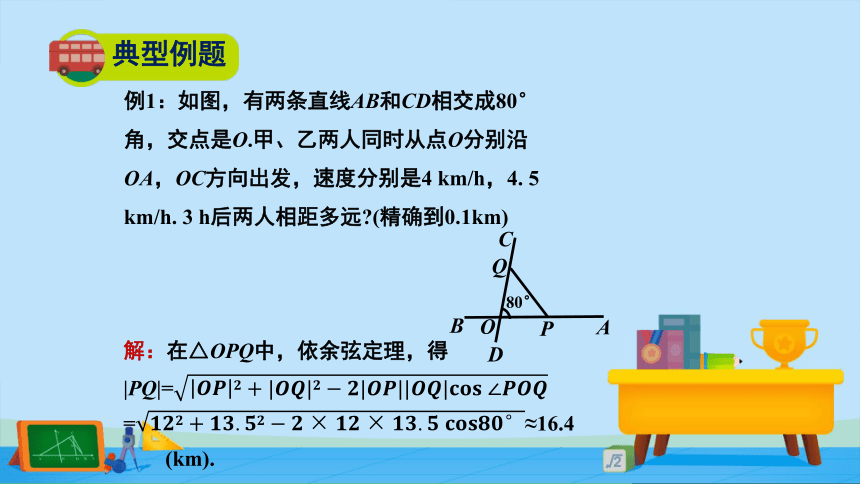
例1:如图,有两条直线AB和CD相交成80°
角,交点是O.甲、乙两人同时从点O分别沿
OA,OC方向出发,速度分别是4 km/h,4. 5
km/h. 3 h后两人相距多远?(精确到0.1km)
解:经过3 h,甲到达点P,|OP|=4×3=12(km),
乙到达点Q,|OQ|=4.5×3=13.5(km).
A
C
O
B
D
P
Q
80°
典型例题
例1:如图,有两条直线AB和CD相交成80°
角,交点是O.甲、乙两人同时从点O分别沿
OA,OC方向出发,速度分别是4 km/h,4. 5
km/h. 3 h后两人相距多远?(精确到0.1km)
解:在△OPQ中,依余弦定理,得
|PQ|=????????????+|????????|?????????|????????||????????|?????????????∠????????????
=????????????+????????.?????????????×????????×????????.?????????????????????????°≈16.4(km).
?
A
C
O
B
D
P
Q
80°
典型例题
例1:如图,有两条直线AB和CD相交成80°
角,交点是O.甲、乙两人同时从点O分别沿
OA,OC方向出发,速度分别是4 km/h,4. 5
km/h. 3 h后两人相距多远?(精确到0.1km)
解:因此,3 h后两人相距约16.4 km.
A
C
O
B
D
P
Q
80°
典型例题
解:在△BCD中,BC=1,CD=1,∠BCD=135°,
BD2=BC2+CD2-2BC·CDcos∠BCD
12+12-2×1×1cos135°=2+????.
所以BD≈1.8.
?
例2:如图是古希腊数学家特埃特图斯用来构
造无理数????, ?????, ?????,···的图形.试计算图
中线段BD的长度及∠DAB的大小.(长度精确到
0.1,角度精确到1°)
?
A
B
C
D
1
1
1
????
?
????
?
典型例题
解:在△ABD中,AB=1,BD=????+????,AD=????,
cos∠DAB=????????+(????)?????(????+????)????×????×????
=??????????????????≈0.1691.
?
例2:如图是古希腊数学家特埃特图斯用来构
造无理数????, ?????, ?????,···的图形.试计算图
中线段BD的长度及∠DAB的大小.(长度精确到
0.1,角度精确到1°)
?
所以∠DAB≈80°.
A
B
C
D
1
1
1
????
?
????
?
典型例题
解:由A是锐角,且cos2A=-????????,得2A=????????????,A=????????.
?
例3:在△ABC中,a,b,c分别是角A,B,C
的对边,已知A是锐角,且cos2A=-????????.
(1)若mbc=b2+c2-a2,求实数m的值;
(2)若a=????,求△ABC面积的最大值.
?
(1) mbc=b2+c2-a2,可变形为????????+?????????????????????????????=????????.
依据余弦定理,可知cosA=????????+?????????????????????????????=????????,????????=????????,所以m=1.
?
典型例题
解:
例3:在△ABC中,a,b,c分别是角A,B,C
的对边,已知A是锐角,且cos2A=-????????.
(1)若mbc=b2+c2-a2,求实数m的值;
(2)若a=????,求△ABC面积的最大值.
?
(2) 因为sinA=sin????????=????????,
所以bc= b2+c2-a2≥2bc-a2,
即bc≤a2.故S △ABC=????????????sinA
≤ ?????????????· ????????=????????????.
?
S △ABC=???????? ch=????????cbsinA
?
A
B
C
c
b
h
典型例题
解:(2)即所求△ABC面积的最大值是????????????.
?
例3:在△ABC中,a,b,c分别是角A,B,C
的对边,已知A是锐角,且cos2A=-????????.
(1)若mbc=b2+c2-a2,求实数m的值;
(2)若a=????,求△ABC面积的最大值.
?
S △ABC=???????? ch=????????cbsinA
?
A
B
C
c
b
h
课文精讲
问题提出
如图,若△ABC是直角三角形,C=90°,
则由sinA=-????????,sinB=-????????,
可知 ????????????????????=????????????????????=c.
因为C=90°,sinC=1,
所以????????????????????=????????????????????=????????????????????.
?
正弦定理
C
B
A
b
c
a
课文精讲
对等边三角形,这个等式无疑也成立;对
其他三角形,它是否仍然成立呢?
正弦定理
C
B
A
b
c
a
课文精讲
分析理解
如图,△ABC是锐角三角形,CD是边AB
上的高,根据三角函数的定义,
CD=asinB,
CD=bsinA,
所以????????????????????=????????????????????.
?
正弦定理
B
A
C
D
a
b
课文精讲
分析理解
同理 ????????????????????=????????????????????.
即????????????????????=????????????????????=????????????????????.
?
正弦定理
因此,对锐角三角形,以上等式仍然成立.
B
A
C
D
a
b
课文精讲
探究:当△ABC是钝角三角形时,以上等式是
否仍然成立?
正弦定理
成立
课文精讲
正弦定理 在一个三角形中,各边和它所对
角的正弦的比相等,即
正弦定理
????????????????????=????????????????????=????????????????????
?
运用由特殊到一般的方法发现了正弦定理,
这种思想方法经常用于发现客观规律.
典型例题
例4:某地出土一块古代玉佩(如图),其一角
已破损,现测得如下数据:BC=2.57 cm,
CE=3. 57 cm,BD=4.38 cm,B=450,
C=120°.为了复原,请计算原玉佩另两边的
长.(精确到0. 01 cm)
D
E
B
C
典型例题
例4:某地出土一块古代玉佩(如图),其一角
已破损,现测得如下数据:BC=2.57 cm,
CE=3. 57 cm,BD=4.38 cm,B=45°,
C=120°.为了复原,请计算原玉佩另两边的
长.(精确到0. 01 cm)
解:将BD,CE分别延长
相交于点A(如图),
在△ABC中,BC=2.57 cm,
B=45°,C=120°,
A=180°-(B+C)=180°- (45°+120°)=15°.
D
E
B
C
A
典型例题
例4:某地出土一块古代玉佩(如图),其一角
已破损,现测得如下数据:BC=2.57 cm,
CE=3. 57 cm,BD=4.38 cm,B=45°,
C=120°.为了复原,请计算原玉佩另两边的
长.(精确到0. 01 cm)
解:由正弦定理,得
????????????????????????=???????????????????????? ,
?
所以
AC=????????????????????????????????????????=????.????????????????????????????°????????????????????° ≈7.02(cm),
?
D
E
B
C
A
典型例题
例4:某地出土一块古代玉佩(如图),其一角
已破损,现测得如下数据:BC=2.57 cm,
CE=3. 57 cm,BD=4.38 cm,B=45°,
C=120°.为了复原,请计算原玉佩另两边的
长.(精确到0. 01 cm)
解:同理AB≈8.60(cm).
因此,原玉佩另两边的长
分别约为7.02 cm,8.60 cm.
D
E
B
C
A
典型例题
例5:求证:如图(1),以Rt△ABC斜边AB为
直径作外接圆,设这个外接圆的半径为R,则
????????????????????=????????????????????=????????????????????=2R.
?
证明:在Rt△ABC中,C=90°,????????????????????=c,
又????????????????????=????????????????????=????????????????????,且c=2R,
所以????????????????????=????????????????????=????????????????????=2R.
?
(1)
C
B
A
·
课文精讲
思考
对于钝角三角形(如图(2))、锐角三角形
(如图(3)),上述结论还成立吗?
(2)
B
B
A
·
C
(3)
B
A
·
C
B′
B′
成立
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:如图,设台风中心从点B向西北方向沿射
线BD移动,该市位于点B正西
方向300 km处的点A.
D
A
B
北
东
C
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:假设经过t h,台风中心到达点C.在△ABC
中,AB=300 km, AC=250 km,
BC=40t km,B=45°.
D
A
B
北
东
C
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:由正弦定理,得????????????????????????=????????????????????????=????????????????????????,
????????????????=?????????????????????????????????=????????????????????????????????°????????????
≈0.8485.
?
D
A
B
北
东
C
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:所以角C有两个解(如图①):
∠AC1B≈121.95°,
∠AC2B≈58.05°.
图①
D
A
B
北
东
C2
C1
E
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:当∠AC1B≈121.95°时,
∠C1AB=180°-(B+∠ AC1B)
≈180°-(45°+121.95°)
=13.05°.
图①
D
A
B
北
东
C2
C1
E
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:从而BC1=????????????????????????????????????????????
=????????????????????????????????.????????°????????????????????°
=250????sin13.05°(km),
?
图①
D
A
B
北
东
C2
C1
E
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:t1=?????????????????????=????????????????????????????????????.????????°????????
≈2.00?(h).
?
图①
D
A
B
北
东
C2
C1
E
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:同理,当∠AC2B≈58.05°时,
BC2=250????sin76.95° km,
t2 ≈8.61 h.
t2 - t1 ≈8.61-2.00≈6.6(h).
?
图①
D
A
B
北
东
C2
C1
E
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:因此,约2h后将要遭受台风影
响,持续约6.6 h.
图①
D
A
B
北
东
C2
C1
E
谢 谢
课文精讲
思考:
已知两条边的边长和其中一条边的对角的大小解三角形,它的解有几种情况?
课文精讲
正弦定理、余弦定理是两个重要定理,在
解决与三角形有关的几何计算问题中有着广泛的应用.
用正弦定理、余弦定理解三角形
在三角形的三条边和三个角这6个元素中,
如果已知3个(至少含一边长),那么由余弦定
理和正弦定理,就可以求得其他3个元素.具体
情形如下:
课文精讲
情形1:已知两个角的大小和一条边的边长.
先由三角形内角和等于180°求出第三个
角的大小,然后依据正弦定理求得另外两条
的边长.
用正弦定理、余弦定理解三角形
情形2:已知两条边的边长及其夹角的大小.
先由余弦定理求出第三条边的边长,然
后再由余弦定理求得第二、第三个角的大小.
课文精讲
情形3:已知三条边的边长.
由余弦定理求出两个角,再利用三角形内
角和等于180°求出第三个角.
用正弦定理、余弦定理解三角形
课文精讲
用正弦定理、余弦定理解三角形
情形4:已知两条边的边长和其中一边对角的
大小.
首先,由正弦定理求出第二条边所对角的
正弦,这时,要判断是两解、一解还是无解.
然后,根据三角形内角和等于180°得到第三个
角的大小.最后,由余弦定理或正弦定理求得第三条边的边长.
典型例题
例7:在梯形ABCD中,AD∥BC,AB=5,
AC=9,∠BCA=30°,∠ADB=45°,求
∠BAD的正弦值和BD的长.
分析:观察到BD为△BDC和△ABD的公共
边,由于△BDC中已知量较少,故考虑通过
解△ABD求出BD的长.
B
A
D
C
5
9
30°
45°
典型例题
例7:在梯形ABCD中,AD∥BC,AB=5,
AC=9,∠BCA=30°,∠ADB=45°,求
∠BAD的正弦值和BD的长.
分析:在△ABD中已知边AB的长及其所对
角∠ADB的度数,故只需要求出∠BAD的
正弦值,就可以利用正弦定理求出BD的长.
B
A
D
C
5
9
30°
45°
典型例题
例7:在梯形ABCD中,AD∥BC,AB=5,
AC=9,∠BCA=30°,∠ADB=45°,求
∠BAD的正弦值和BD的长.
分析:我们发现∠ABC与∠BAD互补,而
∠ABC所在的△ABC中已知两边及其中一
边的对角,可以由正弦定理求出∠ABC的
正弦值,再由∠BAD与
∠ABC互补的条件,求
出∠BAD的正弦值,进
而求出BD的长.
B
A
D
C
5
9
30°
45°
典型例题
例7:在梯形ABCD中,AD∥BC,AB=5,
AC=9,∠BCA=30°,∠ADB=45°,求
∠BAD的正弦值和BD的长.
解:在△ABC中,AB=5,AC=9,∠BCA=30°,由正弦定理,得
????????????????????∠????????????=????????????????????∠???????????? ,
?
sin∠ABC=????????????????????∠????????????????????
=????????????????????????°????=????????????.
?
B
A
D
C
5
9
30°
45°
典型例题
例7:在梯形ABCD中,AD∥BC,AB=5,
AC=9,∠BCA=30°,∠ADB=45°,求
∠BAD的正弦值和BD的长.
解:因为AD∥BC,
所以∠BAD=180°-∠ABC,
于是sin∠BAD=sin∠ABC=?????????????.
?
B
A
D
C
5
9
30°
45°
典型例题
例7:在梯形ABCD中,AD∥BC,AB=5,
AC=9,∠BCA=30°,∠ADB=45°,求
∠BAD的正弦值和BD的长.
解:在△ABD中,由正弦定理,得
????????????????????∠????????????=????????????????????∠???????????? ,
?
BD= ????????????????????∠????????????????????????∠????????????=????×?????????????????????= ??????????????.
?
B
A
D
C
5
9
30°
45°
典型例题
例8:如图,一次机器人足球比赛中,甲队4号
机器人由点A开始做匀速直线运动,到达点B
时,发现足球在点D处正以2倍于自己的速度
向点A做匀速直线滚动.已知AB=4???? dm,
AD=17 dm,∠BAD=45°.若忽略机器人原地
旋转所需的时间,则该机器人最快可在何处截
住足球?
?
D
A
B
45°
(1)
典型例题
例8:已知AB=4???? dm, AD=17 dm,∠BAD
=45°.若忽略机器人原地旋转所需的时间,则
该机器人最快可在何处截住足球?
?
解:机器人最快截住足球的地方是机器人与足
球同时到达的地方.如图(2),设该机器人最快
可在点C处截住足球,BC=x dm,由题意,
CD=2x dm,AC=AD-CD=(17-2x)dm.
D
A
B
C
45°
(2)
典型例题
解:在△ABC中,由余弦定理,得
BC2=AB2+AC2-2AB·ACcosA,
即x2=(4????)2+(17-2x)2-2×4????×(17-2x)cos45°,
解得x1=5,x2=????????????.
所以AC=7 dm,或AC=????????????? dm(不合题意,舍去).
?
例8:已知AB=4???? dm, AD=17 dm,∠BAD
=45°.若忽略机器人原地旋转所需的时间,则
该机器人最快可在何处截住足球?
?
D
A
B
C
45°
(2)
典型例题
解:因此,该机器人最快可在线段AD上离点A处7 dm的点C处藏住足球.
例8:已知AB=4???? dm, AD=17 dm,∠BAD
=45°.若忽略机器人原地旋转所需的时间,则
该机器人最快可在何处截住足球?
?
D
A
B
C
45°
(2)
典型例题
例9:已知△ABC的角A,B,C所对的边分别
是a,b,c,向量????= (a,b), ????= (sinB,sinA) ,
????= (b-c,a-c).
(1)若????∥ ????,求证: △ABC为等腰三角形;
(2)若????∥ ????, c=2, C=60°,求△ABC为的面
积.
?
典型例题
解: (1)因为 ????∥ ????,所以asinA=bsinB.
由正弦定理可得a·????????????=b·???????????? ,其中R是△ABC的
外接圆半径,所以a=b.即△ABC为等腰三角形.
?
例9:已知△ABC的角A,B,C所对的边分别
是a,b,c,向量????= (a,b), ????= (sinB,sinA) ,
????= (b-c,a-c).
(1)若????∥ ????,求证: △ABC为等腰三角形;
?
典型例题
解: (2)因为 ????⊥????,
所以(a,b)(b-c,a-c)=ab-ac+ab-bc=2ab-c(a+b)=0.
由c=2,得ab=a+b.①
由余弦定理可知,4=a2+b2-ab=(a+b) 2-3ab.②
?
例9:已知△ABC的角A,B,C所对的边分别
是a,b,c,向量????= (a,b), ????= (sinB,sinA) ,
????= (b-c,a-c).
(2)若????∥ ????, c=2, C=60°,求△ABC为的面
积.
?
典型例题
解: (2) 将①式代入②式,得(ab)2-3ab-4=0.
所以ab=4,或ab=-1(不合题意,舍去).
所以S△ABC=????????absinC=????????×4×sin60°= ????.
?
例9:已知△ABC的角A,B,C所对的边分别
是a,b,c,向量????= (a,b), ????= (sinB,sinA) ,
????= (b-c,a-c).
(2)若????∥ ????, c=2, C=60°,求△ABC为的面
积.
?
典型例题
例10:自动卸货汽车采用液压机构(如图).设计
时需要计算油泵顶杠BC的长度,已知车厢的最
大仰角为60°(指车厢AC与水平线之间的夹角).
油泵顶点B与车厢支点A之间的距离为1.95 m,
AB与水平线之间的夹角为6°20′,AC长为1.40
m.计算BC的长度.(精确到0.01 m)
典型例题
例10:已知车厢的最大仰角为60°(指车厢AC
与水平线之间的夹角).油泵顶点B与车厢支点A
之间的距离为1.95 m,AB与水平线之间的夹角
为6°20′,AC长为1.40 m.计算BC的长度.(精确
到0.01 m)
解:如图,在△ABC中,AB= 1.95 m,AC=1.40 m,∠BAC=60°+ 6°20′=66°20′.
60°
A
C
B
6°20′
典型例题
例10:已知车厢的最大仰角为60°(指车厢AC
与水平线之间的夹角).油泵顶点B与车厢支点A
之间的距离为1.95 m,AB与水平线之间的夹角
为6°20′,AC长为1.40 m.计算BC的长度.(精确
到0.01 m)
解:由余弦定理,得
BC2=AB2+AC2=2AB·ACcosA
=1.952+1.402-2×1.95×1.40cos66°20′
≈3.571.
60°
A
C
B
6°20′
典型例题
例10:已知车厢的最大仰角为60°(指车厢AC
与水平线之间的夹角).油泵顶点B与车厢支点A
之间的距离为1.95 m,AB与水平线之间的夹角
为6°20′,AC长为1.40 m.计算BC的长度.(精确
到0.01 m)
解:∴BC≈1.89 (m)
60°
A
C
B
6°20′
典型例题
例11:如图,C,D两点相距12 m,与烟囱底部
A在同一水平直线上,利用高为1.5 m的测角仪
器,测得烟囱在点C1,D1,的仰角分别是α=45°和β=60°.计算烟囱的高AB(精确到0.01 m).
典型例题
例11:如图,C,D两点相距12 m,与烟囱底部
A在同一水平直线上,利用高为1.5 m的侧角仪
器,测得烟囱在点C1,D1,的仰角分别是α=45°和β=60°.计算烟囱的高AB(精确到0.01 m).
解:如图,在△BC1D1中,
∠BD1C1=180°-60°=120°,
∠C1BD1=60°-45°=15°,
C1D1=CD=12.
典型例题
例11:如图,C,D两点相距12 m,与烟囱底部
A在同一水平直线上,利用高为1.5 m的侧角仪
器,测得烟囱在点C1,D1,的仰角分别是α=45°和β=60°.计算烟囱的高AB(精确到0.01 m).
解:由正弦定理,得????????????????????????????∠????????????????????=????????????????????????∠????????????????????,
????????????=????????????????????????????∠????????????????????????????????∠????????????????????
=????????????????????????????????°????????????????????°≈40.153(m),
?
典型例题
例11:如图,C,D两点相距12 m,与烟囱底部
A在同一水平直线上,利用高为1.5 m的侧角仪
器,测得烟囱在点C1,D1,的仰角分别是α=45°和β=60°.计算烟囱的高AB(精确到0.01 m).
解:从而????????????= ???????? ???????????? ≈28.392(m).
AB= ????????????+A????????=????????.????????????+1.5=29.892
≈29.89(m).
因此,烟囱的高为29.89 m.
?
典型例题
例12:如图(1),直线a表示海面上一条南北方向的海
防警戒线,在a上点A处有一个水声监测点,另两个
监测点B,C分别在点A的正东方20 km处和54 km处.
某时刻,监侧点B收到发自静止目标P的一个声波,
监测点A,C分别在8 s和20 s后相继收到这一信号.在
当时的气象条件下,声波在水中的传播速度是1.5
km/s.
(1)设PA=x km,用x分别表示PB,PC,并求x的值;
(2)求静止目标P到海防 警戒线a的距离.(精确到0.01
km)
(1)
A
B
C
P
a
东
北
典型例题
例12:如图(1),在a上点A处有一个水声监测点,另两
个监测点B,C分别在点A的正东方20 km处和54 km
处.某时刻,监侧点B收到发自静止目标P的一个声波,
监测点A,C分别在8 s和20 s后相继收到这一信号.在
当时的气象条件下,声波在水中的传播速度是1.5 km/s.
(1)设PA=x km,用x分别表示PB,PC,并求x的值;
解:(1)依题意,PA- PB=1.5×8=12(km),
PC-PB=1.5×20=30(km),
因此PB=(x-12)km,PC=(18+x)km.
(1)
A
B
C
P
a
东
北
典型例题
例12:如图(1),在a上点A处有一个水声监测点,另两
个监测点B,C分别在点A的正东方20 km处和54 km
处.某时刻,监侧点B收到发自静止目标P的一个声波,
监测点A,C分别在8 s和20 s后相继收到这一信号.在
当时的气象条件下,声波在水中的传播速度是1.5 km/s.
(1)设PA=x km,用x分别表示PB,PC,并求x的值;
解:(1) 在△PAB中,AB=20 km,
cos∠PAB=????????????+?????????????????????????????????????·????????
?
=????????+?????????????(??????????????)????????????·????????
?
=????????+????????????????.
?
(1)
A
B
C
P
a
东
北
典型例题
例12:如图(1),在a上点A处有一个水声监测点,另两
个监测点B,C分别在点A的正东方20 km处和54 km
处.某时刻,监侧点B收到发自静止目标P的一个声波,
监测点A,C分别在8 s和20 s后相继收到这一信号.在
当时的气象条件下,声波在水中的传播速度是1.5 km/s.
(1)设PA=x km,用x分别表示PB,PC,并求x的值;
解:(1) 同理cos∠PAC=?????????????????????,
?
得????????+????????????????=?????????????????????,
?
由cos∠PAB=cos∠PAC,
解得x=?????????????????.
?
(1)
A
B
C
P
a
东
北
典型例题
例12:如图(1),在a上点A处有一个水声监测点,另两
个监测点B,C分别在点A的正东方20 km处和54 km
处.某时刻,监侧点B收到发自静止目标P的一个声波,
监测点A,C分别在8 s和20 s后相继收到这一信号.在
当时的气象条件下,声波在水中的传播速度是1.5 km/s.
(2)求静止目标P到海防警戒线a的距离.(精确到0.01
km)
解:(1) 如图(2),过点P作a的垂线,垂足为D,在
Rt△PDA中,
PD=PAcos∠APD=PAcos∠PAB
=x· ????????+????????????????,
?
(2)
A
B
C
P
a
东
北
典型例题
例12:如图(1),在a上点A处有一个水声监测点,另两
个监测点B,C分别在点A的正东方20 km处和54 km
处.某时刻,监侧点B收到发自静止目标P的一个声波,
监测点A,C分别在8 s和20 s后相继收到这一信号.在
当时的气象条件下,声波在水中的传播速度是1.5 km/s.
(2)求静止目标P到海防警戒线a的距离.(精确到0.01
km)
解:(2) 所以PD=????×????????????????+?????????????= ????????????????≈17.71 (km).
?
因此,静止目标P到海防警戒
线a的距离约为17.71 km.
(2)
A
B
C
P
a
东
北
综合练习
在△ABC中,cosC= ?????????,AC=4,BC=3,则sinB=______.
?
解:在△ABC中,cosC= ????????,AC=4,BC=3,
由余弦定理可得AB2=AC2+BC2-2AC·BCcosC=42+32-
2×4×3× ????????=9,故AB=3.
cosB=????????????+?????????????????????????????????????·????????=????????+?????????????????????×????×????=????????,
可得sinB=??????????????????????????=????????????.
?
????????????
?
综合练习
在四边形ABCD中,AB∥CD,AD=BD=CD=1.
(1)若AB= ?????????,求BC;
(2)若AB=2BC,求cos∠BDC.
?
解: (1)cos∠ABD=????????????+?????????????????????????????????????·????????=(????????)????+?????????????????????×????????×????=????????,
由AB∥CD,
所以∠BDC=∠ABD,
即cos∠BDC=cos∠ABD=????????,
?
综合练习
在四边形ABCD中,AB∥CD,AD=BD=CD=1.
(1)若AB= ?????????,求BC;
(2)若AB=2BC,求cos∠BDC.
?
解: (1)所以????????????=????????????+????????????- ????????????·????????????????????∠????????????=
=12+12-2×1×1× ????????=????????.
所以BC=????????.
?
综合练习
在四边形ABCD中,AB∥CD,AD=BD=CD=1.
(1)若AB= ?????????,求BC;
(2)若AB=2BC,求cos∠BDC.
?
解: (2)设BC=x,则AB=2BC=2x,
由余弦定理得:
cos∠ADB=????????????+?????????????????????????????????????·????????=(????????)????+?????????????????????×????????×????=x,
cos∠BDC=????????????+?????????????????????????????????????·????????=????????+?????????????????????×????×????=?????????????????,
故?????????????????=x,解得x=????-1或?????--1(舍去).
cos∠BDC= ????--1.
?
本课小结
再 见
授课教师:
温故知新
学习目标
1.通过对特殊三角形边角间数量关系的研究,发
现余弦定理与正弦定理,并了解其向量证法;(难点)
2.掌握余弦定理与正弦定理,并能运用其解三角
形.(重点)
课文精讲
问题提出
三角形中边角关系很丰富,本节继续研究.
如已知两边及其夹角,怎么求出此角的对边呢?
已知三条边,又怎么求出它的三个角呢?
余弦定理
课文精讲
分析理解
我们利用向量来研究.
如图,在△ABC中,设|????????|=a,|????????|=b,
|????????|=c,根据向量的数量积,可得
?
余弦定理
a2= ????????· ????????=(????????-????????)·(????????-????????)
=|????????|2-2|????????|·|????????|cosA+|????????|2
=b2-2bccosA+c2,
即a2= b2+c2-2bccosA.
?
A
B
C
a
c
b
课文精讲
余弦定理 三角形任何一边的平方等于其他
两边的平方和减去这两边与它们
夹角余弦的积的两倍,即
余弦定理
a2=b2+c2-2bccosA
b2=a2+c2-2accosB
c2=a2+b2-2abcosC
课文精讲
利用余弦定理,可以由三角形的三条边,
求出它三个角的大小.
余弦定理
典型例题
例1:如图,有两条直线AB和CD相交成80°
角,交点是O.甲、乙两人同时从点O分别沿
OA,OC方向出发,速度分别是4 km/h,4. 5
km/h. 3 h后两人相距多远?(精确到0.1km)
解:经过3 h,甲到达点P,|OP|=4×3=12(km),
乙到达点Q,|OQ|=4.5×3=13.5(km).
A
C
O
B
D
P
Q
80°
典型例题
例1:如图,有两条直线AB和CD相交成80°
角,交点是O.甲、乙两人同时从点O分别沿
OA,OC方向出发,速度分别是4 km/h,4. 5
km/h. 3 h后两人相距多远?(精确到0.1km)
解:在△OPQ中,依余弦定理,得
|PQ|=????????????+|????????|?????????|????????||????????|?????????????∠????????????
=????????????+????????.?????????????×????????×????????.?????????????????????????°≈16.4(km).
?
A
C
O
B
D
P
Q
80°
典型例题
例1:如图,有两条直线AB和CD相交成80°
角,交点是O.甲、乙两人同时从点O分别沿
OA,OC方向出发,速度分别是4 km/h,4. 5
km/h. 3 h后两人相距多远?(精确到0.1km)
解:因此,3 h后两人相距约16.4 km.
A
C
O
B
D
P
Q
80°
典型例题
解:在△BCD中,BC=1,CD=1,∠BCD=135°,
BD2=BC2+CD2-2BC·CDcos∠BCD
12+12-2×1×1cos135°=2+????.
所以BD≈1.8.
?
例2:如图是古希腊数学家特埃特图斯用来构
造无理数????, ?????, ?????,···的图形.试计算图
中线段BD的长度及∠DAB的大小.(长度精确到
0.1,角度精确到1°)
?
A
B
C
D
1
1
1
????
?
????
?
典型例题
解:在△ABD中,AB=1,BD=????+????,AD=????,
cos∠DAB=????????+(????)?????(????+????)????×????×????
=??????????????????≈0.1691.
?
例2:如图是古希腊数学家特埃特图斯用来构
造无理数????, ?????, ?????,···的图形.试计算图
中线段BD的长度及∠DAB的大小.(长度精确到
0.1,角度精确到1°)
?
所以∠DAB≈80°.
A
B
C
D
1
1
1
????
?
????
?
典型例题
解:由A是锐角,且cos2A=-????????,得2A=????????????,A=????????.
?
例3:在△ABC中,a,b,c分别是角A,B,C
的对边,已知A是锐角,且cos2A=-????????.
(1)若mbc=b2+c2-a2,求实数m的值;
(2)若a=????,求△ABC面积的最大值.
?
(1) mbc=b2+c2-a2,可变形为????????+?????????????????????????????=????????.
依据余弦定理,可知cosA=????????+?????????????????????????????=????????,????????=????????,所以m=1.
?
典型例题
解:
例3:在△ABC中,a,b,c分别是角A,B,C
的对边,已知A是锐角,且cos2A=-????????.
(1)若mbc=b2+c2-a2,求实数m的值;
(2)若a=????,求△ABC面积的最大值.
?
(2) 因为sinA=sin????????=????????,
所以bc= b2+c2-a2≥2bc-a2,
即bc≤a2.故S △ABC=????????????sinA
≤ ?????????????· ????????=????????????.
?
S △ABC=???????? ch=????????cbsinA
?
A
B
C
c
b
h
典型例题
解:(2)即所求△ABC面积的最大值是????????????.
?
例3:在△ABC中,a,b,c分别是角A,B,C
的对边,已知A是锐角,且cos2A=-????????.
(1)若mbc=b2+c2-a2,求实数m的值;
(2)若a=????,求△ABC面积的最大值.
?
S △ABC=???????? ch=????????cbsinA
?
A
B
C
c
b
h
课文精讲
问题提出
如图,若△ABC是直角三角形,C=90°,
则由sinA=-????????,sinB=-????????,
可知 ????????????????????=????????????????????=c.
因为C=90°,sinC=1,
所以????????????????????=????????????????????=????????????????????.
?
正弦定理
C
B
A
b
c
a
课文精讲
对等边三角形,这个等式无疑也成立;对
其他三角形,它是否仍然成立呢?
正弦定理
C
B
A
b
c
a
课文精讲
分析理解
如图,△ABC是锐角三角形,CD是边AB
上的高,根据三角函数的定义,
CD=asinB,
CD=bsinA,
所以????????????????????=????????????????????.
?
正弦定理
B
A
C
D
a
b
课文精讲
分析理解
同理 ????????????????????=????????????????????.
即????????????????????=????????????????????=????????????????????.
?
正弦定理
因此,对锐角三角形,以上等式仍然成立.
B
A
C
D
a
b
课文精讲
探究:当△ABC是钝角三角形时,以上等式是
否仍然成立?
正弦定理
成立
课文精讲
正弦定理 在一个三角形中,各边和它所对
角的正弦的比相等,即
正弦定理
????????????????????=????????????????????=????????????????????
?
运用由特殊到一般的方法发现了正弦定理,
这种思想方法经常用于发现客观规律.
典型例题
例4:某地出土一块古代玉佩(如图),其一角
已破损,现测得如下数据:BC=2.57 cm,
CE=3. 57 cm,BD=4.38 cm,B=450,
C=120°.为了复原,请计算原玉佩另两边的
长.(精确到0. 01 cm)
D
E
B
C
典型例题
例4:某地出土一块古代玉佩(如图),其一角
已破损,现测得如下数据:BC=2.57 cm,
CE=3. 57 cm,BD=4.38 cm,B=45°,
C=120°.为了复原,请计算原玉佩另两边的
长.(精确到0. 01 cm)
解:将BD,CE分别延长
相交于点A(如图),
在△ABC中,BC=2.57 cm,
B=45°,C=120°,
A=180°-(B+C)=180°- (45°+120°)=15°.
D
E
B
C
A
典型例题
例4:某地出土一块古代玉佩(如图),其一角
已破损,现测得如下数据:BC=2.57 cm,
CE=3. 57 cm,BD=4.38 cm,B=45°,
C=120°.为了复原,请计算原玉佩另两边的
长.(精确到0. 01 cm)
解:由正弦定理,得
????????????????????????=???????????????????????? ,
?
所以
AC=????????????????????????????????????????=????.????????????????????????????°????????????????????° ≈7.02(cm),
?
D
E
B
C
A
典型例题
例4:某地出土一块古代玉佩(如图),其一角
已破损,现测得如下数据:BC=2.57 cm,
CE=3. 57 cm,BD=4.38 cm,B=45°,
C=120°.为了复原,请计算原玉佩另两边的
长.(精确到0. 01 cm)
解:同理AB≈8.60(cm).
因此,原玉佩另两边的长
分别约为7.02 cm,8.60 cm.
D
E
B
C
A
典型例题
例5:求证:如图(1),以Rt△ABC斜边AB为
直径作外接圆,设这个外接圆的半径为R,则
????????????????????=????????????????????=????????????????????=2R.
?
证明:在Rt△ABC中,C=90°,????????????????????=c,
又????????????????????=????????????????????=????????????????????,且c=2R,
所以????????????????????=????????????????????=????????????????????=2R.
?
(1)
C
B
A
·
课文精讲
思考
对于钝角三角形(如图(2))、锐角三角形
(如图(3)),上述结论还成立吗?
(2)
B
B
A
·
C
(3)
B
A
·
C
B′
B′
成立
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:如图,设台风中心从点B向西北方向沿射
线BD移动,该市位于点B正西
方向300 km处的点A.
D
A
B
北
东
C
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:假设经过t h,台风中心到达点C.在△ABC
中,AB=300 km, AC=250 km,
BC=40t km,B=45°.
D
A
B
北
东
C
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:由正弦定理,得????????????????????????=????????????????????????=????????????????????????,
????????????????=?????????????????????????????????=????????????????????????????????°????????????
≈0.8485.
?
D
A
B
北
东
C
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:所以角C有两个解(如图①):
∠AC1B≈121.95°,
∠AC2B≈58.05°.
图①
D
A
B
北
东
C2
C1
E
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:当∠AC1B≈121.95°时,
∠C1AB=180°-(B+∠ AC1B)
≈180°-(45°+121.95°)
=13.05°.
图①
D
A
B
北
东
C2
C1
E
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:从而BC1=????????????????????????????????????????????
=????????????????????????????????.????????°????????????????????°
=250????sin13.05°(km),
?
图①
D
A
B
北
东
C2
C1
E
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:t1=?????????????????????=????????????????????????????????????.????????°????????
≈2.00?(h).
?
图①
D
A
B
北
东
C2
C1
E
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:同理,当∠AC2B≈58.05°时,
BC2=250????sin76.95° km,
t2 ≈8.61 h.
t2 - t1 ≈8.61-2.00≈6.6(h).
?
图①
D
A
B
北
东
C2
C1
E
典型例题
例6:台风中心位于某市正东方向300 km处,
正以40 km/h的速度向西北方向移动,距离台
风中心250 km范围内将会受其影响.如果台风
风速不变,那么该市从何时起要遭受台风影响?
这种影响持续多长时间?(精确到0. 1 h)
解:因此,约2h后将要遭受台风影
响,持续约6.6 h.
图①
D
A
B
北
东
C2
C1
E
谢 谢
课文精讲
思考:
已知两条边的边长和其中一条边的对角的大小解三角形,它的解有几种情况?
课文精讲
正弦定理、余弦定理是两个重要定理,在
解决与三角形有关的几何计算问题中有着广泛的应用.
用正弦定理、余弦定理解三角形
在三角形的三条边和三个角这6个元素中,
如果已知3个(至少含一边长),那么由余弦定
理和正弦定理,就可以求得其他3个元素.具体
情形如下:
课文精讲
情形1:已知两个角的大小和一条边的边长.
先由三角形内角和等于180°求出第三个
角的大小,然后依据正弦定理求得另外两条
的边长.
用正弦定理、余弦定理解三角形
情形2:已知两条边的边长及其夹角的大小.
先由余弦定理求出第三条边的边长,然
后再由余弦定理求得第二、第三个角的大小.
课文精讲
情形3:已知三条边的边长.
由余弦定理求出两个角,再利用三角形内
角和等于180°求出第三个角.
用正弦定理、余弦定理解三角形
课文精讲
用正弦定理、余弦定理解三角形
情形4:已知两条边的边长和其中一边对角的
大小.
首先,由正弦定理求出第二条边所对角的
正弦,这时,要判断是两解、一解还是无解.
然后,根据三角形内角和等于180°得到第三个
角的大小.最后,由余弦定理或正弦定理求得第三条边的边长.
典型例题
例7:在梯形ABCD中,AD∥BC,AB=5,
AC=9,∠BCA=30°,∠ADB=45°,求
∠BAD的正弦值和BD的长.
分析:观察到BD为△BDC和△ABD的公共
边,由于△BDC中已知量较少,故考虑通过
解△ABD求出BD的长.
B
A
D
C
5
9
30°
45°
典型例题
例7:在梯形ABCD中,AD∥BC,AB=5,
AC=9,∠BCA=30°,∠ADB=45°,求
∠BAD的正弦值和BD的长.
分析:在△ABD中已知边AB的长及其所对
角∠ADB的度数,故只需要求出∠BAD的
正弦值,就可以利用正弦定理求出BD的长.
B
A
D
C
5
9
30°
45°
典型例题
例7:在梯形ABCD中,AD∥BC,AB=5,
AC=9,∠BCA=30°,∠ADB=45°,求
∠BAD的正弦值和BD的长.
分析:我们发现∠ABC与∠BAD互补,而
∠ABC所在的△ABC中已知两边及其中一
边的对角,可以由正弦定理求出∠ABC的
正弦值,再由∠BAD与
∠ABC互补的条件,求
出∠BAD的正弦值,进
而求出BD的长.
B
A
D
C
5
9
30°
45°
典型例题
例7:在梯形ABCD中,AD∥BC,AB=5,
AC=9,∠BCA=30°,∠ADB=45°,求
∠BAD的正弦值和BD的长.
解:在△ABC中,AB=5,AC=9,∠BCA=30°,由正弦定理,得
????????????????????∠????????????=????????????????????∠???????????? ,
?
sin∠ABC=????????????????????∠????????????????????
=????????????????????????°????=????????????.
?
B
A
D
C
5
9
30°
45°
典型例题
例7:在梯形ABCD中,AD∥BC,AB=5,
AC=9,∠BCA=30°,∠ADB=45°,求
∠BAD的正弦值和BD的长.
解:因为AD∥BC,
所以∠BAD=180°-∠ABC,
于是sin∠BAD=sin∠ABC=?????????????.
?
B
A
D
C
5
9
30°
45°
典型例题
例7:在梯形ABCD中,AD∥BC,AB=5,
AC=9,∠BCA=30°,∠ADB=45°,求
∠BAD的正弦值和BD的长.
解:在△ABD中,由正弦定理,得
????????????????????∠????????????=????????????????????∠???????????? ,
?
BD= ????????????????????∠????????????????????????∠????????????=????×?????????????????????= ??????????????.
?
B
A
D
C
5
9
30°
45°
典型例题
例8:如图,一次机器人足球比赛中,甲队4号
机器人由点A开始做匀速直线运动,到达点B
时,发现足球在点D处正以2倍于自己的速度
向点A做匀速直线滚动.已知AB=4???? dm,
AD=17 dm,∠BAD=45°.若忽略机器人原地
旋转所需的时间,则该机器人最快可在何处截
住足球?
?
D
A
B
45°
(1)
典型例题
例8:已知AB=4???? dm, AD=17 dm,∠BAD
=45°.若忽略机器人原地旋转所需的时间,则
该机器人最快可在何处截住足球?
?
解:机器人最快截住足球的地方是机器人与足
球同时到达的地方.如图(2),设该机器人最快
可在点C处截住足球,BC=x dm,由题意,
CD=2x dm,AC=AD-CD=(17-2x)dm.
D
A
B
C
45°
(2)
典型例题
解:在△ABC中,由余弦定理,得
BC2=AB2+AC2-2AB·ACcosA,
即x2=(4????)2+(17-2x)2-2×4????×(17-2x)cos45°,
解得x1=5,x2=????????????.
所以AC=7 dm,或AC=????????????? dm(不合题意,舍去).
?
例8:已知AB=4???? dm, AD=17 dm,∠BAD
=45°.若忽略机器人原地旋转所需的时间,则
该机器人最快可在何处截住足球?
?
D
A
B
C
45°
(2)
典型例题
解:因此,该机器人最快可在线段AD上离点A处7 dm的点C处藏住足球.
例8:已知AB=4???? dm, AD=17 dm,∠BAD
=45°.若忽略机器人原地旋转所需的时间,则
该机器人最快可在何处截住足球?
?
D
A
B
C
45°
(2)
典型例题
例9:已知△ABC的角A,B,C所对的边分别
是a,b,c,向量????= (a,b), ????= (sinB,sinA) ,
????= (b-c,a-c).
(1)若????∥ ????,求证: △ABC为等腰三角形;
(2)若????∥ ????, c=2, C=60°,求△ABC为的面
积.
?
典型例题
解: (1)因为 ????∥ ????,所以asinA=bsinB.
由正弦定理可得a·????????????=b·???????????? ,其中R是△ABC的
外接圆半径,所以a=b.即△ABC为等腰三角形.
?
例9:已知△ABC的角A,B,C所对的边分别
是a,b,c,向量????= (a,b), ????= (sinB,sinA) ,
????= (b-c,a-c).
(1)若????∥ ????,求证: △ABC为等腰三角形;
?
典型例题
解: (2)因为 ????⊥????,
所以(a,b)(b-c,a-c)=ab-ac+ab-bc=2ab-c(a+b)=0.
由c=2,得ab=a+b.①
由余弦定理可知,4=a2+b2-ab=(a+b) 2-3ab.②
?
例9:已知△ABC的角A,B,C所对的边分别
是a,b,c,向量????= (a,b), ????= (sinB,sinA) ,
????= (b-c,a-c).
(2)若????∥ ????, c=2, C=60°,求△ABC为的面
积.
?
典型例题
解: (2) 将①式代入②式,得(ab)2-3ab-4=0.
所以ab=4,或ab=-1(不合题意,舍去).
所以S△ABC=????????absinC=????????×4×sin60°= ????.
?
例9:已知△ABC的角A,B,C所对的边分别
是a,b,c,向量????= (a,b), ????= (sinB,sinA) ,
????= (b-c,a-c).
(2)若????∥ ????, c=2, C=60°,求△ABC为的面
积.
?
典型例题
例10:自动卸货汽车采用液压机构(如图).设计
时需要计算油泵顶杠BC的长度,已知车厢的最
大仰角为60°(指车厢AC与水平线之间的夹角).
油泵顶点B与车厢支点A之间的距离为1.95 m,
AB与水平线之间的夹角为6°20′,AC长为1.40
m.计算BC的长度.(精确到0.01 m)
典型例题
例10:已知车厢的最大仰角为60°(指车厢AC
与水平线之间的夹角).油泵顶点B与车厢支点A
之间的距离为1.95 m,AB与水平线之间的夹角
为6°20′,AC长为1.40 m.计算BC的长度.(精确
到0.01 m)
解:如图,在△ABC中,AB= 1.95 m,AC=1.40 m,∠BAC=60°+ 6°20′=66°20′.
60°
A
C
B
6°20′
典型例题
例10:已知车厢的最大仰角为60°(指车厢AC
与水平线之间的夹角).油泵顶点B与车厢支点A
之间的距离为1.95 m,AB与水平线之间的夹角
为6°20′,AC长为1.40 m.计算BC的长度.(精确
到0.01 m)
解:由余弦定理,得
BC2=AB2+AC2=2AB·ACcosA
=1.952+1.402-2×1.95×1.40cos66°20′
≈3.571.
60°
A
C
B
6°20′
典型例题
例10:已知车厢的最大仰角为60°(指车厢AC
与水平线之间的夹角).油泵顶点B与车厢支点A
之间的距离为1.95 m,AB与水平线之间的夹角
为6°20′,AC长为1.40 m.计算BC的长度.(精确
到0.01 m)
解:∴BC≈1.89 (m)
60°
A
C
B
6°20′
典型例题
例11:如图,C,D两点相距12 m,与烟囱底部
A在同一水平直线上,利用高为1.5 m的测角仪
器,测得烟囱在点C1,D1,的仰角分别是α=45°和β=60°.计算烟囱的高AB(精确到0.01 m).
典型例题
例11:如图,C,D两点相距12 m,与烟囱底部
A在同一水平直线上,利用高为1.5 m的侧角仪
器,测得烟囱在点C1,D1,的仰角分别是α=45°和β=60°.计算烟囱的高AB(精确到0.01 m).
解:如图,在△BC1D1中,
∠BD1C1=180°-60°=120°,
∠C1BD1=60°-45°=15°,
C1D1=CD=12.
典型例题
例11:如图,C,D两点相距12 m,与烟囱底部
A在同一水平直线上,利用高为1.5 m的侧角仪
器,测得烟囱在点C1,D1,的仰角分别是α=45°和β=60°.计算烟囱的高AB(精确到0.01 m).
解:由正弦定理,得????????????????????????????∠????????????????????=????????????????????????∠????????????????????,
????????????=????????????????????????????∠????????????????????????????????∠????????????????????
=????????????????????????????????°????????????????????°≈40.153(m),
?
典型例题
例11:如图,C,D两点相距12 m,与烟囱底部
A在同一水平直线上,利用高为1.5 m的侧角仪
器,测得烟囱在点C1,D1,的仰角分别是α=45°和β=60°.计算烟囱的高AB(精确到0.01 m).
解:从而????????????= ???????? ???????????? ≈28.392(m).
AB= ????????????+A????????=????????.????????????+1.5=29.892
≈29.89(m).
因此,烟囱的高为29.89 m.
?
典型例题
例12:如图(1),直线a表示海面上一条南北方向的海
防警戒线,在a上点A处有一个水声监测点,另两个
监测点B,C分别在点A的正东方20 km处和54 km处.
某时刻,监侧点B收到发自静止目标P的一个声波,
监测点A,C分别在8 s和20 s后相继收到这一信号.在
当时的气象条件下,声波在水中的传播速度是1.5
km/s.
(1)设PA=x km,用x分别表示PB,PC,并求x的值;
(2)求静止目标P到海防 警戒线a的距离.(精确到0.01
km)
(1)
A
B
C
P
a
东
北
典型例题
例12:如图(1),在a上点A处有一个水声监测点,另两
个监测点B,C分别在点A的正东方20 km处和54 km
处.某时刻,监侧点B收到发自静止目标P的一个声波,
监测点A,C分别在8 s和20 s后相继收到这一信号.在
当时的气象条件下,声波在水中的传播速度是1.5 km/s.
(1)设PA=x km,用x分别表示PB,PC,并求x的值;
解:(1)依题意,PA- PB=1.5×8=12(km),
PC-PB=1.5×20=30(km),
因此PB=(x-12)km,PC=(18+x)km.
(1)
A
B
C
P
a
东
北
典型例题
例12:如图(1),在a上点A处有一个水声监测点,另两
个监测点B,C分别在点A的正东方20 km处和54 km
处.某时刻,监侧点B收到发自静止目标P的一个声波,
监测点A,C分别在8 s和20 s后相继收到这一信号.在
当时的气象条件下,声波在水中的传播速度是1.5 km/s.
(1)设PA=x km,用x分别表示PB,PC,并求x的值;
解:(1) 在△PAB中,AB=20 km,
cos∠PAB=????????????+?????????????????????????????????????·????????
?
=????????+?????????????(??????????????)????????????·????????
?
=????????+????????????????.
?
(1)
A
B
C
P
a
东
北
典型例题
例12:如图(1),在a上点A处有一个水声监测点,另两
个监测点B,C分别在点A的正东方20 km处和54 km
处.某时刻,监侧点B收到发自静止目标P的一个声波,
监测点A,C分别在8 s和20 s后相继收到这一信号.在
当时的气象条件下,声波在水中的传播速度是1.5 km/s.
(1)设PA=x km,用x分别表示PB,PC,并求x的值;
解:(1) 同理cos∠PAC=?????????????????????,
?
得????????+????????????????=?????????????????????,
?
由cos∠PAB=cos∠PAC,
解得x=?????????????????.
?
(1)
A
B
C
P
a
东
北
典型例题
例12:如图(1),在a上点A处有一个水声监测点,另两
个监测点B,C分别在点A的正东方20 km处和54 km
处.某时刻,监侧点B收到发自静止目标P的一个声波,
监测点A,C分别在8 s和20 s后相继收到这一信号.在
当时的气象条件下,声波在水中的传播速度是1.5 km/s.
(2)求静止目标P到海防警戒线a的距离.(精确到0.01
km)
解:(1) 如图(2),过点P作a的垂线,垂足为D,在
Rt△PDA中,
PD=PAcos∠APD=PAcos∠PAB
=x· ????????+????????????????,
?
(2)
A
B
C
P
a
东
北
典型例题
例12:如图(1),在a上点A处有一个水声监测点,另两
个监测点B,C分别在点A的正东方20 km处和54 km
处.某时刻,监侧点B收到发自静止目标P的一个声波,
监测点A,C分别在8 s和20 s后相继收到这一信号.在
当时的气象条件下,声波在水中的传播速度是1.5 km/s.
(2)求静止目标P到海防警戒线a的距离.(精确到0.01
km)
解:(2) 所以PD=????×????????????????+?????????????= ????????????????≈17.71 (km).
?
因此,静止目标P到海防警戒
线a的距离约为17.71 km.
(2)
A
B
C
P
a
东
北
综合练习
在△ABC中,cosC= ?????????,AC=4,BC=3,则sinB=______.
?
解:在△ABC中,cosC= ????????,AC=4,BC=3,
由余弦定理可得AB2=AC2+BC2-2AC·BCcosC=42+32-
2×4×3× ????????=9,故AB=3.
cosB=????????????+?????????????????????????????????????·????????=????????+?????????????????????×????×????=????????,
可得sinB=??????????????????????????=????????????.
?
????????????
?
综合练习
在四边形ABCD中,AB∥CD,AD=BD=CD=1.
(1)若AB= ?????????,求BC;
(2)若AB=2BC,求cos∠BDC.
?
解: (1)cos∠ABD=????????????+?????????????????????????????????????·????????=(????????)????+?????????????????????×????????×????=????????,
由AB∥CD,
所以∠BDC=∠ABD,
即cos∠BDC=cos∠ABD=????????,
?
综合练习
在四边形ABCD中,AB∥CD,AD=BD=CD=1.
(1)若AB= ?????????,求BC;
(2)若AB=2BC,求cos∠BDC.
?
解: (1)所以????????????=????????????+????????????- ????????????·????????????????????∠????????????=
=12+12-2×1×1× ????????=????????.
所以BC=????????.
?
综合练习
在四边形ABCD中,AB∥CD,AD=BD=CD=1.
(1)若AB= ?????????,求BC;
(2)若AB=2BC,求cos∠BDC.
?
解: (2)设BC=x,则AB=2BC=2x,
由余弦定理得:
cos∠ADB=????????????+?????????????????????????????????????·????????=(????????)????+?????????????????????×????????×????=x,
cos∠BDC=????????????+?????????????????????????????????????·????????=????????+?????????????????????×????×????=?????????????????,
故?????????????????=x,解得x=????-1或?????--1(舍去).
cos∠BDC= ????--1.
?
本课小结
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
