北师大版七下 4.2 图形的全等 课件(17张)
文档属性
| 名称 | 北师大版七下 4.2 图形的全等 课件(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 353.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 13:55:35 | ||
图片预览





文档简介
图形的全等
1、知道全等图形,全等多边形,全等三角形的概念和性质
2、能找出全等多边形、全等三角形的对应元素、会利用图形的全等解决一些简单的问题
学习目标
重点
学习重点和难点
难点
应用全等图形的性质解决实际问题
寻找全等多边形的对应边、对应角;探究全等图形的性质
情境引入
找出右图中一对完全相同的的图形,并指出其与另一副图不同之处。
(1)
(2)
(3)
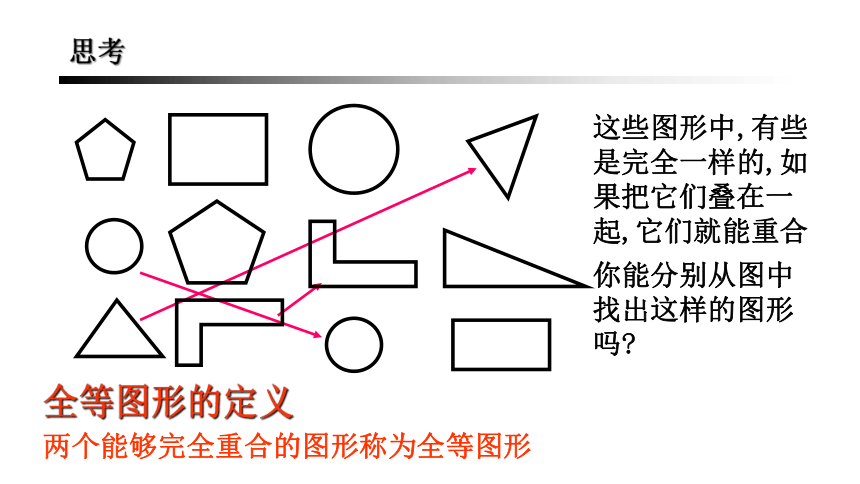
思考
全等图形的定义
这些图形中,有些是完全一样的,如果把它们叠在一起,它们就能重合
你能分别从图中找出这样的图形吗?
两个能够完全重合的图形称为全等图形
全等图形的判断
图中共有多少对全等图形,他们分别是
(1)
(2)
(3)
(4)
(5)
(10)
(7)
(8)
(9)
(14)
判定两个图形是否全等的基本方法是把他们重叠起来,看看他们是否能够互相重合,但在不少情况下, 无须把两个图形重叠在一起, 就知他们是否全等.
(6)
(11)
(12)
(13)
(15)
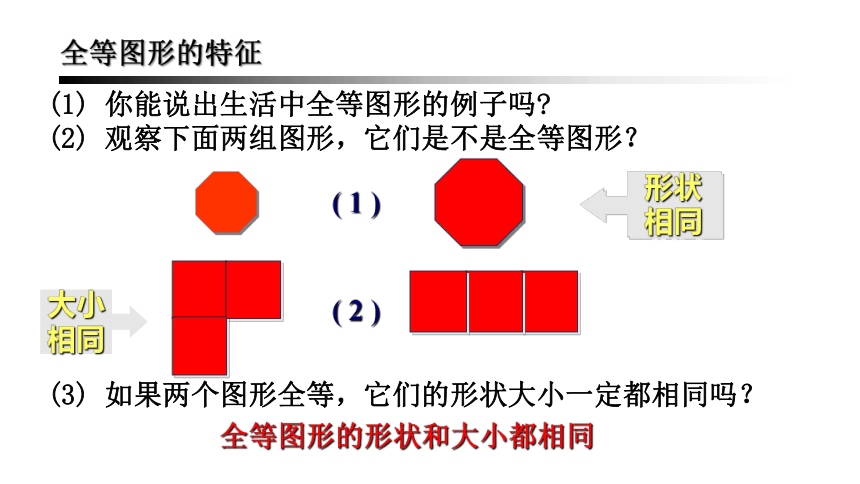
全等图形的特征
形状
相同
大小
相同
(1) 你能说出生活中全等图形的例子吗?
(2) 观察下面两组图形,它们是不是全等图形?
( 1 )
( 2 )
(3) 如果两个图形全等,它们的形状大小一定都相同吗?
全等图形的形状和大小都相同
观察图中的全等三角形应怎样表示?
注:记全等三角形时,通常把表示对应
顶点的字母写在对应的位置上.
△ ABC ≌△ DEF
全等三角形的性质
全等三角形的对应边相等,对应角相等.
(全等三角形的对应边相等)
(全等三角形的对应角相等)
∵△ABC≌ △A‘B’C‘
∴ AB=A’B‘, BC=B’C‘, AC=A’C‘
∴ ∠ A= ∠ A’, ∠ B= ∠B‘ ,
∠ C= ∠C’
图1中的全等的图形有( )
A 2组 B 3组
C 4组 D 5组
练习
B
练习
如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,
则BC=_____cm,∠B=_____.
B
A
E
F
C
3
64°
你还能求出哪些边的长度,
哪些角的度数?
下列各组图形是全等图形的是( )
B
练习
练习
如图,已知△ABC≌△DCB,且AB=DC,指出对应角和另外两组对边。
A
D
O
B
C
解:对应角为∠A和∠D,∠ABC和∠DCB,∠ACB和∠DBC,对应边还有AC和DB,BC和CB。
课堂小结
1、全等图形的概念
全等图形:能够 的两个图形称为全等图形
2、全等图形的特征
特征:全等图形的 和 都相同。
说明:(1)若事先知道两个全等图形,可得到它们的大小相同,即知道其中一个图形的面积可以求出另一个图形的面积。(2)全等图形的特征可作为判断两个图形全等的依据,先看它们的形状是否相同,再看大小是否相等。
大小
完全重合
形状
3、全等三角形
定义:能够完全重合的两个 叫做全等三角形。
对应顶点:能够重合的顶点。
对应边:能够重合的边。
对应角:能够重合的角。
4、全等三角形的性质
性质:全等三角形的对应边相等,对应角相等。
记法:用“≌” 表示,读作 “全等于”
注意:要把表示对应点的字母写在对应的位置上。
课堂小结
三角形
图片欣赏
1、知道全等图形,全等多边形,全等三角形的概念和性质
2、能找出全等多边形、全等三角形的对应元素、会利用图形的全等解决一些简单的问题
学习目标
重点
学习重点和难点
难点
应用全等图形的性质解决实际问题
寻找全等多边形的对应边、对应角;探究全等图形的性质
情境引入
找出右图中一对完全相同的的图形,并指出其与另一副图不同之处。
(1)
(2)
(3)
思考
全等图形的定义
这些图形中,有些是完全一样的,如果把它们叠在一起,它们就能重合
你能分别从图中找出这样的图形吗?
两个能够完全重合的图形称为全等图形
全等图形的判断
图中共有多少对全等图形,他们分别是
(1)
(2)
(3)
(4)
(5)
(10)
(7)
(8)
(9)
(14)
判定两个图形是否全等的基本方法是把他们重叠起来,看看他们是否能够互相重合,但在不少情况下, 无须把两个图形重叠在一起, 就知他们是否全等.
(6)
(11)
(12)
(13)
(15)
全等图形的特征
形状
相同
大小
相同
(1) 你能说出生活中全等图形的例子吗?
(2) 观察下面两组图形,它们是不是全等图形?
( 1 )
( 2 )
(3) 如果两个图形全等,它们的形状大小一定都相同吗?
全等图形的形状和大小都相同
观察图中的全等三角形应怎样表示?
注:记全等三角形时,通常把表示对应
顶点的字母写在对应的位置上.
△ ABC ≌△ DEF
全等三角形的性质
全等三角形的对应边相等,对应角相等.
(全等三角形的对应边相等)
(全等三角形的对应角相等)
∵△ABC≌ △A‘B’C‘
∴ AB=A’B‘, BC=B’C‘, AC=A’C‘
∴ ∠ A= ∠ A’, ∠ B= ∠B‘ ,
∠ C= ∠C’
图1中的全等的图形有( )
A 2组 B 3组
C 4组 D 5组
练习
B
练习
如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,
则BC=_____cm,∠B=_____.
B
A
E
F
C
3
64°
你还能求出哪些边的长度,
哪些角的度数?
下列各组图形是全等图形的是( )
B
练习
练习
如图,已知△ABC≌△DCB,且AB=DC,指出对应角和另外两组对边。
A
D
O
B
C
解:对应角为∠A和∠D,∠ABC和∠DCB,∠ACB和∠DBC,对应边还有AC和DB,BC和CB。
课堂小结
1、全等图形的概念
全等图形:能够 的两个图形称为全等图形
2、全等图形的特征
特征:全等图形的 和 都相同。
说明:(1)若事先知道两个全等图形,可得到它们的大小相同,即知道其中一个图形的面积可以求出另一个图形的面积。(2)全等图形的特征可作为判断两个图形全等的依据,先看它们的形状是否相同,再看大小是否相等。
大小
完全重合
形状
3、全等三角形
定义:能够完全重合的两个 叫做全等三角形。
对应顶点:能够重合的顶点。
对应边:能够重合的边。
对应角:能够重合的角。
4、全等三角形的性质
性质:全等三角形的对应边相等,对应角相等。
记法:用“≌” 表示,读作 “全等于”
注意:要把表示对应点的字母写在对应的位置上。
课堂小结
三角形
图片欣赏
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
