5.2 探索轴对称的性质 一课一练(含解析)
文档属性
| 名称 | 5.2 探索轴对称的性质 一课一练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 17:51:31 | ||
图片预览



文档简介
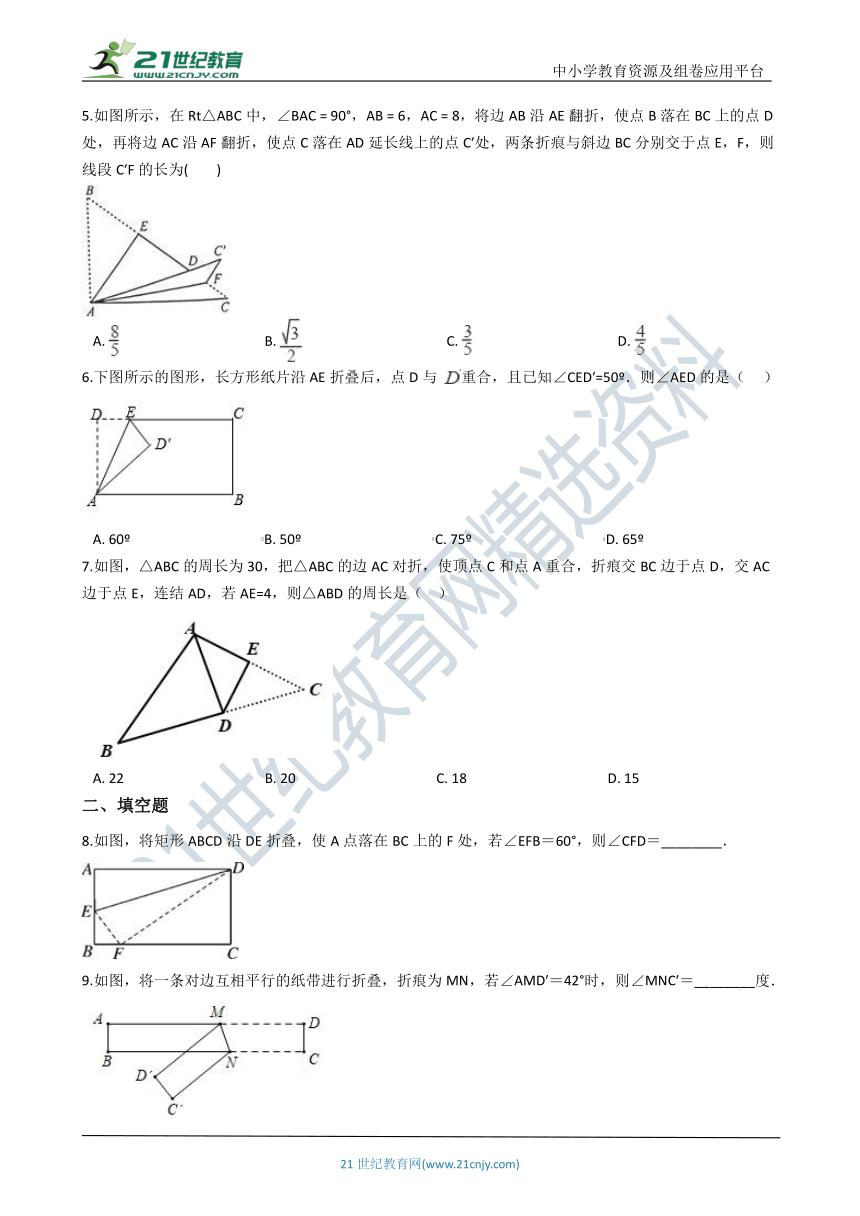
初中数学北师大版七年级下学期 第五章 5.2 探索轴对称的性质
一、单选题
1.下面各图形中,对称轴最多的是(?? )
A.?长方形???????????????????????????B.?正方形???????????????????????????C.?等边三角形???????????????????????????D.?等腰三角形
2.如图,点M,N在直线l的同侧,小东同学想通过作图在直线l上确定一点Q,使MQ与QN的和最小,那么下面的操作正确的是(?? )
A.????????????????????????????B.?
C.????????????????????????????D.?
3.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)(??? )
A.???????????B.???????????C.???????????D.?
4.如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED'=50°,则∠EFC等于(?? )
A.?65°?????????????????????????????????????B.?110°?????????????????????????????????????C.?115°?????????????????????????????????????D.?130°
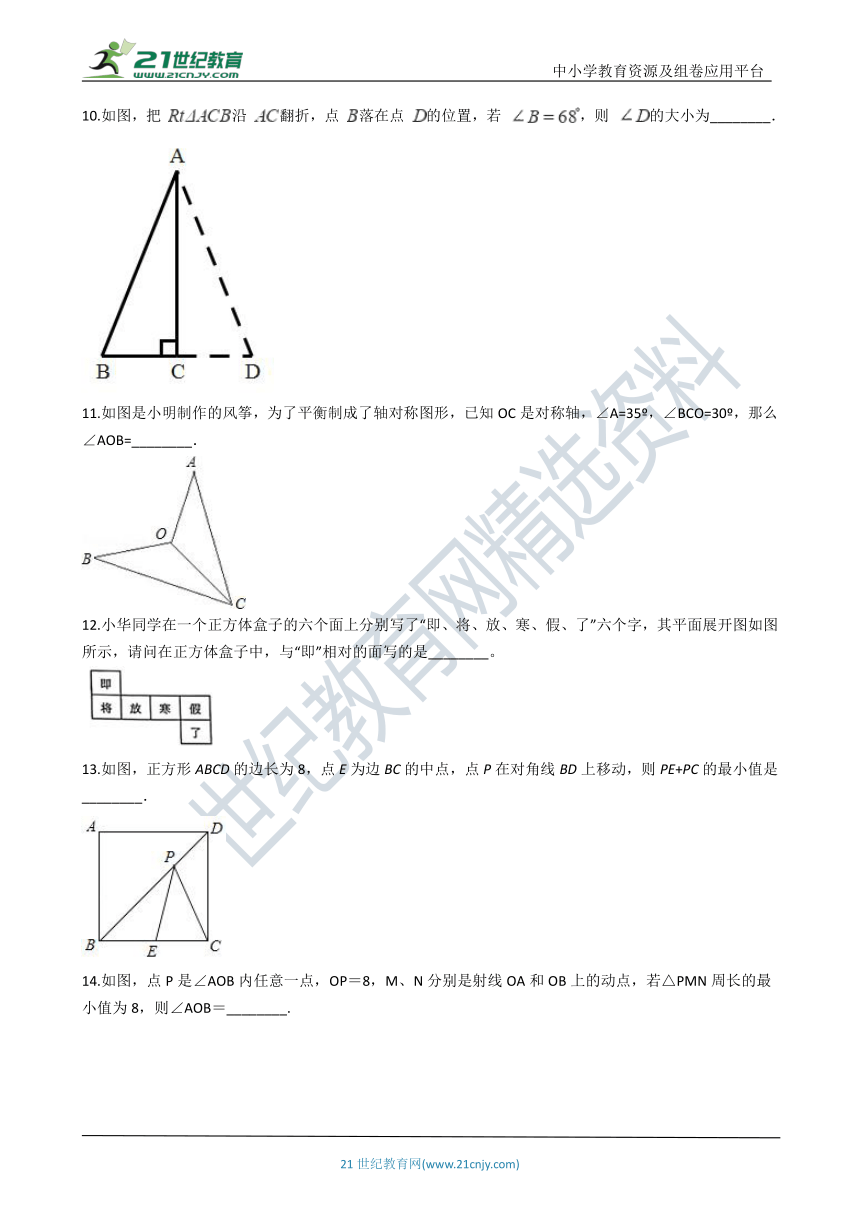
5.如图所示,在Rt△ABC中,∠BAC = 90°,AB = 6,AC = 8,将边AB沿AE翻折,使点B落在BC上的点D处,再将边AC沿AF翻折,使点C落在AD延长线上的点C′处,两条折痕与斜边BC分别交于点E,F,则线段C′F的长为(?????? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
6.下图所示的图形,长方形纸片沿AE折叠后,点D与 重合,且已知∠CED′=50?.则∠AED的是(??? )
A.?60???????????????????????????????????????B.?50???????????????????????????????????????C.?75???????????????????????????????????????D.?65?
7.如图,△ABC的周长为30,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连结AD,若AE=4,则△ABD的周长是( ??)
A.?22?????????????????????????????????????????B.?20?????????????????????????????????????????C.?18?????????????????????????????????????????D.?15
二、填空题
8.如图,将矩形ABCD沿DE折叠,使A点落在BC上的F处,若∠EFB=60°,则∠CFD=________.
9.如图,将一条对边互相平行的纸带进行折叠,折痕为MN,若∠AMD′=42°时,则∠MNC′=________度.
10.如图,把 沿 翻折,点 落在点 的位置,若 ,则 的大小为________.
11.如图是小明制作的风筝,为了平衡制成了轴对称图形,已知OC是对称轴,∠A=35?,∠BCO=30?,那么∠AOB=________.
12.小华同学在一个正方体盒子的六个面上分别写了“即、将、放、寒、假、了”六个字,其平面展开图如图所示,请问在正方体盒子中,与“即”相对的面写的是________。
13.如图,正方形ABCD的边长为8,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是________.
14.如图,点P是∠AOB内任意一点,OP=8,M、N分别是射线OA和OB上的动点,若△PMN周长的最小值为8,则∠AOB=________.
三、解答题
15.如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长.
16.如图,三角形纸片中,AB=8cm,BC=6cm,AC=5cm.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,求 的周长
17.如图,∠A=90°,点E为BC上一点,点A与点E关于BD对称,点B与点C关于DE对称,求∠C的度数.
答案解析部分
一、单选题
1.【答案】 B
解:∵长方形有两条对称轴,正方形有4条对称轴,
等边三角形有3条对称轴,等腰三角形有1条对称轴,
∴对称轴最多的是:正方形.
故答案为:B.
2.【答案】 C
解:作点M关于直线l的对称点M′,再连接M′N交l于点Q,则MQ+NQ=M′Q+NQ=M′N,由“两点之间,线段最短”,可知点Q即为所求.
故答案为:C
3.【答案】 D
解:根据河的两岸是平行直线,桥要与河岸垂直可知,只要AM+BN最短就符合题意,
即过A作河岸a的垂线AH,垂足为H,在直线AH上取点I,使AI等于河宽.连结IB交河岸b于N,作MN垂直于河岸交河岸a于M点,连接AM.
故答案为:D.
4.【答案】 C
解:∵∠AED′=50°,
∴∠DED′=180°﹣∠AED′=180°﹣50°=130°,
∵长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,
∴∠DEF=∠D′EF,
∴∠DEF= ∠DED′= ×130°=65°.
∵DE∥CF,
∴∠EFC=180°﹣∠DEF=115°.
故答案为:C.
5.【答案】 A
解:∵ 在Rt△ABC中,∠BAC=90°,AB=6,AC=8,
∴BC=10.
∵将边AB沿AE翻折,使点B落在BC上的点D处,
∴∠AEC=∠AEB,∠BAE=∠DAE.
∵∠BED=180°,
∴∠CEA=90°.
∵S△ABC=AB×AC=AE×BC,
∴AE=4.8,
∴.
∵将边AC沿AF翻折,使点C落在AD延长线上的点C′处,
∴CF=C′F,∠CAF=∠C′AF.
∵∠BAE+∠DAE+∠CAF+∠C′AF=∠BAC=90°,
∴∠EAF=45°,
∴∠EAF=∠EFA=45°,
∴AE=EF=4.8.
∵CF=CE-EF=6.4-4.8=1.6,
∴C′F=1.6=.
故答案为:A.
6.【答案】 D
解:由题意可得:∠AED′=∠AED.
?∵∠CED′+∠AED′+∠AED=180°,
?∴50°+2∠AED=180°,
?∴∠AED=65°.
?故答案为:D.
7.【答案】 A
解:依题可得,
AE=CE=4,CD=AD,
∴AC=8,
∵C△ABC=AB+BC+CA=30,
∴AB+BC=30-8=22,
∴C△ABD=AB+BD+DA=AB+BD+CD=AB+BC=22.
故答案为:A.
二、填空题
8.【答案】
解:∵矩形ABCD沿DE折叠,使A点落在BC上的F处
∴
∵∠EFB=60°
∴
故答案为: .
9.【答案】 111
解:由翻折可知:∠DMN=∠NMD′= (180°﹣42°)=69°,
∵AD∥BC,
∴∠DMN+∠MNC=180°,
∴∠MNC=111°,
由翻折可知:∠MNC′=∠MNC=111°,
故答案为:111.
10.【答案】
解:根据翻折变换的特点可知:
故答案为: .
11.【答案】 130°
解:依题意有∠AOB=2(∠A+∠ACO)=2(∠A+∠BCO)=130°.
即填:130°
12.【答案】 了
解:与“即”相对的面为“了”
13.【答案】
解:如图,连接AE ,
∵点C关于BD的对称点为点A,
∴PE+PC=PE+AP,
根据两点之间线段最短可得AE就是AP+PE的最小值,
∵正方形ABCD的边长为8,E是BC边的中点,
∴BE=4,
∴AE ,
故答案为: .
14.【答案】 30°
解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
∴OC=OP=OD,∠AOB= ∠COD,
∵△PMN周长的最小值是8,
∴PM+PN+MN=8,
∴DM+CN+MN=8,即CD=8=OP,
∴OC=OD=CD,即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°,
故答案为:30°.
三、解答题
15.【答案】 解:因为DE是△ABE的对称轴,
所以AE=BE.
所以C△BCE=BC+CE+BE=BC+CE+AE=BC+AC=14.
因为BC=6,所以AC=8.
所以AB=AC=8.
16.【答案】 解:∵BC沿BD折叠点C落在AB边上的点E处,
∴DE=CD,BE=BC,
∵AB=8cm,BC=6cm,
∴AE=AB-BE=AB-BC=8-6=2cm,
∴△ADE的周长=AD+DE+AE,
=AD+CD+AE,
=AC+AE,
=5+2,
=7cm.
17.【答案】 解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD,
又B点、C点关于DE对称,
∴∠DBE=∠C,
∴∠ABC=2∠C,
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°,
∴∠C=30°.
一、单选题
1.下面各图形中,对称轴最多的是(?? )
A.?长方形???????????????????????????B.?正方形???????????????????????????C.?等边三角形???????????????????????????D.?等腰三角形
2.如图,点M,N在直线l的同侧,小东同学想通过作图在直线l上确定一点Q,使MQ与QN的和最小,那么下面的操作正确的是(?? )
A.????????????????????????????B.?
C.????????????????????????????D.?
3.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)(??? )
A.???????????B.???????????C.???????????D.?
4.如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED'=50°,则∠EFC等于(?? )
A.?65°?????????????????????????????????????B.?110°?????????????????????????????????????C.?115°?????????????????????????????????????D.?130°
5.如图所示,在Rt△ABC中,∠BAC = 90°,AB = 6,AC = 8,将边AB沿AE翻折,使点B落在BC上的点D处,再将边AC沿AF翻折,使点C落在AD延长线上的点C′处,两条折痕与斜边BC分别交于点E,F,则线段C′F的长为(?????? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
6.下图所示的图形,长方形纸片沿AE折叠后,点D与 重合,且已知∠CED′=50?.则∠AED的是(??? )
A.?60???????????????????????????????????????B.?50???????????????????????????????????????C.?75???????????????????????????????????????D.?65?
7.如图,△ABC的周长为30,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连结AD,若AE=4,则△ABD的周长是( ??)
A.?22?????????????????????????????????????????B.?20?????????????????????????????????????????C.?18?????????????????????????????????????????D.?15
二、填空题
8.如图,将矩形ABCD沿DE折叠,使A点落在BC上的F处,若∠EFB=60°,则∠CFD=________.
9.如图,将一条对边互相平行的纸带进行折叠,折痕为MN,若∠AMD′=42°时,则∠MNC′=________度.
10.如图,把 沿 翻折,点 落在点 的位置,若 ,则 的大小为________.
11.如图是小明制作的风筝,为了平衡制成了轴对称图形,已知OC是对称轴,∠A=35?,∠BCO=30?,那么∠AOB=________.
12.小华同学在一个正方体盒子的六个面上分别写了“即、将、放、寒、假、了”六个字,其平面展开图如图所示,请问在正方体盒子中,与“即”相对的面写的是________。
13.如图,正方形ABCD的边长为8,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是________.
14.如图,点P是∠AOB内任意一点,OP=8,M、N分别是射线OA和OB上的动点,若△PMN周长的最小值为8,则∠AOB=________.
三、解答题
15.如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长.
16.如图,三角形纸片中,AB=8cm,BC=6cm,AC=5cm.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,求 的周长
17.如图,∠A=90°,点E为BC上一点,点A与点E关于BD对称,点B与点C关于DE对称,求∠C的度数.
答案解析部分
一、单选题
1.【答案】 B
解:∵长方形有两条对称轴,正方形有4条对称轴,
等边三角形有3条对称轴,等腰三角形有1条对称轴,
∴对称轴最多的是:正方形.
故答案为:B.
2.【答案】 C
解:作点M关于直线l的对称点M′,再连接M′N交l于点Q,则MQ+NQ=M′Q+NQ=M′N,由“两点之间,线段最短”,可知点Q即为所求.
故答案为:C
3.【答案】 D
解:根据河的两岸是平行直线,桥要与河岸垂直可知,只要AM+BN最短就符合题意,
即过A作河岸a的垂线AH,垂足为H,在直线AH上取点I,使AI等于河宽.连结IB交河岸b于N,作MN垂直于河岸交河岸a于M点,连接AM.
故答案为:D.
4.【答案】 C
解:∵∠AED′=50°,
∴∠DED′=180°﹣∠AED′=180°﹣50°=130°,
∵长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,
∴∠DEF=∠D′EF,
∴∠DEF= ∠DED′= ×130°=65°.
∵DE∥CF,
∴∠EFC=180°﹣∠DEF=115°.
故答案为:C.
5.【答案】 A
解:∵ 在Rt△ABC中,∠BAC=90°,AB=6,AC=8,
∴BC=10.
∵将边AB沿AE翻折,使点B落在BC上的点D处,
∴∠AEC=∠AEB,∠BAE=∠DAE.
∵∠BED=180°,
∴∠CEA=90°.
∵S△ABC=AB×AC=AE×BC,
∴AE=4.8,
∴.
∵将边AC沿AF翻折,使点C落在AD延长线上的点C′处,
∴CF=C′F,∠CAF=∠C′AF.
∵∠BAE+∠DAE+∠CAF+∠C′AF=∠BAC=90°,
∴∠EAF=45°,
∴∠EAF=∠EFA=45°,
∴AE=EF=4.8.
∵CF=CE-EF=6.4-4.8=1.6,
∴C′F=1.6=.
故答案为:A.
6.【答案】 D
解:由题意可得:∠AED′=∠AED.
?∵∠CED′+∠AED′+∠AED=180°,
?∴50°+2∠AED=180°,
?∴∠AED=65°.
?故答案为:D.
7.【答案】 A
解:依题可得,
AE=CE=4,CD=AD,
∴AC=8,
∵C△ABC=AB+BC+CA=30,
∴AB+BC=30-8=22,
∴C△ABD=AB+BD+DA=AB+BD+CD=AB+BC=22.
故答案为:A.
二、填空题
8.【答案】
解:∵矩形ABCD沿DE折叠,使A点落在BC上的F处
∴
∵∠EFB=60°
∴
故答案为: .
9.【答案】 111
解:由翻折可知:∠DMN=∠NMD′= (180°﹣42°)=69°,
∵AD∥BC,
∴∠DMN+∠MNC=180°,
∴∠MNC=111°,
由翻折可知:∠MNC′=∠MNC=111°,
故答案为:111.
10.【答案】
解:根据翻折变换的特点可知:
故答案为: .
11.【答案】 130°
解:依题意有∠AOB=2(∠A+∠ACO)=2(∠A+∠BCO)=130°.
即填:130°
12.【答案】 了
解:与“即”相对的面为“了”
13.【答案】
解:如图,连接AE ,
∵点C关于BD的对称点为点A,
∴PE+PC=PE+AP,
根据两点之间线段最短可得AE就是AP+PE的最小值,
∵正方形ABCD的边长为8,E是BC边的中点,
∴BE=4,
∴AE ,
故答案为: .
14.【答案】 30°
解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
∴OC=OP=OD,∠AOB= ∠COD,
∵△PMN周长的最小值是8,
∴PM+PN+MN=8,
∴DM+CN+MN=8,即CD=8=OP,
∴OC=OD=CD,即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°,
故答案为:30°.
三、解答题
15.【答案】 解:因为DE是△ABE的对称轴,
所以AE=BE.
所以C△BCE=BC+CE+BE=BC+CE+AE=BC+AC=14.
因为BC=6,所以AC=8.
所以AB=AC=8.
16.【答案】 解:∵BC沿BD折叠点C落在AB边上的点E处,
∴DE=CD,BE=BC,
∵AB=8cm,BC=6cm,
∴AE=AB-BE=AB-BC=8-6=2cm,
∴△ADE的周长=AD+DE+AE,
=AD+CD+AE,
=AC+AE,
=5+2,
=7cm.
17.【答案】 解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD,
又B点、C点关于DE对称,
∴∠DBE=∠C,
∴∠ABC=2∠C,
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°,
∴∠C=30°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
