5.3 简单的轴对称图形 一课一练(含解析)
文档属性
| 名称 | 5.3 简单的轴对称图形 一课一练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 17:52:47 | ||
图片预览


文档简介
初中数学北师大版七年级下学期 第五章 5.3 简单的轴对称图形
一、单选题
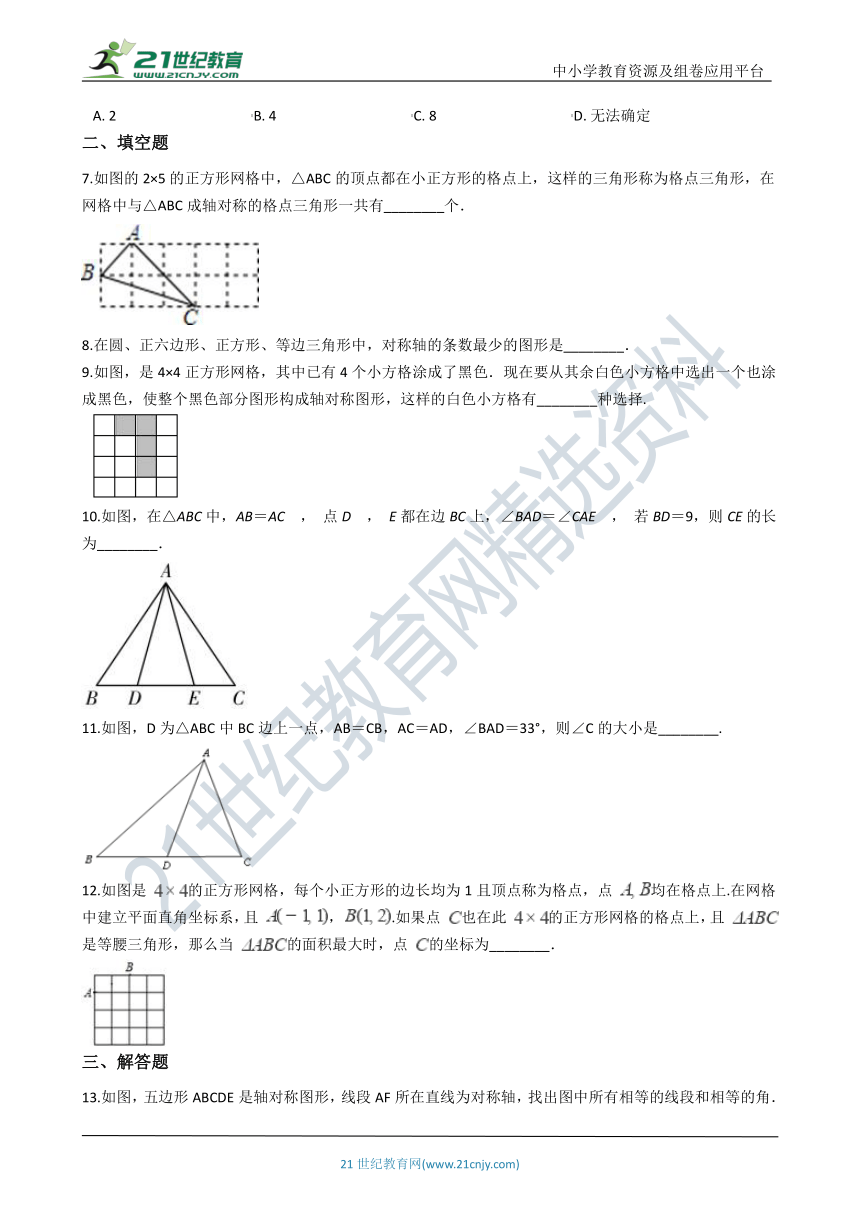
1.下列图形是对圆的面积进行四等分的几种作图,则它们是轴对称图形的个数为(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
2.如图,在4×4的正方形网格中,已将图中的三个小正方形涂上阴影,若再将图中其余小正方形任选一个也涂上阴影,使得整个阴影部分是轴对称图形,那么符合条件的小正方形共有(? )
A.???????????????????????????????????????B.?5个??????????????????????????????????????C.?4个??????????????????????????????????????D.?3个
3.如图,与线段a、b可以构成轴对称图形的是(??? )
A.?线段 ????????????????????????????????B.?线段 ????????????????????????????????C.?线段 ????????????????????????????????D.?线段
4.一个正五边形的对称轴共有(?? )
A.?1条??????????????????????????????????????B.?3条??????????????????????????????????????C.?5条??????????????????????????????????????D.?10条
5.下列图形中,其对称轴条数最多的是(?? )
A.?正方形????????????????????????????????B.?矩形????????????????????????????????C.?菱形????????????????????????????????D.?等边三角形
6.如图,正方形的边长为2,则图中阴影部分的面积为(??? )
A.?2???????????????????????????????????????B.?4???????????????????????????????????????C.?8???????????????????????????????????????D.?无法确定
二、填空题
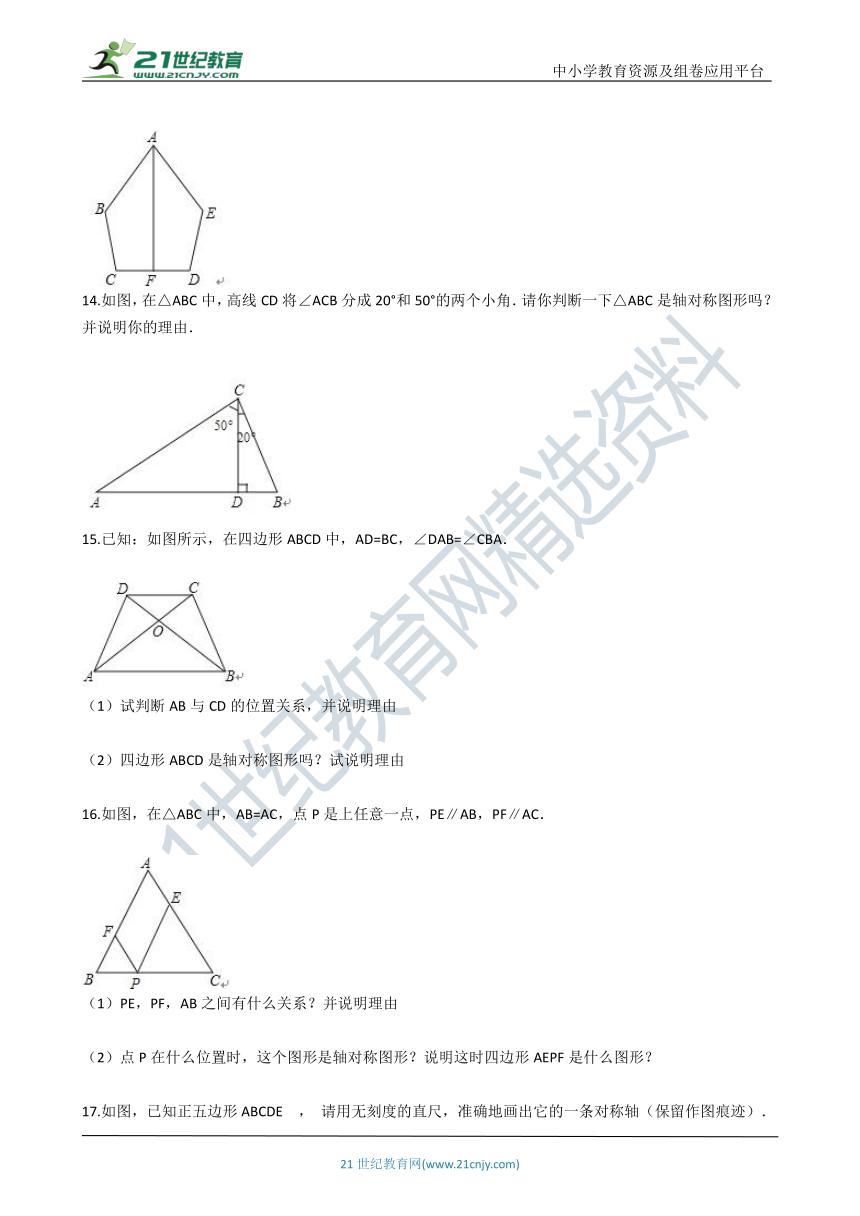
7.如图的2×5的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有________个.
8.在圆、正六边形、正方形、等边三角形中,对称轴的条数最少的图形是________.
9.如图,是4×4正方形网格,其中已有4个小方格涂成了黑色.现在要从其余白色小方格中选出一个也涂成黑色,使整个黑色部分图形构成轴对称图形,这样的白色小方格有________种选择.
10.如图,在△ABC中,AB=AC , 点D , E都在边BC上,∠BAD=∠CAE , 若BD=9,则CE的长为________.
11.如图,D为△ABC中BC边上一点,AB=CB,AC=AD,∠BAD=33°,则∠C的大小是________.
12.如图是 的正方形网格,每个小正方形的边长均为1且顶点称为格点,点 均在格点上.在网格中建立平面直角坐标系,且 , .如果点 也在此 的正方形网格的格点上,且 是等腰三角形,那么当 的面积最大时,点 的坐标为________.
三、解答题
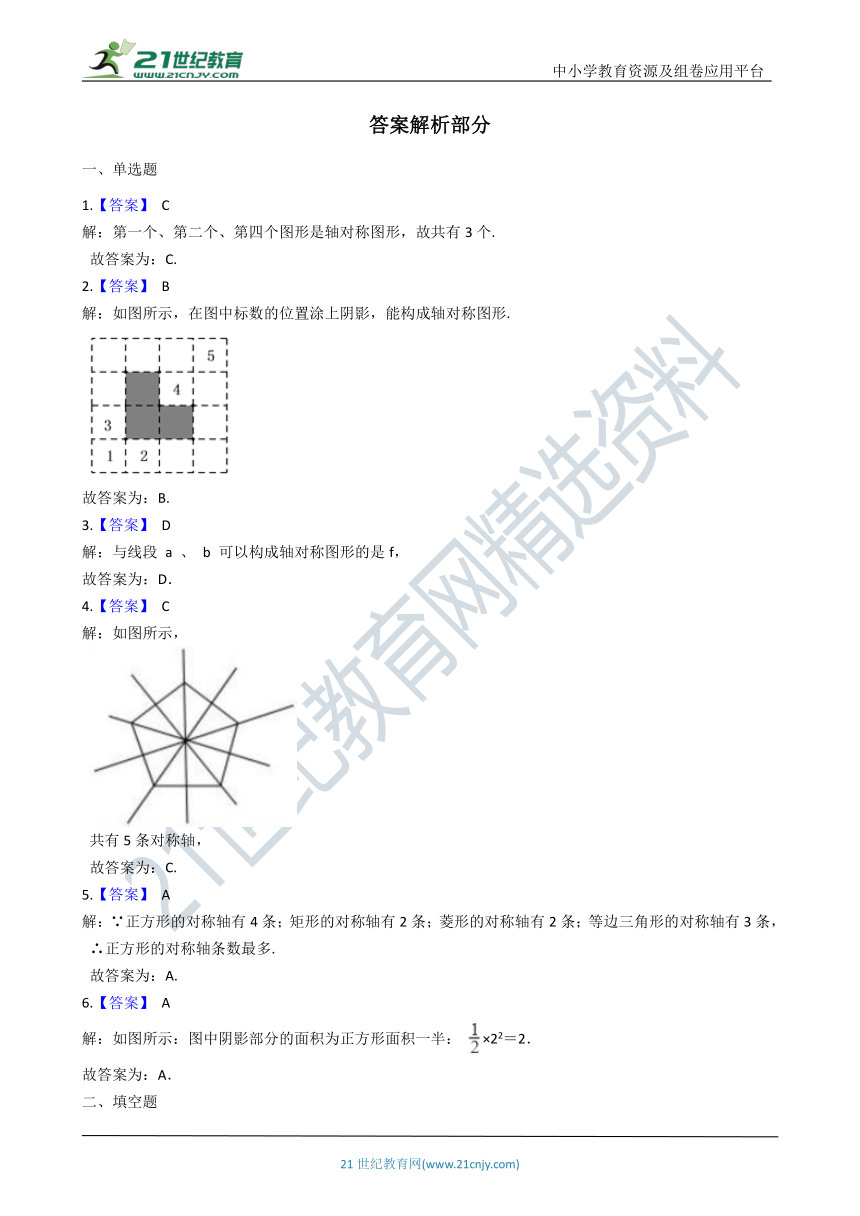
13.如图,五边形ABCDE是轴对称图形,线段AF所在直线为对称轴,找出图中所有相等的线段和相等的角.
?
14.如图,在△ABC中,高线CD将∠ACB分成20°和50°的两个小角.请你判断一下△ABC是轴对称图形吗?并说明你的理由.
?
15.已知:如图所示,在四边形ABCD中,AD=BC,∠DAB=∠CBA.
(1)试判断AB与CD的位置关系,并说明理由
(2)四边形ABCD是轴对称图形吗?试说明理由
16.如图,在△ABC中,AB=AC,点P是上任意一点,PE∥AB,PF∥AC.
?
(1)PE,PF,AB之间有什么关系?并说明理由
(2)点P在什么位置时,这个图形是轴对称图形?说明这时四边形AEPF是什么图形?
17.如图,已知正五边形ABCDE , 请用无刻度的直尺,准确地画出它的一条对称轴(保留作图痕迹).
18.为了加强环境治理,某地准备在如图所示的公路m、n之间的S区域新建一座垃圾处理站P,按照设计要求,垃圾处理站P到区域S内的两个城镇A、B的距离必须相等,到两条公路m、n的距离也必须相等.请在图中用尺规作图的方法作出点P的位置并标出点P(不写作法但保留作图痕迹).
19.图1,图2都是由边长为1的小等边三角形构成的网格,△ABC为格点三角形.请仅用无刻度直尺在网格中完成下列画图.
(1)在图1中,画出△ABC中AB边上的中线CM;
(2)在图2中,画出∠APC,使∠APC=∠ABC,且点P是格点(画出一个即可).
20.如图,已知等腰三角形 的顶角 .
(1)在 上作一点 ,使 (要求:尺规作图,保留作图痕迹,不必写作法和证明).
(2)写出 的度数.
答案解析部分
一、单选题
1.【答案】 C
解:第一个、第二个、第四个图形是轴对称图形,故共有3个.
故答案为:C.
2.【答案】 B
解:如图所示,在图中标数的位置涂上阴影,能构成轴对称图形.
故答案为:B.
3.【答案】 D
解:与线段 a 、 b 可以构成轴对称图形的是f,
故答案为:D.
4.【答案】 C
解:如图所示,
共有5条对称轴,
故答案为:C.
5.【答案】 A
解:∵正方形的对称轴有4条;矩形的对称轴有2条;菱形的对称轴有2条;等边三角形的对称轴有3条,
∴正方形的对称轴条数最多.
故答案为:A.
6.【答案】 A
解:如图所示:图中阴影部分的面积为正方形面积一半: ×22=2.
故答案为:A.
二、填空题
7.【答案】 4
解:如图所示,对称轴有三种位置,与△ABC成轴对称的格点三角形有4个.
故答案为:4.
8.【答案】 等边三角形
解:圆有无数条对称轴,等边三角形有3条对称轴,正方形有4条对称轴,正六边形有6条对称轴;故对称轴的条数最少的图形是等边三角形.
9.【答案】 3
解:如下图,这样的白色小方格共有3种选择.
10.【答案】 9
解:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中
∴△ABD≌△ACE(ASA)
∴CE=BD=9.
故答案为:9.
11.【答案】 71°
解:∵AB=CB,AC=AD,
∴ , ,
∵∠BAD=33°,
∴ ,
∵ ,
∴ ,
∴ ;
故答案为71°.
12.【答案】 (0,-1);(2,0)
解:建立平面直角坐标系如图所示,故以AB为腰作等腰直角三角形面积最大,
∴当 的面积最大时,点 的坐标为(0,-1);(2,0).
故填:(0,-1);(2,0)
三、解答题
13.【答案】 解:相等的线段:AB=AE,CB=DE,CF=DF;
相等的角:∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFD=∠AFC.
14.【答案】 解:△ABC是轴对称图形.
∵∠BCD=20°,
∴∠B=90°﹣∠BCD=70°,
∴∠ACB=∠B=70°,
∴△ABC是等腰三角形,
∴△ABC是轴对称图形.
15.【答案】 (1)解:
AB∥CD.理由如下:
在△ABD和△BAC中
.
∴△ABD≌△BAC(SAS).
∴∠OAB=∠OBA,BD=AC.
∴OA=OB.
∴AC﹣OA=BD﹣OB.
∴OD=OC.
∴∠ODC=∠OCD.
∵∠ODC+∠OCD+∠COD=180°,
∠OAB+∠OBA+∠AOB=180°,
∴2∠ODC+∠COD=180°.
2∠OBA+∠AOB=180°.
又∠COD=∠AOB,
∴∠CDO=∠OBA.
∴AB∥CD.
(2)解:
四边形ABCD是轴对称图形.理由如下:
延长AD、BC交于点P,
∵∠DAB=∠CBA,
∴AP=BP.
∴点P在AB的垂直平分线上.
又OA=OB,∴点O在AB的垂直平分线上.
∴OP垂直平分线段AB,
∴点A与点B关于直线OP对称①.
∵AB∥DC,
∴∠PDC=∠PAB∠PCD=∠PBA.
∴∠PDC=∠PCD.
∴DP=CP,∴点P在DC的垂直平分线上.
又OD=OC,∴点O在DC的垂直平分线上.
∴OP垂直平分线段DC.
∴点C与点D关于直线OP对称②.
所以,综上①②所述,四边形ABCD是轴对称图形.
16.【答案】 (1)解:
∵AB=AC,
∴∠B=∠C,
∵PE∥AB,PF∥AC.
∴∠BPF=∠C,四边形AEPF是平行四边形.
∴∠B=∠BPF,AF=PE,
∴BF=PF,
∴PE+PF=AF+BF=AB.
(2)解:P为中点时是轴对称图形,四边形AEPF是为菱形.
17.【答案】
解:如图所示,直线AK即为所求的一条对称轴(解答不唯一).
18.【答案】 解:如图所示,点P即为所求作.
19.【答案】 解:(1)如图所示,线段CM即为所求;
(2)如图所示,点P即为所求.
20.【答案】 (1)解:如图,点 即为所求;
(2)解:连接 ,∵ , ,
∴ ,
由(1)得: ,
∴ ,
.
一、单选题
1.下列图形是对圆的面积进行四等分的几种作图,则它们是轴对称图形的个数为(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
2.如图,在4×4的正方形网格中,已将图中的三个小正方形涂上阴影,若再将图中其余小正方形任选一个也涂上阴影,使得整个阴影部分是轴对称图形,那么符合条件的小正方形共有(? )
A.???????????????????????????????????????B.?5个??????????????????????????????????????C.?4个??????????????????????????????????????D.?3个
3.如图,与线段a、b可以构成轴对称图形的是(??? )
A.?线段 ????????????????????????????????B.?线段 ????????????????????????????????C.?线段 ????????????????????????????????D.?线段
4.一个正五边形的对称轴共有(?? )
A.?1条??????????????????????????????????????B.?3条??????????????????????????????????????C.?5条??????????????????????????????????????D.?10条
5.下列图形中,其对称轴条数最多的是(?? )
A.?正方形????????????????????????????????B.?矩形????????????????????????????????C.?菱形????????????????????????????????D.?等边三角形
6.如图,正方形的边长为2,则图中阴影部分的面积为(??? )
A.?2???????????????????????????????????????B.?4???????????????????????????????????????C.?8???????????????????????????????????????D.?无法确定
二、填空题
7.如图的2×5的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有________个.
8.在圆、正六边形、正方形、等边三角形中,对称轴的条数最少的图形是________.
9.如图,是4×4正方形网格,其中已有4个小方格涂成了黑色.现在要从其余白色小方格中选出一个也涂成黑色,使整个黑色部分图形构成轴对称图形,这样的白色小方格有________种选择.
10.如图,在△ABC中,AB=AC , 点D , E都在边BC上,∠BAD=∠CAE , 若BD=9,则CE的长为________.
11.如图,D为△ABC中BC边上一点,AB=CB,AC=AD,∠BAD=33°,则∠C的大小是________.
12.如图是 的正方形网格,每个小正方形的边长均为1且顶点称为格点,点 均在格点上.在网格中建立平面直角坐标系,且 , .如果点 也在此 的正方形网格的格点上,且 是等腰三角形,那么当 的面积最大时,点 的坐标为________.
三、解答题
13.如图,五边形ABCDE是轴对称图形,线段AF所在直线为对称轴,找出图中所有相等的线段和相等的角.
?
14.如图,在△ABC中,高线CD将∠ACB分成20°和50°的两个小角.请你判断一下△ABC是轴对称图形吗?并说明你的理由.
?
15.已知:如图所示,在四边形ABCD中,AD=BC,∠DAB=∠CBA.
(1)试判断AB与CD的位置关系,并说明理由
(2)四边形ABCD是轴对称图形吗?试说明理由
16.如图,在△ABC中,AB=AC,点P是上任意一点,PE∥AB,PF∥AC.
?
(1)PE,PF,AB之间有什么关系?并说明理由
(2)点P在什么位置时,这个图形是轴对称图形?说明这时四边形AEPF是什么图形?
17.如图,已知正五边形ABCDE , 请用无刻度的直尺,准确地画出它的一条对称轴(保留作图痕迹).
18.为了加强环境治理,某地准备在如图所示的公路m、n之间的S区域新建一座垃圾处理站P,按照设计要求,垃圾处理站P到区域S内的两个城镇A、B的距离必须相等,到两条公路m、n的距离也必须相等.请在图中用尺规作图的方法作出点P的位置并标出点P(不写作法但保留作图痕迹).
19.图1,图2都是由边长为1的小等边三角形构成的网格,△ABC为格点三角形.请仅用无刻度直尺在网格中完成下列画图.
(1)在图1中,画出△ABC中AB边上的中线CM;
(2)在图2中,画出∠APC,使∠APC=∠ABC,且点P是格点(画出一个即可).
20.如图,已知等腰三角形 的顶角 .
(1)在 上作一点 ,使 (要求:尺规作图,保留作图痕迹,不必写作法和证明).
(2)写出 的度数.
答案解析部分
一、单选题
1.【答案】 C
解:第一个、第二个、第四个图形是轴对称图形,故共有3个.
故答案为:C.
2.【答案】 B
解:如图所示,在图中标数的位置涂上阴影,能构成轴对称图形.
故答案为:B.
3.【答案】 D
解:与线段 a 、 b 可以构成轴对称图形的是f,
故答案为:D.
4.【答案】 C
解:如图所示,
共有5条对称轴,
故答案为:C.
5.【答案】 A
解:∵正方形的对称轴有4条;矩形的对称轴有2条;菱形的对称轴有2条;等边三角形的对称轴有3条,
∴正方形的对称轴条数最多.
故答案为:A.
6.【答案】 A
解:如图所示:图中阴影部分的面积为正方形面积一半: ×22=2.
故答案为:A.
二、填空题
7.【答案】 4
解:如图所示,对称轴有三种位置,与△ABC成轴对称的格点三角形有4个.
故答案为:4.
8.【答案】 等边三角形
解:圆有无数条对称轴,等边三角形有3条对称轴,正方形有4条对称轴,正六边形有6条对称轴;故对称轴的条数最少的图形是等边三角形.
9.【答案】 3
解:如下图,这样的白色小方格共有3种选择.
10.【答案】 9
解:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中
∴△ABD≌△ACE(ASA)
∴CE=BD=9.
故答案为:9.
11.【答案】 71°
解:∵AB=CB,AC=AD,
∴ , ,
∵∠BAD=33°,
∴ ,
∵ ,
∴ ,
∴ ;
故答案为71°.
12.【答案】 (0,-1);(2,0)
解:建立平面直角坐标系如图所示,故以AB为腰作等腰直角三角形面积最大,
∴当 的面积最大时,点 的坐标为(0,-1);(2,0).
故填:(0,-1);(2,0)
三、解答题
13.【答案】 解:相等的线段:AB=AE,CB=DE,CF=DF;
相等的角:∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFD=∠AFC.
14.【答案】 解:△ABC是轴对称图形.
∵∠BCD=20°,
∴∠B=90°﹣∠BCD=70°,
∴∠ACB=∠B=70°,
∴△ABC是等腰三角形,
∴△ABC是轴对称图形.
15.【答案】 (1)解:
AB∥CD.理由如下:
在△ABD和△BAC中
.
∴△ABD≌△BAC(SAS).
∴∠OAB=∠OBA,BD=AC.
∴OA=OB.
∴AC﹣OA=BD﹣OB.
∴OD=OC.
∴∠ODC=∠OCD.
∵∠ODC+∠OCD+∠COD=180°,
∠OAB+∠OBA+∠AOB=180°,
∴2∠ODC+∠COD=180°.
2∠OBA+∠AOB=180°.
又∠COD=∠AOB,
∴∠CDO=∠OBA.
∴AB∥CD.
(2)解:
四边形ABCD是轴对称图形.理由如下:
延长AD、BC交于点P,
∵∠DAB=∠CBA,
∴AP=BP.
∴点P在AB的垂直平分线上.
又OA=OB,∴点O在AB的垂直平分线上.
∴OP垂直平分线段AB,
∴点A与点B关于直线OP对称①.
∵AB∥DC,
∴∠PDC=∠PAB∠PCD=∠PBA.
∴∠PDC=∠PCD.
∴DP=CP,∴点P在DC的垂直平分线上.
又OD=OC,∴点O在DC的垂直平分线上.
∴OP垂直平分线段DC.
∴点C与点D关于直线OP对称②.
所以,综上①②所述,四边形ABCD是轴对称图形.
16.【答案】 (1)解:
∵AB=AC,
∴∠B=∠C,
∵PE∥AB,PF∥AC.
∴∠BPF=∠C,四边形AEPF是平行四边形.
∴∠B=∠BPF,AF=PE,
∴BF=PF,
∴PE+PF=AF+BF=AB.
(2)解:P为中点时是轴对称图形,四边形AEPF是为菱形.
17.【答案】
解:如图所示,直线AK即为所求的一条对称轴(解答不唯一).
18.【答案】 解:如图所示,点P即为所求作.
19.【答案】 解:(1)如图所示,线段CM即为所求;
(2)如图所示,点P即为所求.
20.【答案】 (1)解:如图,点 即为所求;
(2)解:连接 ,∵ , ,
∴ ,
由(1)得: ,
∴ ,
.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
