19.1.1 平行四边形的定义及性质1
文档属性
| 名称 | 19.1.1 平行四边形的定义及性质1 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-16 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
-------毕达哥拉斯
平行四边形的性质
取出两张全等的三角形纸片拼平行四边形,你能拼出几种不同的平行四边形
平行四边形相对的两边有怎样的位置关系?
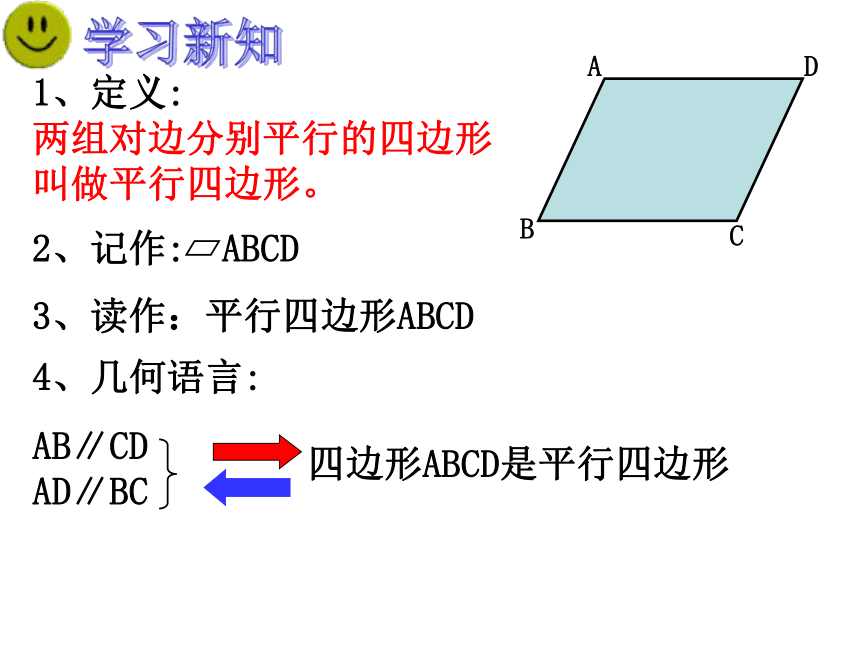
1、定义:
两组对边分别平行的四边形叫做平行四边形。
2、记作:
ABCD
3、读作:平行四边形ABCD
4、几何语言:
四边形ABCD是平行四边形
AB∥CD AD∥BC
A
B
C
D
A
B
C
D
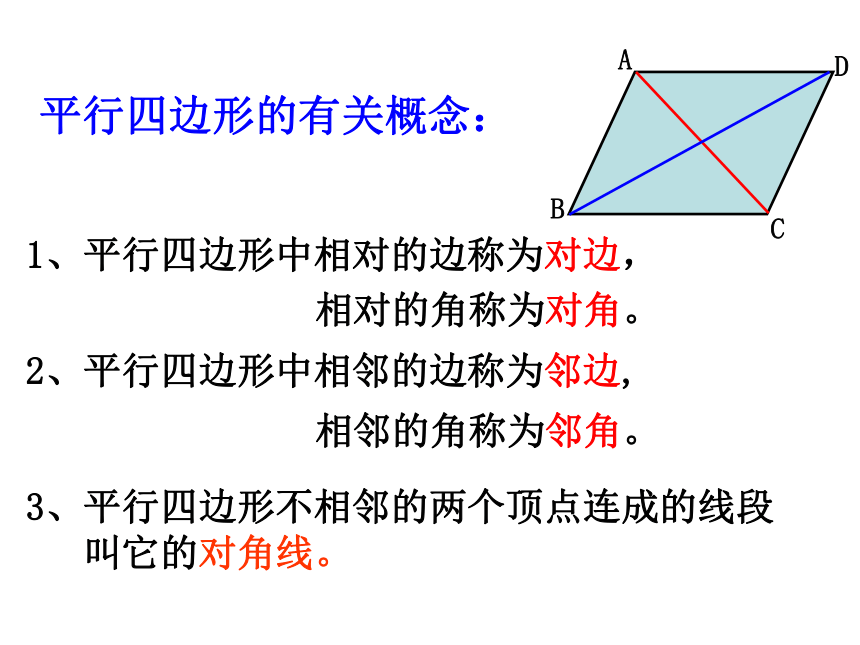
1、平行四边形中相对的边称为对边,
相对的角称为对角。
2、平行四边形中相邻的边称为邻边,
相邻的角称为邻角。
平行四边形的有关概念:
3、平行四边形不相邻的两个顶点连成的线段
叫它的对角线。
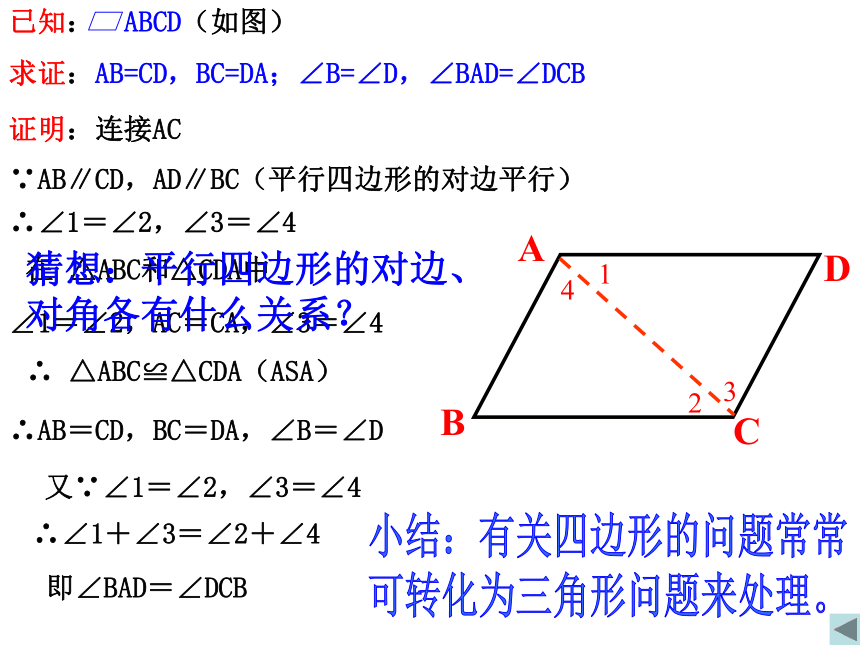
已知: ABCD(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连接AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
∠1=∠2,AC=CA,∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠3=∠2+∠4
在 △ABC和△CDA中
A
B
C
D
1
2
3
4
猜想:平行四边形的对边、 对角各有什么关系?
1、在本子上画一个平行四边形,并把它表示出来。
2、画出平行四边形的两条对角线。
3、你有什么发现?
平行四边形的性质:
平行四边形的对边平行且相等;
平行四边形的对角相等;邻角互补。
边:
角:
∵四边形ABCD是平行四边形
∴AB∥CD AD∥BC
∵四边形ABCD是平行四边形
∴∠A=∠C ∠B=∠D
∠A+∠C=180°∠B+∠D=180°…
1、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:
四边形ABCD是平行四边形
2、已知一个平行四边形的两个内角之比为1︰2,你能求出平行四边形每个内角的度数吗
A
B
C
D
3、已知如图,在 ABCD中,
求证:①△ABE≌△CDF
A
B
C
D
E
F
②AE=CF
E、F分别是边BC和AD上的点,且BE=DF。
A
B
C
D
A
B
C
D
如图,在 ABCD中,BE平分∠ABC交AD于E,BC=8㎝,CD=6㎝, ∠D=60°,则下列说法中错误的是( )
∠C=120° B. AE=6 ㎝
C. AD=8 ㎝ D. ∠BED=140 °
A
B
C
D
E
D
A
B
C
D
如图, ABCD的周长是24 ㎝,对角线AC把它分成两个周长为17 ㎝的三角形,则对角线AC的长为( )
A、4 ㎝ B、5 ㎝
C、7 ㎝ D、8 ㎝
B
A
B
C
D
A
B
C
D
如图,在 ABCD中,AB=6 ㎝,BC=8 ㎝,
∠B=30°,则 ABCD的面积为( )
A、48 ㎝2 B、14 ㎝2
C、24 ㎝2 D、12 ㎝2
A
B
C
D
C
A
B
C
D
如图, ABCD中,AE BC,AF CD, ∠B=60°
BE=2,DF=3。则 ABCD的周长为( )
A、20 B、12
C、20 D、12
A
B
C
D
E
F
C
如图,在 ABCD中,AC=4 ㎝ ,CD=3 ㎝ ,BC=5 ㎝ ,则
ABCD的面积为 ________ .
A
D
C
B
4
5
3
12㎝2
如图, ABCD中,AB=8㎝,BC=6㎝,∠A=30°,点P从点A 出发沿AB以每秒1厘米的速度向点B移动。
(1)当P点运动了几秒时,△PBC为等腰三角形;
(2)设△PBC的面积为y,请写出y关于点P的运动时间t的函数关系式,并写出t的取值范围;
(3)是否存在一点P,使S△PBC= S ABCD?
A
B
C
D
P
8-t
t
6
E
)
30°
)
30°
作 业
全效学习63-64
(当堂测评、分层作业)
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
-------毕达哥拉斯
平行四边形的性质
取出两张全等的三角形纸片拼平行四边形,你能拼出几种不同的平行四边形
平行四边形相对的两边有怎样的位置关系?
1、定义:
两组对边分别平行的四边形叫做平行四边形。
2、记作:
ABCD
3、读作:平行四边形ABCD
4、几何语言:
四边形ABCD是平行四边形
AB∥CD AD∥BC
A
B
C
D
A
B
C
D
1、平行四边形中相对的边称为对边,
相对的角称为对角。
2、平行四边形中相邻的边称为邻边,
相邻的角称为邻角。
平行四边形的有关概念:
3、平行四边形不相邻的两个顶点连成的线段
叫它的对角线。
已知: ABCD(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连接AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
∠1=∠2,AC=CA,∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠3=∠2+∠4
在 △ABC和△CDA中
A
B
C
D
1
2
3
4
猜想:平行四边形的对边、 对角各有什么关系?
1、在本子上画一个平行四边形,并把它表示出来。
2、画出平行四边形的两条对角线。
3、你有什么发现?
平行四边形的性质:
平行四边形的对边平行且相等;
平行四边形的对角相等;邻角互补。
边:
角:
∵四边形ABCD是平行四边形
∴AB∥CD AD∥BC
∵四边形ABCD是平行四边形
∴∠A=∠C ∠B=∠D
∠A+∠C=180°∠B+∠D=180°…
1、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:
四边形ABCD是平行四边形
2、已知一个平行四边形的两个内角之比为1︰2,你能求出平行四边形每个内角的度数吗
A
B
C
D
3、已知如图,在 ABCD中,
求证:①△ABE≌△CDF
A
B
C
D
E
F
②AE=CF
E、F分别是边BC和AD上的点,且BE=DF。
A
B
C
D
A
B
C
D
如图,在 ABCD中,BE平分∠ABC交AD于E,BC=8㎝,CD=6㎝, ∠D=60°,则下列说法中错误的是( )
∠C=120° B. AE=6 ㎝
C. AD=8 ㎝ D. ∠BED=140 °
A
B
C
D
E
D
A
B
C
D
如图, ABCD的周长是24 ㎝,对角线AC把它分成两个周长为17 ㎝的三角形,则对角线AC的长为( )
A、4 ㎝ B、5 ㎝
C、7 ㎝ D、8 ㎝
B
A
B
C
D
A
B
C
D
如图,在 ABCD中,AB=6 ㎝,BC=8 ㎝,
∠B=30°,则 ABCD的面积为( )
A、48 ㎝2 B、14 ㎝2
C、24 ㎝2 D、12 ㎝2
A
B
C
D
C
A
B
C
D
如图, ABCD中,AE BC,AF CD, ∠B=60°
BE=2,DF=3。则 ABCD的周长为( )
A、20 B、12
C、20 D、12
A
B
C
D
E
F
C
如图,在 ABCD中,AC=4 ㎝ ,CD=3 ㎝ ,BC=5 ㎝ ,则
ABCD的面积为 ________ .
A
D
C
B
4
5
3
12㎝2
如图, ABCD中,AB=8㎝,BC=6㎝,∠A=30°,点P从点A 出发沿AB以每秒1厘米的速度向点B移动。
(1)当P点运动了几秒时,△PBC为等腰三角形;
(2)设△PBC的面积为y,请写出y关于点P的运动时间t的函数关系式,并写出t的取值范围;
(3)是否存在一点P,使S△PBC= S ABCD?
A
B
C
D
P
8-t
t
6
E
)
30°
)
30°
作 业
全效学习63-64
(当堂测评、分层作业)
