19.1.1 平行四边形的性质2
文档属性
| 名称 | 19.1.1 平行四边形的性质2 |

|
|
| 格式 | zip | ||
| 文件大小 | 575.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-16 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
平行四边形的性质(2)
◆ 上节课我们掌握了平行四边形的哪些性质?
◆什么是平行四边形?
(1) 对边平行且相等.
对角相等.
对角线互相平分.
2.平行四边形的性质:
1.平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
比 一 比
2、 的周长是20,已知AB=6,则
BC=__,CD=__.
1、判断正误:平行线间的线段相等. ( )
4
ABCD
6
3、 中,∠A比∠B大 30 , 则
∠A=__,∠D=__.
ABCD
4、若A、B、C三点不共线,则以这三点为
顶点的平行四边形有__个.
3
105°
75°
运用所学知识解决问题
E
F
H
G
A
B
D
C
运用所学知识解决问题
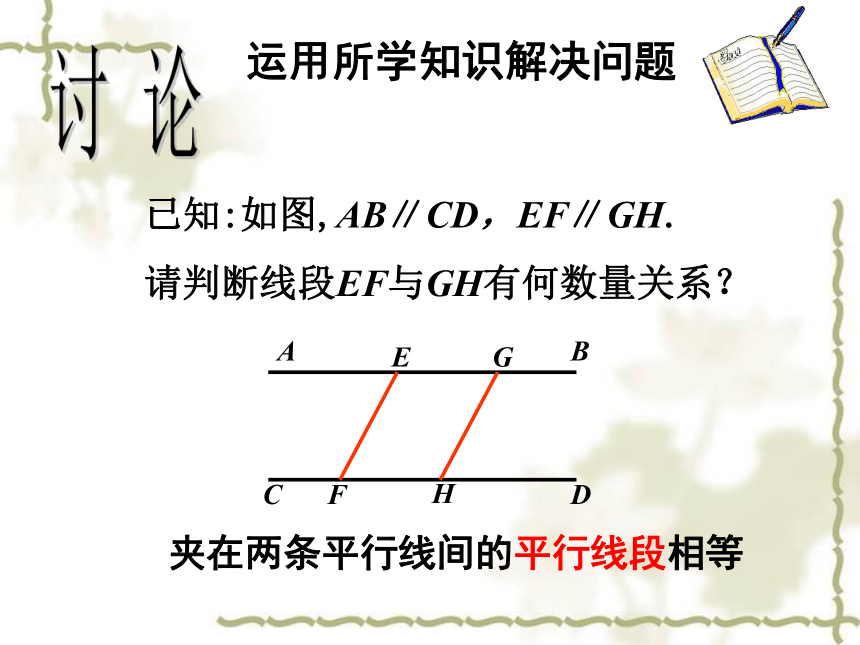
已知:如图,AB∥CD,EF∥GH.
请判断线段EF与GH有何数量关系?
夹在两条平行线间的平行线段相等
A
B
C
D
O
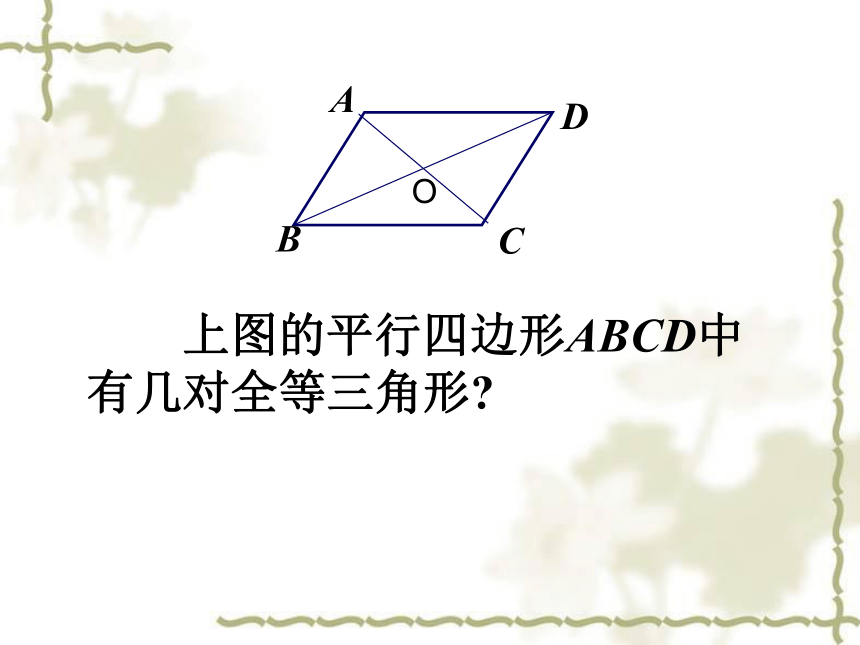
上图的平行四边形ABCD中有几对全等三角形
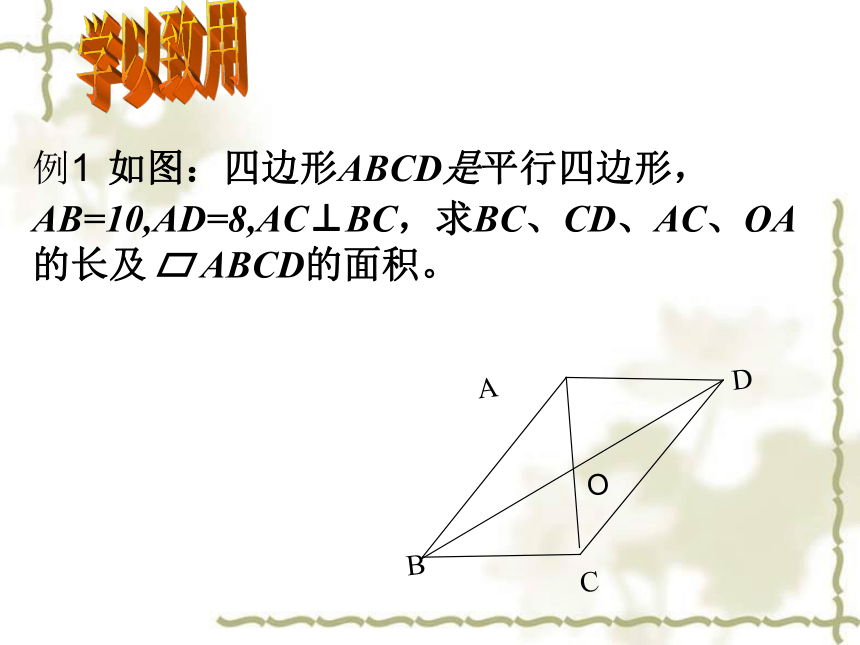
例1 如图:四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长及 ABCD的面积。
A
D
B
C
O
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
当四个孩子看到后,三个弟弟都抢着说应该把这四块地中最大的一块给对家里贡献最大的大哥,同学们,你认为他们能做到吗?为什么呢?
A
C
D
B
o
●
M
ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
3
4
探究一
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
●
●
●
●
在上述问题中,若将直线 EF绕点O旋转至下图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
O
D
C
B
A
E
F
(4)
M
N
●
●
●
●
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。
AC=38mm,BC=24mm,OD=18mm,
求△OBC的周长.
C
B
A
O
D
X
有没有这样的平行四边形,
它的两条对角线长分别为14cm和20cm,
它的一边长为18cm 为什么
例2 已知:如图,在 中,AC与BD相交于点O
ABCD
探究二
练习:5、如图, ABCD的对角线AC,BD相交于点O。已知AB=5cm,△AOB的周长和△BOC的周长相差3cm,则AD的长为__________
2cm或8cm
O
基础训练31、32.
平行四边形的性质(2)
◆ 上节课我们掌握了平行四边形的哪些性质?
◆什么是平行四边形?
(1) 对边平行且相等.
对角相等.
对角线互相平分.
2.平行四边形的性质:
1.平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
比 一 比
2、 的周长是20,已知AB=6,则
BC=__,CD=__.
1、判断正误:平行线间的线段相等. ( )
4
ABCD
6
3、 中,∠A比∠B大 30 , 则
∠A=__,∠D=__.
ABCD
4、若A、B、C三点不共线,则以这三点为
顶点的平行四边形有__个.
3
105°
75°
运用所学知识解决问题
E
F
H
G
A
B
D
C
运用所学知识解决问题
已知:如图,AB∥CD,EF∥GH.
请判断线段EF与GH有何数量关系?
夹在两条平行线间的平行线段相等
A
B
C
D
O
上图的平行四边形ABCD中有几对全等三角形
例1 如图:四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长及 ABCD的面积。
A
D
B
C
O
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
当四个孩子看到后,三个弟弟都抢着说应该把这四块地中最大的一块给对家里贡献最大的大哥,同学们,你认为他们能做到吗?为什么呢?
A
C
D
B
o
●
M
ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
3
4
探究一
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
●
●
●
●
在上述问题中,若将直线 EF绕点O旋转至下图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
O
D
C
B
A
E
F
(4)
M
N
●
●
●
●
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。
AC=38mm,BC=24mm,OD=18mm,
求△OBC的周长.
C
B
A
O
D
X
有没有这样的平行四边形,
它的两条对角线长分别为14cm和20cm,
它的一边长为18cm 为什么
例2 已知:如图,在 中,AC与BD相交于点O
ABCD
探究二
练习:5、如图, ABCD的对角线AC,BD相交于点O。已知AB=5cm,△AOB的周长和△BOC的周长相差3cm,则AD的长为__________
2cm或8cm
O
基础训练31、32.
