4.5 利用三角形全等测距离 课件(14张)
文档属性
| 名称 | 4.5 利用三角形全等测距离 课件(14张) |  | |
| 格式 | pptx | ||
| 文件大小 | 562.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 16:57:39 | ||
图片预览





文档简介
5 利用三角形全等测距离
1. 什么是全等三角形?
2. 我们已经学过了哪几种判定两个三角形全等的方法?
能够完全重合的两个三角形叫做全等三角形.
边边边(SSS),角边 角(ASA),角角边(AAS),边角边(SAS).
3. 两个全等的三角形有哪些性质?
(1) 全等三角形的对应边相等;
(2) 全等三角形的对应角相等.
这位聪明的八路军战士的方法如下:
步测距离
碉堡距离
智慧炸碉堡的故事
从战士的作法中你能发现哪些相等的量?
你知道用什么方法证明哪两个三角形全等吗?
C
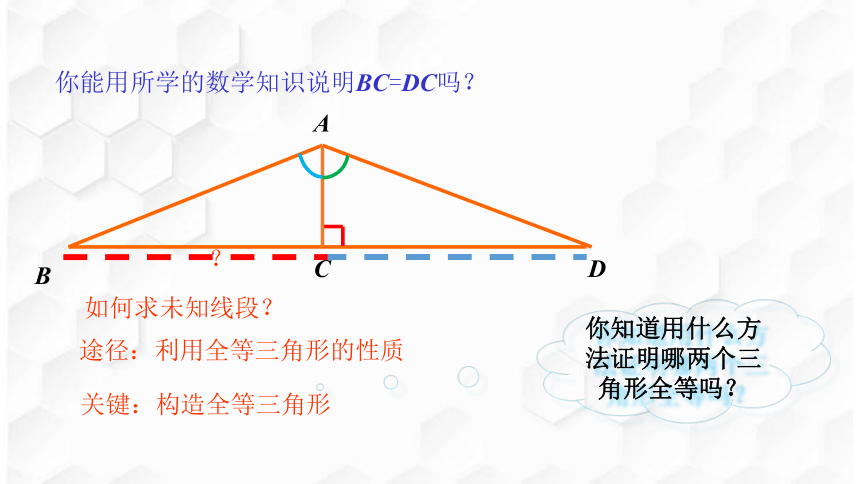
你能用所学的数学知识说明BC=DC吗?
A
B
D
?
如何求未知线段?
途径:利用全等三角形的性质
关键:构造全等三角形
如图所示,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离但绳子不够长,一个叔叔帮他出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是AB间的距离.
你能说明其中的道理吗?
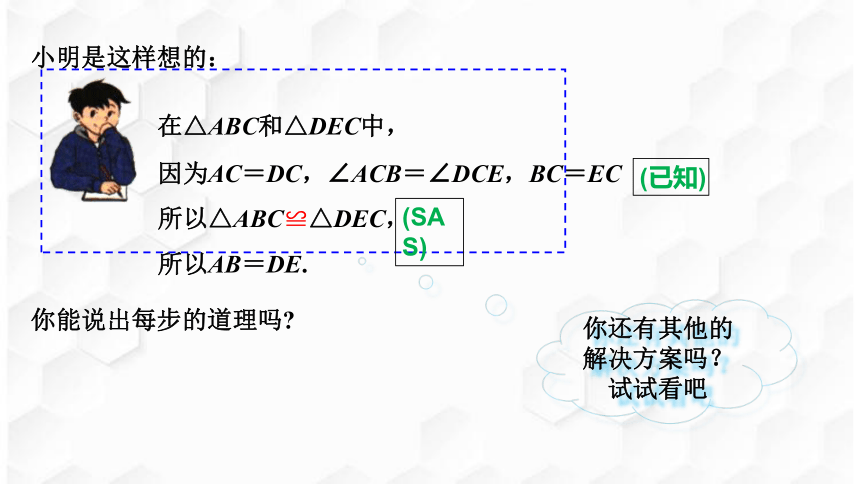
小明是这样想的:
在△ABC和△DEC中,
因为AC=DC,∠ACB=∠DCE,BC=EC
所以△ABC≌△DEC,
所以AB=DE.
你能说出每步的道理吗?
(已知)
(SAS)
你还有其他的解决方案吗?试试看吧
A
·
·
C
D
E
·
1.已知条件是什么?结论又是什么?
2.你能说明设计出方案的理由吗?
在△ABC与△DEC中,已知:AB⊥BE,DE⊥BE,BE=EC,结论:AB=DE.
ASA
方案一:
B
方案二:
1
2
B
C
D
A
1.已知条件是什么?结论又是什么?
在△ABC与△DEC中,已知:AD//BC,AD=BC,结论:AB=DC.
2.你能说明设计出方案的理由吗?
SAS
B
A
D
C
方案三:
1.已知条件是什么?结论又是什么?
在△ABC与△DEC中,已知:AD⊥BD,AD=DC,结论:AB=BC.
2.你能说明设计出方案的理由吗?
SAS
1.如图,将两根钢条AA′,BB′的中点O连在一起,使
AA′,BB′可以绕着点O自由转动,就做成了一个测量
工件,由三角形全等得出A′B′的长等于内槽宽AB,那
么判定△OAB≌△OA′B′的理由是( )
A.边角边 B.角边角
C.边边边 D.角角边
A
2.如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长.判定△EDC≌△ABC的理由是( )
A.SSS B.ASA C.AAS D.SAS
B
A
●
●
D
C
E
F
B
3.如图所示,已知AC=DB,AO=DO,CD=100 m,则A,B两点间的距离( )
A.大于100 m B.等于100 m
C.小于100 m D.无法确定
C
小结
1.知识:
利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
2.方法:
(1)延长法构造全等三角形;
(2)垂直法构造全等三角形.
3.数学思想:
树立用三角形全等构建数学模型解决实际问题的思想.
谢 谢 观 看!
1. 什么是全等三角形?
2. 我们已经学过了哪几种判定两个三角形全等的方法?
能够完全重合的两个三角形叫做全等三角形.
边边边(SSS),角边 角(ASA),角角边(AAS),边角边(SAS).
3. 两个全等的三角形有哪些性质?
(1) 全等三角形的对应边相等;
(2) 全等三角形的对应角相等.
这位聪明的八路军战士的方法如下:
步测距离
碉堡距离
智慧炸碉堡的故事
从战士的作法中你能发现哪些相等的量?
你知道用什么方法证明哪两个三角形全等吗?
C
你能用所学的数学知识说明BC=DC吗?
A
B
D
?
如何求未知线段?
途径:利用全等三角形的性质
关键:构造全等三角形
如图所示,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离但绳子不够长,一个叔叔帮他出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是AB间的距离.
你能说明其中的道理吗?
小明是这样想的:
在△ABC和△DEC中,
因为AC=DC,∠ACB=∠DCE,BC=EC
所以△ABC≌△DEC,
所以AB=DE.
你能说出每步的道理吗?
(已知)
(SAS)
你还有其他的解决方案吗?试试看吧
A
·
·
C
D
E
·
1.已知条件是什么?结论又是什么?
2.你能说明设计出方案的理由吗?
在△ABC与△DEC中,已知:AB⊥BE,DE⊥BE,BE=EC,结论:AB=DE.
ASA
方案一:
B
方案二:
1
2
B
C
D
A
1.已知条件是什么?结论又是什么?
在△ABC与△DEC中,已知:AD//BC,AD=BC,结论:AB=DC.
2.你能说明设计出方案的理由吗?
SAS
B
A
D
C
方案三:
1.已知条件是什么?结论又是什么?
在△ABC与△DEC中,已知:AD⊥BD,AD=DC,结论:AB=BC.
2.你能说明设计出方案的理由吗?
SAS
1.如图,将两根钢条AA′,BB′的中点O连在一起,使
AA′,BB′可以绕着点O自由转动,就做成了一个测量
工件,由三角形全等得出A′B′的长等于内槽宽AB,那
么判定△OAB≌△OA′B′的理由是( )
A.边角边 B.角边角
C.边边边 D.角角边
A
2.如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长.判定△EDC≌△ABC的理由是( )
A.SSS B.ASA C.AAS D.SAS
B
A
●
●
D
C
E
F
B
3.如图所示,已知AC=DB,AO=DO,CD=100 m,则A,B两点间的距离( )
A.大于100 m B.等于100 m
C.小于100 m D.无法确定
C
小结
1.知识:
利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
2.方法:
(1)延长法构造全等三角形;
(2)垂直法构造全等三角形.
3.数学思想:
树立用三角形全等构建数学模型解决实际问题的思想.
谢 谢 观 看!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
