4.5 利用三角形全等测距离 课件(16张)
文档属性
| 名称 | 4.5 利用三角形全等测距离 课件(16张) |  | |
| 格式 | pptx | ||
| 文件大小 | 349.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 16:57:39 | ||
图片预览






文档简介
4.5
利用三角形全等测距离
●复习:
1、判定两个三角形全等有哪几种方法?
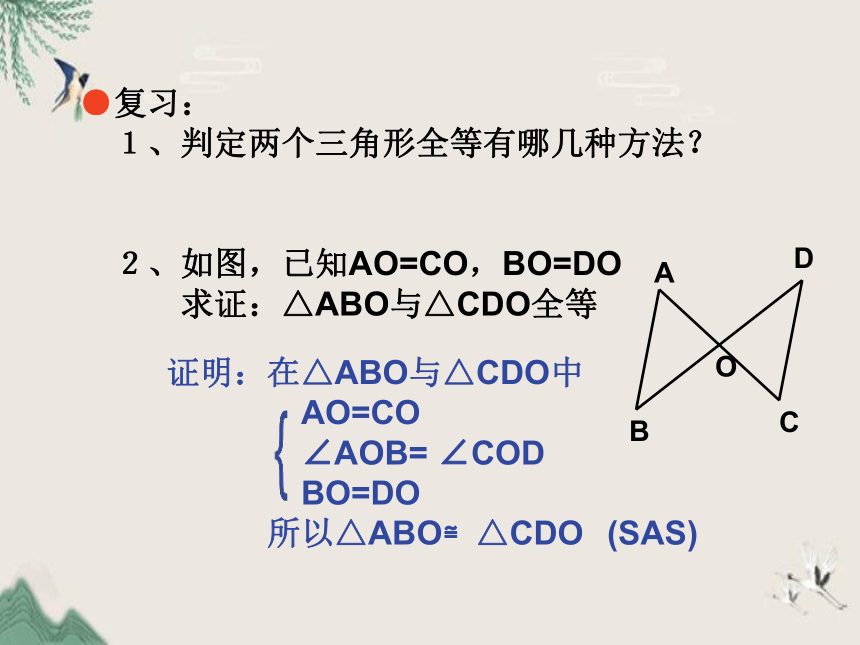
2、如图,已知AO=CO,BO=DO
求证:△ABO与△CDO全等
A
B
C
D
O
(SAS)
证明:在△ABO与△CDO中
AO=CO
∠AOB= ∠COD
BO=DO
所以△ABO≌△CDO
通过前一阶段的学习我们知道了如何判定三角形全等和画全等三角形,这节课将用三角形全等的条件来解决一些问题.
下面是一位经历过战争的老人讲述的一个故事:
在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,如何估测这个距离呢?
●提出问题:
一位战士想出来这样一个办法:他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部
↓然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上.
↓接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.
你能解释其中的道理吗?
●学习目标:
知识与技能:
1、能利用三角形的全等解决实际问题,体会数学与实际生活的联系。
2、能在解决问题的过程中进行有条理的思考和表达。
过程与方法:
1、通过利用三角形全等解决实际问题,感受所学知识与实际生活的联系。
2、在解决问题的过程中逐步学会有条理地思考和表达。
情感、态度与价值观:
敢于面对数学活动中的困难,并有独立克服困难和运用知识解决问题的成功经验,有学好数学的信心。
●重点:
利用三角形全等解决实际问题
●难点:
在解决问题过程中进行有条理的思考与表达
A
B
D
C
1
2
步测距离
碉堡距离
?
解:在△ADB与△ADC中
∠__=∠__
AD=AD
∠_____=∠_____=90°
∴△ADB≌△ADC (_______)
∴DB=DC
●例:如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长。他叔叔帮他出了这样的一个主意:
先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度。
(1)请结合问题列出所有的已知条件;
(2)DE=AB吗,请说明理由。
·
·
A
B
● 练习:
1、有一座锥形小山,如图,要测量锥形小山两端A、B的距离,先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离,你能说说其中的道理吗?
A
B
E
D
C
思路点拨:
(1)找到题目中所有的已知条件
(2)证明两个三角形全等
● 练习:
2、在一座楼相邻两面墙的外部有两点A、C,如图,请设计方案测量A、C两点间的距离
A
C
B
E
D
● 能力提升:
● 扩展应用:
某地质勘测队在对某地进行实地勘测途中,被一条波涛汹涌的大河拦住了去路,现在他们手中只有一架测角器和足够长的米尺,你能帮他们不过河测量出这条河的宽度吗?
●课堂小结 检测自己今天的学习成果:
1、 在遇到不可直接测量的距离时,我们可以通过构造_________,使“不可直接测量的距离”变成“__________”
2、 在不能直接测量两点距离时,需要构造全等三角形进行测量,构造全等三角形的第一步是选取能够直接到达这两点的一个点,以下四幅图点B的位置选取正确的是:(点A、点C所以的是两堵墙)
3、 利用全等三角形的知识将不能直接测量距离的问题转化为可以直接测量的距离问题 叫做数学建模,其基本方法是结合“数形”的已知条件抽象几何图形。
作业:
必做题 课本175页知识技能1
选做题 课本175页数学理解1
·
·
A
B
C
D
E
·
·
A
B
C
D
E
·
·
A
B
C
D
E
再 见
利用三角形全等测距离
●复习:
1、判定两个三角形全等有哪几种方法?
2、如图,已知AO=CO,BO=DO
求证:△ABO与△CDO全等
A
B
C
D
O
(SAS)
证明:在△ABO与△CDO中
AO=CO
∠AOB= ∠COD
BO=DO
所以△ABO≌△CDO
通过前一阶段的学习我们知道了如何判定三角形全等和画全等三角形,这节课将用三角形全等的条件来解决一些问题.
下面是一位经历过战争的老人讲述的一个故事:
在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,如何估测这个距离呢?
●提出问题:
一位战士想出来这样一个办法:他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部
↓然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上.
↓接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.
你能解释其中的道理吗?
●学习目标:
知识与技能:
1、能利用三角形的全等解决实际问题,体会数学与实际生活的联系。
2、能在解决问题的过程中进行有条理的思考和表达。
过程与方法:
1、通过利用三角形全等解决实际问题,感受所学知识与实际生活的联系。
2、在解决问题的过程中逐步学会有条理地思考和表达。
情感、态度与价值观:
敢于面对数学活动中的困难,并有独立克服困难和运用知识解决问题的成功经验,有学好数学的信心。
●重点:
利用三角形全等解决实际问题
●难点:
在解决问题过程中进行有条理的思考与表达
A
B
D
C
1
2
步测距离
碉堡距离
?
解:在△ADB与△ADC中
∠__=∠__
AD=AD
∠_____=∠_____=90°
∴△ADB≌△ADC (_______)
∴DB=DC
●例:如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长。他叔叔帮他出了这样的一个主意:
先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度。
(1)请结合问题列出所有的已知条件;
(2)DE=AB吗,请说明理由。
·
·
A
B
● 练习:
1、有一座锥形小山,如图,要测量锥形小山两端A、B的距离,先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离,你能说说其中的道理吗?
A
B
E
D
C
思路点拨:
(1)找到题目中所有的已知条件
(2)证明两个三角形全等
● 练习:
2、在一座楼相邻两面墙的外部有两点A、C,如图,请设计方案测量A、C两点间的距离
A
C
B
E
D
● 能力提升:
● 扩展应用:
某地质勘测队在对某地进行实地勘测途中,被一条波涛汹涌的大河拦住了去路,现在他们手中只有一架测角器和足够长的米尺,你能帮他们不过河测量出这条河的宽度吗?
●课堂小结 检测自己今天的学习成果:
1、 在遇到不可直接测量的距离时,我们可以通过构造_________,使“不可直接测量的距离”变成“__________”
2、 在不能直接测量两点距离时,需要构造全等三角形进行测量,构造全等三角形的第一步是选取能够直接到达这两点的一个点,以下四幅图点B的位置选取正确的是:(点A、点C所以的是两堵墙)
3、 利用全等三角形的知识将不能直接测量距离的问题转化为可以直接测量的距离问题 叫做数学建模,其基本方法是结合“数形”的已知条件抽象几何图形。
作业:
必做题 课本175页知识技能1
选做题 课本175页数学理解1
·
·
A
B
C
D
E
·
·
A
B
C
D
E
·
·
A
B
C
D
E
再 见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
