5.2 探索轴对称的性质 课件(24张)
文档属性
| 名称 | 5.2 探索轴对称的性质 课件(24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 416.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 00:00:00 | ||
图片预览



文档简介
第五章 生活中的轴对称
探索轴对称的性质
教学目标
1、理解轴对称和轴对称图形的概念和含义;
2、会画轴对称图形的对称轴,并能判断一个图形是否是轴对称图形;
3、理解并掌握轴对称的基本性质;
4、知道轴对称图形的画法,会作已知图形的轴对称图形.
新课导入
1、如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做 , 这条直线叫这个图形的 .
2、对于两个图形,把一个图形沿着某一条直线对折,如果它能够与另一个图形完全重合,那么就说 , 这条直线就是 .
轴对称图形
对称轴
对称轴
这两个图形成轴对称
回顾旧知
新课导入
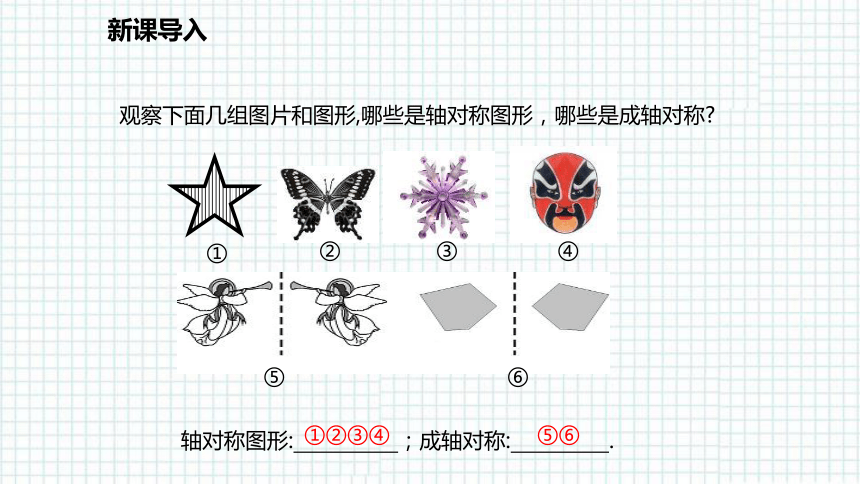
观察下面几组图片和图形,哪些是轴对称图形,哪些是成轴对称?
轴对称图形: ;成轴对称: .
①
②
③
④
⑤
⑥
①②③④ ⑤⑥
新知探究
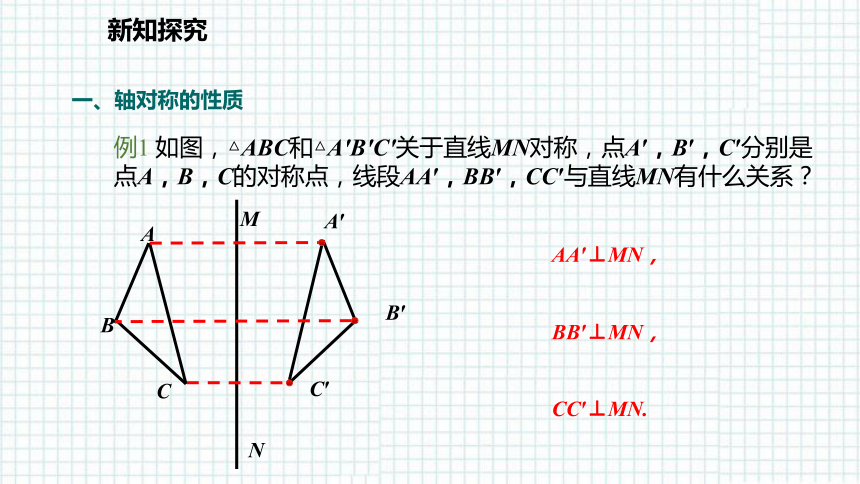
例1 如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
一、轴对称的性质
新知探究
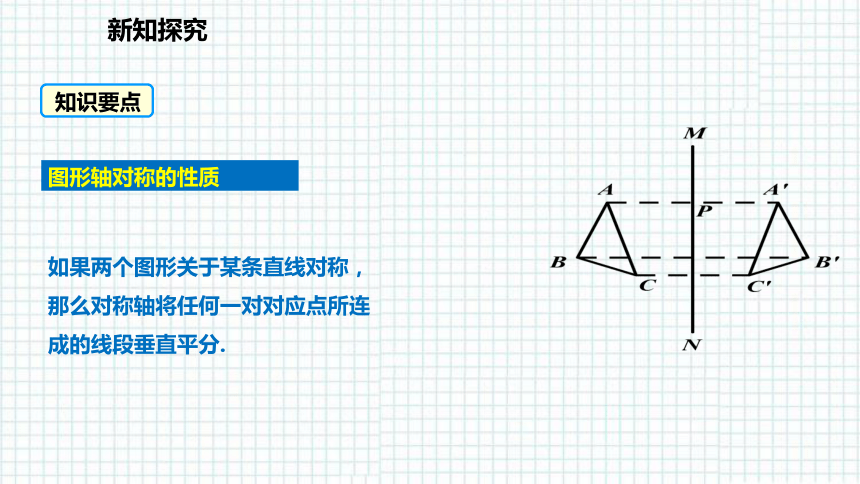
如果两个图形关于某条直线对称,
那么对称轴将任何一对对应点所连
成的线段垂直平分.
知识要点
图形轴对称的性质
新知探究
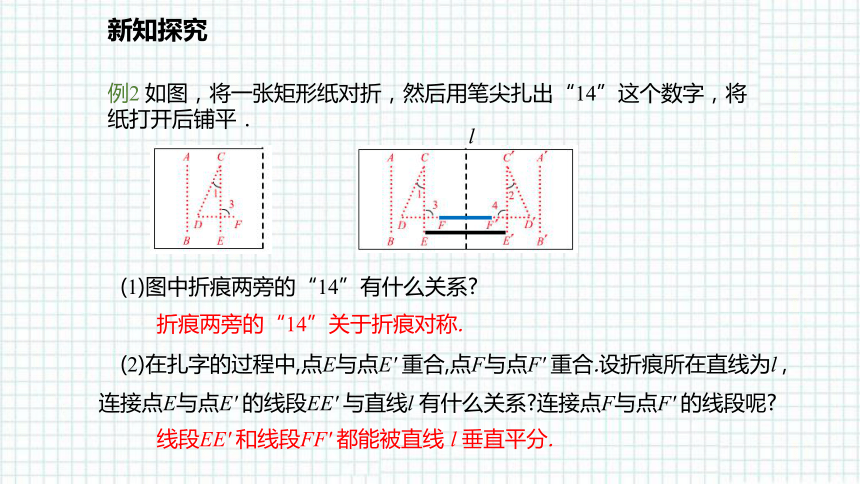
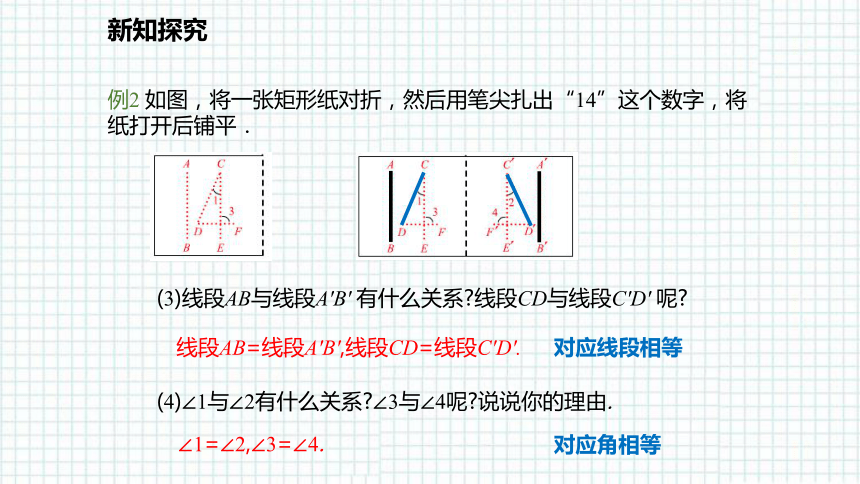
例2 如图,将一张矩形纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平.
(1)图中折痕两旁的“14”有什么关系?
(2)在扎字的过程中,点E与点E' 重合,点F与点F' 重合.设折痕所在直线为l ,连接点E与点E' 的线段EE' 与直线l 有什么关系?连接点F与点F' 的线段呢?
折痕两旁的“14”关于折痕对称.
线段EE' 和线段FF' 都能被直线 l 垂直平分.
l
新知探究
(3)线段AB与线段A'B' 有什么关系?线段CD与线段C'D' 呢?
(4)∠1与∠2有什么关系?∠3与∠4呢?说说你的理由.
∠1=∠2,∠3=∠4.
线段AB=线段A'B',线段CD=线段C'D'.
例2 如图,将一张矩形纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平.
对应线段相等
对应角相等
新知探究
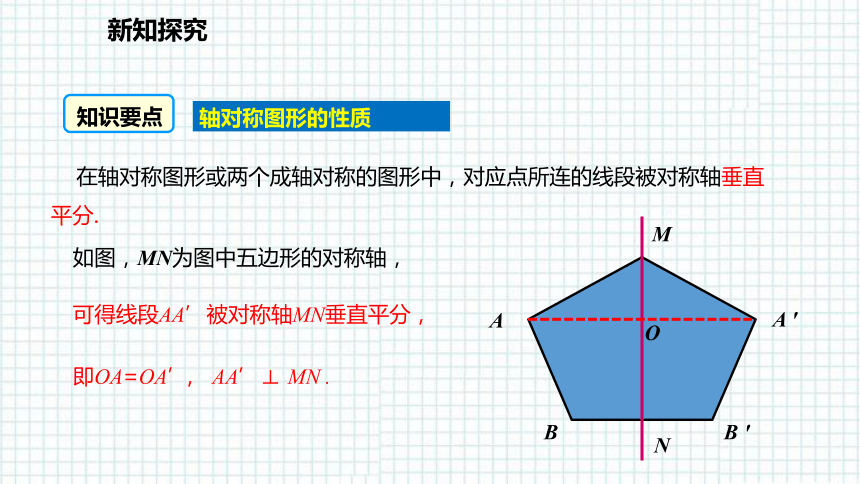
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分.
知识要点
轴对称图形的性质
A
B
A ′
B ′
M
N
如图,MN为图中五边形的对称轴,
可得线段AA’被对称轴MN垂直平分,
即OA=OA’, AA’⊥ MN .
O
新知探究
归纳总结
在轴对称图形或两个成轴对称的图形中:
1.对应点所连的线段被对称轴垂直平分;
2.对应线段相等;
3.对应角相等.
新知探究
问题1:如何画一个点的轴对称图形?
画出点P关于直线l的对称点P′.
﹒
l
P
﹒
P′
O
作法:
(1)过点P作l的垂线,垂足为点O;
(2)在垂线上截取OP′=OP,
点P′就是点P关于直线l的对称点.
互动探究
二、作轴对称图形
∟
新知探究
问题2:如何画一条线段的对称图形?
已知线段AB,画出线段AB关于直线l的对称线段.
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A ′
A ′
A ′
B ′
(B ′)
B ′
新知探究
想一想:如果有一个图形和一条直线,如何画出与这个图形关于这条直线对称的图形呢?
例3 如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
A
B
C
分析:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
新知探究
作法:(1)过点A画直线l的垂线,垂足
为点O,在垂线上截取OA′=OA,
A′就是点A关于直线l的对称点;
(3)连接A′B′,B′C′,C′A′,得
到△ A′B′C′即为所求.
(2)同理,分别画出点B,C关
于直线l的对称点B′,C′ ;
A
B
C
A′
B′
C′
O
∟
新知探究
方法归纳
作轴对称图形的方法
几何图形都可以看作由点组成.对于某些图形,只要作出图形
中一些特殊点(如线段端点)的对称点,连接这些对称点,就可
以得到原图形的轴对称图形.
新知探究
例4 在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.
方法归纳:作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.
A
B
C
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
新知探究
1、如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130° B.150°
C.40° D.65°
典例精析
方法归纳:轴对称是一种全等变换,在轴对称图形中求角度时,一般先根据轴对称的性质及已知条件,得出相关角的度数,然后再结合多边形的内角和或三角形的性质求解.
A
新知探究
2、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
A.4cm2
B.8cm2
C.12cm2
D.16cm2
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积
的一半.因为正方形ABCD的边长为4cm,所以S阴影=42÷2=8(cm2).
B
课堂小结
轴对称的性质
1.对应点所连线段被对称轴垂直平分,
2.对应线段相等,
3.对应角相等
画轴对称图形
作图原理
作图方法
对称轴垂直平分对应点所连的线段
1.找特征点;
2.作垂线;
3.截取等长;
4.依次连线
课堂小测
1. 作已知点关于某直线的对称点的第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
B
2.如图,把下列图形补成关于直线 l 的对称图形.
课堂小测
课堂小测
3.如图,△ABC与△DEF关于直线MN对称,则下列结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.AD的连线被直线MN垂直平分
A
4.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上点A′处,折痕为CD,则∠A′DB的度数为_______.
10°
A
B
A’
C
D
课堂小测
5. 如图给出了一个图案的一半,虚线 l 是这个图案的对称轴.整个图案是个什么形状?请准确地画出它的另一半.
B
A
C
D
E
F
G
H
l
如图,整个图案是一个类似房子的形状.
再 见
探索轴对称的性质
教学目标
1、理解轴对称和轴对称图形的概念和含义;
2、会画轴对称图形的对称轴,并能判断一个图形是否是轴对称图形;
3、理解并掌握轴对称的基本性质;
4、知道轴对称图形的画法,会作已知图形的轴对称图形.
新课导入
1、如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做 , 这条直线叫这个图形的 .
2、对于两个图形,把一个图形沿着某一条直线对折,如果它能够与另一个图形完全重合,那么就说 , 这条直线就是 .
轴对称图形
对称轴
对称轴
这两个图形成轴对称
回顾旧知
新课导入
观察下面几组图片和图形,哪些是轴对称图形,哪些是成轴对称?
轴对称图形: ;成轴对称: .
①
②
③
④
⑤
⑥
①②③④ ⑤⑥
新知探究
例1 如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
一、轴对称的性质
新知探究
如果两个图形关于某条直线对称,
那么对称轴将任何一对对应点所连
成的线段垂直平分.
知识要点
图形轴对称的性质
新知探究
例2 如图,将一张矩形纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平.
(1)图中折痕两旁的“14”有什么关系?
(2)在扎字的过程中,点E与点E' 重合,点F与点F' 重合.设折痕所在直线为l ,连接点E与点E' 的线段EE' 与直线l 有什么关系?连接点F与点F' 的线段呢?
折痕两旁的“14”关于折痕对称.
线段EE' 和线段FF' 都能被直线 l 垂直平分.
l
新知探究
(3)线段AB与线段A'B' 有什么关系?线段CD与线段C'D' 呢?
(4)∠1与∠2有什么关系?∠3与∠4呢?说说你的理由.
∠1=∠2,∠3=∠4.
线段AB=线段A'B',线段CD=线段C'D'.
例2 如图,将一张矩形纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平.
对应线段相等
对应角相等
新知探究
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分.
知识要点
轴对称图形的性质
A
B
A ′
B ′
M
N
如图,MN为图中五边形的对称轴,
可得线段AA’被对称轴MN垂直平分,
即OA=OA’, AA’⊥ MN .
O
新知探究
归纳总结
在轴对称图形或两个成轴对称的图形中:
1.对应点所连的线段被对称轴垂直平分;
2.对应线段相等;
3.对应角相等.
新知探究
问题1:如何画一个点的轴对称图形?
画出点P关于直线l的对称点P′.
﹒
l
P
﹒
P′
O
作法:
(1)过点P作l的垂线,垂足为点O;
(2)在垂线上截取OP′=OP,
点P′就是点P关于直线l的对称点.
互动探究
二、作轴对称图形
∟
新知探究
问题2:如何画一条线段的对称图形?
已知线段AB,画出线段AB关于直线l的对称线段.
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A ′
A ′
A ′
B ′
(B ′)
B ′
新知探究
想一想:如果有一个图形和一条直线,如何画出与这个图形关于这条直线对称的图形呢?
例3 如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
A
B
C
分析:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
新知探究
作法:(1)过点A画直线l的垂线,垂足
为点O,在垂线上截取OA′=OA,
A′就是点A关于直线l的对称点;
(3)连接A′B′,B′C′,C′A′,得
到△ A′B′C′即为所求.
(2)同理,分别画出点B,C关
于直线l的对称点B′,C′ ;
A
B
C
A′
B′
C′
O
∟
新知探究
方法归纳
作轴对称图形的方法
几何图形都可以看作由点组成.对于某些图形,只要作出图形
中一些特殊点(如线段端点)的对称点,连接这些对称点,就可
以得到原图形的轴对称图形.
新知探究
例4 在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.
方法归纳:作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.
A
B
C
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
新知探究
1、如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130° B.150°
C.40° D.65°
典例精析
方法归纳:轴对称是一种全等变换,在轴对称图形中求角度时,一般先根据轴对称的性质及已知条件,得出相关角的度数,然后再结合多边形的内角和或三角形的性质求解.
A
新知探究
2、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
A.4cm2
B.8cm2
C.12cm2
D.16cm2
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积
的一半.因为正方形ABCD的边长为4cm,所以S阴影=42÷2=8(cm2).
B
课堂小结
轴对称的性质
1.对应点所连线段被对称轴垂直平分,
2.对应线段相等,
3.对应角相等
画轴对称图形
作图原理
作图方法
对称轴垂直平分对应点所连的线段
1.找特征点;
2.作垂线;
3.截取等长;
4.依次连线
课堂小测
1. 作已知点关于某直线的对称点的第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
B
2.如图,把下列图形补成关于直线 l 的对称图形.
课堂小测
课堂小测
3.如图,△ABC与△DEF关于直线MN对称,则下列结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.AD的连线被直线MN垂直平分
A
4.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上点A′处,折痕为CD,则∠A′DB的度数为_______.
10°
A
B
A’
C
D
课堂小测
5. 如图给出了一个图案的一半,虚线 l 是这个图案的对称轴.整个图案是个什么形状?请准确地画出它的另一半.
B
A
C
D
E
F
G
H
l
如图,整个图案是一个类似房子的形状.
再 见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
