人教A版数学2019选修第二册综合练习附答案第5章一元函数的导数及其应用(Word含解析)
文档属性
| 名称 | 人教A版数学2019选修第二册综合练习附答案第5章一元函数的导数及其应用(Word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 168.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 18:18:03 | ||
图片预览




文档简介
选修第二册第5章一元函数的导数及其应
一、选择题
函数
在区间
上的平均变化率为
A.
B.
C.
D.
下列导数运算正确的是
A.
B.
C.
D.
,若
,则
等于
A.
B.
C.
D.
函数
在
上可导,且
,则
A.
B.
C.
D.不确定
已知函数
,则
,,
的大小关系是
A.
B.
C.
D.
函数
的图象大致为
A.B.
C.D.
已知函数
,直线
与曲线
相切,则
A.
B.
C.
D.
设函数
,当
时,不等式
对任意的
恒成立,则
的可能取值是
A.
B.
C.
D.
二、填空题
已知
,则
.
已知
是定义在
上的奇函数,当
时,,则
;曲线
在点
处的切线方程为
.
已知函数
在
上单调递减,则
的取值范围是
.
已知函数
,若存在
,使得
,则
的取值范围是
.
三、解答题
已知函数
.
(1)
求函数
的单调区间;
(2)
求函数
在区间
上的值域.
已知函数
.
(1)
若曲线
在点
处的切线与
轴平行,且
,求
,
的值;
(2)
若
,
对任意
恒成立,求
的取值范围.
已知函数
.
(1)
若
,求
的极值;
(2)
证明:当
时,.
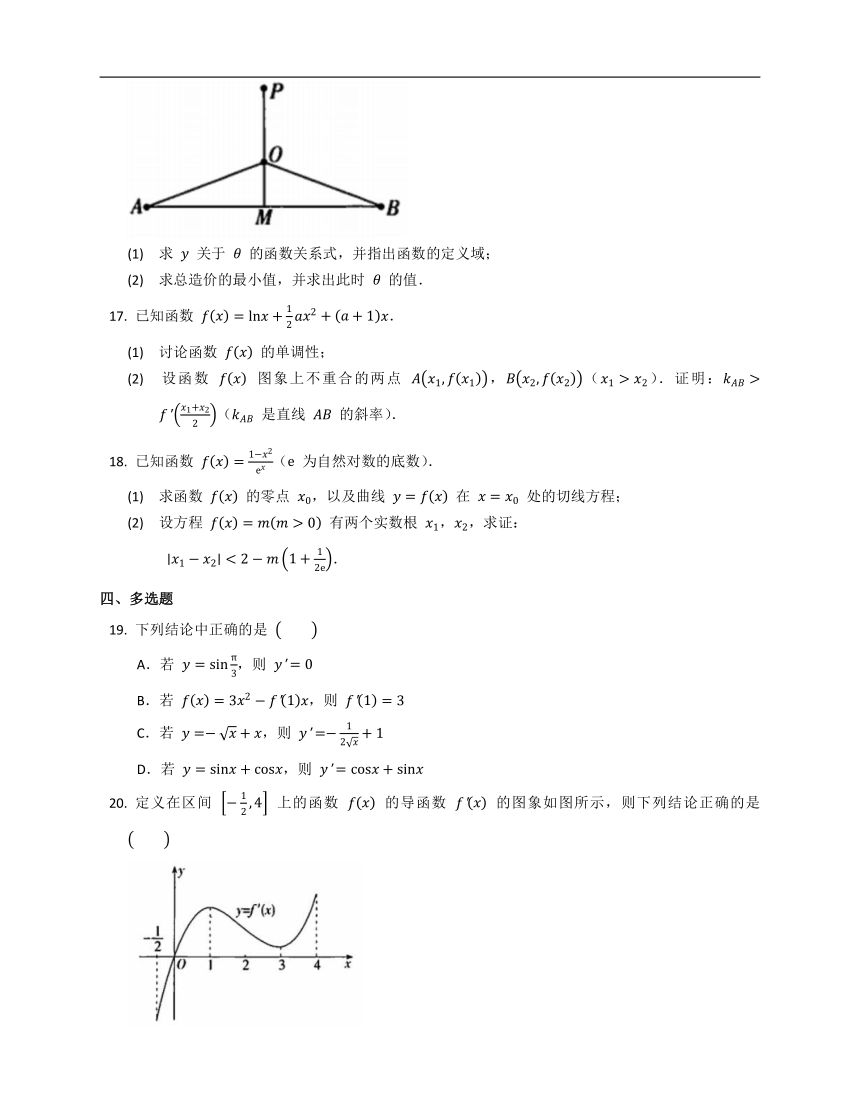
如图,已知
,
两个城镇相距
千米,设
是
的中点,在
的中垂线上有一高铁站
,,
的距离为
千米.为方便居民出行,在线段
上任取一点
(点
不与
,
重合)建设交通枢纽,从高铁站铺设快速路到
处,再铺设快速路分别到
,
两处.因地质条件等各种因素,其中快速路
造价为
百万元/千米,快速路
造价为
百万元/千米,快速路
造价为
百万元/千米.设
,总造价为
(单位:百万元).
(1)
求
关于
的函数关系式,并指出函数的定义域;
(2)
求总造价的最小值,并求出此时
的值.
已知函数
.
(1)
讨论函数
的单调性;
(2)
设函数
图象上不重合的两点
,().证明:(
是直线
的斜率).
已知函数
(
为自然对数的底数).
(1)
求函数
的零点
,以及曲线
在
处的切线方程;
(2)
设方程
有两个实数根
,,求证:
.
四、多选题
下列结论中正确的是
A.若
,则
B.若
,则
C.若
,则
D.若
,则
定义在区间
上的函数
的导函数
的图象如图所示,则下列结论正确的是
A.函数
在区间
上单调递增
B.函数
在区间
上单调递减
C.函数
在
处取得极大值
D.函数
在
处取得极小值
若实数
的取值使函数
在定义域上有两个极值点,则称函数
具有“凹凸趋向性”,已知
是函数
的导数,且
,当函数
具有“凹凸趋向性”时,
的取值范围的子集有
A.
B.
C.
D.
已知定义在
上的函数
的导函数为
,且
,,则下列判断正确的是
A.
B.
C.
D.
答案
一、选择题
1.
【答案】B
【解析】因为
,
所以
在区间
上的平均变化率为
.
故选B.
2.
【答案】B
【解析】对于A,,A错误;
对于B,,B正确;
对于C,,C错误;
对于D,,D错误.
故选B.
3.
【答案】B
【解析】由题得
,
所以
,
所以
,
解得
.
4.
【答案】C
【解析】由
,得
,
所以
,
所以
,
所以
,
所以
,
所以
.
5.
【答案】A
【解析】易知
为偶函数,
所以
,
因为
,当
时,,
所以
在
上为增函数,
所以
,
所以
.
故选A.
6.
【答案】A
【解析】因为
,
所以函数
是偶函数,
所以
的图象关于
轴对称,故排除B.
当
时,,故排除D.
当
时,,,当
时,
取最小值,且
,故排除C.
7.
【答案】B
【解析】设切点为
,由
,得
,
又直线
与曲线
相切,
所以
由②③得
,
代入①得
.
易得
,
代入①得
.
8.
【答案】D
【解析】由
,得
,令
,得
或
,当
时,,
所以
在
,
上单调递减,在
上单调递增,
又当
时,,所以
在
上为减函数,
又
,,所以
,,
由不等式
对任意的
恒成立,得
对任意的
恒成立,
所以
恒成立,
解得
,即
,
结合选项知,
的可能取值是
.
二、填空题
9.
【答案】
【解析】因为
,
所以
10.
【答案】
;
【解析】由
是定义在
上的奇函数知,,
所以
,
所以当
时,,
所以
,
又
,
所以
,
所以
,
所以
,,
所以
在
处的切线方程为
,
即
.
11.
【答案】
【解析】因为函数
在
上单调递减,
所以
在
上恒成立,即
在
上恒成立,
利用导数易知函数
在
上是增函数,
所以
,
故
.
12.
【答案】
【解析】因为
,
所以不妨设
.
当
时,.
当
时,,
根据
可知
,
所以
,,
所以
,
故
,
所以
,.
记
,则
,
于是易得
在
上单调递减,在
上单调递增,
所以
,
又当
时,,
所以
的值域是
.
所以
的取值范围是
.
三、解答题
13.
【答案】
(1)
由题意得,,
令
,得
,
令
,得
或
,
故函数
的单调递增区间为
,
单调递减区间为
,.
(2)
易知
,,,
因为
所以
.(或由
,,
可得
)
又当
时,,
所以函数
在区间
上的值域为
.
14.
【答案】
(1)
由
,得
,
由
得
(2)
因为
,
所以
,
对任意
恒成立等价于
对任意
恒成立,
令
,则
.
当
时,,
所以
在
上单调递减,
当
时,,
所以
在
上单调递增,
所以
,
所以
.
15.
【答案】
(1)
因为
,
所以
,
当
时,;
当
时,,
当
发生变化时,,
的变化情况如下表:因此,当
时,
有极大值,并且极大值为
,没有极小值.
(2)
令
,
则
,
由()知
在
上单调递增,在
上单调递减.
又
,,,
所以
在
上存在唯一零点,设为
,则
,
当
时,;当
时,,
所以
在区间
上单调递增,在区间
上单调递减,
又
,,
所以当
时,,
故
.
16.
【答案】
(1)
因为
,,
为
的中点,
所以
,,,
所以
(2)
设
则
令
,得
,
又
,
所以
.
当
时,,,
单调递减;
当
时,,,
单调递增.
所以
的最小值为
,此时总造价最小.
所以当
时,总造价最小,最小值为
百万元.
17.
【答案】
(1)
由题意得,函数
的定义域为
,且
①当
时,,
此时
在
上单调递增.
②当
时,令
,
得
或
(舍),,
由
得
,
由
得
,
所以
在
上单调递增,
在
上单调递减.
综上,当
时,函数
在
上单调递增;
当
时,函数
在
上单调递增,
在
上单调递减.
(2)
由题意得
,
,
所以
又
,
所以要证
成立,
只需证
成立,
即证
成立.
令
,
即证当
时,
成立.
设
,
则
,
所以函数
在
上是单调递增函数,
所以
,都有
,
即
,都有
,
所以
.
18.
【答案】
(1)
由
,得
,
所以函数
的零点
.
易得
,,,
所以曲线
在
处的切线方程为
.
,,
所以曲线
在
处的切线方程为
.
(2)
由()知
.
令
,得
.
当
时,;
当
时,.
所以
的单调递增区间为
,,
单调递减区间为
.
由()知,当
或
时,;
当
时,.
下面证明:当
时,.
当
时,
.
易知,
在
上单调递增,
所以
对任意
恒成立,
所以当
时,.
由
得
.
记
.
不妨设
,则
,
所以
.
要证
,只需证
,
即证
.
又因为
,
所以只需证
,
即
.
因为
,
所以
,
所以只需证
.
令
,则
.
当
时,,
为单调递减函数;
当
时,,
为单调递增函数.
所以
,
所以
,
所以
.
四、多选题
19.
【答案】A;B;C
【解析】选项A中,若
,则
,故A正确;
选项B中,若
,则
,令
,则
,解得
,故B正确;
选项C中,若
,则
,故C正确;
选项D中,若
,则
,故D错误.
故选ABC.
20.
【答案】A;B;D
【解析】由
的图象知,当
时,;
当
时,,
因此
在
上单调递减,在
上单调递增,故A,B正确.
在
附近单调递增,在
处不取极大值,故C错误.
由
在
上单调递减,在
上单调递增,得
在
处取得极小值,故D正确.
21.
【答案】B;D
【解析】依题意得
,
若函数
具有“凹凸趋向性”,则
在
上有
个不同的实数根,
令
,则
,
令
,解得
,令
,解得
,
所以
在
上单调递减,在
上单调递增,
故
的最小值是
,当
时,,故
.
22.
【答案】C;D
【解析】令
,,
则
,
因为
,
所以
在
上恒成立,
因此函数
在
上单调递减,
因此
,
即
,
即
,
故A错误;
又
,
所以
,
所以
在
上恒成立,
因为
,
所以
,
故B错误;
又
,
所以
,
即
,
故C正确;
又
,
所以
,
即
,
故D正确.
一、选择题
函数
在区间
上的平均变化率为
A.
B.
C.
D.
下列导数运算正确的是
A.
B.
C.
D.
,若
,则
等于
A.
B.
C.
D.
函数
在
上可导,且
,则
A.
B.
C.
D.不确定
已知函数
,则
,,
的大小关系是
A.
B.
C.
D.
函数
的图象大致为
A.B.
C.D.
已知函数
,直线
与曲线
相切,则
A.
B.
C.
D.
设函数
,当
时,不等式
对任意的
恒成立,则
的可能取值是
A.
B.
C.
D.
二、填空题
已知
,则
.
已知
是定义在
上的奇函数,当
时,,则
;曲线
在点
处的切线方程为
.
已知函数
在
上单调递减,则
的取值范围是
.
已知函数
,若存在
,使得
,则
的取值范围是
.
三、解答题
已知函数
.
(1)
求函数
的单调区间;
(2)
求函数
在区间
上的值域.
已知函数
.
(1)
若曲线
在点
处的切线与
轴平行,且
,求
,
的值;
(2)
若
,
对任意
恒成立,求
的取值范围.
已知函数
.
(1)
若
,求
的极值;
(2)
证明:当
时,.
如图,已知
,
两个城镇相距
千米,设
是
的中点,在
的中垂线上有一高铁站
,,
的距离为
千米.为方便居民出行,在线段
上任取一点
(点
不与
,
重合)建设交通枢纽,从高铁站铺设快速路到
处,再铺设快速路分别到
,
两处.因地质条件等各种因素,其中快速路
造价为
百万元/千米,快速路
造价为
百万元/千米,快速路
造价为
百万元/千米.设
,总造价为
(单位:百万元).
(1)
求
关于
的函数关系式,并指出函数的定义域;
(2)
求总造价的最小值,并求出此时
的值.
已知函数
.
(1)
讨论函数
的单调性;
(2)
设函数
图象上不重合的两点
,().证明:(
是直线
的斜率).
已知函数
(
为自然对数的底数).
(1)
求函数
的零点
,以及曲线
在
处的切线方程;
(2)
设方程
有两个实数根
,,求证:
.
四、多选题
下列结论中正确的是
A.若
,则
B.若
,则
C.若
,则
D.若
,则
定义在区间
上的函数
的导函数
的图象如图所示,则下列结论正确的是
A.函数
在区间
上单调递增
B.函数
在区间
上单调递减
C.函数
在
处取得极大值
D.函数
在
处取得极小值
若实数
的取值使函数
在定义域上有两个极值点,则称函数
具有“凹凸趋向性”,已知
是函数
的导数,且
,当函数
具有“凹凸趋向性”时,
的取值范围的子集有
A.
B.
C.
D.
已知定义在
上的函数
的导函数为
,且
,,则下列判断正确的是
A.
B.
C.
D.
答案
一、选择题
1.
【答案】B
【解析】因为
,
所以
在区间
上的平均变化率为
.
故选B.
2.
【答案】B
【解析】对于A,,A错误;
对于B,,B正确;
对于C,,C错误;
对于D,,D错误.
故选B.
3.
【答案】B
【解析】由题得
,
所以
,
所以
,
解得
.
4.
【答案】C
【解析】由
,得
,
所以
,
所以
,
所以
,
所以
,
所以
.
5.
【答案】A
【解析】易知
为偶函数,
所以
,
因为
,当
时,,
所以
在
上为增函数,
所以
,
所以
.
故选A.
6.
【答案】A
【解析】因为
,
所以函数
是偶函数,
所以
的图象关于
轴对称,故排除B.
当
时,,故排除D.
当
时,,,当
时,
取最小值,且
,故排除C.
7.
【答案】B
【解析】设切点为
,由
,得
,
又直线
与曲线
相切,
所以
由②③得
,
代入①得
.
易得
,
代入①得
.
8.
【答案】D
【解析】由
,得
,令
,得
或
,当
时,,
所以
在
,
上单调递减,在
上单调递增,
又当
时,,所以
在
上为减函数,
又
,,所以
,,
由不等式
对任意的
恒成立,得
对任意的
恒成立,
所以
恒成立,
解得
,即
,
结合选项知,
的可能取值是
.
二、填空题
9.
【答案】
【解析】因为
,
所以
10.
【答案】
;
【解析】由
是定义在
上的奇函数知,,
所以
,
所以当
时,,
所以
,
又
,
所以
,
所以
,
所以
,,
所以
在
处的切线方程为
,
即
.
11.
【答案】
【解析】因为函数
在
上单调递减,
所以
在
上恒成立,即
在
上恒成立,
利用导数易知函数
在
上是增函数,
所以
,
故
.
12.
【答案】
【解析】因为
,
所以不妨设
.
当
时,.
当
时,,
根据
可知
,
所以
,,
所以
,
故
,
所以
,.
记
,则
,
于是易得
在
上单调递减,在
上单调递增,
所以
,
又当
时,,
所以
的值域是
.
所以
的取值范围是
.
三、解答题
13.
【答案】
(1)
由题意得,,
令
,得
,
令
,得
或
,
故函数
的单调递增区间为
,
单调递减区间为
,.
(2)
易知
,,,
因为
所以
.(或由
,,
可得
)
又当
时,,
所以函数
在区间
上的值域为
.
14.
【答案】
(1)
由
,得
,
由
得
(2)
因为
,
所以
,
对任意
恒成立等价于
对任意
恒成立,
令
,则
.
当
时,,
所以
在
上单调递减,
当
时,,
所以
在
上单调递增,
所以
,
所以
.
15.
【答案】
(1)
因为
,
所以
,
当
时,;
当
时,,
当
发生变化时,,
的变化情况如下表:因此,当
时,
有极大值,并且极大值为
,没有极小值.
(2)
令
,
则
,
由()知
在
上单调递增,在
上单调递减.
又
,,,
所以
在
上存在唯一零点,设为
,则
,
当
时,;当
时,,
所以
在区间
上单调递增,在区间
上单调递减,
又
,,
所以当
时,,
故
.
16.
【答案】
(1)
因为
,,
为
的中点,
所以
,,,
所以
(2)
设
则
令
,得
,
又
,
所以
.
当
时,,,
单调递减;
当
时,,,
单调递增.
所以
的最小值为
,此时总造价最小.
所以当
时,总造价最小,最小值为
百万元.
17.
【答案】
(1)
由题意得,函数
的定义域为
,且
①当
时,,
此时
在
上单调递增.
②当
时,令
,
得
或
(舍),,
由
得
,
由
得
,
所以
在
上单调递增,
在
上单调递减.
综上,当
时,函数
在
上单调递增;
当
时,函数
在
上单调递增,
在
上单调递减.
(2)
由题意得
,
,
所以
又
,
所以要证
成立,
只需证
成立,
即证
成立.
令
,
即证当
时,
成立.
设
,
则
,
所以函数
在
上是单调递增函数,
所以
,都有
,
即
,都有
,
所以
.
18.
【答案】
(1)
由
,得
,
所以函数
的零点
.
易得
,,,
所以曲线
在
处的切线方程为
.
,,
所以曲线
在
处的切线方程为
.
(2)
由()知
.
令
,得
.
当
时,;
当
时,.
所以
的单调递增区间为
,,
单调递减区间为
.
由()知,当
或
时,;
当
时,.
下面证明:当
时,.
当
时,
.
易知,
在
上单调递增,
所以
对任意
恒成立,
所以当
时,.
由
得
.
记
.
不妨设
,则
,
所以
.
要证
,只需证
,
即证
.
又因为
,
所以只需证
,
即
.
因为
,
所以
,
所以只需证
.
令
,则
.
当
时,,
为单调递减函数;
当
时,,
为单调递增函数.
所以
,
所以
,
所以
.
四、多选题
19.
【答案】A;B;C
【解析】选项A中,若
,则
,故A正确;
选项B中,若
,则
,令
,则
,解得
,故B正确;
选项C中,若
,则
,故C正确;
选项D中,若
,则
,故D错误.
故选ABC.
20.
【答案】A;B;D
【解析】由
的图象知,当
时,;
当
时,,
因此
在
上单调递减,在
上单调递增,故A,B正确.
在
附近单调递增,在
处不取极大值,故C错误.
由
在
上单调递减,在
上单调递增,得
在
处取得极小值,故D正确.
21.
【答案】B;D
【解析】依题意得
,
若函数
具有“凹凸趋向性”,则
在
上有
个不同的实数根,
令
,则
,
令
,解得
,令
,解得
,
所以
在
上单调递减,在
上单调递增,
故
的最小值是
,当
时,,故
.
22.
【答案】C;D
【解析】令
,,
则
,
因为
,
所以
在
上恒成立,
因此函数
在
上单调递减,
因此
,
即
,
即
,
故A错误;
又
,
所以
,
所以
在
上恒成立,
因为
,
所以
,
故B错误;
又
,
所以
,
即
,
故C正确;
又
,
所以
,
即
,
故D正确.
