6.1分类加法计数原理与分步乘法计数原理-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册讲义(word含答案)
文档属性
| 名称 | 6.1分类加法计数原理与分步乘法计数原理-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册讲义(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 373.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 18:24:47 | ||
图片预览



文档简介
1087120-198755第六章计数原理
第六章计数原理
762000156845 6.1分类加法计数原理与分步乘法计数原理
6.1分类加法计数原理与分步乘法计数原理
134620175260 知识点1-----分类加法计数原理
知识点1-----分类加法计数原理
任务
分类
完成一件事
有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法
完成这件事共有N种='m+n种不同的方法
计数
任务
分类
完成一件事
有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法
完成这件事共有N种='m+n种不同的方法
计数
233362522860基本原理 N=m+n
原理推广 N=false+false...+false
基本原理 N=m+n
原理推广 N=false+false...+false
知识点2-----分步乘法计数原理
任务
分类
完成一件事
需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法
完成这件事共有N种='m×n种不同的方法
计数
任务
分类
完成一件事
需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法
完成这件事共有N种='m×n种不同的方法
计数
2364740-96520基本原理 N=m×n,
原理推广 N=false·false...·false
基本原理 N=m×n,
原理推广 N=false·false...·false
-6350062230 知识点3------分类加法计数原理与分步乘法计数原理的联系与区别
知识点3------分类加法计数原理与分步乘法计数原理的联系与区别
(1)联系:都是涉及做一件事的不同方法的种数问题.
(2)区别:分类加法计数原理针对的是“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事;分步乘法计数原理针对的是“分步”问题,各个步骤中的方
法互相依存,只有各个步骤都完成才算做完这件事.
-88265117475 知识点4-----使用分类加法计数原理计数的两个条件
知识点4-----使用分类加法计数原理计数的两个条件
(1)根据问题的特点能确定一个适合于它的分类标准,然后在这个标准下进行分类.
(2)完成这件事的任何一种方法必须属于某一类,并且分别属于不同类的两种方法是不同的方法,只有满足这些条件,才可以用分类加法计数原理.
2.利用分类加法计数原理计数时的解题流程
-102870395605 知识点5-----使用分步乘法计数原理计数的两个注意点
知识点5-----使用分步乘法计数原理计数的两个注意点
一是:要按照事件发生的过程合理分步,即分步是有先后顺序的;
二是:各步中的方法互相依存,缺一不可,只有各个步骤都完成才算完成这件事.
2.利用分步乘法计数原理计数时的解题流程
利用两个计数原理解题时的三个注意点
(1)当题目无从下手时,可考虑要完成的这件事是什么,即怎样做才算完成这件事,然后给出完成这件事的一种或几种方法,从这几种方法中归纳出解题方法.
(2)分类时标准要明确,做到不重不漏,有时要恰当画出示意图或树形图,使问题的分析更直观、清楚,便于探索规律.
(3)混合问题一般是先分类再分步.
-40005121285【防范措施】明确“分类”与“分步”
“分类”是其中任何一类中的任何一种方法均可独立完成所给事情,而“分步”必须是把各个步骤均完成才能完成所给事情.在解题过程中要能高效地得到正确结论必须将要计的数准确进行“分类”或是“分步”,如本例是“分步”,而非“分类”问题.
【防范措施】明确“分类”与“分步”
“分类”是其中任何一类中的任何一种方法均可独立完成所给事情,而“分步”必须是把各个步骤均完成才能完成所给事情.在解题过程中要能高效地得到正确结论必须将要计的数准确进行“分类”或是“分步”,如本例是“分步”,而非“分类”问题.
7175564770 要点探究
要点探究
分类加法计数原理
对分类加法计数原理的三点说明
核心:原理的核心是“分类”,完成一件事要分为若干类,各类的方法相互独立,各类中的各种方法也相互独立,并且用任何一类中任何一种方法都可以单独完成这件事,因此在应用原理时一定要根据问题的特点确定一个分类的标准,然后在确定的标准下进行分类,其次还要注意分类不能重复,不能遗漏.
(2)目的:原理的目的是求解“完成一件事的不同方法数”,因此在应用原理解题时要有问题意识,明确并努力思考两个问题,即问题要求我们完成一件什么事,如何完成这件事.
(3)推广:原理可以推广到n类不同的方案
分步乘法计数原理
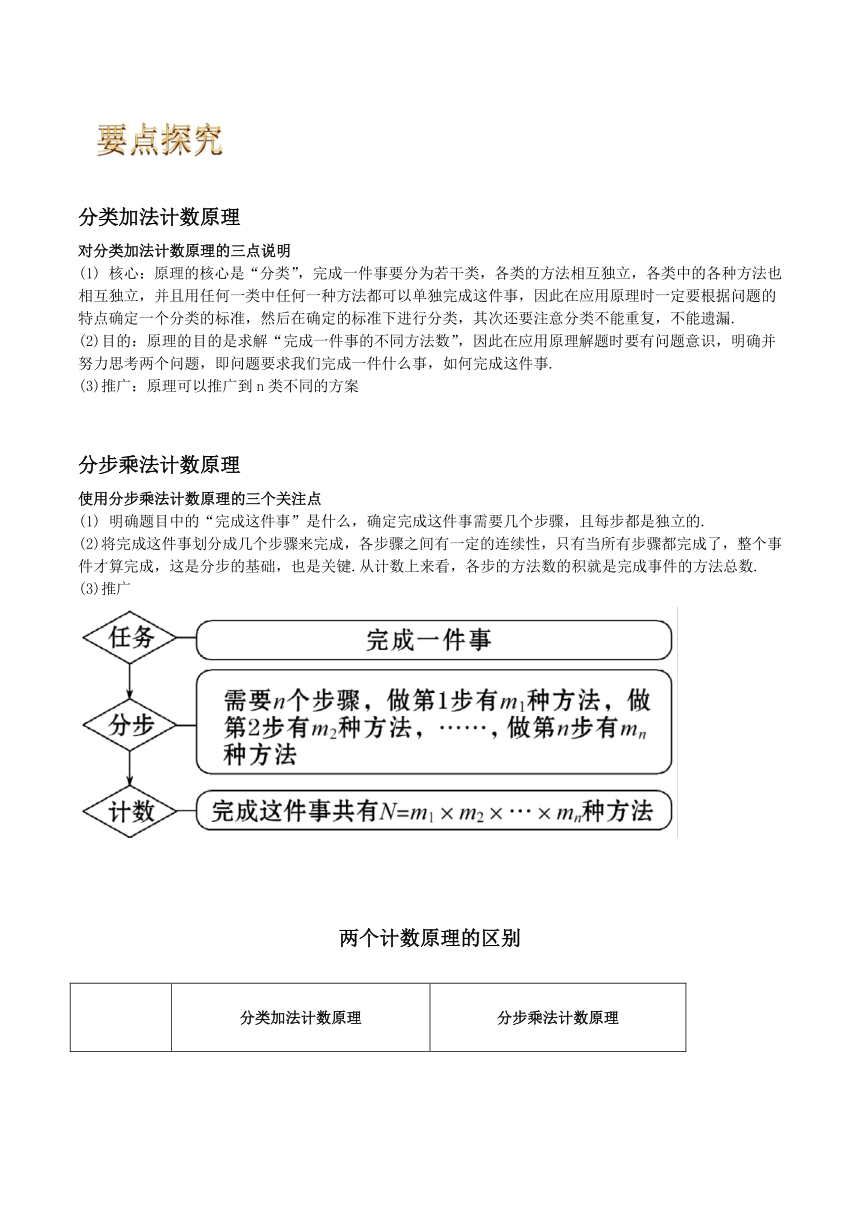
使用分步乘法计数原理的三个关注点
明确题目中的“完成这件事”是什么,确定完成这件事需要几个步骤,且每步都是独立的.
(2)将完成这件事划分成几个步骤来完成,各步骤之间有一定的连续性,只有当所有步骤都完成了,整个事件才算完成,这是分步的基础,也是关键.从计数上来看,各步的方法数的积就是完成事件的方法总数.
(3)推广
两个计数原理的区别
分类加法计数原理
分步乘法计数原理
区别一
每类办法都能独立完成这件事.它是独立的、一次的且每次得到的是最后结果,只需一种方法就完成
任何一步都不能独立完成这件事,缺少任何一步也不可,只有各步骤都完成了才能完成这件事
区别二
各类办法之间是互斥的,并列的,独立的
各步之间是相互依存的,并且既不能重复,也不能遗漏
212090-62865经典例题
经典例题
例题1.某班有男生28名、女生20名,从该班选出学生代表参加校学代会.
(1)若学校分配给该班1名代表,则有多少种不同的选法?
(2)若学校分配给该班2名代表,且男、女生代表各1名,则有多少种不同的选法?
【答案】 (1)解:选出1名代表,可以选男生,也可以选女生,因此完成“选1名代表”这件事分2类:
第1类,从男生中选出1名代表,有28种不同方法;
第2类,从女生中选出1名代表,有20种不同方法.
根据分类加法计数原理,共有28+20=48种不同的选法.
(2)解:完成“选出男、女生代表各1名”这件事,可以分2步完成:
第1步,选1名男生代表,有28种不同方法;
第2步,选1名女生代表,有20种不同方法.
根据分步乘法计数原理,共有28×20=560种不同的选法.
【解析】(1)根据分类计数原理,分别求出选择男生和女生的不同方法,最后求和即可;(2)根据分步计数原理,分别求出选择男生和女生的不同方法,最后求积即可;
例题2.用n种不同的颜色为下列两块广告牌着色,(如图甲、乙),要求在A,B,C,D四个区域中相邻(有公共边界)的区域不用同一颜色.
?
(1)若n=6,则为甲图着色时共有多少种不同的方法;
(2)若为乙图着色时共有120种不同方法,求n.
【答案】 (1)解:对区域A,B,C,D按顺序着色,
共有6×5×4×4=480(种)
(2)解:对区域A,B,C,D按顺序着色,依次有n种、n-1种、n-2种和n-3种,由分步乘法计数原理,不同的着色方法共有n(n-1)(n-2(n-3)=120,整理得(n2-3n)(n2-3n+2)=120,(n2-3n)2+2(n2-3n)-120=0
n2-3n-10=0或n2-3n+12=0(舍去),解得n=5
【解析】(1)根据分步计数原理进行计算即可;
(2) 对区域A,B,C,D按顺序着色 , 由分步乘法计数原理 ,列出方程求解即可。
例题3. 5名男生3名女生参加升旗仪式:
(1)站两横排,3名女生站前排,5名男生站后排有多少种站法?
(2)站两纵列,每列4人,每列都有女生且女生站在男生前面,有多少种排列方法?
【答案】 (1)解:分两步求解:
①先排前排的3名女生,有 A33=6 种不同的方法;
②再排后排的5名男生,有 A55=120 种不同的方法.
由分步乘法计数原理可得共有 A33A55=6×120=720 种不同的站法.
(2)解:将3名女生分为两组,有 C31 种方法,然后选择其中的一列将1名女生排在最前的一个位置上,有 C21 种方法,然后再从5名男生中选取3名排在该女生的后边,有 A53 种方法;然后再排另外一列,将剩余的2名女生排再该列的前边有 A22 种方法,再将剩余的2名男生排在这2名女生的后边,有 A22 种方法.
由分步乘法计数原理可得不同的排列方法有 C31C21A53A22A22=1440 种.
【解析】(1)利用实际问题的已知条件结合分步乘法计数原理,得出3名女生站前排,5名男生站后排的站法种数。
(2)利用实际问题的已知条件结合分步乘法计数原理,得出站两纵列,每列4人,每列都有女生且女生站在男生前面的排列方法种数。
例题4.四个不同的小球放入编号为1,2,3,4的四个盒子中.
(1)若每个盒子放一个球,则共有多少种不同的放法?
(2)恰有一个空盒的放法共有多少种?
【答案】(1)解:每个盒子放一个球,共有 A44 =24种不同的放法
(2)解:先选后排,分三步完成:
第一步:四个盒子中选一只为空盒,有4种选法;
第二步:选两球为一个元素,有 C42=6 种选法;
第三步:三个元素放入三个盒中,有 A33=6 种放法.
故共有4×6×6=144种放法
【解析】(1)每个小球都有4种放法,利用排列公式即可;
(2)先选两个元素作为一组再排列,恰有一个盒子有2个小球,从4个小球中选2个作为一个元素,与另外两个元素一球在三个位置全排列,根据分布计数原理即可.
95250373380随堂练习
随堂练习
练习1. 6男4女站成一排,求满足下列条件的排法各有多少种?(用式子表达)
(1)男甲必排在首位;
(2)男甲、男乙必排在正中间;
(3)男甲不在首位,男乙不在末位;
(4)男甲、男乙必排在一起;
(5)4名女生排在一起;
(6)任何两个女生都不得相邻;
(7)男生甲、乙、丙顺序一定.
练习2.在一次合唱中有6个女生(其中有1个领唱)和2个男生分成两排表演.
(1)每排4人,问共有多少种不同的排法?
(2)领唱站在前排,男生站在后排,还是每排4人,问有多少种不同的排法?
练习3.由数字1,2,3,4,5组成无重复数字的五位数.
(1)共可以组成多少个五位数?
(2)其中奇数有多少个?
(3)如果将所有的五位数按从小到大的顺序排列,43125是第几个数?说明理由.
练习4.排列组合
(1)7位同学站成一排,甲、乙两同学必须相邻的排法共有多少种?
(2)7位同学站成一排,甲、乙和丙三个同学都不能相邻的排法共有多少种?
(3)7位同学站成一排,甲不站排头,乙不站排尾,不同站法种数有多少种?
142240-100965参考答案
参考答案
练习1【答案】 解:(1)男甲必排在首位,则其他人任意排,故有A99种,
(2)男甲、男乙必排在正中间,则其他人任意排,故有A22A77种,
(3)男甲不在首位,男乙不在末位,利用间接法,故有A1010﹣2A99+A88种,
(4)男甲、男乙必排在一起,利用捆绑法,把甲乙两人捆绑在一起看作一个复合元素和另外全排,故有A22A88种,
(5)4名女生排在一起,利用捆绑法,把4名女生捆绑在一起看作一个复合元素和另外全排,故有A44A77种,
(6)任何两个女生都不得相邻,利用插空法,故有A66A74种,
(7)男生甲、乙、丙顺序一定,利用定序法,A1010A33=A107种
【解析】(1)男甲必排在首位,则其他人任意排,问题得以解决.
(2)男甲、男乙必排在正中间,则其他人任意排,问题得以解决,
(3)男甲不在首位,男乙不在末位,利用间接法,故问题得以解决,
(4)男甲、男乙必排在一起,利用捆绑法,问题得以解决,
(5)4名女生排在一起,利用捆绑法,问题得以解决,
(6)任何两个女生都不得相邻,利用插空法,问题得以解决,
(7)男生甲、乙、丙顺序一定,利用定序法,问题得以解决.
练习2【答案】 解:(1)每排4人,和排成一排的站法一样,故有A88=40320种,
(2)从另外的5个女生选3个和领唱全排,其余的4人也全排,根据分步计数原理可得,C53A44A44=5760=5 760种不同的排法.
【解析】(1)由题意可知每排4人,和排成一排的站法一样,故把8人全排即可,
)从另外的5个女生选3个和领唱全排,其余的4人也全排,根据分步计数原理可得.
练习3【答案】 (1)解:由数字1,2,3,4,5组成无重复数字的五位数,共可以组成A55=120个五位数
(2)解:∵由1、2、3、4、5组成的无重复数字的五位数中奇数,
∴第五个数字必须从1、3、5中选出,共有C31种结果,
其余四个位置可以用四个元素在四个位置进行全排列,共有A44种结果,
根据分步计数原理得到共有C31A44=72
(3)解:根据题意,用1、2、3、4、5这五个数字组成无重复数字的五位数,有A55=120种情况,即一共有120个五位数,
再考虑大于43125的数,分为以下四类讨论:
①5在首位,将其他4个数字全排列即可,有A44=24个,
②4在首位,5在千位,将其他3个数字全排列即可,有A33=6个,
③4在首位,3在千位,5在百位,将其他2个数字全排列即可,有A22=2个,
④43215,43251,43152,共3个
故不大于43251的五位数有120﹣(24+6+2﹣3)=85个,
即43125是第85项.
【解析】(1)利用全排列,可得结论;(2)由1、2、3、4、5组成的无重复数字的五位数中奇数,第五位是有限制条件的元素,第五个数字必须从1、3、5中选出,其余四个位置可以用四个元素在四个位置进行全排列;(3)根据题意,先有排列数公式求出用1、2、3、4、5这五个数字组成无重复数字的五位数的个数,再分4种情况讨论分析大于43125的数个数,由间接法分析可得答案.
练习4【答案】 (1)解:先将甲、乙两位同学“捆绑”在一起看成一个元素与其余的5个元素(同学)一起进行全排列有A66种方法;
再将甲、乙两个同学“松绑”进行排列有A22种方法.所以这样的排法一共有A66A22=1440种
(2)解:将甲、乙和丙三个同学插入到除甲、乙和丙之外4人全排所形成的5个空中的3个,故有A44A53=1440种
(3)解:甲站排头,或乙站排尾有2A66﹣A55种不同的排法,
∴甲不站排头,且乙不站排尾有: A77-2A66+A55=3720 种不同的排法
【解析】对这几个事件不同排法和数的计算,根据分步原理与分类原理直接计算即可.
第六章计数原理
762000156845 6.1分类加法计数原理与分步乘法计数原理
6.1分类加法计数原理与分步乘法计数原理
134620175260 知识点1-----分类加法计数原理
知识点1-----分类加法计数原理
任务
分类
完成一件事
有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法
完成这件事共有N种='m+n种不同的方法
计数
任务
分类
完成一件事
有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法
完成这件事共有N种='m+n种不同的方法
计数
233362522860基本原理 N=m+n
原理推广 N=false+false...+false
基本原理 N=m+n
原理推广 N=false+false...+false
知识点2-----分步乘法计数原理
任务
分类
完成一件事
需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法
完成这件事共有N种='m×n种不同的方法
计数
任务
分类
完成一件事
需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法
完成这件事共有N种='m×n种不同的方法
计数
2364740-96520基本原理 N=m×n,
原理推广 N=false·false...·false
基本原理 N=m×n,
原理推广 N=false·false...·false
-6350062230 知识点3------分类加法计数原理与分步乘法计数原理的联系与区别
知识点3------分类加法计数原理与分步乘法计数原理的联系与区别
(1)联系:都是涉及做一件事的不同方法的种数问题.
(2)区别:分类加法计数原理针对的是“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事;分步乘法计数原理针对的是“分步”问题,各个步骤中的方
法互相依存,只有各个步骤都完成才算做完这件事.
-88265117475 知识点4-----使用分类加法计数原理计数的两个条件
知识点4-----使用分类加法计数原理计数的两个条件
(1)根据问题的特点能确定一个适合于它的分类标准,然后在这个标准下进行分类.
(2)完成这件事的任何一种方法必须属于某一类,并且分别属于不同类的两种方法是不同的方法,只有满足这些条件,才可以用分类加法计数原理.
2.利用分类加法计数原理计数时的解题流程
-102870395605 知识点5-----使用分步乘法计数原理计数的两个注意点
知识点5-----使用分步乘法计数原理计数的两个注意点
一是:要按照事件发生的过程合理分步,即分步是有先后顺序的;
二是:各步中的方法互相依存,缺一不可,只有各个步骤都完成才算完成这件事.
2.利用分步乘法计数原理计数时的解题流程
利用两个计数原理解题时的三个注意点
(1)当题目无从下手时,可考虑要完成的这件事是什么,即怎样做才算完成这件事,然后给出完成这件事的一种或几种方法,从这几种方法中归纳出解题方法.
(2)分类时标准要明确,做到不重不漏,有时要恰当画出示意图或树形图,使问题的分析更直观、清楚,便于探索规律.
(3)混合问题一般是先分类再分步.
-40005121285【防范措施】明确“分类”与“分步”
“分类”是其中任何一类中的任何一种方法均可独立完成所给事情,而“分步”必须是把各个步骤均完成才能完成所给事情.在解题过程中要能高效地得到正确结论必须将要计的数准确进行“分类”或是“分步”,如本例是“分步”,而非“分类”问题.
【防范措施】明确“分类”与“分步”
“分类”是其中任何一类中的任何一种方法均可独立完成所给事情,而“分步”必须是把各个步骤均完成才能完成所给事情.在解题过程中要能高效地得到正确结论必须将要计的数准确进行“分类”或是“分步”,如本例是“分步”,而非“分类”问题.
7175564770 要点探究
要点探究
分类加法计数原理
对分类加法计数原理的三点说明
核心:原理的核心是“分类”,完成一件事要分为若干类,各类的方法相互独立,各类中的各种方法也相互独立,并且用任何一类中任何一种方法都可以单独完成这件事,因此在应用原理时一定要根据问题的特点确定一个分类的标准,然后在确定的标准下进行分类,其次还要注意分类不能重复,不能遗漏.
(2)目的:原理的目的是求解“完成一件事的不同方法数”,因此在应用原理解题时要有问题意识,明确并努力思考两个问题,即问题要求我们完成一件什么事,如何完成这件事.
(3)推广:原理可以推广到n类不同的方案
分步乘法计数原理
使用分步乘法计数原理的三个关注点
明确题目中的“完成这件事”是什么,确定完成这件事需要几个步骤,且每步都是独立的.
(2)将完成这件事划分成几个步骤来完成,各步骤之间有一定的连续性,只有当所有步骤都完成了,整个事件才算完成,这是分步的基础,也是关键.从计数上来看,各步的方法数的积就是完成事件的方法总数.
(3)推广
两个计数原理的区别
分类加法计数原理
分步乘法计数原理
区别一
每类办法都能独立完成这件事.它是独立的、一次的且每次得到的是最后结果,只需一种方法就完成
任何一步都不能独立完成这件事,缺少任何一步也不可,只有各步骤都完成了才能完成这件事
区别二
各类办法之间是互斥的,并列的,独立的
各步之间是相互依存的,并且既不能重复,也不能遗漏
212090-62865经典例题
经典例题
例题1.某班有男生28名、女生20名,从该班选出学生代表参加校学代会.
(1)若学校分配给该班1名代表,则有多少种不同的选法?
(2)若学校分配给该班2名代表,且男、女生代表各1名,则有多少种不同的选法?
【答案】 (1)解:选出1名代表,可以选男生,也可以选女生,因此完成“选1名代表”这件事分2类:
第1类,从男生中选出1名代表,有28种不同方法;
第2类,从女生中选出1名代表,有20种不同方法.
根据分类加法计数原理,共有28+20=48种不同的选法.
(2)解:完成“选出男、女生代表各1名”这件事,可以分2步完成:
第1步,选1名男生代表,有28种不同方法;
第2步,选1名女生代表,有20种不同方法.
根据分步乘法计数原理,共有28×20=560种不同的选法.
【解析】(1)根据分类计数原理,分别求出选择男生和女生的不同方法,最后求和即可;(2)根据分步计数原理,分别求出选择男生和女生的不同方法,最后求积即可;
例题2.用n种不同的颜色为下列两块广告牌着色,(如图甲、乙),要求在A,B,C,D四个区域中相邻(有公共边界)的区域不用同一颜色.
?
(1)若n=6,则为甲图着色时共有多少种不同的方法;
(2)若为乙图着色时共有120种不同方法,求n.
【答案】 (1)解:对区域A,B,C,D按顺序着色,
共有6×5×4×4=480(种)
(2)解:对区域A,B,C,D按顺序着色,依次有n种、n-1种、n-2种和n-3种,由分步乘法计数原理,不同的着色方法共有n(n-1)(n-2(n-3)=120,整理得(n2-3n)(n2-3n+2)=120,(n2-3n)2+2(n2-3n)-120=0
n2-3n-10=0或n2-3n+12=0(舍去),解得n=5
【解析】(1)根据分步计数原理进行计算即可;
(2) 对区域A,B,C,D按顺序着色 , 由分步乘法计数原理 ,列出方程求解即可。
例题3. 5名男生3名女生参加升旗仪式:
(1)站两横排,3名女生站前排,5名男生站后排有多少种站法?
(2)站两纵列,每列4人,每列都有女生且女生站在男生前面,有多少种排列方法?
【答案】 (1)解:分两步求解:
①先排前排的3名女生,有 A33=6 种不同的方法;
②再排后排的5名男生,有 A55=120 种不同的方法.
由分步乘法计数原理可得共有 A33A55=6×120=720 种不同的站法.
(2)解:将3名女生分为两组,有 C31 种方法,然后选择其中的一列将1名女生排在最前的一个位置上,有 C21 种方法,然后再从5名男生中选取3名排在该女生的后边,有 A53 种方法;然后再排另外一列,将剩余的2名女生排再该列的前边有 A22 种方法,再将剩余的2名男生排在这2名女生的后边,有 A22 种方法.
由分步乘法计数原理可得不同的排列方法有 C31C21A53A22A22=1440 种.
【解析】(1)利用实际问题的已知条件结合分步乘法计数原理,得出3名女生站前排,5名男生站后排的站法种数。
(2)利用实际问题的已知条件结合分步乘法计数原理,得出站两纵列,每列4人,每列都有女生且女生站在男生前面的排列方法种数。
例题4.四个不同的小球放入编号为1,2,3,4的四个盒子中.
(1)若每个盒子放一个球,则共有多少种不同的放法?
(2)恰有一个空盒的放法共有多少种?
【答案】(1)解:每个盒子放一个球,共有 A44 =24种不同的放法
(2)解:先选后排,分三步完成:
第一步:四个盒子中选一只为空盒,有4种选法;
第二步:选两球为一个元素,有 C42=6 种选法;
第三步:三个元素放入三个盒中,有 A33=6 种放法.
故共有4×6×6=144种放法
【解析】(1)每个小球都有4种放法,利用排列公式即可;
(2)先选两个元素作为一组再排列,恰有一个盒子有2个小球,从4个小球中选2个作为一个元素,与另外两个元素一球在三个位置全排列,根据分布计数原理即可.
95250373380随堂练习
随堂练习
练习1. 6男4女站成一排,求满足下列条件的排法各有多少种?(用式子表达)
(1)男甲必排在首位;
(2)男甲、男乙必排在正中间;
(3)男甲不在首位,男乙不在末位;
(4)男甲、男乙必排在一起;
(5)4名女生排在一起;
(6)任何两个女生都不得相邻;
(7)男生甲、乙、丙顺序一定.
练习2.在一次合唱中有6个女生(其中有1个领唱)和2个男生分成两排表演.
(1)每排4人,问共有多少种不同的排法?
(2)领唱站在前排,男生站在后排,还是每排4人,问有多少种不同的排法?
练习3.由数字1,2,3,4,5组成无重复数字的五位数.
(1)共可以组成多少个五位数?
(2)其中奇数有多少个?
(3)如果将所有的五位数按从小到大的顺序排列,43125是第几个数?说明理由.
练习4.排列组合
(1)7位同学站成一排,甲、乙两同学必须相邻的排法共有多少种?
(2)7位同学站成一排,甲、乙和丙三个同学都不能相邻的排法共有多少种?
(3)7位同学站成一排,甲不站排头,乙不站排尾,不同站法种数有多少种?
142240-100965参考答案
参考答案
练习1【答案】 解:(1)男甲必排在首位,则其他人任意排,故有A99种,
(2)男甲、男乙必排在正中间,则其他人任意排,故有A22A77种,
(3)男甲不在首位,男乙不在末位,利用间接法,故有A1010﹣2A99+A88种,
(4)男甲、男乙必排在一起,利用捆绑法,把甲乙两人捆绑在一起看作一个复合元素和另外全排,故有A22A88种,
(5)4名女生排在一起,利用捆绑法,把4名女生捆绑在一起看作一个复合元素和另外全排,故有A44A77种,
(6)任何两个女生都不得相邻,利用插空法,故有A66A74种,
(7)男生甲、乙、丙顺序一定,利用定序法,A1010A33=A107种
【解析】(1)男甲必排在首位,则其他人任意排,问题得以解决.
(2)男甲、男乙必排在正中间,则其他人任意排,问题得以解决,
(3)男甲不在首位,男乙不在末位,利用间接法,故问题得以解决,
(4)男甲、男乙必排在一起,利用捆绑法,问题得以解决,
(5)4名女生排在一起,利用捆绑法,问题得以解决,
(6)任何两个女生都不得相邻,利用插空法,问题得以解决,
(7)男生甲、乙、丙顺序一定,利用定序法,问题得以解决.
练习2【答案】 解:(1)每排4人,和排成一排的站法一样,故有A88=40320种,
(2)从另外的5个女生选3个和领唱全排,其余的4人也全排,根据分步计数原理可得,C53A44A44=5760=5 760种不同的排法.
【解析】(1)由题意可知每排4人,和排成一排的站法一样,故把8人全排即可,
)从另外的5个女生选3个和领唱全排,其余的4人也全排,根据分步计数原理可得.
练习3【答案】 (1)解:由数字1,2,3,4,5组成无重复数字的五位数,共可以组成A55=120个五位数
(2)解:∵由1、2、3、4、5组成的无重复数字的五位数中奇数,
∴第五个数字必须从1、3、5中选出,共有C31种结果,
其余四个位置可以用四个元素在四个位置进行全排列,共有A44种结果,
根据分步计数原理得到共有C31A44=72
(3)解:根据题意,用1、2、3、4、5这五个数字组成无重复数字的五位数,有A55=120种情况,即一共有120个五位数,
再考虑大于43125的数,分为以下四类讨论:
①5在首位,将其他4个数字全排列即可,有A44=24个,
②4在首位,5在千位,将其他3个数字全排列即可,有A33=6个,
③4在首位,3在千位,5在百位,将其他2个数字全排列即可,有A22=2个,
④43215,43251,43152,共3个
故不大于43251的五位数有120﹣(24+6+2﹣3)=85个,
即43125是第85项.
【解析】(1)利用全排列,可得结论;(2)由1、2、3、4、5组成的无重复数字的五位数中奇数,第五位是有限制条件的元素,第五个数字必须从1、3、5中选出,其余四个位置可以用四个元素在四个位置进行全排列;(3)根据题意,先有排列数公式求出用1、2、3、4、5这五个数字组成无重复数字的五位数的个数,再分4种情况讨论分析大于43125的数个数,由间接法分析可得答案.
练习4【答案】 (1)解:先将甲、乙两位同学“捆绑”在一起看成一个元素与其余的5个元素(同学)一起进行全排列有A66种方法;
再将甲、乙两个同学“松绑”进行排列有A22种方法.所以这样的排法一共有A66A22=1440种
(2)解:将甲、乙和丙三个同学插入到除甲、乙和丙之外4人全排所形成的5个空中的3个,故有A44A53=1440种
(3)解:甲站排头,或乙站排尾有2A66﹣A55种不同的排法,
∴甲不站排头,且乙不站排尾有: A77-2A66+A55=3720 种不同的排法
【解析】对这几个事件不同排法和数的计算,根据分步原理与分类原理直接计算即可.
