3.5 确定圆的条件 一课一练(含解析)
文档属性
| 名称 | 3.5 确定圆的条件 一课一练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 08:58:34 | ||
图片预览



文档简介
初中数学北师大版九年级下学期 第三章 3.5 确定圆的条件
一、单选题
1.给定下列条件可以确定一个圆的是(?? )
A.?已知圆心??????????????????????B.?已知半径??????????????????????C.?已知直径??????????????????????D.?不在同一直线上三点
2.若三角形的外心在这个三角形的一边上,则这个三角形是(??? ).
A.?锐角三角形????????????????????????B.?直角三角形????????????????????????C.?钝角三角形????????????????????????D.?不能确定
3.三角形的外心具有的性质是( ???)
A.?到三边距离相等???????????B.?到三个顶点距离相等???????????C.?外心在三角形外???????????D.?外心在三角形内
4.下列条件中,能确定圆的是(? ?)
A.?以已知点O为圆心???????????????????????????????????????????????B.?以1cm长为半径
C.?经过已知点A,且半径为2cm??????????????????????????????D.?以点O为圆心,1cm为半径
5.如图为4×4的正方形网格,A,B,C,D,O均在格点上,点O是(?? )
A.?△ACD的外心????????????????????B.?△ABC的外心????????????????????C.?△ACD的内心????????????????????D.?△ABC的内心
6.如图,点O是△ABC的内切圆的圆心,若∠A=80°,则∠BOC为(? )
A.?100°?????????????????????????????????????B.?130°?????????????????????????????????????C.?50°?????????????????????????????????????D.?65°
7.已知:不在同一直线上的三点A,B,C
求作:⊙O,使它经过点A,B,C
作法:如图,
⑴连接AB ,作线段AB的垂直平分线DE;
⑵连接BC ,作线段BC的垂直平分线FG,交DE于点O;
⑶以O为圆心,OB 长为半径作⊙O.
⊙O就是所求作的圆.
根据以上作图过程及所作图形,下列结论中正确的是(?? )
A.?连接AC, 则点O是△ABC的内心????????????????????????????B.?
C.?连接OA,OC,则OA, OC不是⊙O的半径?????????????D.?若连接AC, 则点O在线段AC的垂直平分线上
8.现有如下4个命题:
①过两点可以作无数个圆.②三点可以确定一个圆.③任意一个三角形有且只有一个外接圆.④任意一个圆有且只有一个内接三角形.其中正确的有 ??
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
9.中,两条直角边的长分别是6cm和8cm,则 的外接圆的半径是________cm.
10.已知O为△ABC的外接圆圆心,若O在△ABC外,则△ABC是________(填“锐角三角形”或“直角三角形”或“钝角三角形”).
11.如图,在平面直角坐标系 中,点 的坐标分别是 是 的外接圆,则圆心 的坐标为________, 的半径为________.
12.已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.如果∠ACB=75°,圆O的半径为2,则BD的长为________.
13.已知△ABC的三边a,b,c,满足a+b2+|c﹣6|+28=4 +10b,则△ABC的外接圆半径=________.
三、解答题
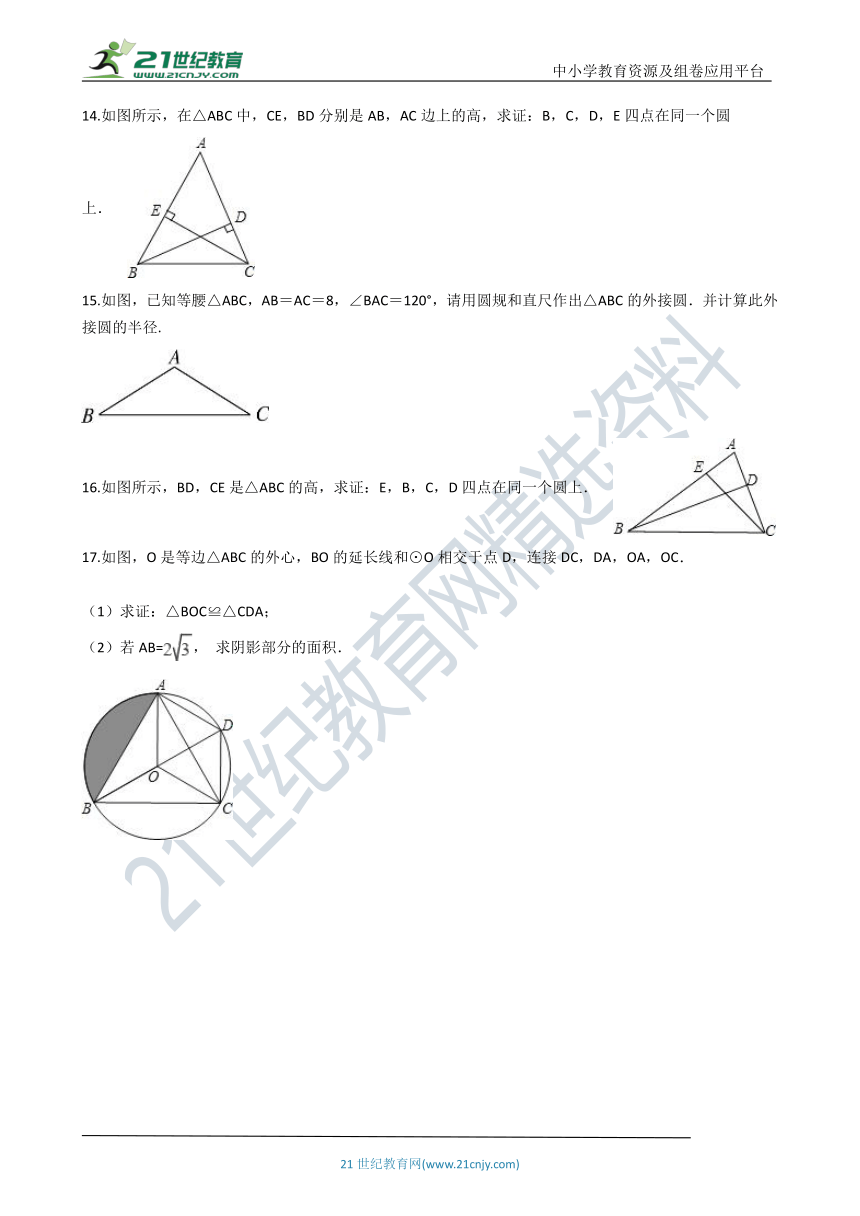
14.如图所示,在△ABC中,CE,BD分别是AB,AC边上的高,求证:B,C,D,E四点在同一个圆上.
15.如图,已知等腰△ABC,AB=AC=8,∠BAC=120°,请用圆规和直尺作出△ABC的外接圆.并计算此外接圆的半径.
16.如图所示,BD,CE是△ABC的高,求证:E,B,C,D四点在同一个圆上.
17.如图,O是等边△ABC的外心,BO的延长线和⊙O相交于点D,连接DC,DA,OA,OC.
(1)求证:△BOC≌△CDA;
(2)若AB=, 求阴影部分的面积.
答案解析部分
一、单选题
1.【答案】 D
解:A、不能确定.因为半径不确定,故不符合题意;
B、不能确定.因为圆心的位置不确定,故不符合题意;
C、不能确定,因为圆心的位置不确定,故不符合题意;
D.不在同一直线上三点可以确定一个圆.故符合题意;
故答案为:D.
2.【答案】 B
解:∵根据圆周角定理:直径所对的圆周角是直角,
∴该三角形是直角三角形.
故答案为:B.
3.【答案】 B
解:三角形的外心是三角形三条垂直平分线的交点
∴外心到三角形的顶点的距离相等。
故答案为:B.
4.【答案】 D
解:∵圆心确定,半径确定后就可以确定圆,
∴D选项符合题意,
故答案为:D.
5.【答案】 B
解:由图可得:OA=OB=OC= ,
所以点O在△ABC的外心上,
故答案为:B.
6.【答案】 B
解:∵点O是△ABC的内切圆的圆心,∴∠OBC= ∠ABC,∠OCB= ∠ACB.
∵∠A=80°,∴∠ABC+∠ACB=180°﹣∠A=100°,∴∠OBC+∠OCB= (∠ABC+∠ACB)=50°,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣50°=130°.
故答案为:B.
7.【答案】 D
解:A:连接AC, 根据题意可知,点O是△ABC的外心,故 A不符合题意;
B: 根据题意无法证明 ,故 B不符合题意;
C: 连接OA,OC,则OA, OC是⊙O的半径,故 C不符合题意
D: 若连接AC, 则点O在线段AC的垂直平分线上,故 D符合题意
故答案为:D.
8.【答案】 B
解:①过两点可以作无数个圆,是真命题.
②不在同一直线上的三点可以确定一个圆,是假命题.
③任意一个三角形有且只有一个外接圆,是真命题.
④任意一个圆有无数个一个内接三角形,是假命题;
故选:
二、填空题
9.【答案】 5
解:由勾股定理得: 的斜边长为 ,
直角三角形的外接圆的圆心为斜边的中点,
的外接圆的半径为 ,
故答案为:5.
10.【答案】 钝角三角形
解:∵锐角三角形的外心在三角形的内部;直角三角形的外心为直角三角形斜边的中点;钝角三角形的外心在三角形的外部.
又∵O为△ABC的外接圆圆心,若O在△ABC外,
∴△ABC是钝角三角形,
故答案为:钝角三角形.
11.【答案】 (3,3);
解:∵点A,B,C的坐标分别是(0,2),(2,0),(4,0),
∴BC的垂直平分线为直线x=3,
∵OA=OB,
∴△OAB为等腰直角三角形,
∴AB的垂直平分线为第一、三象限的角平分线,即直线y=x,
∵直线x=3与直线y=x的交点为M点,
∴M点的坐标为(3,3),
∵ ,
∴⊙M的半径为 .
故答案为(3,3), .
12.【答案】 2
解:如图,
连接OB,
∵∠DOC=2∠ACD=90°.
∴∠ACD=45°,
∵∠ACB=75°,
∴∠BCD=∠ACB﹣∠ACD=30°,
∵OC=OD,∠DOC=90°,
∴∠DCO=45°,
∴∠BCO=∠DCO﹣∠BCD=15°,
∵OB=OC,
∴∠CBO=∠BCO=15°,
∴∠BOC=150°,
∴∠DOB=∠BOC﹣∠DOC=150°﹣90°=60°,
∵OB=OD,
∴△BOD是等边三角形,
∴BD=OD=2.
故答案为2.
13.【答案】
解: ∵a+b2+|c-6|+28=4 +10b,
∴(a-1-4 +4)+(b2-10b+25)+|c-6|=0,
∴( -2)2+(b-5)2+|c-6|=0,
∴ ?2=0,b-5=0,c-6=0,
解得,a=5,b=5,c=6,
∴AC=BC=5,AB=6,
作CD⊥AB于点D,
则AD=3,CD=4,
设△ABC的外接圆的半径为r,
则OC=r,OD=4-r,OA=r,
∴32+(4-r)2=r2 ,
解得,r= ,
故答案为: .
三、解答题
14.【答案】证明:如图所示,取BC的中点F,连接DF,EF. ∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF.
∴E,B,C,D四点在以F点为圆心, BC为半径的圆上.
15.【答案】解:如图所示:
∵AB=AC=8,∠BAC=120°,O为△ABC外接圆的圆心,
∴AO⊥BC,
∴∠BAO=60°,
又∵OA=OB,
∴△ABO为等边三角形,
∴△ABC外接圆的半径为8.
16.【答案】证明:如图所示,取BC的中点F,连接DF,EF. ∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF.
∴E,B,C,D四点在以F点为圆心, ?BC为半径的圆上.
17.【答案】 解:(1)证明:如图1所示:∵O是等边△ABC的外心,∴∠1=∠2,∠3=∠4,∴AD=CD,∵四边形OADC为平行四边形,∴四边形OADC为菱形,∴BD垂直平分AC,∠4=∠5=∠6,而∠1=∠5,∴OA=OC,∠2=∠3,∴OB=OC,∴点O为△ABC的外心,∴△ABC为等边三角形,∴∠AOB=∠BOC=∠AOC=120°,BC=AC,∵四边形OADC为平行四边形,∴∠ADC=∠AOC=120°,AD=OC,CD=OA,∴AD=OB,在△BOC和△CDA中,, ∴△BOC≌△CDA(SAS);(2)解:作OH⊥AB于H,如图2所示,∵∠AOB=120°,OA=OB,∴∠BOH=(180°﹣120°)=30°,∵OH⊥AB,∴BH=AH=AB=, OH=BH=1,OB=2OH=2,∴S阴影部分=S扇形AOB﹣S△AOB=﹣××1=π﹣.
一、单选题
1.给定下列条件可以确定一个圆的是(?? )
A.?已知圆心??????????????????????B.?已知半径??????????????????????C.?已知直径??????????????????????D.?不在同一直线上三点
2.若三角形的外心在这个三角形的一边上,则这个三角形是(??? ).
A.?锐角三角形????????????????????????B.?直角三角形????????????????????????C.?钝角三角形????????????????????????D.?不能确定
3.三角形的外心具有的性质是( ???)
A.?到三边距离相等???????????B.?到三个顶点距离相等???????????C.?外心在三角形外???????????D.?外心在三角形内
4.下列条件中,能确定圆的是(? ?)
A.?以已知点O为圆心???????????????????????????????????????????????B.?以1cm长为半径
C.?经过已知点A,且半径为2cm??????????????????????????????D.?以点O为圆心,1cm为半径
5.如图为4×4的正方形网格,A,B,C,D,O均在格点上,点O是(?? )
A.?△ACD的外心????????????????????B.?△ABC的外心????????????????????C.?△ACD的内心????????????????????D.?△ABC的内心
6.如图,点O是△ABC的内切圆的圆心,若∠A=80°,则∠BOC为(? )
A.?100°?????????????????????????????????????B.?130°?????????????????????????????????????C.?50°?????????????????????????????????????D.?65°
7.已知:不在同一直线上的三点A,B,C
求作:⊙O,使它经过点A,B,C
作法:如图,
⑴连接AB ,作线段AB的垂直平分线DE;
⑵连接BC ,作线段BC的垂直平分线FG,交DE于点O;
⑶以O为圆心,OB 长为半径作⊙O.
⊙O就是所求作的圆.
根据以上作图过程及所作图形,下列结论中正确的是(?? )
A.?连接AC, 则点O是△ABC的内心????????????????????????????B.?
C.?连接OA,OC,则OA, OC不是⊙O的半径?????????????D.?若连接AC, 则点O在线段AC的垂直平分线上
8.现有如下4个命题:
①过两点可以作无数个圆.②三点可以确定一个圆.③任意一个三角形有且只有一个外接圆.④任意一个圆有且只有一个内接三角形.其中正确的有 ??
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
9.中,两条直角边的长分别是6cm和8cm,则 的外接圆的半径是________cm.
10.已知O为△ABC的外接圆圆心,若O在△ABC外,则△ABC是________(填“锐角三角形”或“直角三角形”或“钝角三角形”).
11.如图,在平面直角坐标系 中,点 的坐标分别是 是 的外接圆,则圆心 的坐标为________, 的半径为________.
12.已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.如果∠ACB=75°,圆O的半径为2,则BD的长为________.
13.已知△ABC的三边a,b,c,满足a+b2+|c﹣6|+28=4 +10b,则△ABC的外接圆半径=________.
三、解答题
14.如图所示,在△ABC中,CE,BD分别是AB,AC边上的高,求证:B,C,D,E四点在同一个圆上.
15.如图,已知等腰△ABC,AB=AC=8,∠BAC=120°,请用圆规和直尺作出△ABC的外接圆.并计算此外接圆的半径.
16.如图所示,BD,CE是△ABC的高,求证:E,B,C,D四点在同一个圆上.
17.如图,O是等边△ABC的外心,BO的延长线和⊙O相交于点D,连接DC,DA,OA,OC.
(1)求证:△BOC≌△CDA;
(2)若AB=, 求阴影部分的面积.
答案解析部分
一、单选题
1.【答案】 D
解:A、不能确定.因为半径不确定,故不符合题意;
B、不能确定.因为圆心的位置不确定,故不符合题意;
C、不能确定,因为圆心的位置不确定,故不符合题意;
D.不在同一直线上三点可以确定一个圆.故符合题意;
故答案为:D.
2.【答案】 B
解:∵根据圆周角定理:直径所对的圆周角是直角,
∴该三角形是直角三角形.
故答案为:B.
3.【答案】 B
解:三角形的外心是三角形三条垂直平分线的交点
∴外心到三角形的顶点的距离相等。
故答案为:B.
4.【答案】 D
解:∵圆心确定,半径确定后就可以确定圆,
∴D选项符合题意,
故答案为:D.
5.【答案】 B
解:由图可得:OA=OB=OC= ,
所以点O在△ABC的外心上,
故答案为:B.
6.【答案】 B
解:∵点O是△ABC的内切圆的圆心,∴∠OBC= ∠ABC,∠OCB= ∠ACB.
∵∠A=80°,∴∠ABC+∠ACB=180°﹣∠A=100°,∴∠OBC+∠OCB= (∠ABC+∠ACB)=50°,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣50°=130°.
故答案为:B.
7.【答案】 D
解:A:连接AC, 根据题意可知,点O是△ABC的外心,故 A不符合题意;
B: 根据题意无法证明 ,故 B不符合题意;
C: 连接OA,OC,则OA, OC是⊙O的半径,故 C不符合题意
D: 若连接AC, 则点O在线段AC的垂直平分线上,故 D符合题意
故答案为:D.
8.【答案】 B
解:①过两点可以作无数个圆,是真命题.
②不在同一直线上的三点可以确定一个圆,是假命题.
③任意一个三角形有且只有一个外接圆,是真命题.
④任意一个圆有无数个一个内接三角形,是假命题;
故选:
二、填空题
9.【答案】 5
解:由勾股定理得: 的斜边长为 ,
直角三角形的外接圆的圆心为斜边的中点,
的外接圆的半径为 ,
故答案为:5.
10.【答案】 钝角三角形
解:∵锐角三角形的外心在三角形的内部;直角三角形的外心为直角三角形斜边的中点;钝角三角形的外心在三角形的外部.
又∵O为△ABC的外接圆圆心,若O在△ABC外,
∴△ABC是钝角三角形,
故答案为:钝角三角形.
11.【答案】 (3,3);
解:∵点A,B,C的坐标分别是(0,2),(2,0),(4,0),
∴BC的垂直平分线为直线x=3,
∵OA=OB,
∴△OAB为等腰直角三角形,
∴AB的垂直平分线为第一、三象限的角平分线,即直线y=x,
∵直线x=3与直线y=x的交点为M点,
∴M点的坐标为(3,3),
∵ ,
∴⊙M的半径为 .
故答案为(3,3), .
12.【答案】 2
解:如图,
连接OB,
∵∠DOC=2∠ACD=90°.
∴∠ACD=45°,
∵∠ACB=75°,
∴∠BCD=∠ACB﹣∠ACD=30°,
∵OC=OD,∠DOC=90°,
∴∠DCO=45°,
∴∠BCO=∠DCO﹣∠BCD=15°,
∵OB=OC,
∴∠CBO=∠BCO=15°,
∴∠BOC=150°,
∴∠DOB=∠BOC﹣∠DOC=150°﹣90°=60°,
∵OB=OD,
∴△BOD是等边三角形,
∴BD=OD=2.
故答案为2.
13.【答案】
解: ∵a+b2+|c-6|+28=4 +10b,
∴(a-1-4 +4)+(b2-10b+25)+|c-6|=0,
∴( -2)2+(b-5)2+|c-6|=0,
∴ ?2=0,b-5=0,c-6=0,
解得,a=5,b=5,c=6,
∴AC=BC=5,AB=6,
作CD⊥AB于点D,
则AD=3,CD=4,
设△ABC的外接圆的半径为r,
则OC=r,OD=4-r,OA=r,
∴32+(4-r)2=r2 ,
解得,r= ,
故答案为: .
三、解答题
14.【答案】证明:如图所示,取BC的中点F,连接DF,EF. ∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF.
∴E,B,C,D四点在以F点为圆心, BC为半径的圆上.
15.【答案】解:如图所示:
∵AB=AC=8,∠BAC=120°,O为△ABC外接圆的圆心,
∴AO⊥BC,
∴∠BAO=60°,
又∵OA=OB,
∴△ABO为等边三角形,
∴△ABC外接圆的半径为8.
16.【答案】证明:如图所示,取BC的中点F,连接DF,EF. ∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF.
∴E,B,C,D四点在以F点为圆心, ?BC为半径的圆上.
17.【答案】 解:(1)证明:如图1所示:∵O是等边△ABC的外心,∴∠1=∠2,∠3=∠4,∴AD=CD,∵四边形OADC为平行四边形,∴四边形OADC为菱形,∴BD垂直平分AC,∠4=∠5=∠6,而∠1=∠5,∴OA=OC,∠2=∠3,∴OB=OC,∴点O为△ABC的外心,∴△ABC为等边三角形,∴∠AOB=∠BOC=∠AOC=120°,BC=AC,∵四边形OADC为平行四边形,∴∠ADC=∠AOC=120°,AD=OC,CD=OA,∴AD=OB,在△BOC和△CDA中,, ∴△BOC≌△CDA(SAS);(2)解:作OH⊥AB于H,如图2所示,∵∠AOB=120°,OA=OB,∴∠BOH=(180°﹣120°)=30°,∵OH⊥AB,∴BH=AH=AB=, OH=BH=1,OB=2OH=2,∴S阴影部分=S扇形AOB﹣S△AOB=﹣××1=π﹣.
