3.3 垂径定理 一课一练(含解析)
图片预览




文档简介
初中数学北师大版九年级下学期 第三章 3.3 垂径定理
一、单选题
1.如图,⊙O的弦AB=16,M是AB的中点,且OM=6,则⊙O的直径等于( )
A.?12?????????????????????????????????????????B.?16?????????????????????????????????????????C.?20?????????????????????????????????????????D.?24
2.如图,在⊙O中,直径EF⊥CD,垂足为M,若CD=2 ,EM=5,则⊙O的半径为(?? )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?6
3.一条排水管的截面如图所示,已知排水管的半径 ,水面宽 ,则截面圆心 到水面的距离 是(?? )
A.?2?????????????????????????????????????????B.?3?????????????????????????????????????????C.??????????????????????????????????????????D.?2.5
4.如图是一个半径为5cm的圆柱形输油管的横截面,若油面宽AB=8cm,则油面的深度为(?? )
A.?2cm?????????????????????????????????B.?2.5cm?????????????????????????????????C.?3cm?????????????????????????????????D.?3.5cm
5.如图,在⊙O中,弦AB长6cm,圆心O到AB的距离是3cm,⊙O的半径是(?? )
A.?3cm????????????????????????????????B.?3 cm????????????????????????????????C.?4cm????????????????????????????????D.?3 cm
6.已知⊙O的直径为10,圆心O到弦AB的距离OM为3,则弦AB的长是(?? )
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
7.如图,⊙O的直径AB=10,CD是⊙O的弦,CD⊥AB,垂足为E,且BE:AE=1:4,则CD的长为(??? )
A.?10??????????????????????????????????????????B.?12??????????????????????????????????????????C.?8??????????????????????????????????????????D.?9
8.如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
A.?4个???????????????????????????????????????B.?5个???????????????????????????????????????C.?6个???????????????????????????????????????D.?7个
二、填空题
9.如下图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C和D两点,AB=10cm,CD=6cm,则AC长为________cm.
10.如图,AB为圆O的弦,OC⊥AB,垂足为E,如果CE=2?,AB=8?,则圆O的半径为________.
11.运动会上,小捷掷出的铅球在场地上砸出一个小坑(图示是其主视图),其中AB为8cm,小坑的最大深度为3cm,则该铅球的半径为________cm.
12.如图,AB是 的直径,弦 于点E, , ,则 ________cm.
13.工程上常用钢珠来测量零件口宽,假设钢珠的直径是10mm,测得钢珠的顶端离零件表面的距离为8mm,如图所示,则这个零件的口宽AB的长度是________
三、解答题
14.⊙O的半径为5cm,弦AB=6cm,CD=8cm,且AB∥CD,求两弦之间的距离.
15.往直径为 的圆柱形油槽内装入一些油以后,截面如图所示,若油面宽 ,求油的最大深度.
16.如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有64m,即PN=4m时,试通过计算说明是否需要采取紧急措施。
17.如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端 分米, 为 中点, 为拱门最高点,圆心 在线段 上, 分米,求拱门所在圆的半径.
18.一些不便于直接测量的圆形孔道的直径可以用如下方法测量.如图,把一个直径为10mm的小钢球紧贴在孔道边缘,测得钢球顶端离孔道外端的距离为8mm.求这个孔道的直径AB .
答案解析部分
一、单选题
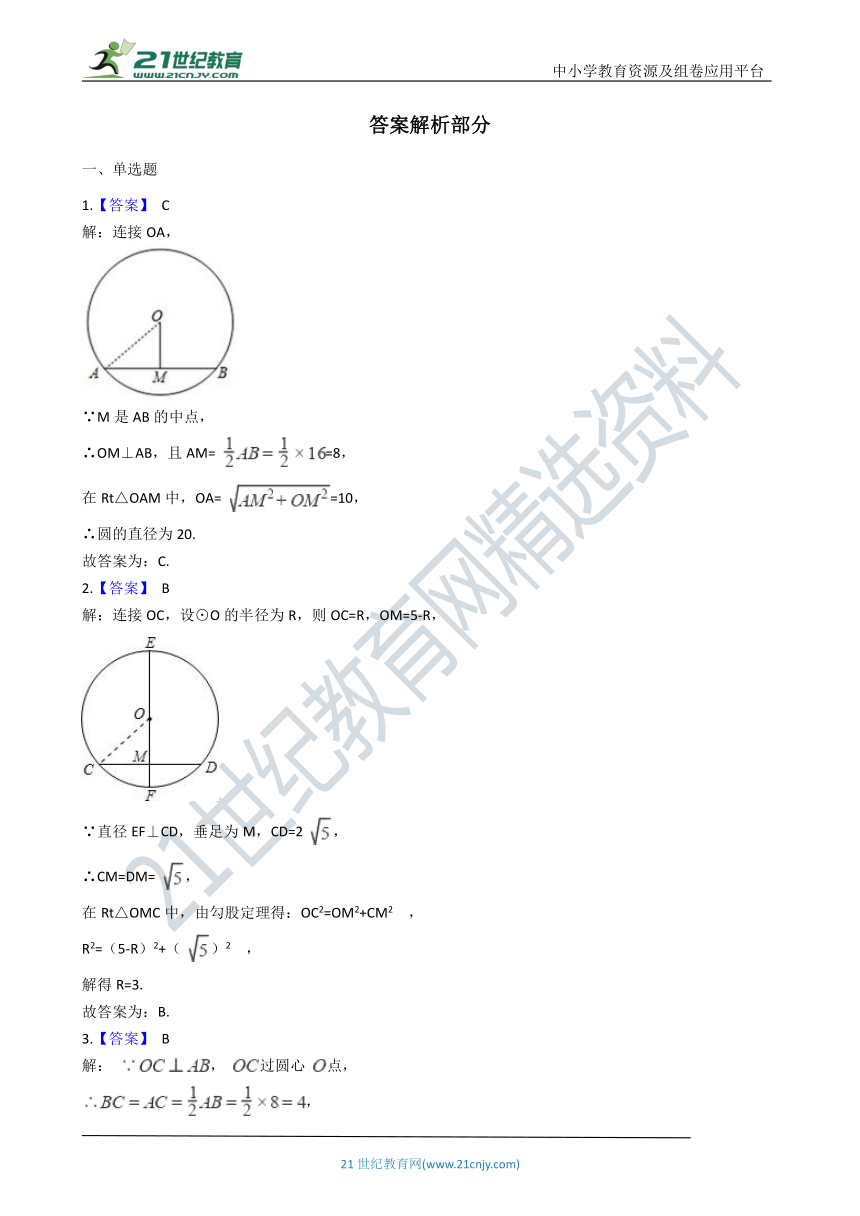
1.【答案】 C
解:连接OA,
∵M是AB的中点,
∴OM⊥AB,且AM= =8,
在Rt△OAM中,OA= =10,
∴圆的直径为20.
故答案为:C.
2.【答案】 B
解:连接OC,设⊙O的半径为R,则OC=R,OM=5-R,
∵直径EF⊥CD,垂足为M,CD=2 ,
∴CM=DM= ,
在Rt△OMC中,由勾股定理得:OC2=OM2+CM2 ,
R2=(5-R)2+( )2 ,
解得R=3.
故答案为:B.
3.【答案】 B
解: , 过圆心 点,
,
在 中,由勾股定理得: ,
故答案为:B.
4.【答案】 A
解:过点O作OD⊥AB于点D,
∵AB=8cm,
∴AD= AB=4cm,
在Rt△AOD中,OD= = =3(cm),
∴油面深度为:5-3=2(cm)
故答案为:A.
5.【答案】 B
解:如图所示,
由题意知 ,且 ,
,
,
则 .
故答案为: .
6.【答案】 D
解:连接OA,
∵⊙O的直径为10,
∴OA=5,
∵圆心O到弦AB的距离OM的长为3,
由垂径定理知,点M是AB的中点,AM= AB,
由勾股定理可得,AM= =4,
所以AB=2AM=8.
故答案为:D.
7.【答案】 A
解:连接OC
∵ BE:AE=1:4?,设BE=x,AE=4x
∴AB= BE+AE=5x
∵ AB=10
∴5x=10,即x=2
∵OC=OB=5
∴OE=OB-BE=5-2=3
∴在Rt△OCE中,
∴
∴CD=2CE=8
故答案为:C
8.【答案】 D
解:当P为AB的中点时,利用垂径定理得到OP⊥AB,此时OP最短,
∵AB=16,∴AP=BP=8,
在直角三角形AOP中,OA=10,AP=8,
根据勾股定理得:OP= = =6,即OP的最小值为6;
当P与A或B重合时,OP最长,此时OP=10,
∴6≤OP<10,
则使线段OP的长度为整数,
∴OP=6,7,8,9
根据对称性可知,满足条件的点P的个数有7个
故答案为:D.
二、填空题
9.【答案】 2
解:过O作OE⊥AB,垂足为E,
根据垂径定理,AE= AB= ×10=5cm,
CE= CD= ×6=3cm,
∴AC=AE﹣CE=5﹣3=2cm,
故答案为:2.
10.【答案】
解:如图,连接OA;
设OA=OC=x,则OE=OC-CE=x-2?;
∵OC⊥AB,
∴AE=BE= ;
在Rt△AOE中:?? ,
解得:??
故答案为:.
11.【答案】
解:如图所示:作OD⊥AB于D,
∵AB=8cm,OD⊥AB,小坑的最大深度为3cm,
∴AD= AB=4cm.
设OA=rcm,则OD=(r?3)cm,
在Rt△OAD中,OA2=OD2+AD2 , 即r2=(r?3)2+42 ,
解得r= ,即该铅球的半径为 cm,
故答案为 .
12.【答案】 9
解: ,AB是直径,
,
在 中, ,
,
故答案为9.
13.【答案】 8 mm
解:连接OA,过点O作OD⊥AB于点D,
则AB=2AD,
∵钢珠的直径是10mm,
∴钢珠的半径是5mm,
∵钢珠顶端离零件表面的距离为8mm,
∴OD=3mm,
在Rt△AOD中,
∵AD= mm,
∴AB=2AD=2×4=8mm.
故答案为:8 mm.
三、解答题
14.【答案】 解:如图:过点O作OE⊥AB于E,交CD于F,
∵AB∥CD,
∴OF⊥CD,
∵OE过圆心,OE⊥AB,
∴EB= AB=3cm,
∵OB=5cm,
∴EO=4cm,
同理,OF=3cm,
∴EF=4-3=1cm,
当AB、CD位于圆心两旁时EF=4+3=7cm,
∴EF=1cm或EF=7cm.
15.【答案】 解:过点O作OC⊥AB于点D,交弧AB于点C.
∵OC⊥AB于点D
∴BD= AB= ×60=30cm,
∵⊙O的直径为68cm
∴OB=OC=34cm
∵在Rt△ODB中,OD= (cm),
∴DC=OC﹣OD=34﹣16=18(cm);
答:油的最大深度为18cm.
16.【答案】 解:设圆弧所在圆的圆心为O,连结OA,OA',如图所示
设半径为x(m)则OA=OA’=OP=x(m)
由垂径定理可知AM=BM? A’N=B’N
∵AB=60m,∴AM=30m,且OM=OP-PM=(x-18)m
在Rt△AOM中,由勾股定理可得AO2=OM2+AM2
即x2=(x-18)2+302 , 解得x=34
∴ON=OP-PN=34-4=30(m)
在△A'ON中,由勾股定理可得
A'N= = =16(m)
A'B'=32m>30m
∴不需要采取紧急措施。
17.【答案】 解:连接
过圆心, 为 中点,
,
为 中点,
,
设半径为 分米,则 ,
,
,
在 中, ,
,
.
拱门所在圆的半径是 分米.
18.【答案】 解:连接OA,过点O作OD⊥AB于点D,
则AB=2AD,
∵钢珠的直径是10mm,
∴钢珠的半径是5mm,
∵钢珠顶端离零件表面的距离为8mm,
∴OD=3mm,
在Rt△AOD中,
∵AD= =4mm,
∴AB=2AD=2×4=8mm.
答:这个孔道的直径为8mm.
一、单选题
1.如图,⊙O的弦AB=16,M是AB的中点,且OM=6,则⊙O的直径等于( )
A.?12?????????????????????????????????????????B.?16?????????????????????????????????????????C.?20?????????????????????????????????????????D.?24
2.如图,在⊙O中,直径EF⊥CD,垂足为M,若CD=2 ,EM=5,则⊙O的半径为(?? )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?6
3.一条排水管的截面如图所示,已知排水管的半径 ,水面宽 ,则截面圆心 到水面的距离 是(?? )
A.?2?????????????????????????????????????????B.?3?????????????????????????????????????????C.??????????????????????????????????????????D.?2.5
4.如图是一个半径为5cm的圆柱形输油管的横截面,若油面宽AB=8cm,则油面的深度为(?? )
A.?2cm?????????????????????????????????B.?2.5cm?????????????????????????????????C.?3cm?????????????????????????????????D.?3.5cm
5.如图,在⊙O中,弦AB长6cm,圆心O到AB的距离是3cm,⊙O的半径是(?? )
A.?3cm????????????????????????????????B.?3 cm????????????????????????????????C.?4cm????????????????????????????????D.?3 cm
6.已知⊙O的直径为10,圆心O到弦AB的距离OM为3,则弦AB的长是(?? )
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
7.如图,⊙O的直径AB=10,CD是⊙O的弦,CD⊥AB,垂足为E,且BE:AE=1:4,则CD的长为(??? )
A.?10??????????????????????????????????????????B.?12??????????????????????????????????????????C.?8??????????????????????????????????????????D.?9
8.如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
A.?4个???????????????????????????????????????B.?5个???????????????????????????????????????C.?6个???????????????????????????????????????D.?7个
二、填空题
9.如下图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C和D两点,AB=10cm,CD=6cm,则AC长为________cm.
10.如图,AB为圆O的弦,OC⊥AB,垂足为E,如果CE=2?,AB=8?,则圆O的半径为________.
11.运动会上,小捷掷出的铅球在场地上砸出一个小坑(图示是其主视图),其中AB为8cm,小坑的最大深度为3cm,则该铅球的半径为________cm.
12.如图,AB是 的直径,弦 于点E, , ,则 ________cm.
13.工程上常用钢珠来测量零件口宽,假设钢珠的直径是10mm,测得钢珠的顶端离零件表面的距离为8mm,如图所示,则这个零件的口宽AB的长度是________
三、解答题
14.⊙O的半径为5cm,弦AB=6cm,CD=8cm,且AB∥CD,求两弦之间的距离.
15.往直径为 的圆柱形油槽内装入一些油以后,截面如图所示,若油面宽 ,求油的最大深度.
16.如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有64m,即PN=4m时,试通过计算说明是否需要采取紧急措施。
17.如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端 分米, 为 中点, 为拱门最高点,圆心 在线段 上, 分米,求拱门所在圆的半径.
18.一些不便于直接测量的圆形孔道的直径可以用如下方法测量.如图,把一个直径为10mm的小钢球紧贴在孔道边缘,测得钢球顶端离孔道外端的距离为8mm.求这个孔道的直径AB .
答案解析部分
一、单选题
1.【答案】 C
解:连接OA,
∵M是AB的中点,
∴OM⊥AB,且AM= =8,
在Rt△OAM中,OA= =10,
∴圆的直径为20.
故答案为:C.
2.【答案】 B
解:连接OC,设⊙O的半径为R,则OC=R,OM=5-R,
∵直径EF⊥CD,垂足为M,CD=2 ,
∴CM=DM= ,
在Rt△OMC中,由勾股定理得:OC2=OM2+CM2 ,
R2=(5-R)2+( )2 ,
解得R=3.
故答案为:B.
3.【答案】 B
解: , 过圆心 点,
,
在 中,由勾股定理得: ,
故答案为:B.
4.【答案】 A
解:过点O作OD⊥AB于点D,
∵AB=8cm,
∴AD= AB=4cm,
在Rt△AOD中,OD= = =3(cm),
∴油面深度为:5-3=2(cm)
故答案为:A.
5.【答案】 B
解:如图所示,
由题意知 ,且 ,
,
,
则 .
故答案为: .
6.【答案】 D
解:连接OA,
∵⊙O的直径为10,
∴OA=5,
∵圆心O到弦AB的距离OM的长为3,
由垂径定理知,点M是AB的中点,AM= AB,
由勾股定理可得,AM= =4,
所以AB=2AM=8.
故答案为:D.
7.【答案】 A
解:连接OC
∵ BE:AE=1:4?,设BE=x,AE=4x
∴AB= BE+AE=5x
∵ AB=10
∴5x=10,即x=2
∵OC=OB=5
∴OE=OB-BE=5-2=3
∴在Rt△OCE中,
∴
∴CD=2CE=8
故答案为:C
8.【答案】 D
解:当P为AB的中点时,利用垂径定理得到OP⊥AB,此时OP最短,
∵AB=16,∴AP=BP=8,
在直角三角形AOP中,OA=10,AP=8,
根据勾股定理得:OP= = =6,即OP的最小值为6;
当P与A或B重合时,OP最长,此时OP=10,
∴6≤OP<10,
则使线段OP的长度为整数,
∴OP=6,7,8,9
根据对称性可知,满足条件的点P的个数有7个
故答案为:D.
二、填空题
9.【答案】 2
解:过O作OE⊥AB,垂足为E,
根据垂径定理,AE= AB= ×10=5cm,
CE= CD= ×6=3cm,
∴AC=AE﹣CE=5﹣3=2cm,
故答案为:2.
10.【答案】
解:如图,连接OA;
设OA=OC=x,则OE=OC-CE=x-2?;
∵OC⊥AB,
∴AE=BE= ;
在Rt△AOE中:?? ,
解得:??
故答案为:.
11.【答案】
解:如图所示:作OD⊥AB于D,
∵AB=8cm,OD⊥AB,小坑的最大深度为3cm,
∴AD= AB=4cm.
设OA=rcm,则OD=(r?3)cm,
在Rt△OAD中,OA2=OD2+AD2 , 即r2=(r?3)2+42 ,
解得r= ,即该铅球的半径为 cm,
故答案为 .
12.【答案】 9
解: ,AB是直径,
,
在 中, ,
,
故答案为9.
13.【答案】 8 mm
解:连接OA,过点O作OD⊥AB于点D,
则AB=2AD,
∵钢珠的直径是10mm,
∴钢珠的半径是5mm,
∵钢珠顶端离零件表面的距离为8mm,
∴OD=3mm,
在Rt△AOD中,
∵AD= mm,
∴AB=2AD=2×4=8mm.
故答案为:8 mm.
三、解答题
14.【答案】 解:如图:过点O作OE⊥AB于E,交CD于F,
∵AB∥CD,
∴OF⊥CD,
∵OE过圆心,OE⊥AB,
∴EB= AB=3cm,
∵OB=5cm,
∴EO=4cm,
同理,OF=3cm,
∴EF=4-3=1cm,
当AB、CD位于圆心两旁时EF=4+3=7cm,
∴EF=1cm或EF=7cm.
15.【答案】 解:过点O作OC⊥AB于点D,交弧AB于点C.
∵OC⊥AB于点D
∴BD= AB= ×60=30cm,
∵⊙O的直径为68cm
∴OB=OC=34cm
∵在Rt△ODB中,OD= (cm),
∴DC=OC﹣OD=34﹣16=18(cm);
答:油的最大深度为18cm.
16.【答案】 解:设圆弧所在圆的圆心为O,连结OA,OA',如图所示
设半径为x(m)则OA=OA’=OP=x(m)
由垂径定理可知AM=BM? A’N=B’N
∵AB=60m,∴AM=30m,且OM=OP-PM=(x-18)m
在Rt△AOM中,由勾股定理可得AO2=OM2+AM2
即x2=(x-18)2+302 , 解得x=34
∴ON=OP-PN=34-4=30(m)
在△A'ON中,由勾股定理可得
A'N= = =16(m)
A'B'=32m>30m
∴不需要采取紧急措施。
17.【答案】 解:连接
过圆心, 为 中点,
,
为 中点,
,
设半径为 分米,则 ,
,
,
在 中, ,
,
.
拱门所在圆的半径是 分米.
18.【答案】 解:连接OA,过点O作OD⊥AB于点D,
则AB=2AD,
∵钢珠的直径是10mm,
∴钢珠的半径是5mm,
∵钢珠顶端离零件表面的距离为8mm,
∴OD=3mm,
在Rt△AOD中,
∵AD= =4mm,
∴AB=2AD=2×4=8mm.
答:这个孔道的直径为8mm.
