2020—2021学年苏科版数学八年级下册 专题训练(三)特殊平行四边形中的折叠问题(word版含答案)
文档属性
| 名称 | 2020—2021学年苏科版数学八年级下册 专题训练(三)特殊平行四边形中的折叠问题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 203.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 00:00:00 | ||
图片预览





文档简介
专题训练(三) 特殊平行四边形中的折叠问题
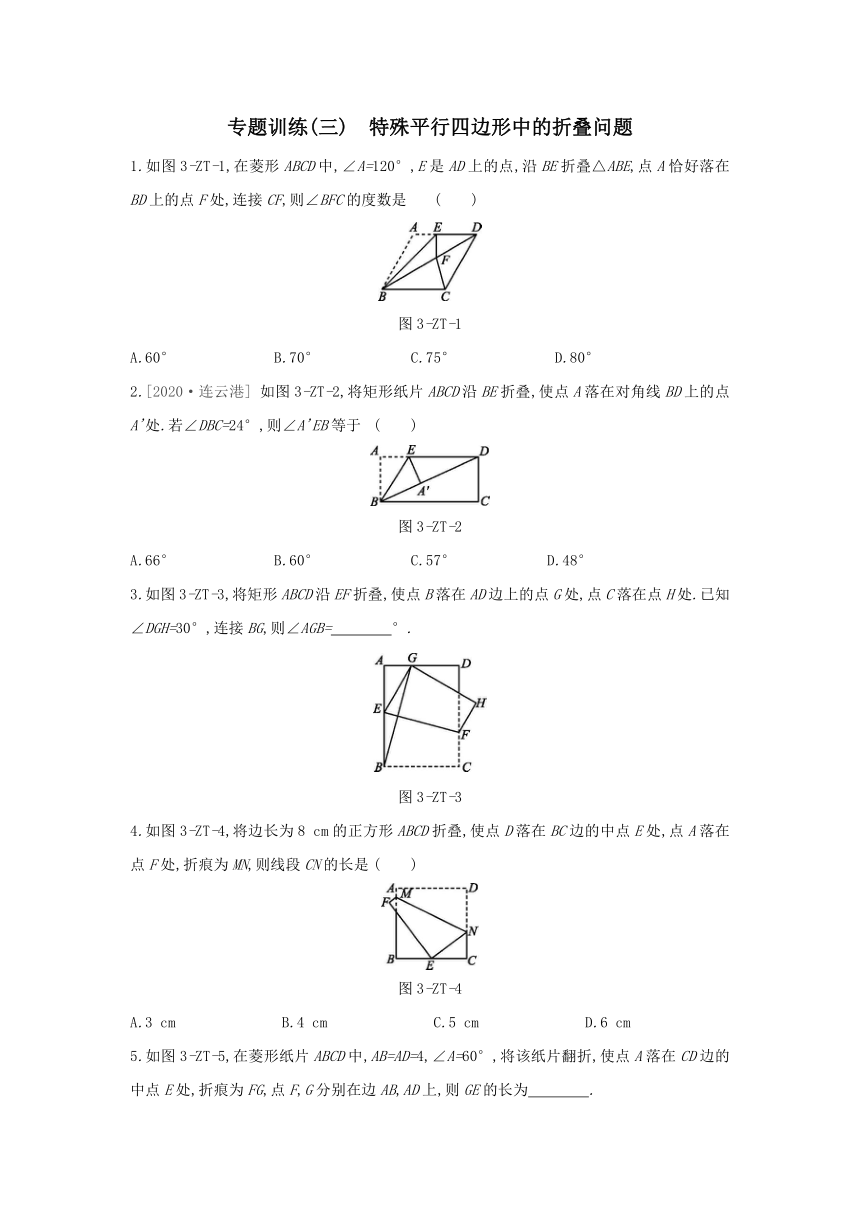
1.如图3-ZT-1,在菱形ABCD中,∠A=120°,E是AD上的点,沿BE折叠△ABE,点A恰好落在BD上的点F处,连接CF,则∠BFC的度数是
( )
图3-ZT-1
A.60°
B.70°
C.75°
D.80°
2.[2020·连云港]
如图3-ZT-2,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的点A'处.若∠DBC=24°,则∠A'EB等于
( )
图3-ZT-2
A.66°
B.60°
C.57°
D.48°
3.如图3-ZT-3,将矩形ABCD沿EF折叠,使点B落在AD边上的点G处,点C落在点H处.已知∠DGH=30°,连接BG,则∠AGB= °.?
图3-ZT-3
4.如图3-ZT-4,将边长为8
cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则线段CN的长是
( )
图3-ZT-4
A.3
cm
B.4
cm
C.5
cm
D.6
cm
5.如图3-ZT-5,在菱形纸片ABCD中,AB=AD=4,∠A=60°,将该纸片翻折,使点A落在CD边的中点E处,折痕为FG,点F,G分别在边AB,AD上,则GE的长为 .?
图3-ZT-5
6.把一张矩形纸片ABCD按图3-ZT-6所示的方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.
(1)求证:△BEH≌△DFG;
(2)若AB=6
cm,BC=8
cm,求线段FG的长.
图3-ZT-6
7.如图3-ZT-7,在矩形ABCD中,AB=8,BC=4,将矩形ABCD沿AC折叠,则重叠部分△AFC的面积为
( )
图3-ZT-7
A.12
B.10
C.8
D.6
8.[2019·长春]
如图3-ZT-8,有一张矩形纸片ABCD,AB=8,AD=6.先将矩形纸片ABCD折叠,使边AD落在边AB上,点D落在点E处,折痕为AF;再将△AEF沿EF折叠,AF与BC相交于点G,则△GCF的周长为 .?
图3-ZT-8
9.[2019·滨州]
如图3-ZT-9,在矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.
(1)求证:四边形CEFG是菱形;
(2)若AB=6,AD=10,求四边形CEFG的面积.
图3-ZT-9
10.[2019·桂林]
将矩形ABCD按如图3-ZT-10所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则的值为
( )
图3-ZT-10
A.
B.
C.
D.
11.如图3-ZT-11,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=AB,将矩形ABCD沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是
( )
图3-ZT-11
A.①②
B.②③
C.①③
D.①④
12.已知:如图3-ZT-12,现有一张边长为4的正方形纸片ABCD,P为正方形的边AD上的一点(不与点A,D重合),将正方形纸片ABCD折叠,使点B落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接BP,BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?请判断并证明你的结论.
图3-ZT-12
13.[2019·盐城]
如图3-ZT-13①所示是一张矩形纸片,按以下步骤进行操作:
(Ⅰ)将矩形纸片沿DF折叠,使点A落在CD边上的点E处,如图②;
(Ⅱ)在第一次折叠的基础上,过点C再次折叠,使得点B落在边CD上的点B'处,如图③,两次折痕交于点O;
(Ⅲ)展开纸片,分别连接OB,OE,OC,如图④.
【探究】
(1)求证:△OBC≌△OED;
(2)若AB=8,设BC为x,OB2为y,求y关于x的关系式(不必写出自变量的取值范围).
图3-ZT-13
1.C [解析]
∵四边形ABCD是菱形,
∴AB=BC,∠A+∠ABC=180°,BD平分∠ABC.
∵∠A=120°,∴∠ABC=60°,
∴∠FBC=30°.
根据折叠的性质可得AB=BF,∴FB=BC,
∴∠BFC=∠BCF=(180°-30°)÷2=75°.
故选C.
2.C [解析]
由折叠的性质可得△BAE≌△BA'E,所以∠ABE=∠A'BE,∠EAB=∠EA'B.由矩形ABCD可得∠ABC=∠BAE=90°,且题目中已知∠DBC=24°,可以得到∠ABE=∠A'BE=33°,所以∠A'EB=180°-∠A'BE-∠EA'B=57°.故选C.
3.75 [解析]
由折叠的性质可知GE=BE,∠EGH=∠ABC=90°,∠EBG=∠EGB,∴∠EGH-∠EGB=∠EBC-∠EBG,
即∠GBC=∠BGH.
∵AD∥BC,∴∠AGB=∠GBC,
∴∠AGB=∠BGH,
∵∠DGH=30°,∴∠AGH=150°,
∴∠AGB=∠AGH=75°.
4.A [解析]
设CN=x
cm,则DN=(8-x)cm,由折叠的性质,知EN=DN=(8-x)cm,
而EC=BC=4
cm.在Rt△ECN中,由勾股定理,可知EN2=EC2+CN2,即(8-x)2=16+x2,整理,得16x=48,解得x=3.故选A.
5.2.8 [解析]
如图,过点E作EH⊥AD交AD的延长线于点H.
∵四边形ABCD是菱形,
∴AB∥CD,AD=AB=CD=4,
∴∠HDE=∠A=60°.
∵E是CD的中点,∴DE=CD=2.
在Rt△DHE中,DE=2,HE⊥DH,∠HDE=60°,
∴DH=DE=1,HE===,
由折叠的性质可得,AG=GE,
∴在Rt△HGE中,GH=AD-AG+DH=4-GE+1=5-GE,
由勾股定理,得GE2=GH2+HE2,
即GE2=(5-GE)2+3,
解得GE=2.8.
6.[解析]
(1)如图,先根据矩形的性质得出∠ABD=∠BDC,再由图形折叠的性质得出∠1=∠2,∠3=∠4,∠A=∠BEH=90°,∠C=∠DFG=90°,进而可得出△BEH≌△DFG;
(2)先根据勾股定理得出BD的长,进而得出BF的长,由图形翻折变换的性质得出CG=FG,设FG=x
cm,则BG=(8-x)cm,再利用勾股定理即可求出x的值.
解:(1)证明:如图.
∵四边形ABCD是矩形,
∴AB=CD,∠A=∠C=90°,AB∥CD,
∴∠ABD=∠BDC.
∵△BEH是由△BAH翻折而成的,
∴∠1=∠2,∠A=∠HEB=90°,AB=BE.
∵△DGF是由△DGC翻折而成的,
∴∠3=∠4,∠C=∠DFG=90°,CD=DF,
∴∠2=∠3,BE=DF.
在△BEH和△DFG中,
∴△BEH≌△DFG.
(2)∵四边形ABCD是矩形,AB=6
cm,BC=8
cm,∴AB=CD=6
cm,
∴BD===10(cm).
由(1)知DF=CD,CG=FG,
∴BF=10-6=4(cm).
设FG=x
cm,则BG=(8-x)cm.
在Rt△BGF中,BG2=BF2+FG2,
即(8-x)2=42+x2,
解得x=3,即FG=3
cm.
7.B [解析]
依题意可证得△AD'F≌△CBF,
∴△AD'F与△CBF的面积相等.
设BF=x,则在Rt△AD'F中,(8-x)2=x2+42,解得x=3,∴AF=5,
∴S△AFC=×5×4=10.
8.4+2 [解析]
由折叠的性质可知∠A=45°,AD=DF,
∴FC=2,∠AFC=45°,
∴CG=2,∴FG=2,
∴△GCF的周长为4+2.
9.解:(1)证明:由题意可得,△BCE≌△BFE,
∴∠BEC=∠BEF,FE=CE.
∵FG∥CE,∴∠FGE=∠BEC,
∴∠FGE=∠FEG,
∴FG=FE,∴FG=CE.
又∵FG∥CE,∴四边形CEFG是平行四边形.
又∵FE=CE,∴四边形CEFG是菱形.
(2)∵在矩形ABCD中,AB=6,AD=10,BC=BF,
∴∠BAF=∠D=90°,AD=BC=BF=10,
∴AF=8,∴DF=2.
设EF=x,则CE=x,DE=6-x.
在Rt△DEF中,有EF2=DF2+DE2,
∴22+(6-x)2=x2,
解得x=,∴CE=,
∴四边形CEFG的面积是CE·DF=×2=.
10.B [解析]
由折叠的性质可得AE=OE=DE,CG=OG=DG,
∴E,G分别为AD,CD的中点.
设CD=2a,AD=2b,
则AB=2a=OB,DG=OG=CG=a,BG=3a,BC=AD=2b.
∵∠C=90°,
∴在Rt△BCG中,CG2+BC2=BG2,
即a2+(2b)2=(3a)2,
∴b2=2a2,即b=a,
∴=,∴的值为.
故选B.
11.D [解析]
∵AE=AB,∴BE=2AE.
由翻折的性质,得PE=BE,∴PE=2AE,
∴∠APE=30°,∴∠AEP=90°-30°=60°,
∴∠BEF=(180°-∠AEP)=×(180°-60°)=60°,
∴∠EFB=90°-60°=30°,
∴EF=2BE,故①正确;
∵BE=PE,∴EF=2PE.
∵EF>PF,
∴PF<2PE,故②错误;
由翻折的性质,得EF⊥PB,
∴∠EBQ=∠EFB=30°,
∴BE=2EQ,EF=2BE,
∴FQ=3EQ,故③错误;
由翻折的性质,得∠EFB=∠EFP=30°,
且BF=PF,
∴∠BFP=30°+30°=60°,
∴△PBF是等边三角形,故④正确.
综上所述,正确的结论是①④.故选D.
12.解:(1)证明:由折叠的性质,得PE=BE,
∴∠EBP=∠EPB.
由题易知∠EPH=∠EBC=90°,
∴∠EPH-∠EPB=∠EBC-∠EBP,
即∠PBC=∠BPH.
由题易知AD∥BC,
∴∠APB=∠PBC,∴∠APB=∠BPH.
(2)△PDH的周长不变,为定值8.
证明:过点B作BQ⊥PH,垂足为Q.
由(1)知∠APB=∠BPH.
在△ABP和△QBP中,
∴△ABP≌△QBP(AAS),
∴AP=QP,AB=QB.
由题易知AB=BC,
∴BC=QB.
又由题易知∠C=∠BQH=90°,
∴△BCH和△BQH均为直角三角形.
又∵BH=BH,
∴Rt△BCH≌Rt△BQH,
∴CH=QH,
故△PDH的周长为PD+DH+PH=AP+PD+DH+HC=AD+CD=8.
13.解:(1)证明:由折叠的性质,得AD=DE,∠BCO=∠DCO=∠ADO=∠CDO=45°,
∴BC=DE,∠COD=90°,OC=OD.
在△OBC和△OED中,
∴△OBC≌△OED(SAS).
(2)如图,过点O作OH⊥CD于点H.
由(1)得△OBC≌△OED,∴OE=OB.
∵BC=x,∴AD=DE=x,
∴CE=8-x.
∵OC=OD,∠COD=90°,
∴CH=CD=AB=×8=4,OH=
CD=4,
∴EH=CH-CE=4-(8-x)=x-4.
在Rt△OHE中,由勾股定理得OE2=OH2+EH2,
即OB2=42+(x-4)2,
∴y关于x的关系式为y=x2-8x+32.
1.如图3-ZT-1,在菱形ABCD中,∠A=120°,E是AD上的点,沿BE折叠△ABE,点A恰好落在BD上的点F处,连接CF,则∠BFC的度数是
( )
图3-ZT-1
A.60°
B.70°
C.75°
D.80°
2.[2020·连云港]
如图3-ZT-2,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的点A'处.若∠DBC=24°,则∠A'EB等于
( )
图3-ZT-2
A.66°
B.60°
C.57°
D.48°
3.如图3-ZT-3,将矩形ABCD沿EF折叠,使点B落在AD边上的点G处,点C落在点H处.已知∠DGH=30°,连接BG,则∠AGB= °.?
图3-ZT-3
4.如图3-ZT-4,将边长为8
cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则线段CN的长是
( )
图3-ZT-4
A.3
cm
B.4
cm
C.5
cm
D.6
cm
5.如图3-ZT-5,在菱形纸片ABCD中,AB=AD=4,∠A=60°,将该纸片翻折,使点A落在CD边的中点E处,折痕为FG,点F,G分别在边AB,AD上,则GE的长为 .?
图3-ZT-5
6.把一张矩形纸片ABCD按图3-ZT-6所示的方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.
(1)求证:△BEH≌△DFG;
(2)若AB=6
cm,BC=8
cm,求线段FG的长.
图3-ZT-6
7.如图3-ZT-7,在矩形ABCD中,AB=8,BC=4,将矩形ABCD沿AC折叠,则重叠部分△AFC的面积为
( )
图3-ZT-7
A.12
B.10
C.8
D.6
8.[2019·长春]
如图3-ZT-8,有一张矩形纸片ABCD,AB=8,AD=6.先将矩形纸片ABCD折叠,使边AD落在边AB上,点D落在点E处,折痕为AF;再将△AEF沿EF折叠,AF与BC相交于点G,则△GCF的周长为 .?
图3-ZT-8
9.[2019·滨州]
如图3-ZT-9,在矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.
(1)求证:四边形CEFG是菱形;
(2)若AB=6,AD=10,求四边形CEFG的面积.
图3-ZT-9
10.[2019·桂林]
将矩形ABCD按如图3-ZT-10所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则的值为
( )
图3-ZT-10
A.
B.
C.
D.
11.如图3-ZT-11,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=AB,将矩形ABCD沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是
( )
图3-ZT-11
A.①②
B.②③
C.①③
D.①④
12.已知:如图3-ZT-12,现有一张边长为4的正方形纸片ABCD,P为正方形的边AD上的一点(不与点A,D重合),将正方形纸片ABCD折叠,使点B落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接BP,BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?请判断并证明你的结论.
图3-ZT-12
13.[2019·盐城]
如图3-ZT-13①所示是一张矩形纸片,按以下步骤进行操作:
(Ⅰ)将矩形纸片沿DF折叠,使点A落在CD边上的点E处,如图②;
(Ⅱ)在第一次折叠的基础上,过点C再次折叠,使得点B落在边CD上的点B'处,如图③,两次折痕交于点O;
(Ⅲ)展开纸片,分别连接OB,OE,OC,如图④.
【探究】
(1)求证:△OBC≌△OED;
(2)若AB=8,设BC为x,OB2为y,求y关于x的关系式(不必写出自变量的取值范围).
图3-ZT-13
1.C [解析]
∵四边形ABCD是菱形,
∴AB=BC,∠A+∠ABC=180°,BD平分∠ABC.
∵∠A=120°,∴∠ABC=60°,
∴∠FBC=30°.
根据折叠的性质可得AB=BF,∴FB=BC,
∴∠BFC=∠BCF=(180°-30°)÷2=75°.
故选C.
2.C [解析]
由折叠的性质可得△BAE≌△BA'E,所以∠ABE=∠A'BE,∠EAB=∠EA'B.由矩形ABCD可得∠ABC=∠BAE=90°,且题目中已知∠DBC=24°,可以得到∠ABE=∠A'BE=33°,所以∠A'EB=180°-∠A'BE-∠EA'B=57°.故选C.
3.75 [解析]
由折叠的性质可知GE=BE,∠EGH=∠ABC=90°,∠EBG=∠EGB,∴∠EGH-∠EGB=∠EBC-∠EBG,
即∠GBC=∠BGH.
∵AD∥BC,∴∠AGB=∠GBC,
∴∠AGB=∠BGH,
∵∠DGH=30°,∴∠AGH=150°,
∴∠AGB=∠AGH=75°.
4.A [解析]
设CN=x
cm,则DN=(8-x)cm,由折叠的性质,知EN=DN=(8-x)cm,
而EC=BC=4
cm.在Rt△ECN中,由勾股定理,可知EN2=EC2+CN2,即(8-x)2=16+x2,整理,得16x=48,解得x=3.故选A.
5.2.8 [解析]
如图,过点E作EH⊥AD交AD的延长线于点H.
∵四边形ABCD是菱形,
∴AB∥CD,AD=AB=CD=4,
∴∠HDE=∠A=60°.
∵E是CD的中点,∴DE=CD=2.
在Rt△DHE中,DE=2,HE⊥DH,∠HDE=60°,
∴DH=DE=1,HE===,
由折叠的性质可得,AG=GE,
∴在Rt△HGE中,GH=AD-AG+DH=4-GE+1=5-GE,
由勾股定理,得GE2=GH2+HE2,
即GE2=(5-GE)2+3,
解得GE=2.8.
6.[解析]
(1)如图,先根据矩形的性质得出∠ABD=∠BDC,再由图形折叠的性质得出∠1=∠2,∠3=∠4,∠A=∠BEH=90°,∠C=∠DFG=90°,进而可得出△BEH≌△DFG;
(2)先根据勾股定理得出BD的长,进而得出BF的长,由图形翻折变换的性质得出CG=FG,设FG=x
cm,则BG=(8-x)cm,再利用勾股定理即可求出x的值.
解:(1)证明:如图.
∵四边形ABCD是矩形,
∴AB=CD,∠A=∠C=90°,AB∥CD,
∴∠ABD=∠BDC.
∵△BEH是由△BAH翻折而成的,
∴∠1=∠2,∠A=∠HEB=90°,AB=BE.
∵△DGF是由△DGC翻折而成的,
∴∠3=∠4,∠C=∠DFG=90°,CD=DF,
∴∠2=∠3,BE=DF.
在△BEH和△DFG中,
∴△BEH≌△DFG.
(2)∵四边形ABCD是矩形,AB=6
cm,BC=8
cm,∴AB=CD=6
cm,
∴BD===10(cm).
由(1)知DF=CD,CG=FG,
∴BF=10-6=4(cm).
设FG=x
cm,则BG=(8-x)cm.
在Rt△BGF中,BG2=BF2+FG2,
即(8-x)2=42+x2,
解得x=3,即FG=3
cm.
7.B [解析]
依题意可证得△AD'F≌△CBF,
∴△AD'F与△CBF的面积相等.
设BF=x,则在Rt△AD'F中,(8-x)2=x2+42,解得x=3,∴AF=5,
∴S△AFC=×5×4=10.
8.4+2 [解析]
由折叠的性质可知∠A=45°,AD=DF,
∴FC=2,∠AFC=45°,
∴CG=2,∴FG=2,
∴△GCF的周长为4+2.
9.解:(1)证明:由题意可得,△BCE≌△BFE,
∴∠BEC=∠BEF,FE=CE.
∵FG∥CE,∴∠FGE=∠BEC,
∴∠FGE=∠FEG,
∴FG=FE,∴FG=CE.
又∵FG∥CE,∴四边形CEFG是平行四边形.
又∵FE=CE,∴四边形CEFG是菱形.
(2)∵在矩形ABCD中,AB=6,AD=10,BC=BF,
∴∠BAF=∠D=90°,AD=BC=BF=10,
∴AF=8,∴DF=2.
设EF=x,则CE=x,DE=6-x.
在Rt△DEF中,有EF2=DF2+DE2,
∴22+(6-x)2=x2,
解得x=,∴CE=,
∴四边形CEFG的面积是CE·DF=×2=.
10.B [解析]
由折叠的性质可得AE=OE=DE,CG=OG=DG,
∴E,G分别为AD,CD的中点.
设CD=2a,AD=2b,
则AB=2a=OB,DG=OG=CG=a,BG=3a,BC=AD=2b.
∵∠C=90°,
∴在Rt△BCG中,CG2+BC2=BG2,
即a2+(2b)2=(3a)2,
∴b2=2a2,即b=a,
∴=,∴的值为.
故选B.
11.D [解析]
∵AE=AB,∴BE=2AE.
由翻折的性质,得PE=BE,∴PE=2AE,
∴∠APE=30°,∴∠AEP=90°-30°=60°,
∴∠BEF=(180°-∠AEP)=×(180°-60°)=60°,
∴∠EFB=90°-60°=30°,
∴EF=2BE,故①正确;
∵BE=PE,∴EF=2PE.
∵EF>PF,
∴PF<2PE,故②错误;
由翻折的性质,得EF⊥PB,
∴∠EBQ=∠EFB=30°,
∴BE=2EQ,EF=2BE,
∴FQ=3EQ,故③错误;
由翻折的性质,得∠EFB=∠EFP=30°,
且BF=PF,
∴∠BFP=30°+30°=60°,
∴△PBF是等边三角形,故④正确.
综上所述,正确的结论是①④.故选D.
12.解:(1)证明:由折叠的性质,得PE=BE,
∴∠EBP=∠EPB.
由题易知∠EPH=∠EBC=90°,
∴∠EPH-∠EPB=∠EBC-∠EBP,
即∠PBC=∠BPH.
由题易知AD∥BC,
∴∠APB=∠PBC,∴∠APB=∠BPH.
(2)△PDH的周长不变,为定值8.
证明:过点B作BQ⊥PH,垂足为Q.
由(1)知∠APB=∠BPH.
在△ABP和△QBP中,
∴△ABP≌△QBP(AAS),
∴AP=QP,AB=QB.
由题易知AB=BC,
∴BC=QB.
又由题易知∠C=∠BQH=90°,
∴△BCH和△BQH均为直角三角形.
又∵BH=BH,
∴Rt△BCH≌Rt△BQH,
∴CH=QH,
故△PDH的周长为PD+DH+PH=AP+PD+DH+HC=AD+CD=8.
13.解:(1)证明:由折叠的性质,得AD=DE,∠BCO=∠DCO=∠ADO=∠CDO=45°,
∴BC=DE,∠COD=90°,OC=OD.
在△OBC和△OED中,
∴△OBC≌△OED(SAS).
(2)如图,过点O作OH⊥CD于点H.
由(1)得△OBC≌△OED,∴OE=OB.
∵BC=x,∴AD=DE=x,
∴CE=8-x.
∵OC=OD,∠COD=90°,
∴CH=CD=AB=×8=4,OH=
CD=4,
∴EH=CH-CE=4-(8-x)=x-4.
在Rt△OHE中,由勾股定理得OE2=OH2+EH2,
即OB2=42+(x-4)2,
∴y关于x的关系式为y=x2-8x+32.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
