2020--2021学年八年级数学下册同步课时练习:第一章 直角三角形 单元测试(word版含答案)
文档属性
| 名称 | 2020--2021学年八年级数学下册同步课时练习:第一章 直角三角形 单元测试(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 168.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 15:30:22 | ||
图片预览

文档简介
第1章 直角三角形
单元测试
一、选择题(每小题3分,共24分)
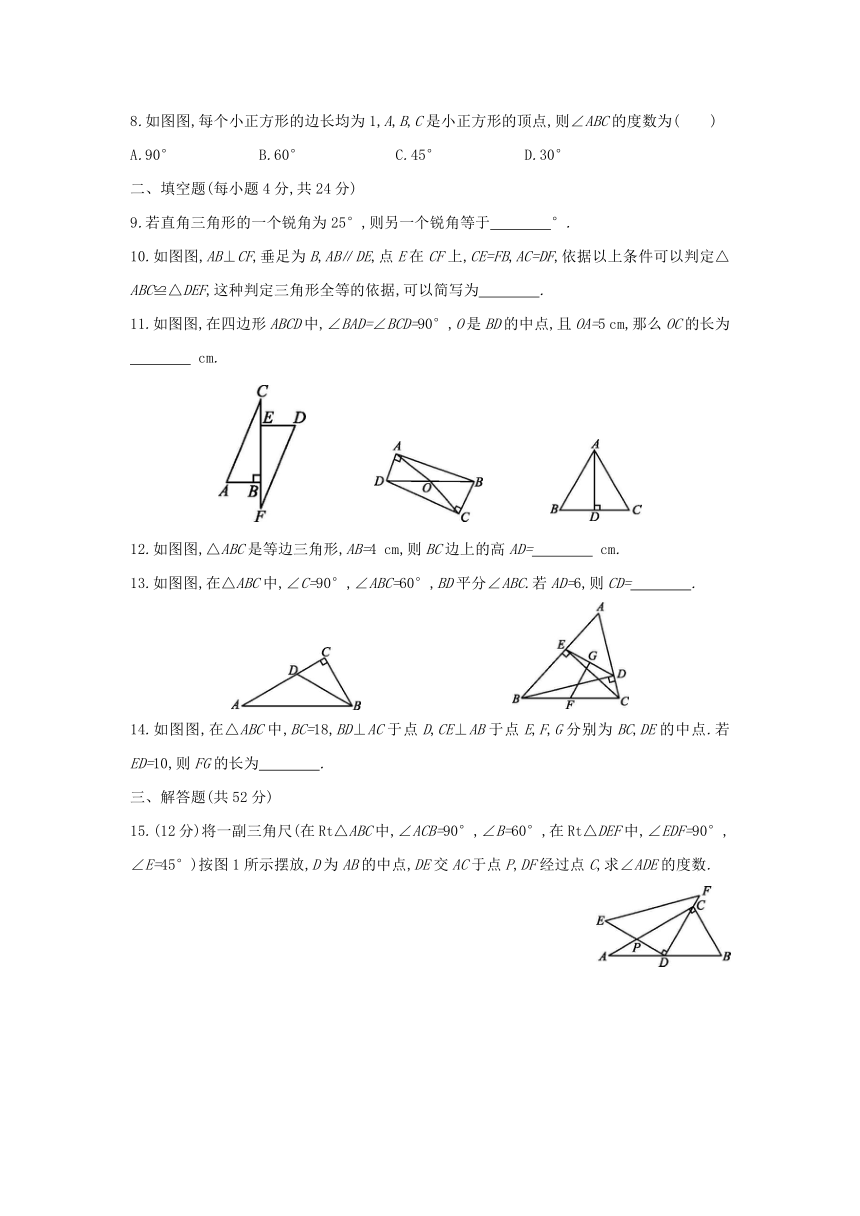
1.如图图,在△ABC中,∠C=90°,则∠B的度数为
( )
A.15°
B.30°
C.50°
D.60°
2.在Rt△ABC中,∠C=90°,其中的一个锐角为30°,最短边的长为5
cm,则最长边上的中线长为
( )
A.5
cm
B.15
cm
C.10
cm
D.2.5
cm
3.以下列长度的线段为边,不能构成直角三角形的是
( )
A.8,15,17
B.11,60,61
C.2,3,4
D.7,24,25
4.若△ABC的三边长分别为a,b,c,且(a+b)(a-b)=c2,则△ABC是
( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.无法判断
5.如图图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件
( )
A.∠BAC=∠BAD
B.AC=AD或BC=BD
C.AC=AD且BC=BD
D.以上都不正确
6.如图图,AB⊥AC于点A,BD⊥CD于点D,若AC=DB,则下列结论中不正确的是
( )
A.∠A=∠D
B.∠ABC=∠DCB
C.OB=OD
D.OA=OD
7.如图图,直线AB,CD相交于点O,PE⊥CD于点E,PF⊥AB于点F.若PE=PF,∠AOC=50°,则∠AOP的度数为
( )
A.65°
B.60°
C.40°
D.30°
8.如图图,每个小正方形的边长均为1,A,B,C是小正方形的顶点,则∠ABC的度数为( )
A.90°
B.60°
C.45°
D.30°
二、填空题(每小题4分,共24分)
9.若直角三角形的一个锐角为25°,则另一个锐角等于 °.?
10.如图图,AB⊥CF,垂足为B,AB∥DE,点E在CF上,CE=FB,AC=DF,依据以上条件可以判定△ABC≌△DEF,这种判定三角形全等的依据,可以简写为 .?
11.如图图,在四边形ABCD中,∠BAD=∠BCD=90°,O是BD的中点,且OA=5
cm,那么OC的长为
cm.?
12.如图图,△ABC是等边三角形,AB=4
cm,则BC边上的高AD=
cm.?
13.如图图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC.若AD=6,则CD= .?
14.如图图,在△ABC中,BC=18,BD⊥AC于点D,CE⊥AB于点E,F,G分别为BC,DE的中点.若ED=10,则FG的长为 .?
三、解答题(共52分)
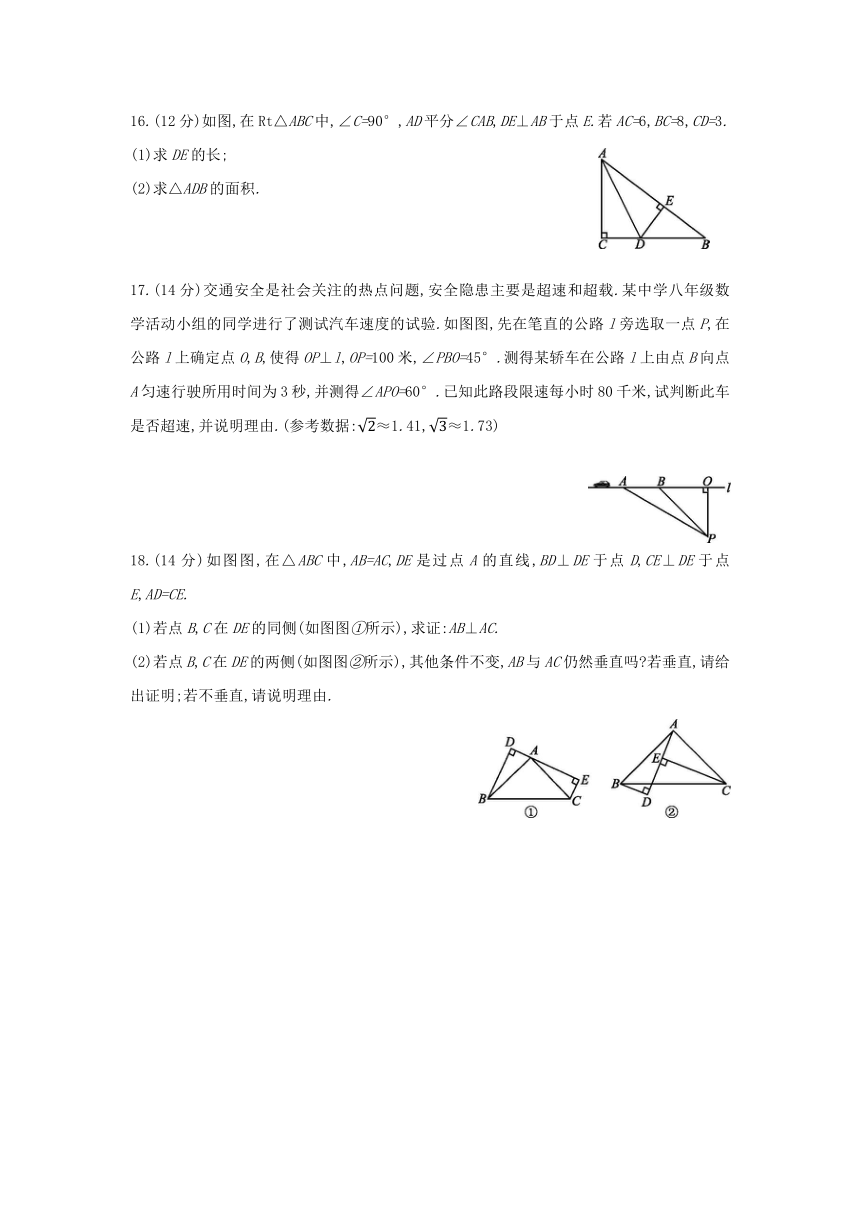
15.(12分)将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△DEF中,∠EDF=90°,∠E=45°)按图1所示摆放,D为AB的中点,DE交AC于点P,DF经过点C,求∠ADE的度数.
16.(12分)如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E.若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.
17.(14分)交通安全是社会关注的热点问题,安全隐患主要是超速和超载.某中学八年级数学活动小组的同学进行了测试汽车速度的试验.如图图,先在笔直的公路l旁选取一点P,在公路l上确定点O,B,使得OP⊥l,OP=100米,∠PBO=45°.测得某轿车在公路l上由点B向点A匀速行驶所用时间为3秒,并测得∠APO=60°.已知此路段限速每小时80千米,试判断此车是否超速,并说明理由.(参考数据:≈1.41,≈1.73)
18.(14分)如图图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E,AD=CE.
(1)若点B,C在DE的同侧(如图图①所示),求证:AB⊥AC.
(2)若点B,C在DE的两侧(如图图②所示),其他条件不变,AB与AC仍然垂直吗?若垂直,请给出证明;若不垂直,请说明理由.
1.D
2.A
3.C
4.A
5.B
6.C
7.A
8.C
连接AC.根据题意,得AC=BC=,AB=.
∵()2+()2=()2,∴AC2+BC2=AB2,∴△ABC是等腰直角三角形,
∴∠ABC=45°.
9.65
10.HL
∵AB⊥CF,AB∥DE,∴DE⊥CF,∴△ABC和△DEF都是直角三角形.∵CE=FB,∴CB=FE.又∵AC=DF,∴由HL定理可判定Rt△ABC≌Rt△DEF.
11.5
12.2
13.3
由∠C=90°,∠ABC=60°,BD平分∠ABC,可知∠A=30°,∠ABD=∠DBC=30°,所以∠A=∠ABD,所以AD=BD=6.在Rt△BDC中,∠DBC=30°,BD=6,所以CD=3.
14.2
如图图,连接EF,DF.
∵BD⊥AC,CE⊥AB,F是BC的中点,
∴在Rt△CEB中,EF=BC.
在Rt△BDC中,DF=BC,
∴EF=DF=9,
∴△EFD为等腰三角形.
又∵G是DE的中点,
∴FG是等腰三角形EFD的中线,
∴FG⊥DE,EG=DG=5.
在Rt△GDF中,FG===2.
15.解:∵∠ACB=90°,D为AB的中点,∠B=60°,
∴CD=AD=BD=AB,∠A=30°,
∴∠ACD=∠A=30°,
∴∠ADC=180°-30°×2=120°,
∴∠ADE=∠ADC-∠EDF=120°-90°=30°.
16.解:(1)∵在Rt△ABC中,∠C=90°,
∴AC⊥CD.
又∵AD平分∠CAB,DE⊥AB,∴DE=CD.
∵CD=3,∴DE=3.
(2)在Rt△ABC中,∠C=90°,AC=6,BC=8,
∴AB===10,
∴S△ADB=AB·DE=×10×3=15.
17.解:此车超速.
理由:∵∠POB=90°,∠PBO=45°,
∴△POB是等腰直角三角形,
∴OB=OP=100米.
∵∠APO=60°,
∴∠OAP=30°,
∴AP=2OP=200米,
∴OA=≈173(米),
∴AB=OA-OB≈73(米).
73÷3≈24(米/秒)≈86千米/时>80千米/时,
∴此车超速.
18.解:(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠CEA=90°.
在Rt△ABD和Rt△CAE中,
∵AB=CA,AD=CE,
∴Rt△ABD≌Rt△CAE,
∴∠DAB=∠ECA.
∵∠EAC+∠ECA=90°,
∴∠EAC+∠DAB=90°,
∴∠BAC=180°-(∠EAC+∠DAB)=90°,
∴AB⊥AC.
(2)AB与AC仍然垂直.
证明:同(1)可得Rt△ABD≌Rt△CAE,
∴∠DAB=∠ECA.
∵∠EAC+∠ECA=90°,
∴∠EAC+∠DAB=90°,即∠BAC=90°,
∴AB⊥AC.
单元测试
一、选择题(每小题3分,共24分)
1.如图图,在△ABC中,∠C=90°,则∠B的度数为
( )
A.15°
B.30°
C.50°
D.60°
2.在Rt△ABC中,∠C=90°,其中的一个锐角为30°,最短边的长为5
cm,则最长边上的中线长为
( )
A.5
cm
B.15
cm
C.10
cm
D.2.5
cm
3.以下列长度的线段为边,不能构成直角三角形的是
( )
A.8,15,17
B.11,60,61
C.2,3,4
D.7,24,25
4.若△ABC的三边长分别为a,b,c,且(a+b)(a-b)=c2,则△ABC是
( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.无法判断
5.如图图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件
( )
A.∠BAC=∠BAD
B.AC=AD或BC=BD
C.AC=AD且BC=BD
D.以上都不正确
6.如图图,AB⊥AC于点A,BD⊥CD于点D,若AC=DB,则下列结论中不正确的是
( )
A.∠A=∠D
B.∠ABC=∠DCB
C.OB=OD
D.OA=OD
7.如图图,直线AB,CD相交于点O,PE⊥CD于点E,PF⊥AB于点F.若PE=PF,∠AOC=50°,则∠AOP的度数为
( )
A.65°
B.60°
C.40°
D.30°
8.如图图,每个小正方形的边长均为1,A,B,C是小正方形的顶点,则∠ABC的度数为( )
A.90°
B.60°
C.45°
D.30°
二、填空题(每小题4分,共24分)
9.若直角三角形的一个锐角为25°,则另一个锐角等于 °.?
10.如图图,AB⊥CF,垂足为B,AB∥DE,点E在CF上,CE=FB,AC=DF,依据以上条件可以判定△ABC≌△DEF,这种判定三角形全等的依据,可以简写为 .?
11.如图图,在四边形ABCD中,∠BAD=∠BCD=90°,O是BD的中点,且OA=5
cm,那么OC的长为
cm.?
12.如图图,△ABC是等边三角形,AB=4
cm,则BC边上的高AD=
cm.?
13.如图图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC.若AD=6,则CD= .?
14.如图图,在△ABC中,BC=18,BD⊥AC于点D,CE⊥AB于点E,F,G分别为BC,DE的中点.若ED=10,则FG的长为 .?
三、解答题(共52分)
15.(12分)将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△DEF中,∠EDF=90°,∠E=45°)按图1所示摆放,D为AB的中点,DE交AC于点P,DF经过点C,求∠ADE的度数.
16.(12分)如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E.若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.
17.(14分)交通安全是社会关注的热点问题,安全隐患主要是超速和超载.某中学八年级数学活动小组的同学进行了测试汽车速度的试验.如图图,先在笔直的公路l旁选取一点P,在公路l上确定点O,B,使得OP⊥l,OP=100米,∠PBO=45°.测得某轿车在公路l上由点B向点A匀速行驶所用时间为3秒,并测得∠APO=60°.已知此路段限速每小时80千米,试判断此车是否超速,并说明理由.(参考数据:≈1.41,≈1.73)
18.(14分)如图图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E,AD=CE.
(1)若点B,C在DE的同侧(如图图①所示),求证:AB⊥AC.
(2)若点B,C在DE的两侧(如图图②所示),其他条件不变,AB与AC仍然垂直吗?若垂直,请给出证明;若不垂直,请说明理由.
1.D
2.A
3.C
4.A
5.B
6.C
7.A
8.C
连接AC.根据题意,得AC=BC=,AB=.
∵()2+()2=()2,∴AC2+BC2=AB2,∴△ABC是等腰直角三角形,
∴∠ABC=45°.
9.65
10.HL
∵AB⊥CF,AB∥DE,∴DE⊥CF,∴△ABC和△DEF都是直角三角形.∵CE=FB,∴CB=FE.又∵AC=DF,∴由HL定理可判定Rt△ABC≌Rt△DEF.
11.5
12.2
13.3
由∠C=90°,∠ABC=60°,BD平分∠ABC,可知∠A=30°,∠ABD=∠DBC=30°,所以∠A=∠ABD,所以AD=BD=6.在Rt△BDC中,∠DBC=30°,BD=6,所以CD=3.
14.2
如图图,连接EF,DF.
∵BD⊥AC,CE⊥AB,F是BC的中点,
∴在Rt△CEB中,EF=BC.
在Rt△BDC中,DF=BC,
∴EF=DF=9,
∴△EFD为等腰三角形.
又∵G是DE的中点,
∴FG是等腰三角形EFD的中线,
∴FG⊥DE,EG=DG=5.
在Rt△GDF中,FG===2.
15.解:∵∠ACB=90°,D为AB的中点,∠B=60°,
∴CD=AD=BD=AB,∠A=30°,
∴∠ACD=∠A=30°,
∴∠ADC=180°-30°×2=120°,
∴∠ADE=∠ADC-∠EDF=120°-90°=30°.
16.解:(1)∵在Rt△ABC中,∠C=90°,
∴AC⊥CD.
又∵AD平分∠CAB,DE⊥AB,∴DE=CD.
∵CD=3,∴DE=3.
(2)在Rt△ABC中,∠C=90°,AC=6,BC=8,
∴AB===10,
∴S△ADB=AB·DE=×10×3=15.
17.解:此车超速.
理由:∵∠POB=90°,∠PBO=45°,
∴△POB是等腰直角三角形,
∴OB=OP=100米.
∵∠APO=60°,
∴∠OAP=30°,
∴AP=2OP=200米,
∴OA=≈173(米),
∴AB=OA-OB≈73(米).
73÷3≈24(米/秒)≈86千米/时>80千米/时,
∴此车超速.
18.解:(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠CEA=90°.
在Rt△ABD和Rt△CAE中,
∵AB=CA,AD=CE,
∴Rt△ABD≌Rt△CAE,
∴∠DAB=∠ECA.
∵∠EAC+∠ECA=90°,
∴∠EAC+∠DAB=90°,
∴∠BAC=180°-(∠EAC+∠DAB)=90°,
∴AB⊥AC.
(2)AB与AC仍然垂直.
证明:同(1)可得Rt△ABD≌Rt△CAE,
∴∠DAB=∠ECA.
∵∠EAC+∠ECA=90°,
∴∠EAC+∠DAB=90°,即∠BAC=90°,
∴AB⊥AC.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
