2020-2021学年北师大版八年级下册数学 5.3分式的加减 同步练习(word版,含答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级下册数学 5.3分式的加减 同步练习(word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 178.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 05:51:30 | ||
图片预览



文档简介
5.3分式的加减 同步练习
一.选择题
1.计算的结果是( )
A.5 B.﹣5 C. D.
2.计算﹣的结果为( )
A.1 B.3 C. D.
3.计算﹣÷的结果为( )
A.0 B. C. D.
4.计算+的结果为( )
A.1 B. C. D.
5.化简的结果是( )
A. B. C. D.
6.在化简分式的过程中,开始出现错误的步骤是( )
A.A B.B C.C D.D
7.在化简分式+的过程中,开始出现错误的步骤是( )
A.﹣
B.
C.
D.
8.下列分式化简正确的是( )
A.
B.
C.
D.
9.已知实数x,y,z满足++=,且=11,则x+y+z的值为( )
A.12 B.14 C. D.9
10.已知a,b为实数且满足a≠﹣1,b≠﹣1,设M=+,N=+.
①若ab=1时,M=N
②若ab>1时,M>N
③若ab<1时,M<N
④若a+b=0,则M?N≤0
则上述四个结论正确的有( )个.
A.1 B.2 C.3 D.4
二.填空题
11.计算:(﹣)?= .
12.计算:﹣= .
13.计算:= .
14.化简:(﹣1)÷= .
15.计算﹣的结果是 .
三.解答题
16.化简:(﹣a+1)÷.
17.观察如图所示的小明的作业,回答下列问题.
小明的作业
解:(﹣1)÷﹣
=?﹣ 第一步
=﹣﹣ 第二步
=﹣2a+b. 第三步
(1)小明的作业中,从第 步开始出现错误.
(2)从第二步到第三步是否正确?若不正确,请说明错误原因.
(3)请写出正确的计算过程.
18.仿照例子,将分式拆分成一个整式与一个分式的和(差)的形式.
示例:.
解:.
请仿照示例,拆分分式.
参考答案
一.选择题
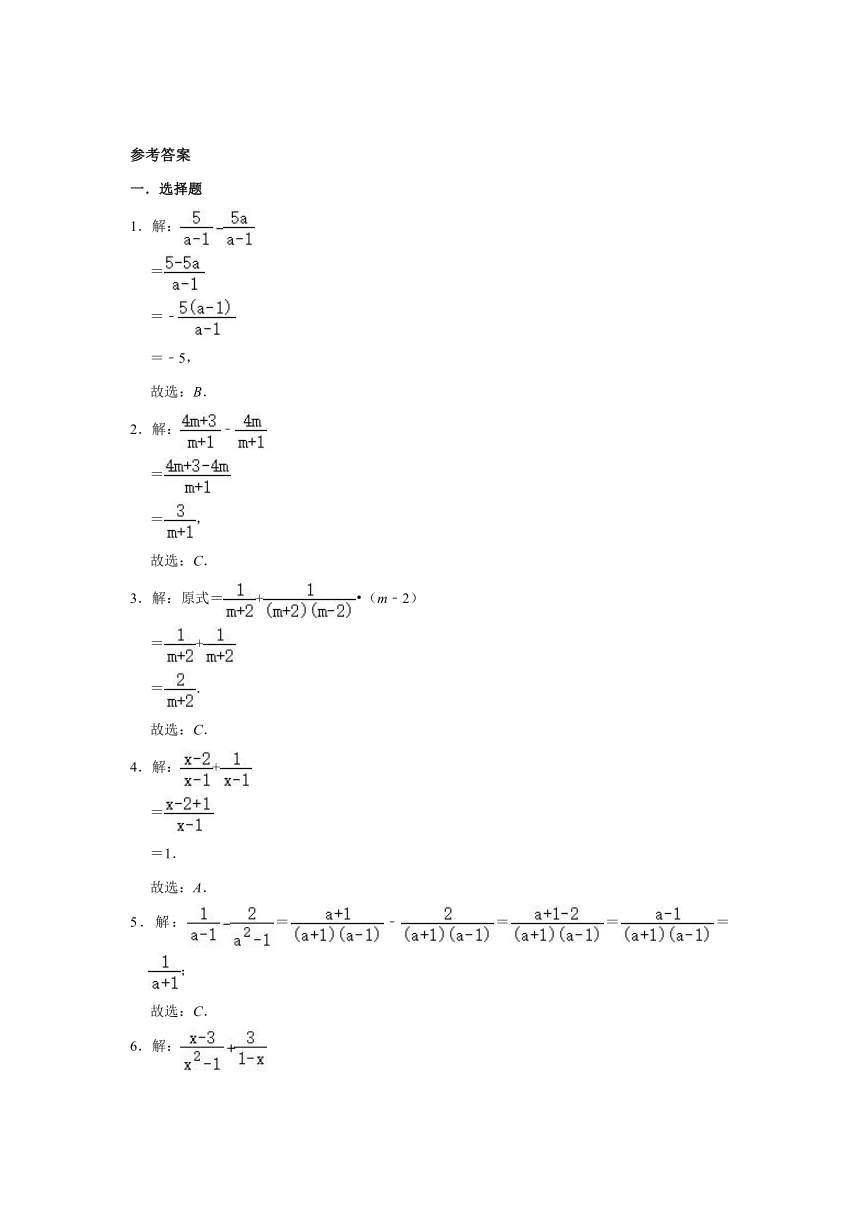
1.解:
=
=﹣
=﹣5,
故选:B.
2.解:﹣
=
=,
故选:C.
3.解:原式=+?(m﹣2)
=+
=.
故选:C.
4.解:+
=
=1.
故选:A.
5.解:=﹣===;
故选:C.
6.解:
=﹣
=
即从B开始出错.
故选:B.
7.解:∵正确的解题步骤是:
原式=﹣
=﹣
=
=
=﹣,
∴开始出现错误的步骤是选项B.
故选:B.
8.解:A、=2(a+b)=2a+2b,故原题计算错误;
B、==,故原题计算正确;
C、==,故原题计算错误;
D、不能约分,故原题计算错误;
故选:B.
9.解:∵=11,
∴1++1++1+=14,
即++=14,
∴++=,
而++=,
∴=,
∴x+y+z=12.
故选:A.
10.解:∵M=+,N=+,
∴M﹣N=+﹣(+)=+==,
①当ab=1时,M﹣N=0,
∴M=N,故①正确;
②当ab>1时,2ab>2,
∴2ab﹣2>0,
当a<0时,b<0,(a+1)(b+1)>0或(a+1)(b+1)<0,
∴M﹣N>0或M﹣N<0,
∴M>N或M<N,故②错误;
③当ab<1时,a和b可能同号,也可能异号,
∴(a+1)(b+1)>0或(a+1)(b+1)<0,而2ab﹣2<0,
∴M>N或M<N,故③错误;
④M?N=(+)?(+)
=++,
∵a+b=0,
∴原式=+==,
∵a≠﹣1,b≠﹣1,
∴(a+1)2(b+1)2>0,
∵a+b=0
∴ab≤0,M?N≤0,故④正确.
故选:B.
二.填空题
11.解:原式=?(x+1)
=(x+1)2
=x2+2x+1,
故答案为:x2+2x+1.
12.解:原式=
=
=.
故答案为:.
13.解:原式=+
=+
=+
=
=.
故答案为:.
14.解:(﹣1)÷
=
=
=,
故答案为:.
15.解:原式=﹣
=﹣
=.
故答案为:.
三.解答题
16.解:原式=(﹣)×
=×
=×
=.
17.解:(1)小明的作业中,从第一步开始出现错误;
故答案为:(1)一;
(2)从第二步到第三步不正确,错误原因是没有分母(a+b)了;
(3)原式=?﹣
=?﹣
=﹣
=﹣.
18.解:原式=
=2x2+3﹣.
一.选择题
1.计算的结果是( )
A.5 B.﹣5 C. D.
2.计算﹣的结果为( )
A.1 B.3 C. D.
3.计算﹣÷的结果为( )
A.0 B. C. D.
4.计算+的结果为( )
A.1 B. C. D.
5.化简的结果是( )
A. B. C. D.
6.在化简分式的过程中,开始出现错误的步骤是( )
A.A B.B C.C D.D
7.在化简分式+的过程中,开始出现错误的步骤是( )
A.﹣
B.
C.
D.
8.下列分式化简正确的是( )
A.
B.
C.
D.
9.已知实数x,y,z满足++=,且=11,则x+y+z的值为( )
A.12 B.14 C. D.9
10.已知a,b为实数且满足a≠﹣1,b≠﹣1,设M=+,N=+.
①若ab=1时,M=N
②若ab>1时,M>N
③若ab<1时,M<N
④若a+b=0,则M?N≤0
则上述四个结论正确的有( )个.
A.1 B.2 C.3 D.4
二.填空题
11.计算:(﹣)?= .
12.计算:﹣= .
13.计算:= .
14.化简:(﹣1)÷= .
15.计算﹣的结果是 .
三.解答题
16.化简:(﹣a+1)÷.
17.观察如图所示的小明的作业,回答下列问题.
小明的作业
解:(﹣1)÷﹣
=?﹣ 第一步
=﹣﹣ 第二步
=﹣2a+b. 第三步
(1)小明的作业中,从第 步开始出现错误.
(2)从第二步到第三步是否正确?若不正确,请说明错误原因.
(3)请写出正确的计算过程.
18.仿照例子,将分式拆分成一个整式与一个分式的和(差)的形式.
示例:.
解:.
请仿照示例,拆分分式.
参考答案
一.选择题
1.解:
=
=﹣
=﹣5,
故选:B.
2.解:﹣
=
=,
故选:C.
3.解:原式=+?(m﹣2)
=+
=.
故选:C.
4.解:+
=
=1.
故选:A.
5.解:=﹣===;
故选:C.
6.解:
=﹣
=
即从B开始出错.
故选:B.
7.解:∵正确的解题步骤是:
原式=﹣
=﹣
=
=
=﹣,
∴开始出现错误的步骤是选项B.
故选:B.
8.解:A、=2(a+b)=2a+2b,故原题计算错误;
B、==,故原题计算正确;
C、==,故原题计算错误;
D、不能约分,故原题计算错误;
故选:B.
9.解:∵=11,
∴1++1++1+=14,
即++=14,
∴++=,
而++=,
∴=,
∴x+y+z=12.
故选:A.
10.解:∵M=+,N=+,
∴M﹣N=+﹣(+)=+==,
①当ab=1时,M﹣N=0,
∴M=N,故①正确;
②当ab>1时,2ab>2,
∴2ab﹣2>0,
当a<0时,b<0,(a+1)(b+1)>0或(a+1)(b+1)<0,
∴M﹣N>0或M﹣N<0,
∴M>N或M<N,故②错误;
③当ab<1时,a和b可能同号,也可能异号,
∴(a+1)(b+1)>0或(a+1)(b+1)<0,而2ab﹣2<0,
∴M>N或M<N,故③错误;
④M?N=(+)?(+)
=++,
∵a+b=0,
∴原式=+==,
∵a≠﹣1,b≠﹣1,
∴(a+1)2(b+1)2>0,
∵a+b=0
∴ab≤0,M?N≤0,故④正确.
故选:B.
二.填空题
11.解:原式=?(x+1)
=(x+1)2
=x2+2x+1,
故答案为:x2+2x+1.
12.解:原式=
=
=.
故答案为:.
13.解:原式=+
=+
=+
=
=.
故答案为:.
14.解:(﹣1)÷
=
=
=,
故答案为:.
15.解:原式=﹣
=﹣
=.
故答案为:.
三.解答题
16.解:原式=(﹣)×
=×
=×
=.
17.解:(1)小明的作业中,从第一步开始出现错误;
故答案为:(1)一;
(2)从第二步到第三步不正确,错误原因是没有分母(a+b)了;
(3)原式=?﹣
=?﹣
=﹣
=﹣.
18.解:原式=
=2x2+3﹣.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
