2020-2021学年青岛 版九年级下册数学《第7章 空间图形的初步认识》单元测试卷(word版,含答案)
文档属性
| 名称 | 2020-2021学年青岛 版九年级下册数学《第7章 空间图形的初步认识》单元测试卷(word版,含答案) |  | |
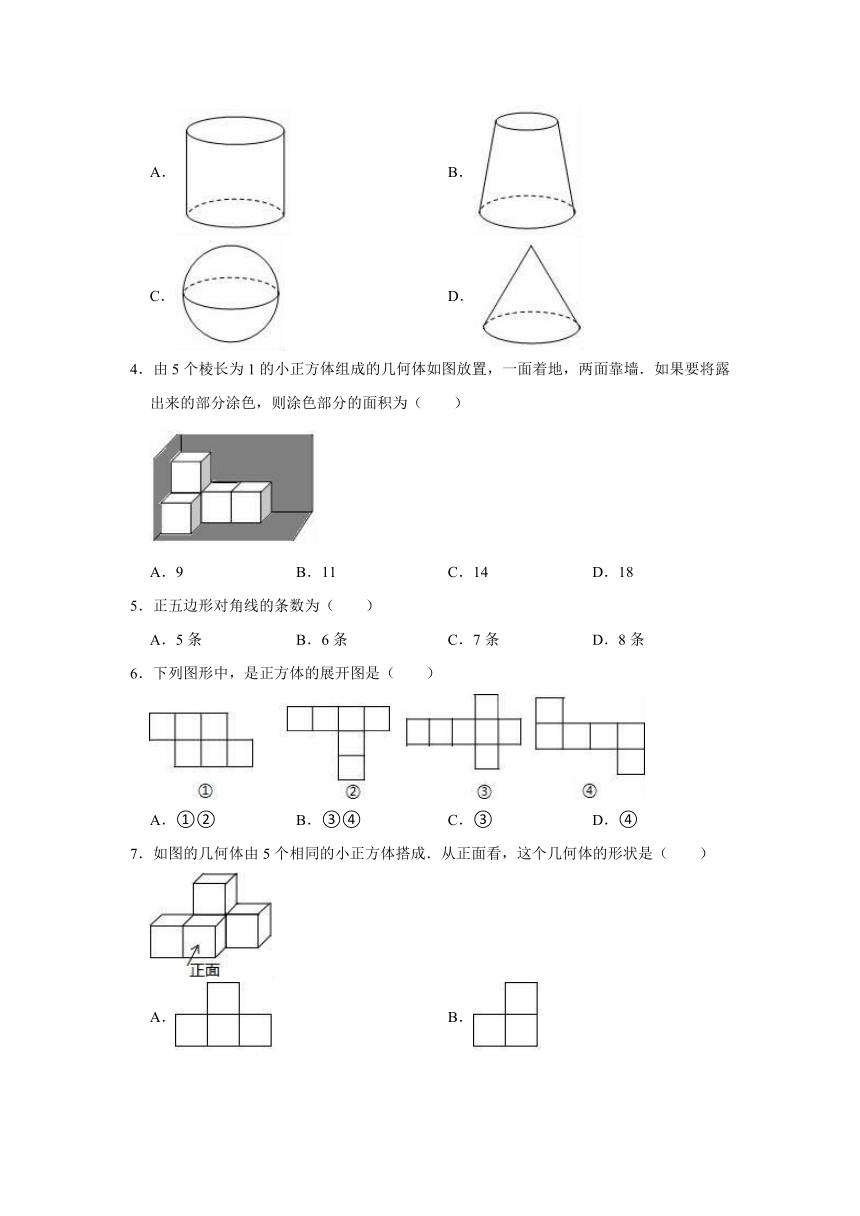
| 格式 | doc | ||
| 文件大小 | 171.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 05:50:21 | ||
图片预览


文档简介
2020-2021学年青岛新版九年级下册数学《第7章 空间图形的初步认识》单元测试卷
一.选择题
1.下列第一行所示的四个图形,每个图形均是由四种简单的图形a、b、c、d(圆、直线、三角形、长方形)中的两种组成.例如由a、b组成的图形记作a⊙b,那么由此可知,下列第二行的图中可以记作a⊙d的是( )
A. B.
C. D.
2.将下左图直角三角形ABC绕直角边AC旋转一周,所得几何体从正面是( )
A. B. C. D.
3.将如图所示的平面图形绕轴旋转一周,可以得到的立体图形是( )
A. B.
C. D.
4.由5个棱长为1的小正方体组成的几何体如图放置,一面着地,两面靠墙.如果要将露出来的部分涂色,则涂色部分的面积为( )
A.9 B.11 C.14 D.18
5.正五边形对角线的条数为( )
A.5条 B.6条 C.7条 D.8条
6.下列图形中,是正方体的展开图是( )
A.①② B.③④ C.③ D.④
7.如图的几何体由5个相同的小正方体搭成.从正面看,这个几何体的形状是( )
A. B.
C. D.
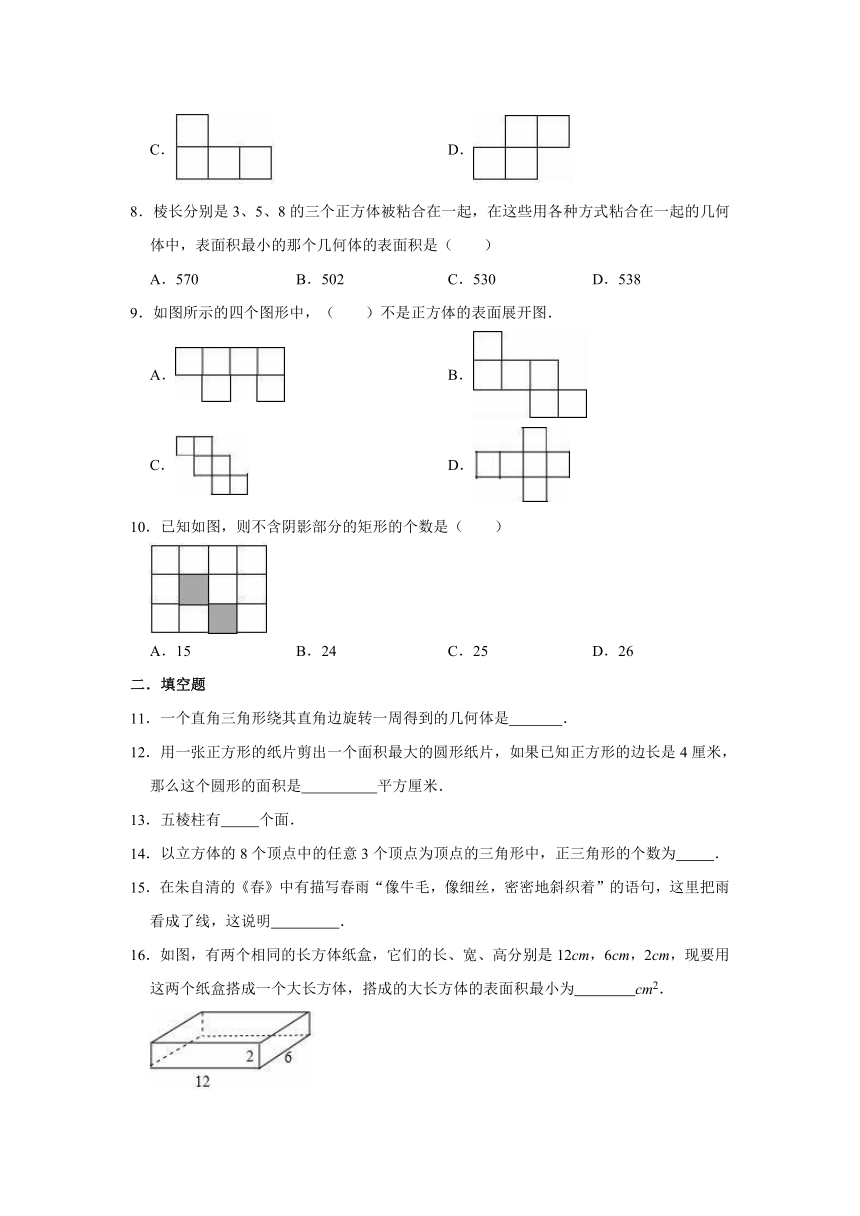
8.棱长分别是3、5、8的三个正方体被粘合在一起,在这些用各种方式粘合在一起的几何体中,表面积最小的那个几何体的表面积是( )
A.570 B.502 C.530 D.538
9.如图所示的四个图形中,( )不是正方体的表面展开图.
A. B.
C. D.
10.已知如图,则不含阴影部分的矩形的个数是( )
A.15 B.24 C.25 D.26
二.填空题
11.一个直角三角形绕其直角边旋转一周得到的几何体是 .
12.用一张正方形的纸片剪出一个面积最大的圆形纸片,如果已知正方形的边长是4厘米,那么这个圆形的面积是 平方厘米.
13.五棱柱有 个面.
14.以立方体的8个顶点中的任意3个顶点为顶点的三角形中,正三角形的个数为 .
15.在朱自清的《春》中有描写春雨“像牛毛,像细丝,密密地斜织着”的语句,这里把雨看成了线,这说明 .
16.如图,有两个相同的长方体纸盒,它们的长、宽、高分别是12cm,6cm,2cm,现要用这两个纸盒搭成一个大长方体,搭成的大长方体的表面积最小为 cm2.
17.如图,5个边长为1cm的正方体摆在桌子上,则露在表面的部分的面积为 cm2.
18.一个圆被分成四个扇形,若各个扇形的面积之比为4:2:1:3,则最小的扇形的圆心角的度数为 .
19.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是 .
20.一个无盖的长方形包装盒展开后如图所示(单位:cm),则其容积为 cm3.
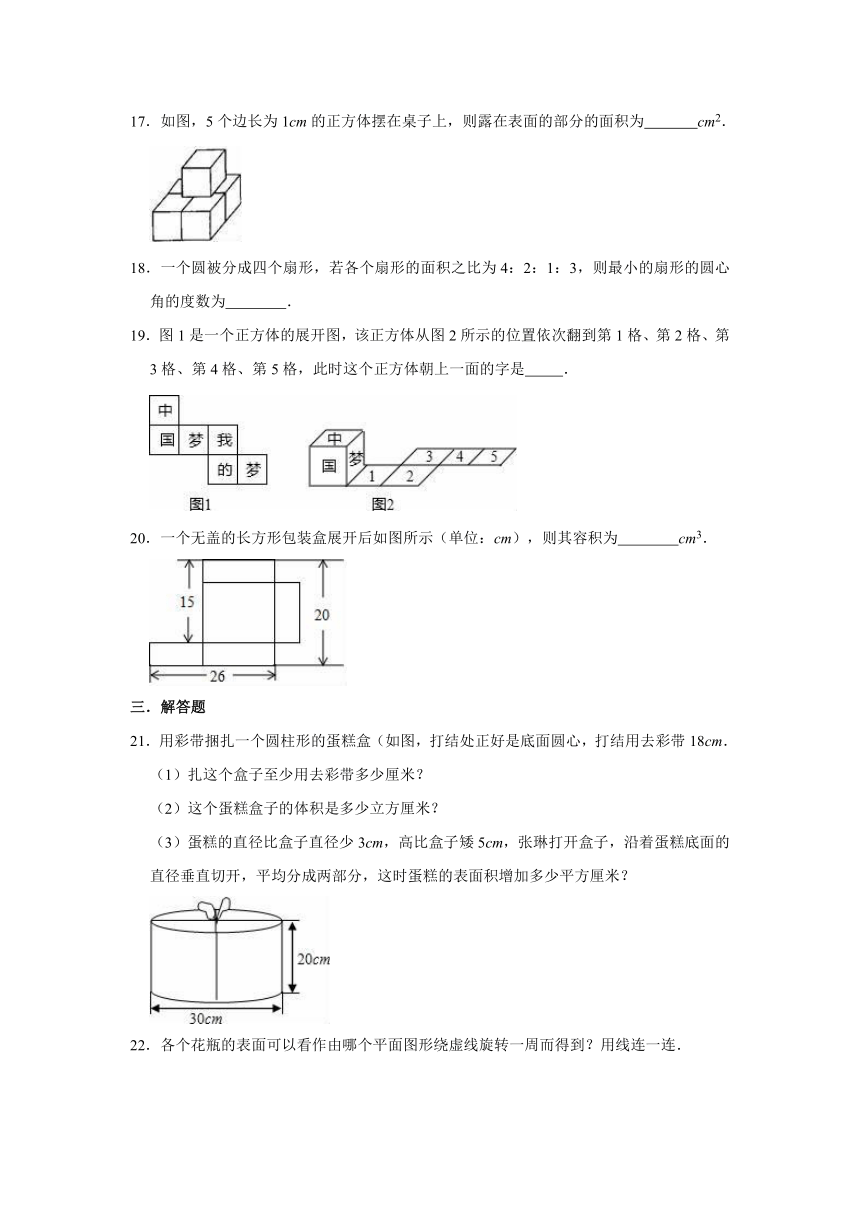
三.解答题
21.用彩带捆扎一个圆柱形的蛋糕盒(如图,打结处正好是底面圆心,打结用去彩带18cm.
(1)扎这个盒子至少用去彩带多少厘米?
(2)这个蛋糕盒子的体积是多少立方厘米?
(3)蛋糕的直径比盒子直径少3cm,高比盒子矮5cm,张琳打开盒子,沿着蛋糕底面的直径垂直切开,平均分成两部分,这时蛋糕的表面积增加多少平方厘米?
22.各个花瓶的表面可以看作由哪个平面图形绕虚线旋转一周而得到?用线连一连.
23.如图所示的几何体是由若干个相同的小正方体搭建而成的(第一层,1个;第二层3个;第3层,6个),小正方体的一个侧面的面积为1.今要用红颜色给这个几何体的表面着色(但底部不着色),要着色的面积是多少?
24.在把如图折叠成正方体后,
(1)AB与GB的位置关系是 ;
(2)CB与GB的位置关系是 ;
(3)AB与BC的位置关系是 ,理由解释为 .
25.如图所示,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成一正方体的表面展开图.(填出两种答案)
26.在一个长方形中,长和宽分别为4cm、3cm,若该长方形绕着它的一边旋转一周,形成的几何体的体积是多少?(结果用π表示)
27.如图是一个正方体纸盒的展开图,请把﹣10,7,10,﹣2,﹣7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数.
参考答案与试题解析
一.选择题
1.解:根据题意,知a代表长方形,d代表直线,所以记作a⊙d的图形是长方形和直线的组合,
故选:A.
2.解:直角三角形ABC绕直角边AC旋转一周可得圆锥,从正面看图形是等腰三角形.
故选:D.
3.解:绕直线l旋转一周,可以得到圆台,
故选:B.
4.解:由图可知涂色部分是从上、前、右三个方向所涂面积相加,即涂色部分面积为4+4+3=11,
故选:B.
5.解:由题意得:5(5﹣3)÷2=5,
故选:A.
6.解:①中间4个正方形是“田字形”,不是正方体展开图;
②折叠后有两个正方形重合,不是正方体展开图;
③不符合正方体展开图;
④符合正方体展开图;
故,是正方体展开图的是④.
故选:D.
7.解:从正面看第一层是三个小正方形,第二层中间一个小正方形,
故选:A.
8.解:(3×3+5×5+8×8)×6﹣(3×3)×4﹣(5×5)×2
=98×6﹣9×4﹣25×2
=588﹣36﹣50
=502.
故选:B.
9.解:A、折叠后第二行两个面无法折起来,不能折成正方体;B、C、D都是正方体的展开图.
故选:A.
10.解:根据以上分析不含阴影的矩形个数为26个.
故选:D.
二.填空题
11.解:以直角三角形的一条直角边所在直线为对称轴旋转一周,得到一个圆锥,
故答案为:圆锥.
12.解:∵正方形的边长是4厘米,
∴剪出的最大的圆直径为4厘米,
半径=2厘米,
所以,圆的面积=πr2=3.14×22=12.56(平方厘米).
故答案为:12.56.
13.解:∵五棱柱有2个底面,5个侧面,
∴五棱柱的面数为7.
故答案为:7.
14.解:如图所示:
正三角形的各边必为立方体各面的对角线,有△ADF,△ADH,△AFH,△BCE,△BCG,△BEG,△CEG,△DFH共8个正三角形.
故答案为:8.
15.解:“像牛毛,像细丝,密密地斜织着”的语句,这里把雨看成了线,这说明点动成线.
故答案为:点动成线.
16.解:(1)图1中,长方体的高为4,表面积=2(12×6+12×4+4×6)=288cm2.
图2中,长为24,表面积=2(24×6+24×2+6×2)=408cm2.
图3中,宽为12,表面积=2(12×12+12×2+12×2)=384cm2.
∴图1的表面积最小.
故答案为:288.
17.解:根据以上分析故露在表面的部分的面积为16cm2.故
答案为16.
18.解:∵扇形A,B,C,D的面积之比为4:2:1:3,
∴其所占扇形比分别为:,
∴最小的扇形的圆心角是360°×=36°.
故答案为:36°.
19.解:由图1可得,“中”和“的”相对;“国”和“我”相对;“梦”和“梦”相对;
由图2可得,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格时,“国”在下面,则这时小正方体朝上一面的字是“我”.
故答案为:我.
20.解:20﹣15=5(cm),
15﹣5=10(cm),
26﹣10=16(cm),
16×10×5=800(cm3).
答:其容积为800cm3.
故答案为:800.
三.解答题
21.解:(1)2(30×2+20×2)+18=218cm,
答:扎这个盒子至少用去彩带218cm;
(2)由圆柱的体积,得
3.14×()2×20=14130(cm3),
答:这个蛋糕盒子的体积是14130cm3
(3)蛋糕的直径是30﹣3=27cm,蛋糕的高是20﹣5=15cm,
截面的面积是27×15×2=810cm2.
答:蛋糕的表面积增加810平方厘米.
22.解:连接如图:
23.解:从上面看:着色的有6个正方形,
从前面看着色的有6个正方形,
从后面看着色的有6个正方形,
从左面看着色的有6个正方形,
从右面看着色的有6个正方形,
共5×6=30个,
∵小正方体的一个侧面的面积为1,
∴30×1=30,
答:此几何体要着色的面积是30.
24.解:(1)AB与GB的位置关系是垂直;
(2)CB与GB的位置关系是垂直;
(3)AB与BC的位置关系是重合,理由解释为:过一点有且只有一条直线与已知直线垂直.
故答案为:垂直,垂直,重合,过一点有且只有一条直线与已知直线垂直.
25.解:如图所示:
26.解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.
绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3.
故形成的几何体的体积是36πcm3或48πcm3.
27.解:如图所示:
一.选择题
1.下列第一行所示的四个图形,每个图形均是由四种简单的图形a、b、c、d(圆、直线、三角形、长方形)中的两种组成.例如由a、b组成的图形记作a⊙b,那么由此可知,下列第二行的图中可以记作a⊙d的是( )
A. B.
C. D.
2.将下左图直角三角形ABC绕直角边AC旋转一周,所得几何体从正面是( )
A. B. C. D.
3.将如图所示的平面图形绕轴旋转一周,可以得到的立体图形是( )
A. B.
C. D.
4.由5个棱长为1的小正方体组成的几何体如图放置,一面着地,两面靠墙.如果要将露出来的部分涂色,则涂色部分的面积为( )
A.9 B.11 C.14 D.18
5.正五边形对角线的条数为( )
A.5条 B.6条 C.7条 D.8条
6.下列图形中,是正方体的展开图是( )
A.①② B.③④ C.③ D.④
7.如图的几何体由5个相同的小正方体搭成.从正面看,这个几何体的形状是( )
A. B.
C. D.
8.棱长分别是3、5、8的三个正方体被粘合在一起,在这些用各种方式粘合在一起的几何体中,表面积最小的那个几何体的表面积是( )
A.570 B.502 C.530 D.538
9.如图所示的四个图形中,( )不是正方体的表面展开图.
A. B.
C. D.
10.已知如图,则不含阴影部分的矩形的个数是( )
A.15 B.24 C.25 D.26
二.填空题
11.一个直角三角形绕其直角边旋转一周得到的几何体是 .
12.用一张正方形的纸片剪出一个面积最大的圆形纸片,如果已知正方形的边长是4厘米,那么这个圆形的面积是 平方厘米.
13.五棱柱有 个面.
14.以立方体的8个顶点中的任意3个顶点为顶点的三角形中,正三角形的个数为 .
15.在朱自清的《春》中有描写春雨“像牛毛,像细丝,密密地斜织着”的语句,这里把雨看成了线,这说明 .
16.如图,有两个相同的长方体纸盒,它们的长、宽、高分别是12cm,6cm,2cm,现要用这两个纸盒搭成一个大长方体,搭成的大长方体的表面积最小为 cm2.
17.如图,5个边长为1cm的正方体摆在桌子上,则露在表面的部分的面积为 cm2.
18.一个圆被分成四个扇形,若各个扇形的面积之比为4:2:1:3,则最小的扇形的圆心角的度数为 .
19.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是 .
20.一个无盖的长方形包装盒展开后如图所示(单位:cm),则其容积为 cm3.
三.解答题
21.用彩带捆扎一个圆柱形的蛋糕盒(如图,打结处正好是底面圆心,打结用去彩带18cm.
(1)扎这个盒子至少用去彩带多少厘米?
(2)这个蛋糕盒子的体积是多少立方厘米?
(3)蛋糕的直径比盒子直径少3cm,高比盒子矮5cm,张琳打开盒子,沿着蛋糕底面的直径垂直切开,平均分成两部分,这时蛋糕的表面积增加多少平方厘米?
22.各个花瓶的表面可以看作由哪个平面图形绕虚线旋转一周而得到?用线连一连.
23.如图所示的几何体是由若干个相同的小正方体搭建而成的(第一层,1个;第二层3个;第3层,6个),小正方体的一个侧面的面积为1.今要用红颜色给这个几何体的表面着色(但底部不着色),要着色的面积是多少?
24.在把如图折叠成正方体后,
(1)AB与GB的位置关系是 ;
(2)CB与GB的位置关系是 ;
(3)AB与BC的位置关系是 ,理由解释为 .
25.如图所示,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成一正方体的表面展开图.(填出两种答案)
26.在一个长方形中,长和宽分别为4cm、3cm,若该长方形绕着它的一边旋转一周,形成的几何体的体积是多少?(结果用π表示)
27.如图是一个正方体纸盒的展开图,请把﹣10,7,10,﹣2,﹣7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数.
参考答案与试题解析
一.选择题
1.解:根据题意,知a代表长方形,d代表直线,所以记作a⊙d的图形是长方形和直线的组合,
故选:A.
2.解:直角三角形ABC绕直角边AC旋转一周可得圆锥,从正面看图形是等腰三角形.
故选:D.
3.解:绕直线l旋转一周,可以得到圆台,
故选:B.
4.解:由图可知涂色部分是从上、前、右三个方向所涂面积相加,即涂色部分面积为4+4+3=11,
故选:B.
5.解:由题意得:5(5﹣3)÷2=5,
故选:A.
6.解:①中间4个正方形是“田字形”,不是正方体展开图;
②折叠后有两个正方形重合,不是正方体展开图;
③不符合正方体展开图;
④符合正方体展开图;
故,是正方体展开图的是④.
故选:D.
7.解:从正面看第一层是三个小正方形,第二层中间一个小正方形,
故选:A.
8.解:(3×3+5×5+8×8)×6﹣(3×3)×4﹣(5×5)×2
=98×6﹣9×4﹣25×2
=588﹣36﹣50
=502.
故选:B.
9.解:A、折叠后第二行两个面无法折起来,不能折成正方体;B、C、D都是正方体的展开图.
故选:A.
10.解:根据以上分析不含阴影的矩形个数为26个.
故选:D.
二.填空题
11.解:以直角三角形的一条直角边所在直线为对称轴旋转一周,得到一个圆锥,
故答案为:圆锥.
12.解:∵正方形的边长是4厘米,
∴剪出的最大的圆直径为4厘米,
半径=2厘米,
所以,圆的面积=πr2=3.14×22=12.56(平方厘米).
故答案为:12.56.
13.解:∵五棱柱有2个底面,5个侧面,
∴五棱柱的面数为7.
故答案为:7.
14.解:如图所示:
正三角形的各边必为立方体各面的对角线,有△ADF,△ADH,△AFH,△BCE,△BCG,△BEG,△CEG,△DFH共8个正三角形.
故答案为:8.
15.解:“像牛毛,像细丝,密密地斜织着”的语句,这里把雨看成了线,这说明点动成线.
故答案为:点动成线.
16.解:(1)图1中,长方体的高为4,表面积=2(12×6+12×4+4×6)=288cm2.
图2中,长为24,表面积=2(24×6+24×2+6×2)=408cm2.
图3中,宽为12,表面积=2(12×12+12×2+12×2)=384cm2.
∴图1的表面积最小.
故答案为:288.
17.解:根据以上分析故露在表面的部分的面积为16cm2.故
答案为16.
18.解:∵扇形A,B,C,D的面积之比为4:2:1:3,
∴其所占扇形比分别为:,
∴最小的扇形的圆心角是360°×=36°.
故答案为:36°.
19.解:由图1可得,“中”和“的”相对;“国”和“我”相对;“梦”和“梦”相对;
由图2可得,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格时,“国”在下面,则这时小正方体朝上一面的字是“我”.
故答案为:我.
20.解:20﹣15=5(cm),
15﹣5=10(cm),
26﹣10=16(cm),
16×10×5=800(cm3).
答:其容积为800cm3.
故答案为:800.
三.解答题
21.解:(1)2(30×2+20×2)+18=218cm,
答:扎这个盒子至少用去彩带218cm;
(2)由圆柱的体积,得
3.14×()2×20=14130(cm3),
答:这个蛋糕盒子的体积是14130cm3
(3)蛋糕的直径是30﹣3=27cm,蛋糕的高是20﹣5=15cm,
截面的面积是27×15×2=810cm2.
答:蛋糕的表面积增加810平方厘米.
22.解:连接如图:
23.解:从上面看:着色的有6个正方形,
从前面看着色的有6个正方形,
从后面看着色的有6个正方形,
从左面看着色的有6个正方形,
从右面看着色的有6个正方形,
共5×6=30个,
∵小正方体的一个侧面的面积为1,
∴30×1=30,
答:此几何体要着色的面积是30.
24.解:(1)AB与GB的位置关系是垂直;
(2)CB与GB的位置关系是垂直;
(3)AB与BC的位置关系是重合,理由解释为:过一点有且只有一条直线与已知直线垂直.
故答案为:垂直,垂直,重合,过一点有且只有一条直线与已知直线垂直.
25.解:如图所示:
26.解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.
绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3.
故形成的几何体的体积是36πcm3或48πcm3.
27.解:如图所示:
