2020-2021学年湘教版七年级下册数学《第4章 相交线与平行线》单元测试卷(word版,有答案)
文档属性
| 名称 | 2020-2021学年湘教版七年级下册数学《第4章 相交线与平行线》单元测试卷(word版,有答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 159.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 00:00:00 | ||
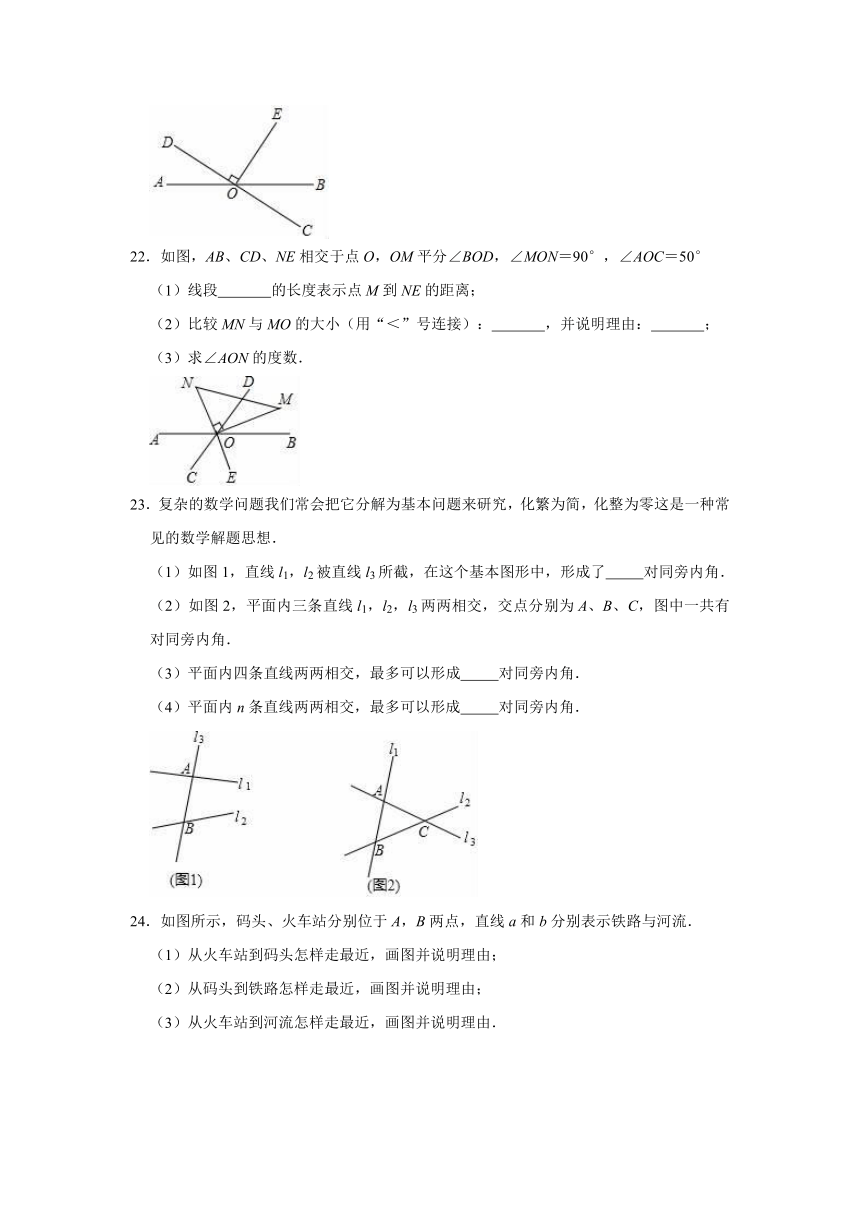
图片预览




文档简介
2020-2021学年湘教新版七年级下册数学《第4章 相交线与平行线》单元测试卷
一.选择题
1.平面上有3条直线,则交点可能是( )
A.1个 B.1个或3个
C.1个或2个或3个 D.0个或1个或2个或3个
2.如图,平面内∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD,则以下结论:
①∠AOE=∠DOE;②∠AOD+∠COB=180°;③∠COB﹣∠AOD=90°;④∠COE+∠BOF=180°.
其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.0个
3.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A. B.
C. D.
4.如图,经过直线a外一点O的4条直线中,与直线a相交的直线至少有( )
A.4条 B.3条 C.2条 D.1条
5.下列说法正确的是( )
A.同位角相等
B.在同一平面内,如果a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角
D.在同一平面内,如果a∥b,b∥c,则a∥c
6.如图,直线AB,CD交于点O,射线OM平分∠AOC,如果∠AOD=104°,那么∠BOM等于( )
A.38° B.104° C.140° D.142°
7.如图,AC⊥BC,AC=4,点D是线段BC上的动点,则A、D两点之间的距离不可能是( )
A.3.5 B.4.5 C.5 D.5.5
8.如图,∠1和∠2不是同旁内角的是( )
A. B.
C. D.
9.如图,点E在射线AB上,要AD∥BC,只需( )
A.∠A=∠CBE B.∠A=∠C C.∠C=∠CBE D.∠A+∠D=180°
10.如图,已知AB∥CD,CE平分∠ACD,交AB于点B,∠ABE=150°,则∠A为( )
A.110° B.120° C.135° D.150°
二.填空题
11.如图,直线AB、CD相交于O,且∠AOC=2∠BOC,则∠AOD的度数为 .
12.如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是 .
13.如图,∠B的内错角是 .
14.同一平面内的三条直线,其交点的个数可能为 .
15.一平面内,两条直线的位置关系是 .
16.如图,直线a∥c,∠1=∠2,那么直线b、c的位置关系是 .
17.如图,要使AD∥BF,则需要添加的条件是 (写一个即可)
18.如图,EF∥AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,则∠FEC= °.
19.如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC= °.
20.如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:当m=2时,d的取值范围是 .
三.解答题
21.如图,直线AB、CD相交于O,OE⊥CD,且∠BOD的度数是∠AOD的5倍.
求:(1)∠AOD、∠BOD的度数;
(2)∠BOE的度数.
22.如图,AB、CD、NE相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°
(1)线段 的长度表示点M到NE的距离;
(2)比较MN与MO的大小(用“<”号连接): ,并说明理由: ;
(3)求∠AON的度数.
23.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
24.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
25.如图,已知,∠1=∠ABC=∠ADC,∠3=∠5,∠2=∠4,∠ABC+∠BCD=180°.将下列推理过程.
补充完整:
(1)∵∠1=∠ABC(已知),
∴AD∥ ,( )
(2)∵∠3=∠5(已知),
∴AB∥ ,( )
(3)∵∠ABC+∠BCD=180°(已知),
∴ ∥ ,( )
26.平面内有不重合的4条直线,请指出这4条直线交点个数的所有情况,并画出相应的草图.
27.如图,直线AB、CD相交于点O,OE平分∠AOC,OE⊥OF,∠AOE=32°.
(1)求∠DOB的度数;
(2)OF是∠AOD的角平分线吗?为什么?
参考答案与试题解析
一.选择题
1.解:3条直线的分布情况可能是:如图,
交点个数分别是0个或1个或2个或3个,
故选:D.
2.解:∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
而∠COE=∠BOE,
∴∠AOE=∠DOE,所以①正确;
∠AOD+∠COB=∠AOD+∠AOC+90°=90°+90°=180°,所以②正确;
∠COB﹣∠AOD=∠AOC+90°﹣∠AOD,
而∠AOC≠∠AOD,所以③不正确;
∵OF平分∠AOD,
∴∠AOF=∠DOF,
而∠AOE=∠DOE,
∴∠AOF+∠AOE=∠DOF+∠DOE=180°,即点F、O、E共线,
∵∠COE=∠BOE,
∴∠COE+∠BOF=180°,所以④正确.
故选:B.
3.解:线段AD的长表示点A到直线BC距离的是图D,
故选:D.
4.解:根据经过直线外一点有且只有一条直线和已知直线平行,得出如果有和直线a平行的,只能是一条,
即与直线a相交的直线至少有3条,
故选:B.
5.解:A、只有在两直线平行这一前提下,同位角才相等,故A选项错误;
B、在同一平面内,如果a⊥b,b⊥c,则a∥c,故B选项错误;
C、相等的角不一定是对顶角,因为对顶角还有位置限制,故C选项错误;
D、由平行公理的推论知,如果两条直线都和第三条直线平行,那么这两条直线也互相平行,故D选项正确.
故选:D.
6.解:∵∠AOD=104°,
∴∠AOC=76°,
∵射线OM平分∠AOC,
∴∠AOM=∠AOC=×76°=38°,
∴∠BOM=180°﹣∠AOM=180°﹣38°=142°.
故选:D.
7.解:∵AC⊥BC,AC=4,
∴AD≥AC,即AD≥4.
观察选项,只有选项A符合题意.
故选:A.
8.解:选项A、B、C中,∠1与∠2在两直线的之间,并且在第三条直线(截线)的同旁,是同旁内角;
选项D中,∠1与∠2的两条边都不在同一条直线上,不是同旁内角.
故选:D.
9.解:要AD∥BC,只需∠A=∠CBE,
故选:A.
10.解:∵∠ABE=150°,
∴∠ABC=30°,
又∵AB∥CD,
∴∠ABC=∠BCD=30°,
∵CE平分∠ACD,
∴∠ACD=2∠BCD=60°,
又∵AB∥CD,
∴∠A+∠ACD=180°,
∴∠A=180°﹣∠ACD=180°﹣60°=120°.
故选:B.
二.填空题
11.解:∵∠AOC+∠BOC=180°,
又已知∠AOC=2∠BOC,
∴3∠BOC=180°,
解得∠BOC=60°,
∴∠AOD=∠BOC=60°.
12.解:根据垂线段定理,连接直线外一点与直线上各点的所有线段中,垂线段最短,
∴沿AB开渠,能使所开的渠道最短.
故答案为:垂线段最短.
13.解:∠B的内错角是∠BAD;
故答案为:∠BAD.
14.解:如图,同一平面内的三条直线,其交点个数为:0个;1个;2个;3个.
故答案为:0、1、2、3.
15.解:同一平面内,两条直线的位置关系是:相交、平行或重合.
16.解:∵∠1=∠2,
∴a∥b,
∵a∥c,
∴b∥c.
故答案为:b∥c.
17.解:当∠A=∠EBC(或∠D=∠DCF或∠A+∠ABC=180°或∠D+∠BCD=180°)时,AD∥BF,
故答案为:∠A=∠EBC(答案不唯一).
18.解:∵AD∥BC,
∴∠ACB+∠DAC=180°,
∴∠ACB=180°﹣120°=60°,
∴∠BCF=∠ACB﹣∠ACF=60°﹣20°=40°,
∵CE平分∠BCF,
∴∠BCE=∠BCF=20°,
∵EF∥BC,
∴∠FEC=∠BCE=20°.
故答案为20.
19.解:∵∠AOD=132°,
∴∠COB=132°,
∵EO⊥AB,
∴∠EOB=90°,
∴∠COE=132°﹣90°=42°,
故答案为:42.
20.解:当d=3时,m=1;
当d=1时,m=3;
∴当1<d<3时,m=2,
故答案为:1<d<3.
三.解答题
21.解:(1)∵AB是直线(已知),
∴∠BOD+∠AOD=180°,
∵∠BOD的度数是∠AOD的5倍,
∴∠AOD=×180°=30°,∠BOD=×180°=150°.
(2)∵∠BOC=∠AOD=30°,OE⊥DC,
∴∠EOC=90°,
∴∠BOE=∠EOC﹣∠BOC=90°﹣30°=60°.
22.解:(1)线段MO的长度表示点M到NE的距离;
(2)比较MN与MO的大小为:MO<MN,是因为垂线段最短;
(3)∵∠BOD=∠AOC=50°,OM平分∠BOD,
∴∠BOM=25°,
∴∠AON=180°﹣∠BOM﹣∠MON=180°﹣25°﹣90°=65°.
故答案为:MO;MO<MN;垂线段最短.
23.解:因为两个交点可以形成2对同旁内角,而三个交点形成的同旁内角的对数为6对,
(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有3×2=6对同旁内角.
(3)平面内四条直线两两相交,交点最多为6个,最多可以形成4×(4﹣1)×(4﹣2)=24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
24.解:如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
25.解:(1)∵∠1=∠ABC(已知),
∴AD∥BC,(同位角相等两直线平行)
(2)∵∠3=∠5(已知),
∴AB∥CD,(内错角相等两直线平行)
(3)∵∠ABC+∠BCD=180°(已知),
∴AB∥CD(同旁内角互补两直线平行).
26.解:(1)当四条直线平行时,无交点,
(2)当三条平行,另一条与这三条不平行时,有3个交点,
(3)当两两直线平行时,有4个交点,
(4)当有两条直线平行,而另两条不平行时,有5个交点,
(5)当四条直线同交于一点时,只有1个交点,
(6)当四条直线两两相交,且不过同一点时,有6个交点,
(7)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点,
(8)当三条直线交于一点,第四条直线与其它三条直线有三个交点时,共有4个交点,
故4条直线交点个数为:0或1或3或4或5或6.
27.解:(1)∵OE平分∠AOC,
∴∠AOC=2∠AOE=64°,
∵∠DOB与∠AOC是对顶角,
∴∠DOB=∠AOC=64°;
(2)∵OE⊥OF,
∴∠EOF=90°,
∴∠AOF=∠EOF﹣∠AOE=58°,
∵∠AOD=180°﹣∠AOC=116°,
∴∠AOD=2∠AOF,
∴OF是∠AOD的角平分线.
一.选择题
1.平面上有3条直线,则交点可能是( )
A.1个 B.1个或3个
C.1个或2个或3个 D.0个或1个或2个或3个
2.如图,平面内∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD,则以下结论:
①∠AOE=∠DOE;②∠AOD+∠COB=180°;③∠COB﹣∠AOD=90°;④∠COE+∠BOF=180°.
其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.0个
3.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A. B.
C. D.
4.如图,经过直线a外一点O的4条直线中,与直线a相交的直线至少有( )
A.4条 B.3条 C.2条 D.1条
5.下列说法正确的是( )
A.同位角相等
B.在同一平面内,如果a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角
D.在同一平面内,如果a∥b,b∥c,则a∥c
6.如图,直线AB,CD交于点O,射线OM平分∠AOC,如果∠AOD=104°,那么∠BOM等于( )
A.38° B.104° C.140° D.142°
7.如图,AC⊥BC,AC=4,点D是线段BC上的动点,则A、D两点之间的距离不可能是( )
A.3.5 B.4.5 C.5 D.5.5
8.如图,∠1和∠2不是同旁内角的是( )
A. B.
C. D.
9.如图,点E在射线AB上,要AD∥BC,只需( )
A.∠A=∠CBE B.∠A=∠C C.∠C=∠CBE D.∠A+∠D=180°
10.如图,已知AB∥CD,CE平分∠ACD,交AB于点B,∠ABE=150°,则∠A为( )
A.110° B.120° C.135° D.150°
二.填空题
11.如图,直线AB、CD相交于O,且∠AOC=2∠BOC,则∠AOD的度数为 .
12.如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是 .
13.如图,∠B的内错角是 .
14.同一平面内的三条直线,其交点的个数可能为 .
15.一平面内,两条直线的位置关系是 .
16.如图,直线a∥c,∠1=∠2,那么直线b、c的位置关系是 .
17.如图,要使AD∥BF,则需要添加的条件是 (写一个即可)
18.如图,EF∥AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,则∠FEC= °.
19.如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC= °.
20.如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:当m=2时,d的取值范围是 .
三.解答题
21.如图,直线AB、CD相交于O,OE⊥CD,且∠BOD的度数是∠AOD的5倍.
求:(1)∠AOD、∠BOD的度数;
(2)∠BOE的度数.
22.如图,AB、CD、NE相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°
(1)线段 的长度表示点M到NE的距离;
(2)比较MN与MO的大小(用“<”号连接): ,并说明理由: ;
(3)求∠AON的度数.
23.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
24.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
25.如图,已知,∠1=∠ABC=∠ADC,∠3=∠5,∠2=∠4,∠ABC+∠BCD=180°.将下列推理过程.
补充完整:
(1)∵∠1=∠ABC(已知),
∴AD∥ ,( )
(2)∵∠3=∠5(已知),
∴AB∥ ,( )
(3)∵∠ABC+∠BCD=180°(已知),
∴ ∥ ,( )
26.平面内有不重合的4条直线,请指出这4条直线交点个数的所有情况,并画出相应的草图.
27.如图,直线AB、CD相交于点O,OE平分∠AOC,OE⊥OF,∠AOE=32°.
(1)求∠DOB的度数;
(2)OF是∠AOD的角平分线吗?为什么?
参考答案与试题解析
一.选择题
1.解:3条直线的分布情况可能是:如图,
交点个数分别是0个或1个或2个或3个,
故选:D.
2.解:∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
而∠COE=∠BOE,
∴∠AOE=∠DOE,所以①正确;
∠AOD+∠COB=∠AOD+∠AOC+90°=90°+90°=180°,所以②正确;
∠COB﹣∠AOD=∠AOC+90°﹣∠AOD,
而∠AOC≠∠AOD,所以③不正确;
∵OF平分∠AOD,
∴∠AOF=∠DOF,
而∠AOE=∠DOE,
∴∠AOF+∠AOE=∠DOF+∠DOE=180°,即点F、O、E共线,
∵∠COE=∠BOE,
∴∠COE+∠BOF=180°,所以④正确.
故选:B.
3.解:线段AD的长表示点A到直线BC距离的是图D,
故选:D.
4.解:根据经过直线外一点有且只有一条直线和已知直线平行,得出如果有和直线a平行的,只能是一条,
即与直线a相交的直线至少有3条,
故选:B.
5.解:A、只有在两直线平行这一前提下,同位角才相等,故A选项错误;
B、在同一平面内,如果a⊥b,b⊥c,则a∥c,故B选项错误;
C、相等的角不一定是对顶角,因为对顶角还有位置限制,故C选项错误;
D、由平行公理的推论知,如果两条直线都和第三条直线平行,那么这两条直线也互相平行,故D选项正确.
故选:D.
6.解:∵∠AOD=104°,
∴∠AOC=76°,
∵射线OM平分∠AOC,
∴∠AOM=∠AOC=×76°=38°,
∴∠BOM=180°﹣∠AOM=180°﹣38°=142°.
故选:D.
7.解:∵AC⊥BC,AC=4,
∴AD≥AC,即AD≥4.
观察选项,只有选项A符合题意.
故选:A.
8.解:选项A、B、C中,∠1与∠2在两直线的之间,并且在第三条直线(截线)的同旁,是同旁内角;
选项D中,∠1与∠2的两条边都不在同一条直线上,不是同旁内角.
故选:D.
9.解:要AD∥BC,只需∠A=∠CBE,
故选:A.
10.解:∵∠ABE=150°,
∴∠ABC=30°,
又∵AB∥CD,
∴∠ABC=∠BCD=30°,
∵CE平分∠ACD,
∴∠ACD=2∠BCD=60°,
又∵AB∥CD,
∴∠A+∠ACD=180°,
∴∠A=180°﹣∠ACD=180°﹣60°=120°.
故选:B.
二.填空题
11.解:∵∠AOC+∠BOC=180°,
又已知∠AOC=2∠BOC,
∴3∠BOC=180°,
解得∠BOC=60°,
∴∠AOD=∠BOC=60°.
12.解:根据垂线段定理,连接直线外一点与直线上各点的所有线段中,垂线段最短,
∴沿AB开渠,能使所开的渠道最短.
故答案为:垂线段最短.
13.解:∠B的内错角是∠BAD;
故答案为:∠BAD.
14.解:如图,同一平面内的三条直线,其交点个数为:0个;1个;2个;3个.
故答案为:0、1、2、3.
15.解:同一平面内,两条直线的位置关系是:相交、平行或重合.
16.解:∵∠1=∠2,
∴a∥b,
∵a∥c,
∴b∥c.
故答案为:b∥c.
17.解:当∠A=∠EBC(或∠D=∠DCF或∠A+∠ABC=180°或∠D+∠BCD=180°)时,AD∥BF,
故答案为:∠A=∠EBC(答案不唯一).
18.解:∵AD∥BC,
∴∠ACB+∠DAC=180°,
∴∠ACB=180°﹣120°=60°,
∴∠BCF=∠ACB﹣∠ACF=60°﹣20°=40°,
∵CE平分∠BCF,
∴∠BCE=∠BCF=20°,
∵EF∥BC,
∴∠FEC=∠BCE=20°.
故答案为20.
19.解:∵∠AOD=132°,
∴∠COB=132°,
∵EO⊥AB,
∴∠EOB=90°,
∴∠COE=132°﹣90°=42°,
故答案为:42.
20.解:当d=3时,m=1;
当d=1时,m=3;
∴当1<d<3时,m=2,
故答案为:1<d<3.
三.解答题
21.解:(1)∵AB是直线(已知),
∴∠BOD+∠AOD=180°,
∵∠BOD的度数是∠AOD的5倍,
∴∠AOD=×180°=30°,∠BOD=×180°=150°.
(2)∵∠BOC=∠AOD=30°,OE⊥DC,
∴∠EOC=90°,
∴∠BOE=∠EOC﹣∠BOC=90°﹣30°=60°.
22.解:(1)线段MO的长度表示点M到NE的距离;
(2)比较MN与MO的大小为:MO<MN,是因为垂线段最短;
(3)∵∠BOD=∠AOC=50°,OM平分∠BOD,
∴∠BOM=25°,
∴∠AON=180°﹣∠BOM﹣∠MON=180°﹣25°﹣90°=65°.
故答案为:MO;MO<MN;垂线段最短.
23.解:因为两个交点可以形成2对同旁内角,而三个交点形成的同旁内角的对数为6对,
(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有3×2=6对同旁内角.
(3)平面内四条直线两两相交,交点最多为6个,最多可以形成4×(4﹣1)×(4﹣2)=24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
24.解:如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
25.解:(1)∵∠1=∠ABC(已知),
∴AD∥BC,(同位角相等两直线平行)
(2)∵∠3=∠5(已知),
∴AB∥CD,(内错角相等两直线平行)
(3)∵∠ABC+∠BCD=180°(已知),
∴AB∥CD(同旁内角互补两直线平行).
26.解:(1)当四条直线平行时,无交点,
(2)当三条平行,另一条与这三条不平行时,有3个交点,
(3)当两两直线平行时,有4个交点,
(4)当有两条直线平行,而另两条不平行时,有5个交点,
(5)当四条直线同交于一点时,只有1个交点,
(6)当四条直线两两相交,且不过同一点时,有6个交点,
(7)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点,
(8)当三条直线交于一点,第四条直线与其它三条直线有三个交点时,共有4个交点,
故4条直线交点个数为:0或1或3或4或5或6.
27.解:(1)∵OE平分∠AOC,
∴∠AOC=2∠AOE=64°,
∵∠DOB与∠AOC是对顶角,
∴∠DOB=∠AOC=64°;
(2)∵OE⊥OF,
∴∠EOF=90°,
∴∠AOF=∠EOF﹣∠AOE=58°,
∵∠AOD=180°﹣∠AOC=116°,
∴∠AOD=2∠AOF,
∴OF是∠AOD的角平分线.
