七年级数学7.1.2三角形的高.中线.角平分线
文档属性
| 名称 | 七年级数学7.1.2三角形的高.中线.角平分线 |

|
|
| 格式 | zip | ||
| 文件大小 | 333.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-17 00:00:00 | ||
图片预览

文档简介
(共27张PPT)
义务教育课程标准实验教科书 数学 七年级下册
晋梅中学 吴灿标
7.1.2三角形的高、中线与角平分线
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
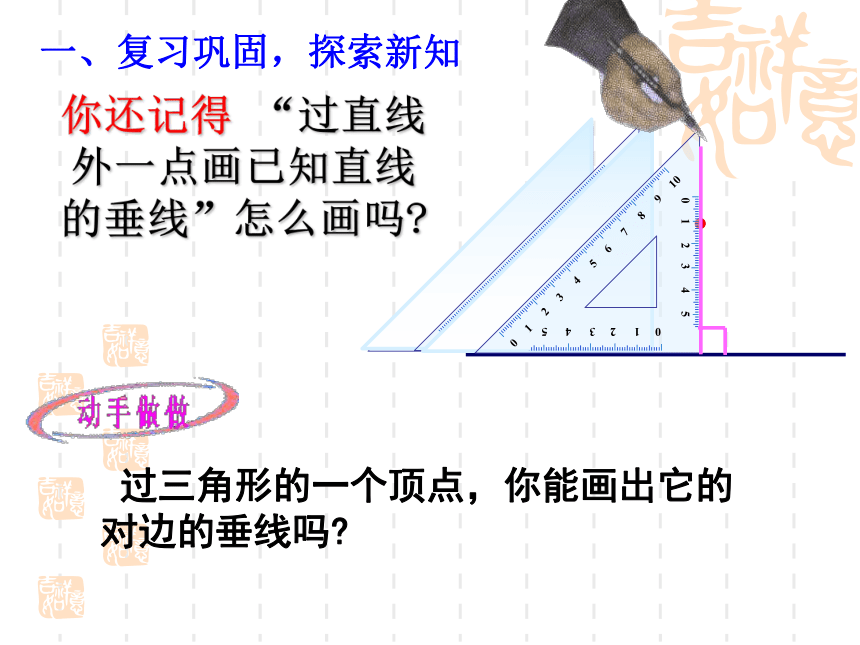
你还记得 “过直线外一点画已知直线的垂线”怎么画吗
一、复习巩固,探索新知
过三角形的一个顶点,你能画出它的
对边的垂线吗
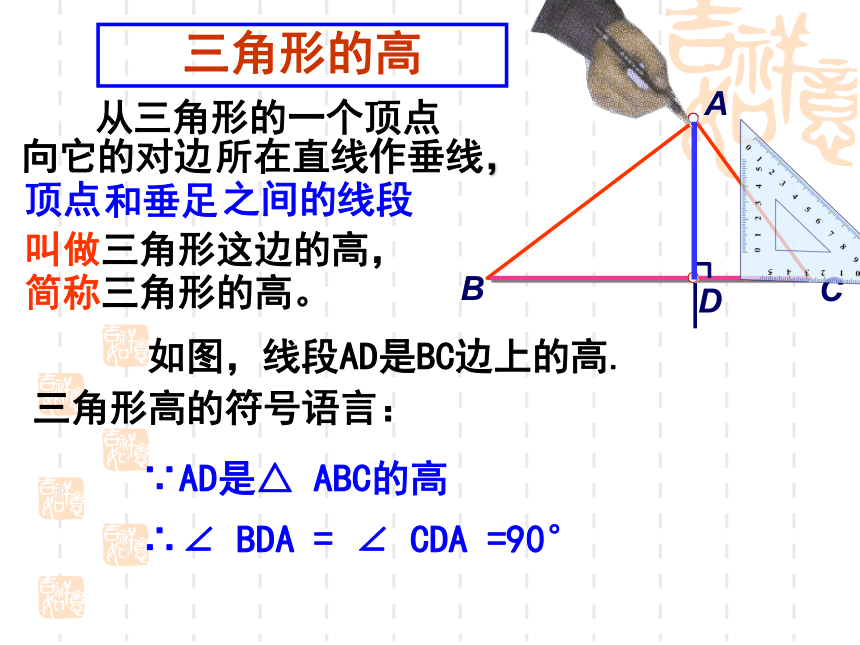
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形这边的高,
简称三角形的高。
如图,线段AD是BC边上的高.
三角形高的符号语言:
∵AD是△ ABC的高
∴∠ BDA = ∠ CDA =90°
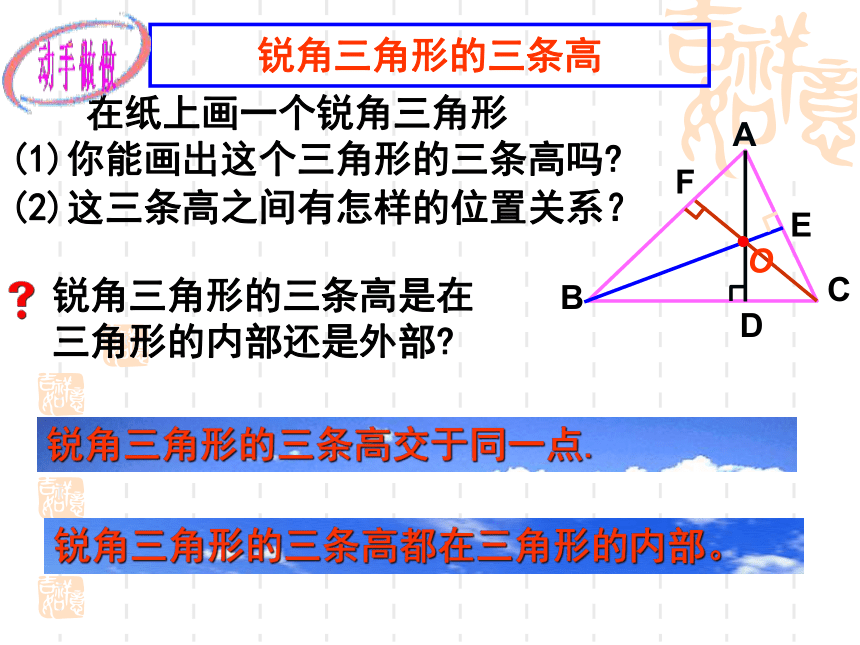
锐角三角形的三条高
在纸上画一个锐角三角形
(1)你能画出这个三角形的三条高吗
(2)这三条高之间有怎样的位置关系?
锐角三角形的三条高交于同一点.
O
锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高都在三角形的内部。
A
B
C
D
E
F
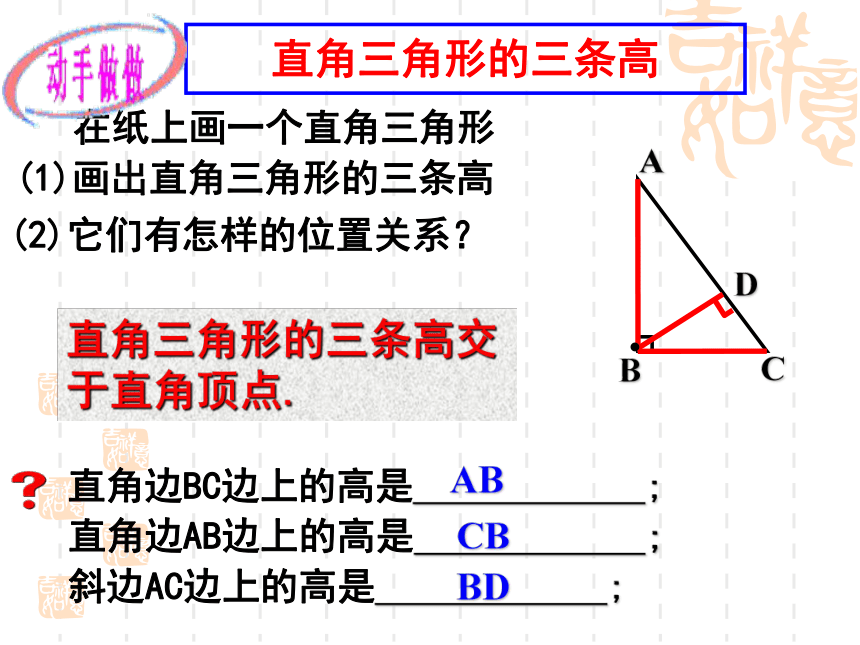
直角三角形的三条高
在纸上画一个直角三角形
A
B
C
(1)画出直角三角形的三条高
直角边BC边上的高是 ;
AB
直角边AB边上的高是 ;
CB
(2)它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
D
斜边AC边上的高是 ;
BD
●
●
B
A
C
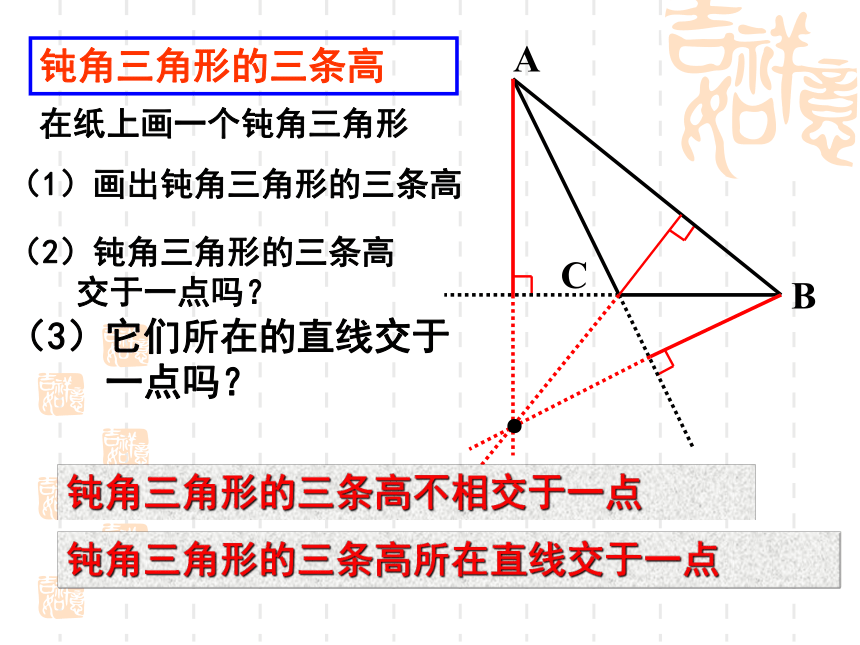
钝角三角形的三条高
在纸上画一个钝角三角形
(1)画出钝角三角形的三条高
(2)钝角三角形的三条高
交于一点吗?
(3)它们所在的直线交于
一点吗?
钝角三角形的三条高不相交于一点
钝角三角形的三条高所在直线交于一点
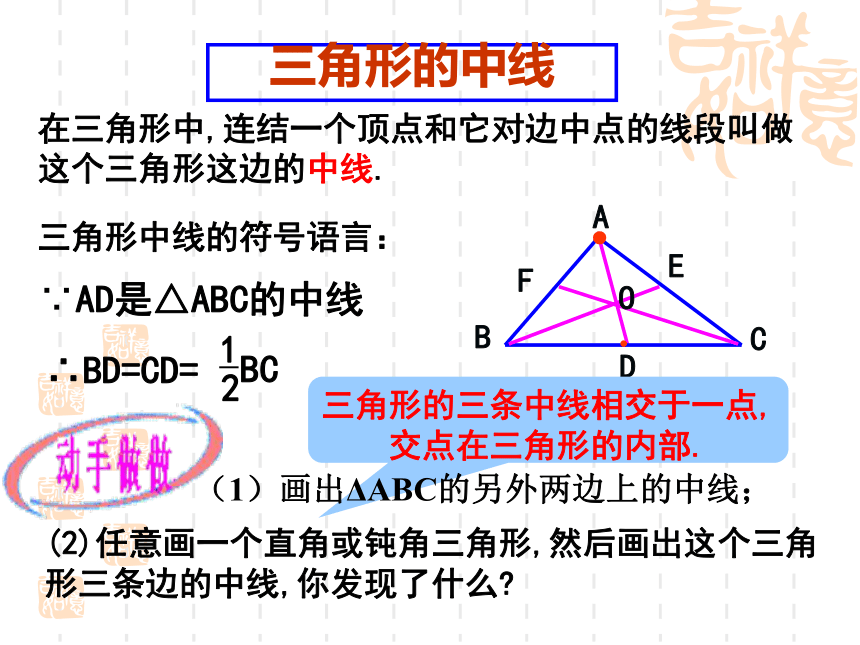
三角形的中线
在三角形中,连结一个顶点和它对边中点的线段叫做这个三角形这边的中线.
A
B
C
D
∵AD是△ABC的中线
∴BD=CD=
1
2
BC
(2)任意画一个直角或钝角三角形,然后画出这个三角形三条边的中线,你发现了什么
●
●
三角形的三条中线相交于一点,交点在三角形的内部.
三角形中线的符号语言:
E
F
O
(1)画出ΔABC的另外两边上的中线;
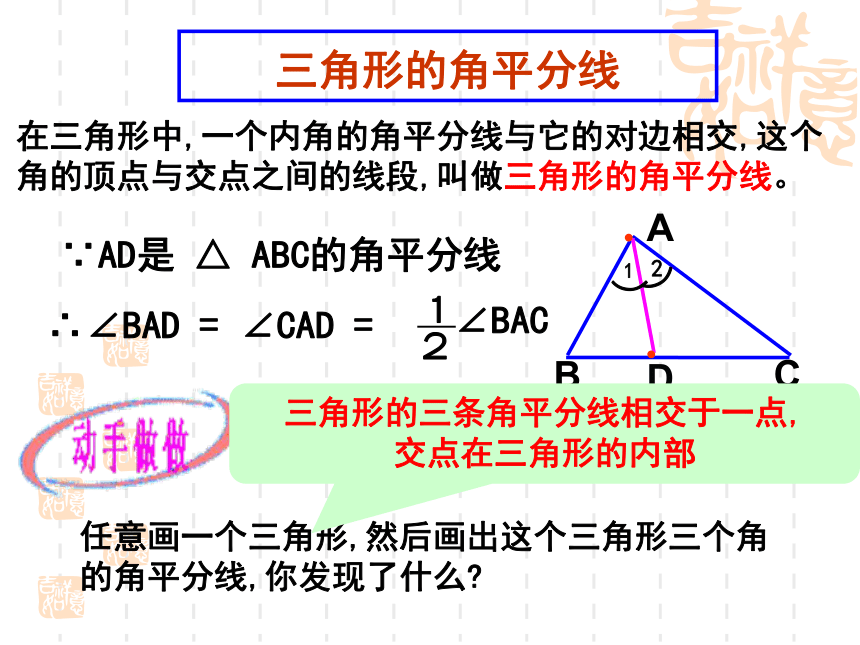
三角形的角平分线
A
B
C
D
∵AD是 △ ABC的角平分线
∴∠BAD = ∠CAD =
1
2
∠BAC
任意画一个三角形,然后画出这个三角形三个角的角平分线,你发现了什么
●
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线。
●
三角形的三条角平分线相交于一点,
交点在三角形的内部
︶
︶
1
2
三角形的角平分线与角的平分线有什么区别?
思考
三角形的角平分线是一条线段 , 角的平分线是一条射线
练一练
如图,在⊿ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法那些是正确的,哪些是错误的
⌒
⌒
A
B
C
D
E
1
2
F
G
H
①AD是⊿ABE的角平分线 ( )
②BE是⊿ABD边AD上的中线( )
③BE是⊿ABC边AC上的中线( )
④CH是⊿ACD边AD上的高 ( )
三角形的高、中线与角平分线都是线段
×
×
×
√
拓展练习
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
1.下列各组图形中,哪一组中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
B
D
拓展练习
CE
BC
∠CAD
∠BAC
∠AFC
4.填空:如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= = 90°
拓展练习
5.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有性质( )
A.是边BB′上的中线
B.是边BB′上的高
C.是∠BAB′的角平分线
D.以上三种性质合一
D
拓展练习
6.如图2所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BD=EC
D.∠C的对边是DE
C
通过本节课的学习,你有哪些收获?
小结
练习拓展
AF
CD
AC
3.填空:
(1)如图1,AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE= 。
(2)如图2, AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 。
∠2
∠ABC
∠4
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴ = _____ = _____
∴∠ACB=2______=2______
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
角平分线的符号语言
小结:三角形的高
从三角形中的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这边的高
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
三角形的中线
A
C
B
●
●
D
连结△ABC的顶点A和它所对的边BC的中点D,
线段AD叫做△ ABC的边BC上的中线。
(1)画出ΔABC的另外两边上的中线;
(2)说出哪条线段是ΔABC的哪条边上的中线;
观察ΔABC的三条中线,说说你的发现。
把刚才的锐角三角形换成直角三角形或钝角三角形,结果又怎么样呢?
三角形的三条中线在三角形的内部交于一点
E
F
●
●
●
●
●
三角形的角平分线
A
C
B
D
●
●
F
E
●
●
●
●
画∠A的平分线AD,交∠A所对的边BC于点D,
线段AD叫做ΔABC的角平分线。
画出ΔABC的另外两条角平分线;
观察三条角平分线,说说你的发现。
画一画想一想
三角形的三条角平分线在三角形的内部交于一点
对于其它的任意三角形是不是也有同样的结果?
1、下列各个图形中,哪一个图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
练一练
2、填空:p66
(1)如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE= 。
(2)如图(2), AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 。
D
3.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:p69
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
(4)SΔABC= 。
CE
BE
∠CAD
∠BAC
∠AFC
BC AF
1、在ΔABC中,CD是中线,已知BC-AC=5cm, ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
拓展
2、三角形的一条中线是否将这个三角形分成面积相等的两个三角形 为什么
画一画
(1)画一个锐角 △ABC,过A点向它所对的边BC所在 的直线画垂线,垂足为D;
A
C
B
●
D
●
顶点
和垂足
之间的线段
叫做三角形的高。
如图, 线段AD是BC边上的高.
(2)你能画出其他两边上的高吗?
通过画图你发现了什么?
三角形的三条高线交于一点
●
●
●
●
●
H
F
E
三角形的高
大挑战
你能画出直角三角形和钝角三角形的三条高吗?
●
●
观察直角三角形和钝角三角形的三条高,你又有什么发现?
讨论
三角形的三条高线交于一点
三角形的三条高线所在的直线交于一点
A
B
C
B
A
C
义务教育课程标准实验教科书 数学 七年级下册
晋梅中学 吴灿标
7.1.2三角形的高、中线与角平分线
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
你还记得 “过直线外一点画已知直线的垂线”怎么画吗
一、复习巩固,探索新知
过三角形的一个顶点,你能画出它的
对边的垂线吗
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形这边的高,
简称三角形的高。
如图,线段AD是BC边上的高.
三角形高的符号语言:
∵AD是△ ABC的高
∴∠ BDA = ∠ CDA =90°
锐角三角形的三条高
在纸上画一个锐角三角形
(1)你能画出这个三角形的三条高吗
(2)这三条高之间有怎样的位置关系?
锐角三角形的三条高交于同一点.
O
锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高都在三角形的内部。
A
B
C
D
E
F
直角三角形的三条高
在纸上画一个直角三角形
A
B
C
(1)画出直角三角形的三条高
直角边BC边上的高是 ;
AB
直角边AB边上的高是 ;
CB
(2)它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
D
斜边AC边上的高是 ;
BD
●
●
B
A
C
钝角三角形的三条高
在纸上画一个钝角三角形
(1)画出钝角三角形的三条高
(2)钝角三角形的三条高
交于一点吗?
(3)它们所在的直线交于
一点吗?
钝角三角形的三条高不相交于一点
钝角三角形的三条高所在直线交于一点
三角形的中线
在三角形中,连结一个顶点和它对边中点的线段叫做这个三角形这边的中线.
A
B
C
D
∵AD是△ABC的中线
∴BD=CD=
1
2
BC
(2)任意画一个直角或钝角三角形,然后画出这个三角形三条边的中线,你发现了什么
●
●
三角形的三条中线相交于一点,交点在三角形的内部.
三角形中线的符号语言:
E
F
O
(1)画出ΔABC的另外两边上的中线;
三角形的角平分线
A
B
C
D
∵AD是 △ ABC的角平分线
∴∠BAD = ∠CAD =
1
2
∠BAC
任意画一个三角形,然后画出这个三角形三个角的角平分线,你发现了什么
●
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线。
●
三角形的三条角平分线相交于一点,
交点在三角形的内部
︶
︶
1
2
三角形的角平分线与角的平分线有什么区别?
思考
三角形的角平分线是一条线段 , 角的平分线是一条射线
练一练
如图,在⊿ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法那些是正确的,哪些是错误的
⌒
⌒
A
B
C
D
E
1
2
F
G
H
①AD是⊿ABE的角平分线 ( )
②BE是⊿ABD边AD上的中线( )
③BE是⊿ABC边AC上的中线( )
④CH是⊿ACD边AD上的高 ( )
三角形的高、中线与角平分线都是线段
×
×
×
√
拓展练习
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
1.下列各组图形中,哪一组中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
B
D
拓展练习
CE
BC
∠CAD
∠BAC
∠AFC
4.填空:如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= = 90°
拓展练习
5.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有性质( )
A.是边BB′上的中线
B.是边BB′上的高
C.是∠BAB′的角平分线
D.以上三种性质合一
D
拓展练习
6.如图2所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BD=EC
D.∠C的对边是DE
C
通过本节课的学习,你有哪些收获?
小结
练习拓展
AF
CD
AC
3.填空:
(1)如图1,AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE= 。
(2)如图2, AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 。
∠2
∠ABC
∠4
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴ = _____ = _____
∴∠ACB=2______=2______
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
角平分线的符号语言
小结:三角形的高
从三角形中的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这边的高
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
三角形的中线
A
C
B
●
●
D
连结△ABC的顶点A和它所对的边BC的中点D,
线段AD叫做△ ABC的边BC上的中线。
(1)画出ΔABC的另外两边上的中线;
(2)说出哪条线段是ΔABC的哪条边上的中线;
观察ΔABC的三条中线,说说你的发现。
把刚才的锐角三角形换成直角三角形或钝角三角形,结果又怎么样呢?
三角形的三条中线在三角形的内部交于一点
E
F
●
●
●
●
●
三角形的角平分线
A
C
B
D
●
●
F
E
●
●
●
●
画∠A的平分线AD,交∠A所对的边BC于点D,
线段AD叫做ΔABC的角平分线。
画出ΔABC的另外两条角平分线;
观察三条角平分线,说说你的发现。
画一画想一想
三角形的三条角平分线在三角形的内部交于一点
对于其它的任意三角形是不是也有同样的结果?
1、下列各个图形中,哪一个图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
练一练
2、填空:p66
(1)如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE= 。
(2)如图(2), AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 。
D
3.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:p69
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
(4)SΔABC= 。
CE
BE
∠CAD
∠BAC
∠AFC
BC AF
1、在ΔABC中,CD是中线,已知BC-AC=5cm, ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
拓展
2、三角形的一条中线是否将这个三角形分成面积相等的两个三角形 为什么
画一画
(1)画一个锐角 △ABC,过A点向它所对的边BC所在 的直线画垂线,垂足为D;
A
C
B
●
D
●
顶点
和垂足
之间的线段
叫做三角形的高。
如图, 线段AD是BC边上的高.
(2)你能画出其他两边上的高吗?
通过画图你发现了什么?
三角形的三条高线交于一点
●
●
●
●
●
H
F
E
三角形的高
大挑战
你能画出直角三角形和钝角三角形的三条高吗?
●
●
观察直角三角形和钝角三角形的三条高,你又有什么发现?
讨论
三角形的三条高线交于一点
三角形的三条高线所在的直线交于一点
A
B
C
B
A
C
