11.4 一元一次不等式 课件(共26张PPT)
文档属性
| 名称 | 11.4 一元一次不等式 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 00:00:00 | ||
图片预览







文档简介
第十一章 一元一次不等式与一元一次不等式组
4 一元一次不等式
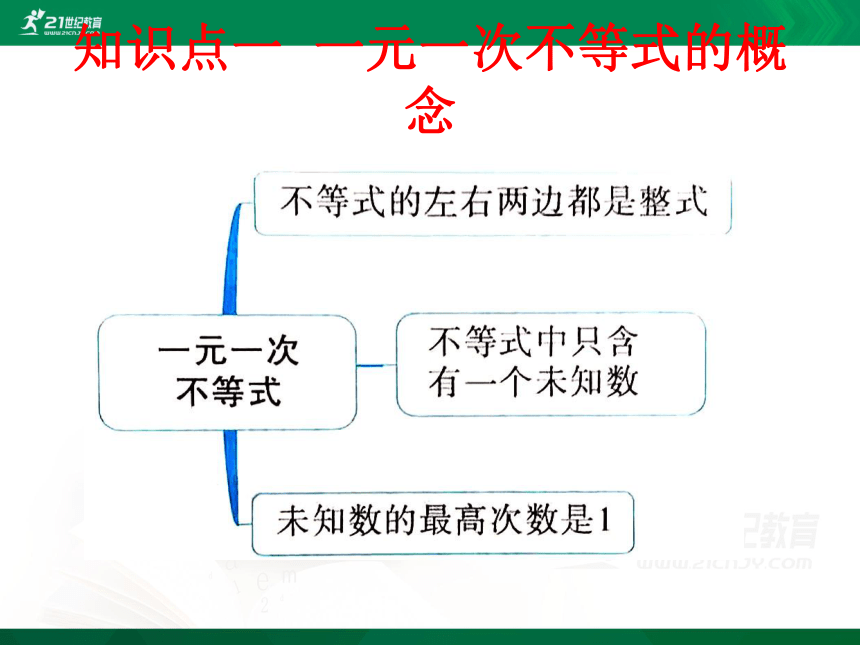
知识点一 一元一次不等式的概念
例1 下列不等式中,是一元一次不等式的是( )
A.x2+1>x b.-y+>y C.>1 D.5+4>8
例1 下列不等式中,是一元一次不等式的是( )
A.x2+1>x b.-y+>y C.>1 D.5+4>8
解析 A.未知数的最高次数是2,故本选项不符合题意;
B.是一元一次不等式,故本选项符合题意;
C.不等式的左边不是整式,故本选项不符合题意;
D.不含未知数,故本选项不符合题意.
故选B.
答案 B
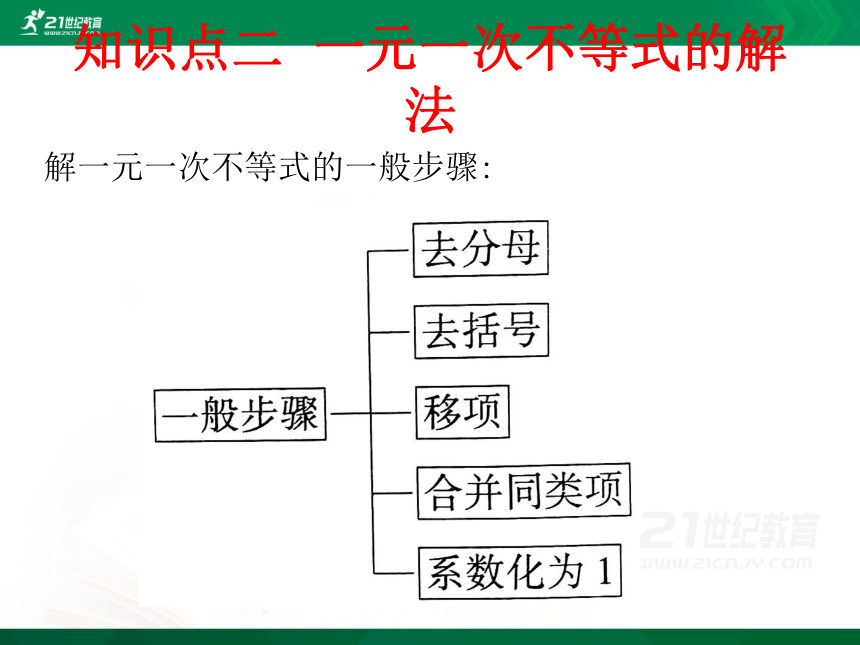
知识点二 一元一次不等式的解法
解一元一次不等式的一般步骤:
注意(1)一元一次不等式的解法与一元一次方程的解法的联系与区别如下表:
一元一次不等式
一元一次方程
去分母
根据不等式的基本性质2
根据等式的基本性质2
去括号
根据去括号法则
根据去括号法则
移项
根据不等式的基本性质1
根据等式的基本性质1
合并同类项
根据合并同类项法则
根据合并同类项法则
系数化为1
根据不等式的基本性质2,3
根据等式的基本性质2
解的情况
解集(含有多个解)
解(或根)(只有一个)
(2)去分母时千万不要漏乘.
(3)不等式的两边都乘(或除以)同一个负数,一定要改变不等号的方向.
(4)解不等式的五个步骤不一定都用到,顺序也可以改变.
(5)移项与解方程中的移项法则相同,注意改变所移项的符号,但不等号的方向不变.
例2 解不等式 ,并把此不等式的解集表示在如图所示的数轴上.
例2 解不等式 ,并把此不等式的解集表示在如图所示的数轴上.
解析 去分母,得3(x-1)+6≥2(2x+1),
去括号,得3x-3+6≥4x+2,
移项、合并同类项,得-x≥-1,
系数化为1,得x≤1,
在数轴上表示不等式的解集,如图所示:
例2 解不等式 ,并把此不等式的解集表示在如图所示的数轴上.
解析 去分母,得3(x-1)+6≥2(2x+1),
去括号,得3x-3+6≥4x+2,
移项、合并同类项,得-x≥-1,
系数化为1,得x≤1,
在数轴上表示不等式的解集,如图所示:
点拨 解一元一次不等式的一般步骤:1.去分母;2.去括号;3.移项;4.合并同类项;5.系数化为1.它与解一元一次方程的步骤一样,只是解不等式时,将不等式两边都乘(或除以)同一个负数,要改变不等号的方向.
知识点三 一元一次不等式的实际应用
列一元一次不等式解应用题的步骤
审
认真审题,找出已知量和未知量,并找出它们之间的关系
设
设出适当的未知数
列
根据题中的不等关系列出不等式
解
解不等式求出其解集
验
检验所求出的不等式的解集是否符合问题的实际意义
答
写出答案
列一元一次不等式解应用题的步骤
审
认真审题,找出已知量和未知量,并找出它们之间的关系
设
设出适当的未知数
列
根据题中的不等关系列出不等式
解
解不等式,求出其解集
验
检验所求出的不等式的解集是否符合问题的实际意义
答
写出答案
温馨
提示
(1)审题是解决问题的基础,根据不等关系列出不等式是解题的关键;
(2)在设未知数时,不可出现“至少”“至多”“不超过”等词语
例3 商店以7元/件的进价购进某种文具1000件,按10元/件的售价销售了500件现对剩下的这种文具进行降价销售,如果要保证总利润不低于2000元,那么剩下的这种文具最低定价是多少元?
例3 商店以7元/件的进价购进某种文具1000件,按10元/件的售价销售了500件现对剩下的这种文具进行降价销售,如果要保证总利润不低于2000元,那么剩下的这种文具最低定价是多少元?
解析 设剩下的这种文具定价为x元/件,根据题意,
得500×(10-7)+(1000-500)(x-7)≥2000,解得x≥8
答:剩下的这种文具最低定价是8元.
例3 商店以7元/件的进价购进某种文具1000件,按10元/件的售价销售了500件现对剩下的这种文具进行降价销售,如果要保证总利润不低于2000元,那么剩下的这种文具最低定价是多少元?
解析 设剩下的这种文具定价为x元/件,根据题意,
得500×(10-7)+(1000-500)(x-7)≥2000,解得x≥8
答:剩下的这种文具最低定价是8元.
点拨 设剩下的这种文具定价为x元/件,根据总利润=单件利润×销售数量,结合总利润不低于2000元,即可得出关于x的一元一次不等式,解之取其最小值即可得出答案.
经典例题
题型一 利用一元一次不等式解决代数问题
题型一 利用一元一次不等式解决代数问题
题型一 利用一元一次不等式解决代数问题
题型二 一元一次不等式与方程(组)的综合应用
例2 已知关于x,y的二元一次方程组 ,的解
满足x+y>3,求满足条件的m的取值范围.
题型二 一元一次不等式与方程(组)的综合应用
例2 已知关于x,y的二元一次方程组 ,的解
满足x+y>3,求满足条件的m的取值范围.
解析
①-②,得x+y=3m-6,
∵x+y>3,∴3m-6>3∴m>3.
题型二 一元一次不等式与方程(组)的综合应用
例2 已知关于x,y的二元一次方程组 ,的解
满足x+y>3,求满足条件的m的取值范围.
解析
①-②,得x+y=3m-6,
∵x+y>3,∴3m-6>3∴m>3.
点拨 方程组的两个方程相减表示出x+y,代入已知不等式即可求出m的取值范围.
易错易混
易错点 确定不等式的特殊解时易丢解
求不等式的特殊解是一类常见题型,主要有“整数解”“非负整数解”“非正整数解”等类型,而在这些类型的题目中,0是最容易被忽略的.
例 求不等式 的非正整数解.
4 一元一次不等式
知识点一 一元一次不等式的概念
例1 下列不等式中,是一元一次不等式的是( )
A.x2+1>x b.-y+>y C.>1 D.5+4>8
例1 下列不等式中,是一元一次不等式的是( )
A.x2+1>x b.-y+>y C.>1 D.5+4>8
解析 A.未知数的最高次数是2,故本选项不符合题意;
B.是一元一次不等式,故本选项符合题意;
C.不等式的左边不是整式,故本选项不符合题意;
D.不含未知数,故本选项不符合题意.
故选B.
答案 B
知识点二 一元一次不等式的解法
解一元一次不等式的一般步骤:
注意(1)一元一次不等式的解法与一元一次方程的解法的联系与区别如下表:
一元一次不等式
一元一次方程
去分母
根据不等式的基本性质2
根据等式的基本性质2
去括号
根据去括号法则
根据去括号法则
移项
根据不等式的基本性质1
根据等式的基本性质1
合并同类项
根据合并同类项法则
根据合并同类项法则
系数化为1
根据不等式的基本性质2,3
根据等式的基本性质2
解的情况
解集(含有多个解)
解(或根)(只有一个)
(2)去分母时千万不要漏乘.
(3)不等式的两边都乘(或除以)同一个负数,一定要改变不等号的方向.
(4)解不等式的五个步骤不一定都用到,顺序也可以改变.
(5)移项与解方程中的移项法则相同,注意改变所移项的符号,但不等号的方向不变.
例2 解不等式 ,并把此不等式的解集表示在如图所示的数轴上.
例2 解不等式 ,并把此不等式的解集表示在如图所示的数轴上.
解析 去分母,得3(x-1)+6≥2(2x+1),
去括号,得3x-3+6≥4x+2,
移项、合并同类项,得-x≥-1,
系数化为1,得x≤1,
在数轴上表示不等式的解集,如图所示:
例2 解不等式 ,并把此不等式的解集表示在如图所示的数轴上.
解析 去分母,得3(x-1)+6≥2(2x+1),
去括号,得3x-3+6≥4x+2,
移项、合并同类项,得-x≥-1,
系数化为1,得x≤1,
在数轴上表示不等式的解集,如图所示:
点拨 解一元一次不等式的一般步骤:1.去分母;2.去括号;3.移项;4.合并同类项;5.系数化为1.它与解一元一次方程的步骤一样,只是解不等式时,将不等式两边都乘(或除以)同一个负数,要改变不等号的方向.
知识点三 一元一次不等式的实际应用
列一元一次不等式解应用题的步骤
审
认真审题,找出已知量和未知量,并找出它们之间的关系
设
设出适当的未知数
列
根据题中的不等关系列出不等式
解
解不等式求出其解集
验
检验所求出的不等式的解集是否符合问题的实际意义
答
写出答案
列一元一次不等式解应用题的步骤
审
认真审题,找出已知量和未知量,并找出它们之间的关系
设
设出适当的未知数
列
根据题中的不等关系列出不等式
解
解不等式,求出其解集
验
检验所求出的不等式的解集是否符合问题的实际意义
答
写出答案
温馨
提示
(1)审题是解决问题的基础,根据不等关系列出不等式是解题的关键;
(2)在设未知数时,不可出现“至少”“至多”“不超过”等词语
例3 商店以7元/件的进价购进某种文具1000件,按10元/件的售价销售了500件现对剩下的这种文具进行降价销售,如果要保证总利润不低于2000元,那么剩下的这种文具最低定价是多少元?
例3 商店以7元/件的进价购进某种文具1000件,按10元/件的售价销售了500件现对剩下的这种文具进行降价销售,如果要保证总利润不低于2000元,那么剩下的这种文具最低定价是多少元?
解析 设剩下的这种文具定价为x元/件,根据题意,
得500×(10-7)+(1000-500)(x-7)≥2000,解得x≥8
答:剩下的这种文具最低定价是8元.
例3 商店以7元/件的进价购进某种文具1000件,按10元/件的售价销售了500件现对剩下的这种文具进行降价销售,如果要保证总利润不低于2000元,那么剩下的这种文具最低定价是多少元?
解析 设剩下的这种文具定价为x元/件,根据题意,
得500×(10-7)+(1000-500)(x-7)≥2000,解得x≥8
答:剩下的这种文具最低定价是8元.
点拨 设剩下的这种文具定价为x元/件,根据总利润=单件利润×销售数量,结合总利润不低于2000元,即可得出关于x的一元一次不等式,解之取其最小值即可得出答案.
经典例题
题型一 利用一元一次不等式解决代数问题
题型一 利用一元一次不等式解决代数问题
题型一 利用一元一次不等式解决代数问题
题型二 一元一次不等式与方程(组)的综合应用
例2 已知关于x,y的二元一次方程组 ,的解
满足x+y>3,求满足条件的m的取值范围.
题型二 一元一次不等式与方程(组)的综合应用
例2 已知关于x,y的二元一次方程组 ,的解
满足x+y>3,求满足条件的m的取值范围.
解析
①-②,得x+y=3m-6,
∵x+y>3,∴3m-6>3∴m>3.
题型二 一元一次不等式与方程(组)的综合应用
例2 已知关于x,y的二元一次方程组 ,的解
满足x+y>3,求满足条件的m的取值范围.
解析
①-②,得x+y=3m-6,
∵x+y>3,∴3m-6>3∴m>3.
点拨 方程组的两个方程相减表示出x+y,代入已知不等式即可求出m的取值范围.
易错易混
易错点 确定不等式的特殊解时易丢解
求不等式的特殊解是一类常见题型,主要有“整数解”“非负整数解”“非正整数解”等类型,而在这些类型的题目中,0是最容易被忽略的.
例 求不等式 的非正整数解.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
