小学数学西师大版六年级下 3.3反比例 课件(20张ppt)
文档属性
| 名称 | 小学数学西师大版六年级下 3.3反比例 课件(20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 09:36:26 | ||
图片预览







文档简介
反 比 例
说一说正比例的两个量的变化情况。
1、两个相关联的量。
2、一个量增加,另一个量也随着增加,一个量减少,另一个量也随着减少。
3、两个量的比值相同。
复 习 旧 知
两种 的量,一种量变化另一种量也随着变化,如果这两种量的______,这两种量叫做成正比例的量,它们的关系叫做________关系。
比值一定
正比例
相关联
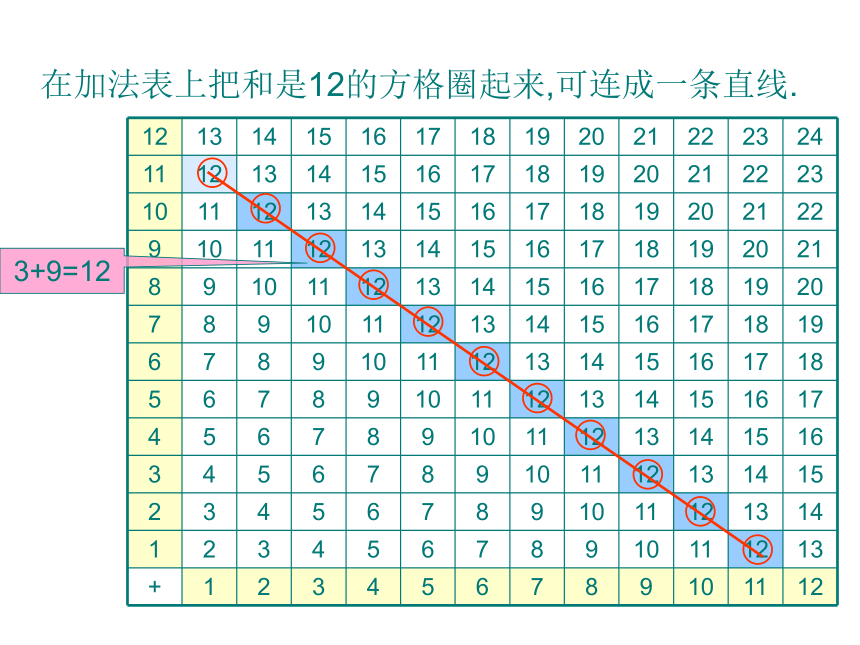
在加法表上把和是12的方格圈起来,可连成一条直线.
12
13
14
15
16
17
18
19
20
21
22
23
24
11
12
13
14
15
16
17
18
19
20
21
22
23
10
11
12
13
14
15
16
17
18
19
20
21
22
9
10
11
12
13
14
15
16
17
18
19
20
21
8
9
10
11
12
13
14
15
16
17
18
19
20
7
8
9
10
11
12
13
14
15
16
17
18
19
6
7
8
9
10
11
12
13
14
15
16
17
18
5
6
7
8
9
10
11
12
13
14
15
16
17
4
5
6
7
8
9
10
11
12
13
14
15
16
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
1
2
3
4
5
6
7
8
9
10
11
12
13
+
1
2
3
4
5
6
7
8
9
10
11
12
3+9=12
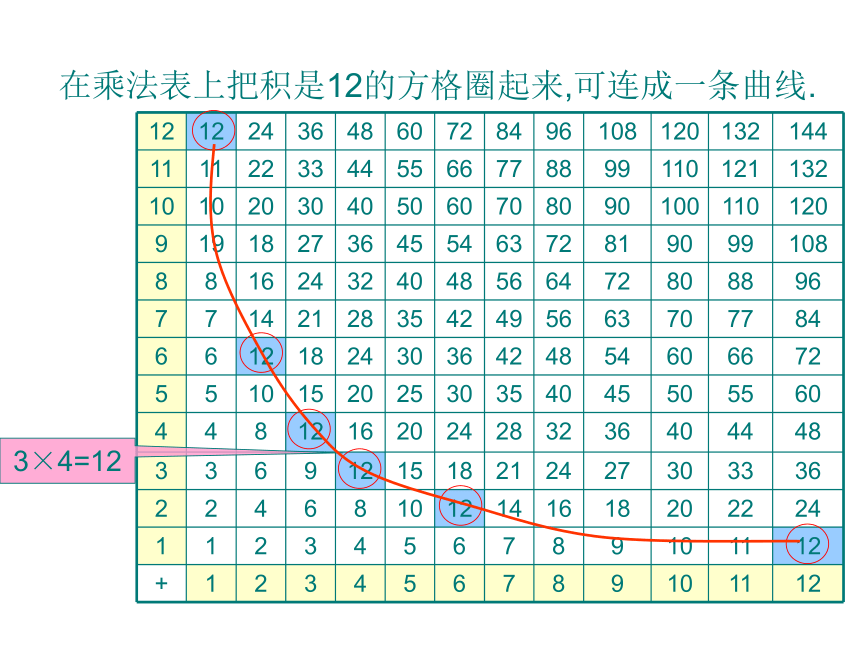
在乘法表上把积是12的方格圈起来,可连成一条曲线.
12
12
24
36
48
60
72
84
96
108
120
132
144
11
11
22
33
44
55
66
77
88
99
110
121
132
10
10
20
30
40
50
60
70
80
90
100
110
120
9
19
18
27
36
45
54
63
72
81
90
99
108
8
8
16
24
32
40
48
56
64
72
80
88
96
7
7
14
21
28
35
42
49
56
63
70
77
84
6
6
12
18
24
30
36
42
48
54
60
66
72
5
5
10
15
20
25
30
35
40
45
50
55
60
4
4
8
12
16
20
24
28
32
36
40
44
48
3
3
6
9
12
15
18
21
24
27
30
33
36
2
2
4
6
8
10
12
14
16
18
20
22
24
1
1
2
3
4
5
6
7
8
9
10
11
12
+
1
2
3
4
5
6
7
8
9
10
11
12
3×4=12
王叔叔要去游长城,不同的交通工具所需时间如下,请把表填完整。
时间/时
10
40
80
12
3
1.5
…
…
速度/千米
自行车
公共汽车
小汽车
速度是10,时间是12;
速度是40,时间是3;
速度是80,时间是1.5;
速度和所需时间是两种相关联的量,所需时间是随着速度的变化而变化的。
速度扩大,所需时间缩小。
速度缩小,所需时间扩大。
对应的速度和所需时间的积总是一定的:
10×12=120
40×3=120
80×1.5=120
(一定)
速度×时间=路程
有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
150
200
300
(1)表中有哪两种量?
表中有每杯的果汁量和分的杯数两种量
(2)分的杯数是怎样随着每杯的果汁量变化的?
每杯的果汁量扩大,分的杯数反而缩小;
每杯的果汁量缩小,分的杯数反而扩大;
每杯的果汁量和分的杯数的积是一定的
(3)它们的关系是什么?
每杯的果汁量× 分的杯数= 果汁总量(一定)
有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
150
200
300
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。 XY=K(一定)
(一定)
速度×时间=路程
每杯的果汁量× 分的杯数= 果汁总量(一定)
判定方法:
判定两个量是不是成反比例,主
要是看它们的积是不是一定的。
在加法表上把和是12的方格圈起来,可连成一条直线.
12
13
14
15
16
17
18
19
20
21
22
23
24
11
12
13
14
15
16
17
18
19
20
21
22
23
10
11
12
13
14
15
16
17
18
19
20
21
22
9
10
11
12
13
14
15
16
17
18
19
20
21
8
9
10
11
12
13
14
15
16
17
18
19
20
7
8
9
10
11
12
13
14
15
16
17
18
19
6
7
8
9
10
11
12
13
14
15
16
17
18
5
6
7
8
9
10
11
12
13
14
15
16
17
4
5
6
7
8
9
10
11
12
13
14
15
16
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
1
2
3
4
5
6
7
8
9
10
11
12
13
+
1
2
3
4
5
6
7
8
9
10
11
12
3+9=12
在乘法表上把积是12的方格圈起来,可连成一条曲线.
12
12
24
36
48
60
72
84
96
108
120
132
144
11
11
22
33
44
55
66
77
88
99
110
121
132
10
10
20
30
40
50
60
70
80
90
100
110
120
9
19
18
27
36
45
54
63
72
81
90
99
108
8
8
16
24
32
40
48
56
64
72
80
88
96
7
7
14
21
28
35
42
49
56
63
70
77
84
6
6
12
18
24
30
36
42
48
54
60
66
72
5
5
10
15
20
25
30
35
40
45
50
55
60
4
4
8
12
16
20
24
28
32
36
40
44
48
3
3
6
9
12
15
18
21
24
27
30
33
36
2
2
4
6
8
10
12
14
16
18
20
22
24
1
1
2
3
4
5
6
7
8
9
10
11
12
+
1
2
3
4
5
6
7
8
9
10
11
12
3×4=12
判断下面每题中的两种量是不是成反比例,并说明理由。
煤的总量一定,每天的烧煤量和能够烧的天数。
张伯伯骑自行车从家到县城,
骑自行车的速度和所需的时间。
判断下面每题中的两种量是不是成反比例,并说明理由。
生产电视机的总台数一定,每天生产的台数和所用的天数。
判断下面每题中的两种量是不是成反比例,并说明理由。
长方形的面积一定,它的长和宽。
判断下面每题中的两种量是不是成反比例,并说明理由。
铺地面积一定,方砖边长与所需块数。
判断下面每题中的两种量是不是成反比例,并说明理由。
谢 谢 !
说一说正比例的两个量的变化情况。
1、两个相关联的量。
2、一个量增加,另一个量也随着增加,一个量减少,另一个量也随着减少。
3、两个量的比值相同。
复 习 旧 知
两种 的量,一种量变化另一种量也随着变化,如果这两种量的______,这两种量叫做成正比例的量,它们的关系叫做________关系。
比值一定
正比例
相关联
在加法表上把和是12的方格圈起来,可连成一条直线.
12
13
14
15
16
17
18
19
20
21
22
23
24
11
12
13
14
15
16
17
18
19
20
21
22
23
10
11
12
13
14
15
16
17
18
19
20
21
22
9
10
11
12
13
14
15
16
17
18
19
20
21
8
9
10
11
12
13
14
15
16
17
18
19
20
7
8
9
10
11
12
13
14
15
16
17
18
19
6
7
8
9
10
11
12
13
14
15
16
17
18
5
6
7
8
9
10
11
12
13
14
15
16
17
4
5
6
7
8
9
10
11
12
13
14
15
16
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
1
2
3
4
5
6
7
8
9
10
11
12
13
+
1
2
3
4
5
6
7
8
9
10
11
12
3+9=12
在乘法表上把积是12的方格圈起来,可连成一条曲线.
12
12
24
36
48
60
72
84
96
108
120
132
144
11
11
22
33
44
55
66
77
88
99
110
121
132
10
10
20
30
40
50
60
70
80
90
100
110
120
9
19
18
27
36
45
54
63
72
81
90
99
108
8
8
16
24
32
40
48
56
64
72
80
88
96
7
7
14
21
28
35
42
49
56
63
70
77
84
6
6
12
18
24
30
36
42
48
54
60
66
72
5
5
10
15
20
25
30
35
40
45
50
55
60
4
4
8
12
16
20
24
28
32
36
40
44
48
3
3
6
9
12
15
18
21
24
27
30
33
36
2
2
4
6
8
10
12
14
16
18
20
22
24
1
1
2
3
4
5
6
7
8
9
10
11
12
+
1
2
3
4
5
6
7
8
9
10
11
12
3×4=12
王叔叔要去游长城,不同的交通工具所需时间如下,请把表填完整。
时间/时
10
40
80
12
3
1.5
…
…
速度/千米
自行车
公共汽车
小汽车
速度是10,时间是12;
速度是40,时间是3;
速度是80,时间是1.5;
速度和所需时间是两种相关联的量,所需时间是随着速度的变化而变化的。
速度扩大,所需时间缩小。
速度缩小,所需时间扩大。
对应的速度和所需时间的积总是一定的:
10×12=120
40×3=120
80×1.5=120
(一定)
速度×时间=路程
有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
150
200
300
(1)表中有哪两种量?
表中有每杯的果汁量和分的杯数两种量
(2)分的杯数是怎样随着每杯的果汁量变化的?
每杯的果汁量扩大,分的杯数反而缩小;
每杯的果汁量缩小,分的杯数反而扩大;
每杯的果汁量和分的杯数的积是一定的
(3)它们的关系是什么?
每杯的果汁量× 分的杯数= 果汁总量(一定)
有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
150
200
300
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。 XY=K(一定)
(一定)
速度×时间=路程
每杯的果汁量× 分的杯数= 果汁总量(一定)
判定方法:
判定两个量是不是成反比例,主
要是看它们的积是不是一定的。
在加法表上把和是12的方格圈起来,可连成一条直线.
12
13
14
15
16
17
18
19
20
21
22
23
24
11
12
13
14
15
16
17
18
19
20
21
22
23
10
11
12
13
14
15
16
17
18
19
20
21
22
9
10
11
12
13
14
15
16
17
18
19
20
21
8
9
10
11
12
13
14
15
16
17
18
19
20
7
8
9
10
11
12
13
14
15
16
17
18
19
6
7
8
9
10
11
12
13
14
15
16
17
18
5
6
7
8
9
10
11
12
13
14
15
16
17
4
5
6
7
8
9
10
11
12
13
14
15
16
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
1
2
3
4
5
6
7
8
9
10
11
12
13
+
1
2
3
4
5
6
7
8
9
10
11
12
3+9=12
在乘法表上把积是12的方格圈起来,可连成一条曲线.
12
12
24
36
48
60
72
84
96
108
120
132
144
11
11
22
33
44
55
66
77
88
99
110
121
132
10
10
20
30
40
50
60
70
80
90
100
110
120
9
19
18
27
36
45
54
63
72
81
90
99
108
8
8
16
24
32
40
48
56
64
72
80
88
96
7
7
14
21
28
35
42
49
56
63
70
77
84
6
6
12
18
24
30
36
42
48
54
60
66
72
5
5
10
15
20
25
30
35
40
45
50
55
60
4
4
8
12
16
20
24
28
32
36
40
44
48
3
3
6
9
12
15
18
21
24
27
30
33
36
2
2
4
6
8
10
12
14
16
18
20
22
24
1
1
2
3
4
5
6
7
8
9
10
11
12
+
1
2
3
4
5
6
7
8
9
10
11
12
3×4=12
判断下面每题中的两种量是不是成反比例,并说明理由。
煤的总量一定,每天的烧煤量和能够烧的天数。
张伯伯骑自行车从家到县城,
骑自行车的速度和所需的时间。
判断下面每题中的两种量是不是成反比例,并说明理由。
生产电视机的总台数一定,每天生产的台数和所用的天数。
判断下面每题中的两种量是不是成反比例,并说明理由。
长方形的面积一定,它的长和宽。
判断下面每题中的两种量是不是成反比例,并说明理由。
铺地面积一定,方砖边长与所需块数。
判断下面每题中的两种量是不是成反比例,并说明理由。
谢 谢 !
