鲁教版(五四制)七年级下册数学 第八章 回顾与思考 课件(共27张)
文档属性
| 名称 | 鲁教版(五四制)七年级下册数学 第八章 回顾与思考 课件(共27张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 00:00:00 | ||
图片预览








文档简介
创境引入
创境引入
如图,填空
内错角相等,两直线平行
④∵ AC∥DF (已知)
∴∠3=∠D ( )
⑤∵∠B+∠4=180° (已知)
∴ AB∥DE ( )
⑥∵DF∥AC (已知)
∴ ∠D+∠5=180° ( )
同位角相等,两直线平行
两直线平行 ,同位角相等
两直线平行 ,内错角相等
同旁内角互补,两直线平行
两直线平行,同旁内角互补
①∵ ∠B=∠1 (已知)
∴ AB∥DE
( )
②∵ DF∥AC (已知)
∴ ∠2=∠F ( )
③∵ ∠A=∠3 (已知)
∴ AB∥DE ( )
A
B
D
E
C
F
1
3
2
5
4
平行线的判定方法
平行线的性质定理
条件
结论
条件
结论
同位角相等
内错角相等
同旁内角互补
两直线平行
两直线平行
同位角相等
内错角相等
同旁内角互补
问题:平行线的判定定理与平行线的性质定理的区别与联系?
(平行于同一条直线的两条直线互相平行)
a
b
c
∵ a ∥ b (已知)
又∵ a ∥ c(已知)
∴ b ∥c
“玩” 出学问
数学大师陈省身被国际数学界尊称为“微分几何之父”。
在2002年北京国际数学大会上为青少年题词“数学好玩”。
“玩” 出学问
1.小明是个爱动脑筋的学生,他将直尺和含60°的三角板按如图所示叠放,当∠1=40 °时,你能帮他求出∠2, ∠3的度数吗?
1
2
3
A
B
C
F
D
E
4
G
一分钟看图考虑,想好的同学要
快速举手,10秒倒计时后抢答.
“玩” 出学问
10
9
8
7
6
5
4
3
2
1
0
1
2
3
A
B
C
F
D
E
4
G
1.小明是个爱动脑筋的学生,他将直尺和含60°的三角板按如图所示叠放,当∠1=40 °时,你能帮他求出∠2, ∠3的度数吗?
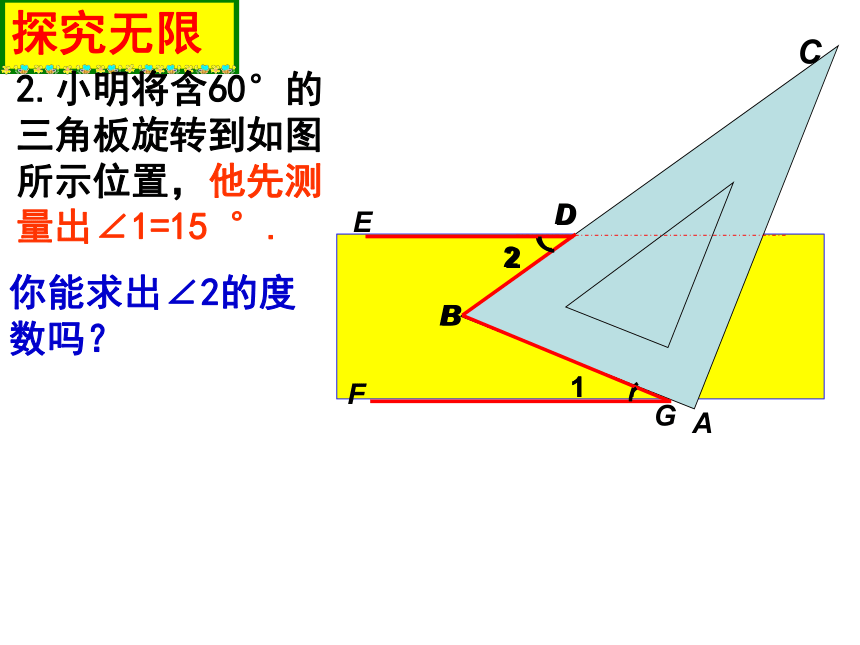
探究无限
2
C
D
你能求出∠2的度数吗?
2.小明将含60°的
三角板旋转到如图
所示位置,他先测
量出∠1=15 °.
A
E
F
1
2
B
D
G
1
B
探究无限
1
2
B
D
G
E
F
2.已知:如图,DE∥GF,∠B=60°,∠1=15°
问题1:求∠2的度数.
探究无限
问题2:∠B 与∠1,∠2有着怎样的数量关系?
2.已知:如图,DE∥GF,∠B=60°,∠1=15°
问题1:求∠2的度数.
3
4
3
3
4
探究无限
在上图中,如果只有DE∥GF的条件,
∠B 与∠1,∠2还有这样的数量关系吗?
3
4
3
4
3
探究无限
数学思想
数学方法
作平行线
构造
两组内错角
作截线
三角形
转化思想
构造
转化思想
3
4
3
3
4
类比探索
2.小明继续旋转三角板到如图所示位置,他发现∠B ,∠1 ,∠2之间依然有着奇妙的数量关系.聪明的你能猜想出来吗?
C
A
1
2
B
D
E
F
G
1
2
B
D
E
F
G
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
想
化
比
猜
转
类
1
2
B
D
E
F
G
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
1
2
B
D
E
F
G
3
4
想
化
比
猜
转
类
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
1
2
B
D
E
F
G
想
化
比
猜
转
类
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
1
2
B
D
E
F
G
3
想
化
比
猜
转
类
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
1
2
B
D
E
F
G
H
3
想
化
比
猜
转
类
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
1
2
D
E
F
G
H
3
4
B
想
化
比
猜
转
类
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
1
2
B
D
E
F
G
H
3
4
5
想
化
比
猜
转
类
类比探索
A
C
2
B
F
1
G
变化无穷
C
2
B
D
E
F
1
G
2
D
1
D
E
达标检测
DE∥GF
∠B =∠1+∠2
∠B =∠1+∠2
DE∥GF
?
1.已知:如图,∠B =∠1+∠2
求证:DE∥GF
2.已知:如图, ∠B +∠1 +∠2= 360°
求证:DE∥GF
1
2
B
D
E
F
G
反思升华
责任达成(必做题)
分层作业
1.已 知:如图1, ED ∥ GF,∠B ,∠1,∠2的数量关系为___________
2.已 知:如图2, ED ∥ GF,探究∠B 与∠1,∠2的数量关系并证明.
图1
图2
已 知:如图,直线AB∥CD,直线EF与两直线AB、CD分别相交于点G ,H ,GM , HN分别是∠EGB ,∠EHD 的角平分线, 试探究直线GM与HN的关系。
E
F
B
D
C
A
G
H
M
N
追求卓越(选做题)
创境引入
如图,填空
内错角相等,两直线平行
④∵ AC∥DF (已知)
∴∠3=∠D ( )
⑤∵∠B+∠4=180° (已知)
∴ AB∥DE ( )
⑥∵DF∥AC (已知)
∴ ∠D+∠5=180° ( )
同位角相等,两直线平行
两直线平行 ,同位角相等
两直线平行 ,内错角相等
同旁内角互补,两直线平行
两直线平行,同旁内角互补
①∵ ∠B=∠1 (已知)
∴ AB∥DE
( )
②∵ DF∥AC (已知)
∴ ∠2=∠F ( )
③∵ ∠A=∠3 (已知)
∴ AB∥DE ( )
A
B
D
E
C
F
1
3
2
5
4
平行线的判定方法
平行线的性质定理
条件
结论
条件
结论
同位角相等
内错角相等
同旁内角互补
两直线平行
两直线平行
同位角相等
内错角相等
同旁内角互补
问题:平行线的判定定理与平行线的性质定理的区别与联系?
(平行于同一条直线的两条直线互相平行)
a
b
c
∵ a ∥ b (已知)
又∵ a ∥ c(已知)
∴ b ∥c
“玩” 出学问
数学大师陈省身被国际数学界尊称为“微分几何之父”。
在2002年北京国际数学大会上为青少年题词“数学好玩”。
“玩” 出学问
1.小明是个爱动脑筋的学生,他将直尺和含60°的三角板按如图所示叠放,当∠1=40 °时,你能帮他求出∠2, ∠3的度数吗?
1
2
3
A
B
C
F
D
E
4
G
一分钟看图考虑,想好的同学要
快速举手,10秒倒计时后抢答.
“玩” 出学问
10
9
8
7
6
5
4
3
2
1
0
1
2
3
A
B
C
F
D
E
4
G
1.小明是个爱动脑筋的学生,他将直尺和含60°的三角板按如图所示叠放,当∠1=40 °时,你能帮他求出∠2, ∠3的度数吗?
探究无限
2
C
D
你能求出∠2的度数吗?
2.小明将含60°的
三角板旋转到如图
所示位置,他先测
量出∠1=15 °.
A
E
F
1
2
B
D
G
1
B
探究无限
1
2
B
D
G
E
F
2.已知:如图,DE∥GF,∠B=60°,∠1=15°
问题1:求∠2的度数.
探究无限
问题2:∠B 与∠1,∠2有着怎样的数量关系?
2.已知:如图,DE∥GF,∠B=60°,∠1=15°
问题1:求∠2的度数.
3
4
3
3
4
探究无限
在上图中,如果只有DE∥GF的条件,
∠B 与∠1,∠2还有这样的数量关系吗?
3
4
3
4
3
探究无限
数学思想
数学方法
作平行线
构造
两组内错角
作截线
三角形
转化思想
构造
转化思想
3
4
3
3
4
类比探索
2.小明继续旋转三角板到如图所示位置,他发现∠B ,∠1 ,∠2之间依然有着奇妙的数量关系.聪明的你能猜想出来吗?
C
A
1
2
B
D
E
F
G
1
2
B
D
E
F
G
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
想
化
比
猜
转
类
1
2
B
D
E
F
G
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
1
2
B
D
E
F
G
3
4
想
化
比
猜
转
类
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
1
2
B
D
E
F
G
想
化
比
猜
转
类
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
1
2
B
D
E
F
G
3
想
化
比
猜
转
类
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
1
2
B
D
E
F
G
H
3
想
化
比
猜
转
类
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
1
2
D
E
F
G
H
3
4
B
想
化
比
猜
转
类
类比探索
2. 已知:如图,直线 ED ∥ GF,
猜想:∠B +∠1 +∠2=
360°
1
2
B
D
E
F
G
H
3
4
5
想
化
比
猜
转
类
类比探索
A
C
2
B
F
1
G
变化无穷
C
2
B
D
E
F
1
G
2
D
1
D
E
达标检测
DE∥GF
∠B =∠1+∠2
∠B =∠1+∠2
DE∥GF
?
1.已知:如图,∠B =∠1+∠2
求证:DE∥GF
2.已知:如图, ∠B +∠1 +∠2= 360°
求证:DE∥GF
1
2
B
D
E
F
G
反思升华
责任达成(必做题)
分层作业
1.已 知:如图1, ED ∥ GF,∠B ,∠1,∠2的数量关系为___________
2.已 知:如图2, ED ∥ GF,探究∠B 与∠1,∠2的数量关系并证明.
图1
图2
已 知:如图,直线AB∥CD,直线EF与两直线AB、CD分别相交于点G ,H ,GM , HN分别是∠EGB ,∠EHD 的角平分线, 试探究直线GM与HN的关系。
E
F
B
D
C
A
G
H
M
N
追求卓越(选做题)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
