鲁教版(五四制)八年级下册数学 第八章 一元二次方程回顾与总结 课件(23张)
文档属性
| 名称 | 鲁教版(五四制)八年级下册数学 第八章 一元二次方程回顾与总结 课件(23张) | 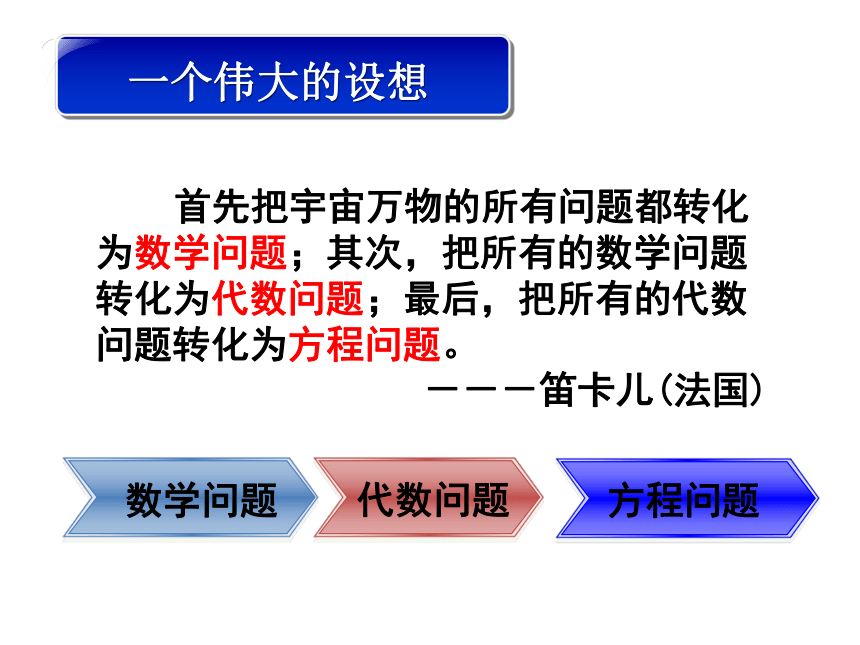 | |
| 格式 | ppt | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 22:43:09 | ||
图片预览







文档简介
一个伟大的设想
数学问题
代数问题
方程问题
首先把宇宙万物的所有问题都转化为数学问题;其次,把所有的数学问题转化为代数问题;最后,把所有的代数问题转化为方程问题。
---笛卡儿(法国)
鲁教五?四学制2011课标版
八年级下册第八章
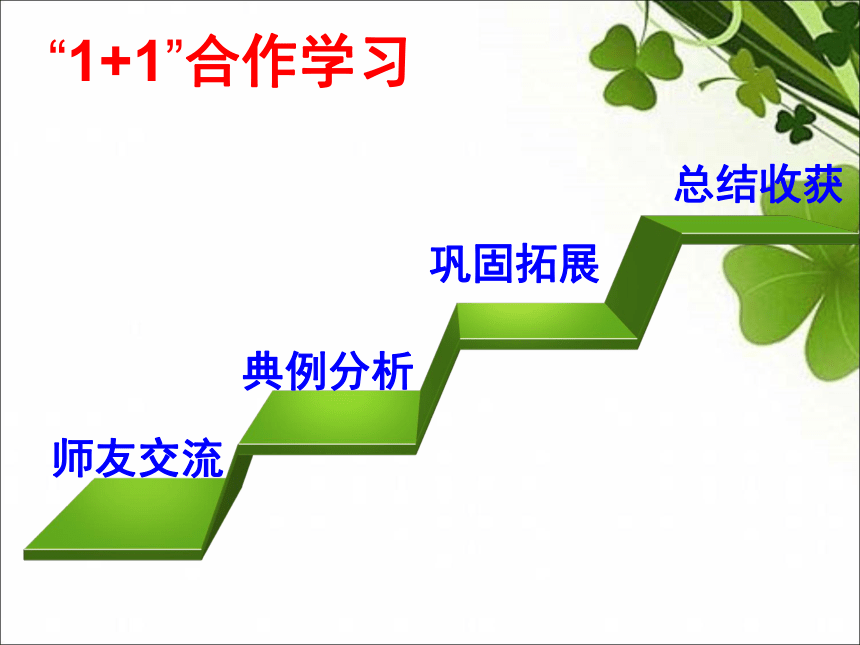
典例分析
师友交流
总结收获
巩固拓展
“1+1”合作学习
师友交流
1.课前自主纠错后还有什么疑问.
2.学师帮学友解决疑问.
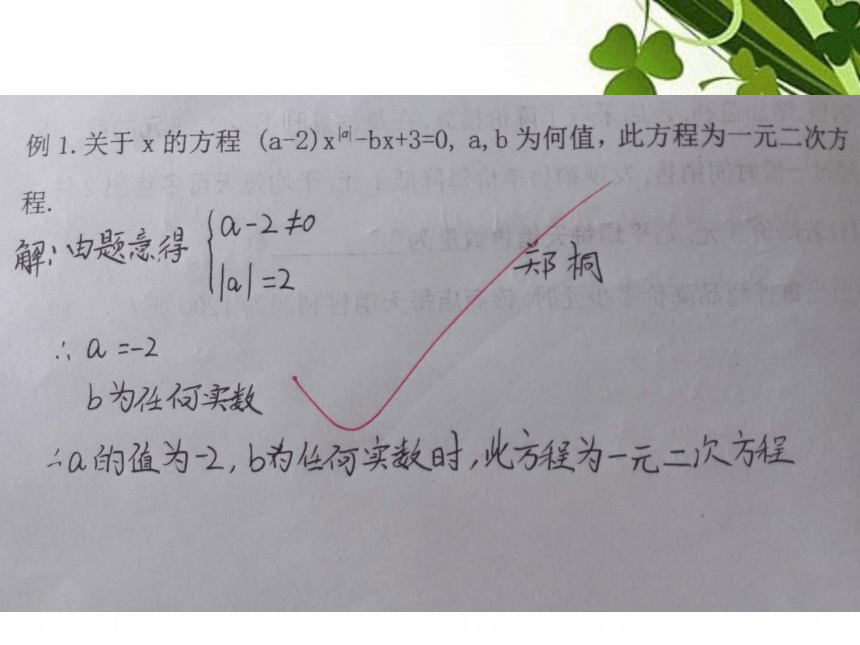
例1.关于x的方程 (a-2)x|a| -bx+3=0,
a,b为何值,此方程为一元二次方程.
例2.解方程x2+12x-15=0
例3.已知关于x的方程x2 +(m+1)x+(m-2)2=0有两个相等的实数根。
(1)求m的值; (2)求出此时方程的根。
例4.某商场将进价为30元的台灯以40元售出,平均每月能售出600个。调查发现,这种台灯的售价每上涨1元,其销售量就减少10个。应涨价多少元才能实现平均每月10000元的销售利润?
例1.关于x的方程 (a-2)x|a| -bx+3=0,
a,b为何值,此方程为一元二次方程.
典例分析
例2.解方程x2+12x-15=0
典例分析
巩固拓展
1.用配方法证明:
无论x取何实数,代数式2x2-8x+18的值不小于10.
例3.已知关于x的方程x2 +(m+1)x+(m-2)2=0有两个相等的实数根。
(1)求m的值;
(2)求出此时方程的根。
典例分析
2.已知关于x的方程x2+ax+a-2=0.
(1)当该方程的一个根为1时,求a的值 及该方程的另一根;
(2)求证:不论a取何实数,该方程都 有两个不相等的实数根.
巩固拓展
例4.某商场将进价为30元的台灯以40元售出,平均每月能售出600个。调查发现,这种台灯的售价每上涨1元,其销售量就减少10个。应涨价多少元才能实现平均每月10000元的销售利润?
典例分析
巩固拓展
3.一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为 件;?
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?
总结收获
用公式法解一元二次方程的一般步骤:
4、代入求根公式 :
3、求出 的值.
1、把方程化成一般形式
5、写出方程的解:
特别注意:若 则方程无解
2、写出 的值.
我们把b2-4ac叫做一元二次方程ax2+bx+c=0(a ≠ 0)的根的判别式,通常用希腊字母“△ ”表示.
b2-4ac>0 有两个不相等的实数根;
b2-4ac=0 有两个相等的实数根;
b2-4ac<0 方程没有实数根.
给我最大快乐的,不是已懂的知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登。
---- 高斯(法国)
数学问题
代数问题
方程问题
首先把宇宙万物的所有问题都转化为数学问题;其次,把所有的数学问题转化为代数问题;最后,把所有的代数问题转化为方程问题。
---笛卡儿(法国)
鲁教五?四学制2011课标版
八年级下册第八章
典例分析
师友交流
总结收获
巩固拓展
“1+1”合作学习
师友交流
1.课前自主纠错后还有什么疑问.
2.学师帮学友解决疑问.
例1.关于x的方程 (a-2)x|a| -bx+3=0,
a,b为何值,此方程为一元二次方程.
例2.解方程x2+12x-15=0
例3.已知关于x的方程x2 +(m+1)x+(m-2)2=0有两个相等的实数根。
(1)求m的值; (2)求出此时方程的根。
例4.某商场将进价为30元的台灯以40元售出,平均每月能售出600个。调查发现,这种台灯的售价每上涨1元,其销售量就减少10个。应涨价多少元才能实现平均每月10000元的销售利润?
例1.关于x的方程 (a-2)x|a| -bx+3=0,
a,b为何值,此方程为一元二次方程.
典例分析
例2.解方程x2+12x-15=0
典例分析
巩固拓展
1.用配方法证明:
无论x取何实数,代数式2x2-8x+18的值不小于10.
例3.已知关于x的方程x2 +(m+1)x+(m-2)2=0有两个相等的实数根。
(1)求m的值;
(2)求出此时方程的根。
典例分析
2.已知关于x的方程x2+ax+a-2=0.
(1)当该方程的一个根为1时,求a的值 及该方程的另一根;
(2)求证:不论a取何实数,该方程都 有两个不相等的实数根.
巩固拓展
例4.某商场将进价为30元的台灯以40元售出,平均每月能售出600个。调查发现,这种台灯的售价每上涨1元,其销售量就减少10个。应涨价多少元才能实现平均每月10000元的销售利润?
典例分析
巩固拓展
3.一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为 件;?
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?
总结收获
用公式法解一元二次方程的一般步骤:
4、代入求根公式 :
3、求出 的值.
1、把方程化成一般形式
5、写出方程的解:
特别注意:若 则方程无解
2、写出 的值.
我们把b2-4ac叫做一元二次方程ax2+bx+c=0(a ≠ 0)的根的判别式,通常用希腊字母“△ ”表示.
b2-4ac>0 有两个不相等的实数根;
b2-4ac=0 有两个相等的实数根;
b2-4ac<0 方程没有实数根.
给我最大快乐的,不是已懂的知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登。
---- 高斯(法国)
