人教版八年级下册数学18.1《平行四边形》同步专项提升 (Word版 含答案)
文档属性
| 名称 | 人教版八年级下册数学18.1《平行四边形》同步专项提升 (Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 642.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 12:23:45 | ||
图片预览



文档简介
人教版八年级下册数学18.1《平行四边形》同步专项提升
一.选择题
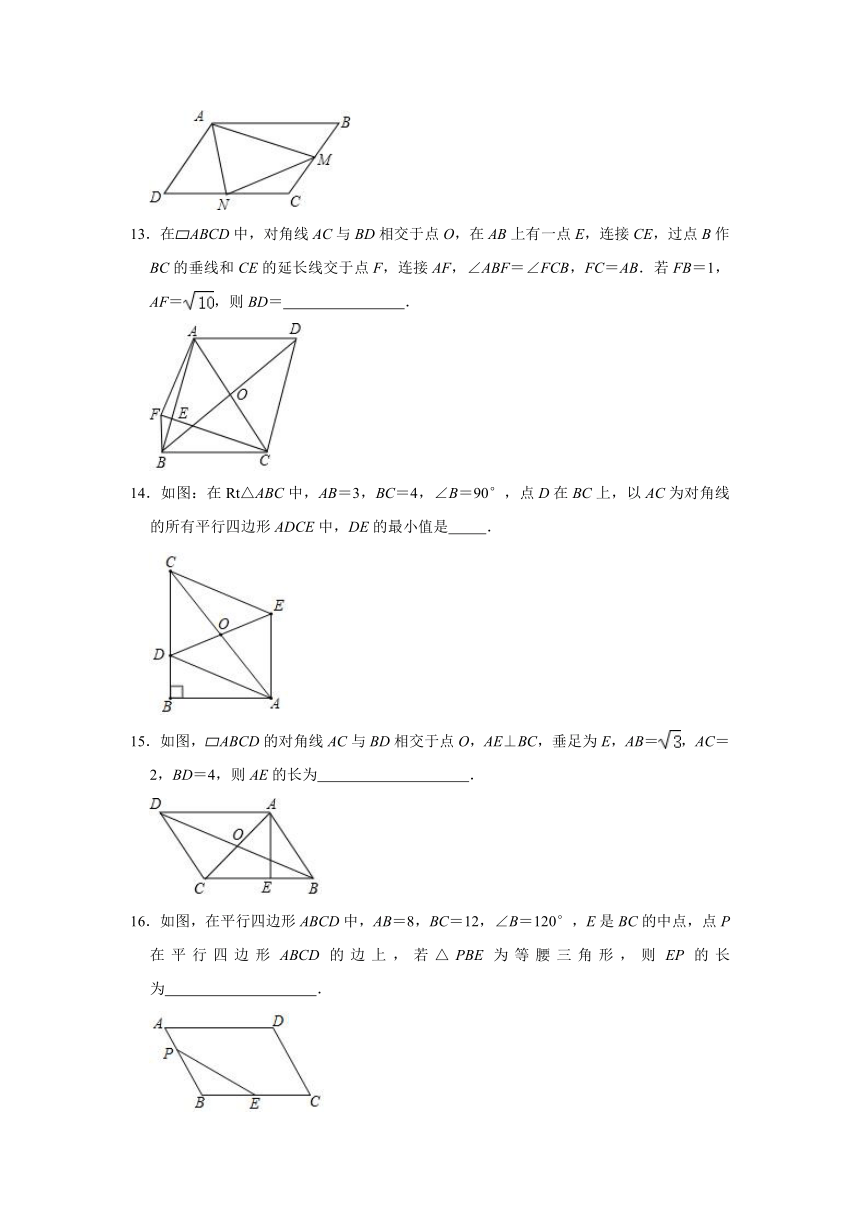
1.如图,在?ABCD中,AE⊥BC,垂足为E,AF⊥CD,垂足为F.若AE:AF=2:3,?ABCD的周长为10,则AB的长为( )
A.2 B.2.5 C.3 D.3.5
2.如图,在平行四边形ABCD中,,AD=4,AC⊥BC,则△DBC比△ABC的周长长( )
A.2 B.4 C.5 D.
3.如图,在平行四边形ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB的长是( )
A.4 B.2 C.2 D.2
4.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB?AC;③OB=AB;④OE=BC.其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,在平行四边形ABCD中,点A、B、C的坐标分别为(2,0)、(0,1)、(1,2),则平行四边形ABCD的周长为( )
A. B.6 C.8 D.10
6.如图,在△ABC中,∠ACB=60°,∠CAB=45°,BC=4,点D为AB边上一个动点,连接CD,以DA、DC为一组邻边作平行四边形ADCE,则对角线DE的最小值是( )
A.+ B.1+ C.4 D.2+2
7.如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE,CF和EF,则下列结论,一定成立的个数是( )
①△CDF≌△EBC;②△CEF是等边三角形;③∠CDF=∠EAF;④CE∥DF
A.1 B.2 C.3 D.4
8.在平行四边形ABCD中,AB≠BC,F是BC上一点,AE平分∠FAD,且E是CD的中点,则下列结论:①AE⊥EF,②AF=CF+CD,③AF=CF+AD,④AB=BF,其中正确的是( )
A.②④ B.①② C.①③ D.①②④
9.如图,在平行四边形ABCD中,点E是BC的中点,作EF⊥AE交CD于F,若∠BAE=45°,AE=4,下列结论:①∠EAF=45°,②AF=AB+CF,③CD=2CF,④S△AEF=8中正确的是( )
A.①②④ B.①③④ C.①②③ D.②③④
10.如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边三角形△ACD和△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④其中,正确的是( )
A.只有①② B.只有①②③ C.只有③④ D.①②③④
二.填空题
11.已知平面直角坐标系上有三个点,点A(2,0),B(5,2),C(3,4),以点A,点B,点C为顶点画平行四边形,则第四个顶点D的坐标为_ .
12.如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是 .
13.在?ABCD中,对角线AC与BD相交于点O,在AB上有一点E,连接CE,过点B作BC的垂线和CE的延长线交于点F,连接AF,∠ABF=∠FCB,FC=AB.若FB=1,AF=,则BD= .
14.如图:在Rt△ABC中,AB=3,BC=4,∠B=90°,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是 .
15.如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=,AC=2,BD=4,则AE的长为 .
16.如图,在平行四边形ABCD中,AB=8,BC=12,∠B=120°,E是BC的中点,点P在平行四边形ABCD的边上,若△PBE为等腰三角形,则EP的长为 .
17.在平面直角坐标系中,已知三点O(0,0),A(1,﹣2),B(3,1),若以A、B、C、O为顶点的四边形是平行四边形,则点C的坐标为 .
18.如图,在直角坐标系中,?ABCO的顶点B的坐标为(6,m),C的坐标为(2,n)则点A的坐标为 .(用字母m,n表示)
19.如图,已知平行四边形ABCD,DE⊥CD,CE⊥BC,CE=AD,F为BC上一点,连接DF,且点A在BF的垂直平分线上,若DE=1,DF=5,则AD的长为 .
20.如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF= .
三.解答题
21.如图,?ABCD中,CG⊥AB于点G,∠ABF=45°,F在CD上,BF交CG于点E,连接AE,AE⊥AD.
(1)若BG=1,BC=,求EF的长度;
(2)求证:AB﹣BE=CF.
22.如图,在平行四边形ABCD中,E为AD上一点,连接EB并延长到点F,使BF=BE,连接EC并延长到点M,使CM=EC,连接FM,N为FM的中点,连接AF、DN
(1)求证:四边形AFND为平行四边形;
(2)在不添加任何辅助线的情况下,直接写出图中长度为FM的一半的所有线段.
23.如图,在平行四边形ABCD中,点E是AB边上一点,CE=AB,DF⊥BC,垂足为点F,交CE于点G,连接DE,EF.
(1)求证:∠AED=90°﹣∠DCE;
(2)若点E是AB边的中点,求证:∠EFB=∠DEF.
24.若平面内两点P1(x1,y2),P2(x2,y2),其两点间的距离P1P2=.例如:已知A(3,1),B(5,2),则这两点间的距离AB=.已知A(3,1),B(5,2),C(4,4).
(1)聪明的你能判定△ABC的形状吗?并说明理由.
(2)若以点A、B、C、D为顶点的四边形是平行四边形时,请直接写出点D的坐标.
25.如图,在四边形ABCD中,AD∥BC,AD=BC=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF.
(1)若∠ADC=80°,求∠ECF;
(2)求证:∠ECF=∠CEF.
26.已知:平行四边形ABCD中,∠ABC=45°,对角线AC⊥CD.
(1)如图1,若AD=6,求平行四边形ABCD的面积.
(2)如图2,连接BD交AC于O点,过点A作AE⊥BD于E,连接EC.求证:ED=AE+EC.
27.已知,在平行四边形ABCD中,DE⊥BC于E,点F是DE上一点,满足BA⊥BF,连接CF.
(1)如图1,连接AF,若BF=2,DC=4,∠DAF=30°,求AD;
(2)如图2,延长CF,交AD于点G,若BA=BF,求证:AG=2EF.
28.已知:平行四边形ABCD中,BD=CD,且∠ABD=45°,过D作DF⊥AB于F,点E是AD的中点,连接BE交DF于点P,点G是AB的中点,过B作BH⊥BD交PG的延长线于H.
(1)若AB=2,求DP的长;
(2)求证:DP=BH.
29.如图,在?ABCD中,∠B=45°,过点C作CE⊥AD于点,连接AC,过点D作DF⊥AC于点F,交CE于点G,连接EF.
(1)若DG=8,求对角线AC的长;
(2)求证:AF+FG=EF.
30.如图,已知平行四边形ABCD中,BC=2AB,点E是BC的中点,∠ABC=120°,点P为CD边上任意一点,连接BP,点G为BP上一点,连接AG,EG,CG,使∠AGB=∠EGB,点F在AG上,且GF=GE,连接EF,DF
(1)若AB=5,DP=3,求线段BP的长度;
(2)求证:CG=DF.
2020年人教版八下数学《18.1 平行四边形》专项提升【1】
参考答案与试题解析
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴BC+CD=10÷2=5,
根据平行四边形的面积公式,得BC:CD=AF:AE=3:2.
∴BC=3,CD=2,
∴AB=CD=2,
故选:A.
2.解:在?ABCD中,∵AB=CD=2cm,AD=BC=4cm,AO=CO,BO=DO,
∵AC⊥BC,
∴AC==6cm,
∴OC=3cm,
∴BO==5cm,
∴BD=10cm,
∴△DBC的周长﹣△ABC的周长=BC+CD+BD﹣(AB+BC+AC)=BD﹣AC=10﹣6=4cm,
故选:B.
3.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴CE=2AB,
∵∠BCD=∠BAD=120°,
∴∠ECF=60°,
∵EF⊥BC,
∴∠CEF=30°,
∴CE=2CF=4,
∴AB=2.
故选:B.
4.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
∴AE=BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S?ABCD=AB?AC,故②正确,
∵AB=BC,OB=BD,
∵BD>BC,
∴AB≠OB,故③错误;
或∵AC⊥AB,
∴AB<OB,故③错误;
∵∠CAD=30°,∠AEB=60°,AD∥BC,
∴∠EAC=∠ACE=30°,
∴AE=CE,
∴BE=CE,
∵OA=OC,
∴OE=AB=BC,故④正确.
故选:C.
5.解:∵点A、B的坐标分别为(2,0)、(0,1),
∴OA=2,OB=1,
∴AB==,
过C作CE⊥y轴于E,如图所示:
∵点C的坐标为(1,2),
∴CE=1,OE=2,
∴BE=1,
∴BC==,
∴AB+BC=+,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴平行四边形ABCD的周长=2(AB+BC)=2+2
故选:A.
6.解:设DE交AC于O,作BF⊥AC于F,如图所示:
则∠BFC=∠BFA=90°,
∵∠ACB=60°,∠CAB=45°,
∴∠CBF=30°,∠ABF=90°﹣45°=45°=∠CAB,
∴CF=BC=2,AF=BF=CF=2,
∴AC=CF+AF=2+2,
∵四边形ADCE是平行四边形,
∴AO=CO=AC=1+,DO=EO,
∴当OD⊥AB时,DO的值最小,即DE的值最小,
则△AOD是等腰直角三角形,
∴OD=AO=,
∴DE=2OD=+;
故选:A.
7.解:在?ABCD中,∠ADC=∠ABC,AD=BC,CD=AB,
∵△ABE、△ADF都是等边三角形,
∴AD=DF,AB=EB,∠DFA=∠ADF=∠ABE=60°,
∴DF=BC,CD=BE,
∴∠CDF=∠ADC﹣60°,
∠EBC=∠ABC﹣60°,
∴∠CDF=∠EBC,
在△CDF和△EBC中,,
∴△CDF≌△EBC(SAS),故①正确;
在?ABCD中,设AE交CD于O,AE交DF于K,如图:
∵AB∥CD,
∴∠DOA=∠OAB=60°,
∴∠DOA=∠DFO,
∵∠OKD=∠AKF,
∴∠ODF=∠OAF,
故③正确;
在△CDF和△EAF中,,
∴△CDF≌△EAF(SAS),
∴EF=CF,
∵△CDF≌△EBC,
∴CE=CF,
∴EC=CF=EF,
∴△ECF是等边三角形,故②正确;
则∠CFE=60°,
若CE∥DF时,
则∠DFE=∠CEF=60°,
∵∠DFA=60°=∠CFE,
∴∠CFE+∠DFE+∠DFA=180°,
则C、F、A三点共线
已知中没有给出C、F、A三点共线,故④错误;
综上所述,正确的结论有①②③.
故选:C.
8.解:延长AD,交FE的延长线于点M,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠M=∠EFC,
∵E是CD的中点,
∴DE=CE,
在△DEM和△CEF中,
,
∴△DEM≌△CEF(AAS),
∴EM=EF,
过点E作ET⊥AM于T,ER⊥AF于R.
∵AE平分∠FAD,
∴ET=ER,
∵EM=EF,∠ETM=∠ERF=90°,
∴Rt△ETM≌Rt△ERF(HL),
∴∠M=∠AFM,
∴AM=AF,
即AF=AD+DM=CF+AD;故③,①正确,②错误.
∵AF不一定是∠BAD的角平分线,
∴AB不一定等于BF,故④错误.
故选:C.
9.解:作EM∥AB交AF于M,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴AB∥EM∥CD,
∴AM:FM=BE:CE,∠AEM=∠BAE=45°,
∵点E是BC的中点,
∴BE=CE,
∴AM=FM,
∴EM是梯形ABCF的中位线,
∴AB+CF=2EM,
∵EF⊥AE,
∴∠AEF=90°,
∴EM=AF=AM=FM,
∴∠EAF=∠AEM=45°,AF=AB+CF,①②正确;
∴△AEF是等腰直角三角形,
∴FE=AE=4,
∴S△AEF═AE×FE=×4×4=8,④正确;
∵∠BAF=∠BAE+∠EAF=90°,
∴AF⊥AB,
∵AB∥CD,
∴AF⊥CD,
当AD=AC时,CF=DF,则CD=2CF,③不正确;
故选:A.
10.解:∵∠ACB=90°,∠ABC=30°,
∴∠BAC=60°,AC=AB,
∵△ACD是等边三角形,
∴∠ACD=60°,
∴∠ACD=∠BAC,
∴CD∥AB,
∵F为AB的中点,
∴BF=AB,
∴BF∥CD,CD=BF,
∴四边形BCDF为平行四边形,②正确;
∵四边形BCDF为平行四边形,
∴DF∥BC,又∠ACB=90°,
∴AC⊥DF,①正确;
∵DA=CA,DF=BC,AB=BE,BC+AC>AB
∴DA+DF>BE,③错误;
设AC=x,则AB=2x,
S△ACD=x2,S△ACB=x2,S△ABE=x2,
==,④错误,
故选:A.
二.填空题
11.解:以AC为对角线,将AB向上平移2个单位,再向左平移2个单位,A点对应的位置为(0,2)就是第四个顶点D;
以AB为对角线,将BC向下平移4个单位,再向左平移1个单位,B点对应的位置为(4,﹣2)就是第四个顶点D′;
以BC为对角线,将AB向上平移4个单位,再向右平移1个单位,B点对应的位置为(6,6)就是第四个顶点D″;
∴第四个顶点D的坐标为:(0,2)或(6,6)或(4,﹣2),
故答案为:(0,2)或(6,6)或(4,﹣2).
12.解:延长DC和AM交于E,过点E作EH⊥AN于点H,如图.
∵四边形ABCD为平行四边形,
∴AB∥CE,
∴∠BAM=∠CEM,∠B=∠ECM.
∵M为BC的中点,
∴BM=CM.
在△ABM和△ECM中,
,
∴△ABM≌△ECM(AAS),
∴AB=CD=CE,AM=EM=4,
∵N为边DC的中点,
∴NE=3NC=AB,即AB=NE,
∵AN=3,AE=2AM=8,且∠MAN=60°,
∴∠AEH=30°,
∴AH=AE=4,
∴EH==4,
∴NH=AH﹣AN=4﹣3=1,
∴EN==7,
∴AB=×7=.
故答案为.
13.解:延长BF、DA交于点G,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠GAB=∠ABC,
∵BF⊥BC,
∴∠FBC=∠FBA+∠ABC=90°,
∴∠FBA+∠GAB=90°,
∴∠G=90°,
在△AGB和△FBC中,
∵,
∴△AGB≌△FBC(AAS),
∴AG=BF=1,BC=BG,
Rt△AGF中,∵AF=,
∴FG=,
∴BC=BG=AD=3+1=4,
∴GD=1+4=5,
Rt△DGB中,BD=,
故答案为:.
14.解:∵在Rt△ABC中,∠B=90°,
∴BC⊥AB.
∵四边形ADCE是平行四边形,
∴OD=OE,OA=OC.
∴当OD取最小值时,DE线段最短,此时OD⊥BC.
∴OD∥AB,
∴OD是△ABC的中位线,
∴OD=AB=1.5,
∴ED=2OD=3.
故答案为:3.
15.解:∵AC=2,BD=4,四边形ABCD是平行四边形,
∴AO=AC=1,BO=BD=2,
∵AB=,
∴AB2+AO2=BO2,
∴∠BAC=90°,
∵在Rt△BAC中,BC=,
S△BAC=×AB×AC=×BC×AE,
∴2=AE,
∴AE=,
故答案为:.
16.解:当P点在BA上,BP=BE=6,
作BH⊥PE于H,如图1,则PH=EH,
∵∠B=120°,
∴∠BPE=∠BEP=30°,
在Rt△BEH中,BH=BE=3,EH=BH=3,
∴PE=2EH=6;
当P点在AD上,BP=PE,
作BG⊥AD于G,PF⊥BE于F,如图2,则BF=EF=3,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∵∠ABC=120°,
∴∠A=60°,
在Rt△ABG中,AG=AB=4,BG=AG=4,
∴PF=4,
在Rt△PEF中,PE==;
当点P在CD上,如图3,EB=EP=6,
综上所述,PE的长为6或6或.
故答案为6或6或.
17.解:如图,观察图象可知,满足条件的点C的坐标为(2,3)或(﹣2,﹣3)或(4,﹣1)
故答案为(2,3)或(﹣2,﹣3)或(4,﹣1).
18.解:∵?ABCO的顶点B的坐标为(6,m),C的坐标为(2,n),OA∥BC,OA=BC,
∴B、C横坐标的差为6﹣2=4,纵坐标的差为m﹣n,
∵O(0,0),
∴则点A的坐标为(4,m﹣n);
故答案为:(4,m﹣n).
19.解:连接AF,AC,过点A作AH⊥CD于H,AH交EC于O,
设AD与CE交于G,
∵∠AGC=∠AHC=90°,∠AOG=∠COH,
∴∠DAH=∠ECD,
∵∠AHD=∠EDC=90°,AD=CE,
∴△ADH≌△CED(AAS),
∴DE=DH=1,AH=CD,
∵点A在BF的垂直平分线上,
∴AB=AF,
∴∠ABF=∠AFB,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∴∠ABF+∠BCD=180°,
∴∠BCD=∠AFC,
∵CF=CF,
∴△AFC≌△DCF(SAS),
∴DF=AC=5,
设CH=x,则AH=CD=x+1,
∵AH2+CH2=AC2,
∴(x+1)2+x2=52,
解得:x=3(负值舍去),
∴AH=4,
∴AD==,
故答案为:.
20.解:如图,延长AE,BC交于点G,
∵点E是CD的中点,
∴DE=CE,
∵平行四边形ABCD中,AD∥BC,
∴∠D=∠ECG,
又∵∠AED=∠GEC,
∴△ADE≌△GCE,
∴CG=AD=5,AE=GE,
又∵AE平分∠FAD,AD∥BC,
∴∠FAE=∠DAE=∠G=∠DAF=30°,
∴AF=GF=3+5=8,
又∵E是AG的中点,
∴FE⊥AG,
∴Rt△AEF中,EF=AF=4,
故答案为:4.
三.解答题
21.解:(1)∵CG⊥AB,BG=1,,
∴.
∵∠ABF=45°,
∴△BGE是等腰直角三角形,
∴EG=BG=1,
∴EC=CG﹣EG=3﹣1=2,
∵在平行四边形ABCD中,AB∥CD,∠ABF=45°,CG⊥AB,
∴∠CFE=∠ABF=45°,∠FCE=∠BGE=90°,
∴△ECF是等腰直角三角形,
∴EF==2;
(2)证明:过E作EH⊥BE交AB于H,
∵∠ABF=45°,∠BEH=90°,
∴△BEH是等腰直角三角形,
∴,BE=HE,
∴∠BHE=45°,
∴∠AHE=180°﹣∠BHE=180°﹣45°=135°,
由(1)知,△BGE和△ECF都是等腰直角三角形,
∴∠BEG=45°,CE=CF,
∴∠BEC=180°﹣∠BEG=180°﹣45°=135°,
∴∠AHE=∠CEB,
∵AE⊥AD,
∴∠DAE=90°,
∴∠BAD=∠DAE+∠EAB=90°+∠EAB,
由(1)知,∠FCE=90°,
∴∠BCD=∠FCE+∠BCG=90°+∠BCG,
∵在平行四边形ABCD中,∠BAD=∠BCD,
∴90°+∠EAB=90°+∠BCG,
∴∠EAB=∠BCG,
即∠EAH=∠BCE,
在△△EAH和△BCE中,
∴△EAH≌△BCE(AAS),
∴AH=CE=CF,
∴AB﹣BE=AB﹣BH=AH=CF,
即AB﹣BE=CF.
22.(1)证明:如图,∵EB=BF,EC=CM,
∴BC∥FM,BC=FM,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD∥FM,
∵N为FM的中点,
∴FN=FM,
∴AD=FN,
∴四边形AFND是平行四边形;
(2)解:∵四边形ABCD为平行四边形,
∴AD=BC,
∵BF=BE,CM=CE,
∴BC=FM,
∴AD=FM,
∵四边形AFND是平行四边形,
∴FN=AD=FM,
∴MN=FM,
∴长度为FH的一半的所有线段为:AD,BC,FN,MN.
23.证明:(1)∵CE=AB,AB=CD
∴CE=CD,
∴∠CDE=∠CED==90°﹣∠DCE,
∵CD∥AB
∴∠AED=∠CDE=90°﹣∠DCE;
(2)如图,延长DA,FE于点M,
∵四边形ABCD是平行四边形
∴AD∥BC,且DF⊥BC
∴DF⊥AD,∠M=∠EFB
∵∠M=∠EFB,AE=BE,∠AEM=∠FEB
∴△AEM≌△BEF(AAS)
∴ME=EF,且DF⊥DM
∴ME=DE=EF
∴∠M=∠MDE
∴∠DEF=∠M+∠MDE=2∠M
∴∠EFB=∠DEF
24.解:(1)能判定△ABC的形状,△ABC是等腰直角三角形;理由如下:
由题意得:AB=,BC==,AC==,
∴AB=BC,AB2+BC2=AC2,
∴△ABC是等腰直角三角形;
(2)如图所示:
当AB为对角线时,AD∥BC,
∵A(3,1),B(5,2),C(4,4),
∴把点B向下平移3个单位,再向左平移1个单位,得到点D,
∴点D的坐标为(4,﹣1);
当BC为对角线时,AB∥CD,
∵A(3,1),B(5,2),C(4,4),
∴把点B向上平移3个单位,再向右平移1个单位,得到点D',
∴点D'的坐标为(6,5);
当AC为对角线时,AD∥BC,
∵A(3,1),B(5,2),C(4,4),
∴把点A向上平移2个单位,再向左平移1个单位,得到点D'',
∴点D''的坐标为(2,3);
综上所述,点D的坐标为(4,﹣1)或(6,5)或(2,3).
25.解:(1)∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵F是AD的中点,
∴AF=FD,
∵在?ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF=(180°﹣80°)=50°,
∵CE⊥AB,
∴CE⊥CD,
∴∠DCE=90°,
∴∠ECF=90°﹣50°=40°;
(2)如图,延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=EM=FE,
∴∠ECF=∠CEF.
26.解:解法一:(1)∵∠ABC=45°,AC⊥CD,
∴△ACD是等腰直角三角形,
∵AD=6,
∴AC=CD=AD=3,
∴平行四边形ABCD的面积=33=18;
(2)过C作FC⊥EC交BD于F,
∵AE⊥BD,
∴∠AEO=∠CFO=90°,
∵∠AOE=∠COF,
∵平行四边形ABCD中,AO=CO,
∴△AOE≌△COF(AAS),
∴AE=CF,OE=OF,
∵∠ABC=45°,AC⊥CD,
∴△ACD是等腰直角三角形,
设AC=AB=2x,
∴AD=BC=2x,
∴AO=x,
∴BO=DO==x,
∵S△AOB=AB?AO=BO?AE,
∴AE===,
∴OE=OF==x,
∴EF=CF=x,
∴CE=EF=x,
∵DE==x,AE+EC=x+x=x,
∴ED=AE+EC;
解法二:过C作FC⊥EC交BD于F,∴∠FCE=90°,
∵AE⊥BD,
∴∠ACD=90°,
∴∠ECA+∠ACF=∠ACF+∠FCD,
∴∠ECA=∠FCD,
∵AE⊥BD,
∴∠AEB=90°,
∴∠ABD+∠BAE=∠BAE+∠EAC,
∴∠EAC=∠CDF,
∵AC⊥CD,∠ADC=∠ABC=45°,
∴△ACD是等腰直角三角形,
∴AC=CD,
∴△AEC≌△DFC(ASA),
∴AE=DF,EC=FC,
∴△ECF是等腰直角三角形,
∴EF=EC,
∴ED=DF+EF=AE+EC.
27.解:(1)∵四边形ABCD是平行四边形,
∴AB=CD=4,
∵BA⊥BF,
∴∠ABF=90°,
∵BF=2,
∴AF===10,
∵AD∥BC,DE⊥BC,
∴DE⊥AD,
∴∠ADF=90°,
∵∠DAF=30°,
∴AD=AF=5;
(2)∵在平行四边形ABCD中,AB=CD,AD∥BC,∠A=∠BCD,
又∵BA=BF,
∴BF=CD,∠A+∠ABC=180°,
∵BA⊥BF,
∴∠ABF=90°,
∴∠A+∠EBF=90°,
∵∠EDC+∠DCE=90°,
∴∠EBF=∠EDC,
∵DE⊥BC,
∴∠BEF=∠DEC=90°,
∴△BEF≌△DEC(AAS),
∴EF=CE,BE=DE,
∴∠EFC=∠ECF=45°,
∵∠DFG=∠CFE=45°,
∴△DFG是等腰直角三角形,
∴DG=DF,
设DG=DF=x,EF=CE=y,
∴BE=DE=x+y,
∴AD=BC=x+y+y=x+2y,
∴AG=AD﹣DG=x+2y﹣x=2y=2EF.
28.(1)解:如图,过P作PM⊥BD于M,
∵四边形ABCD是平行四边形,
∴CD=AB=2,
∵BD=CD,
∴AB=BD=2,
∵E是AD的中点,
∴∠DBE=∠ABE,
∵PF⊥AB,PM⊥BD,
∴PF=PM,
∵∠ABD=45°,
∴△BDF是等腰直角三角形,
∴DF=BF=,∠BDF=45°,
∴DM=PM,PD=DM,
在△BFP和△BMP中,
∵,
∴Rt△BFP≌Rt△BMP(HL),
∴BM=BF=,
∴DM=2﹣,
∴DP=DM=2﹣2;
(2)证明:连接AP,
∵∠DEP=∠PFB=90°,∠EPD=∠FPB,
∴∠EDP=∠FBP,
在△ADF和△PBF中,
∵,
∴△ADF≌△PBF(ASA),
∴PF=AF,
∴∠PAF=45°,
∵BD⊥BH,
∴∠DBH=90°,
∵∠DBF=45°,
∴∠HBG=90°﹣45°=45°,
∴∠PAF=∠HBG,
在△APG和△BHG中,
∵,
∴△APG≌△BHG(ASA),
∴BH=AP,
∵AB=BD,∠ABD=45°,
∴∠DAB=∠ADB=67.5°,
Rt△ADF中,∠ADP=∠DAP=22.5°,
∴AP=DP,
∴DP=BH.
29.解:(1)∵在?ABCD中,∠B=45°,
∴∠ADC=∠B=45°,
∵CE⊥AD,
∴△CDE是等腰直角三角形,
∴CE=DE,∠DEC=∠AEC=90°,
∵DF⊥AC,
∴∠CFD=∠DEC=90°,
∴∠DGE=∠CGF,
∴∠EDG=∠ECA,
∴△DEG≌△CEA(ASA),
∴AC=DG=8;
(2)过E作EH⊥EF交DF于H,
∵∠FEH=∠DEC=90°,
∴∠DEH=∠CEF,
∵∠EDH=∠ECF,DE=CE,
∴△DEH≌△CEF(ASA),
∴EF=EH,DH=CF,
∴AC﹣CF=DG﹣DH,
即AF=HG,
∵FH=FG+GH=EF,
∴AF+FG=EF.
30.解:(1)如图1,连接BD,DE,∵ABCD是平行四边形
∴AB∥CD,AB=CD
∴∠BCD=180°﹣∠ABC=180°﹣120°=60°
∵BC=2AB,点E是BC的中点
∴BE=CE=CD
∴△CDE是等边三角形
∴DE=CE=BE,∠CDE=∠CED=60°
∴∠CBD=∠BDE=30°
∴∠BDC=90°
∵CD=AB=5,
∴BC=10,BD===5
∴BP===2;
(2)如图2,连接BF,DE,由(1)知△CDE是等边三角形
∴DE=CE,∠CED=60°
∵BE=BF=BA,∠ABC=120°
∴∠AFB=(180°﹣∠ABF),∠BFE=(180°﹣∠EBF),
∴∠AFE=∠AFB+∠BFE=(180°﹣∠ABF)+(180°﹣∠EBF)=120°,
∴∠EFG=60°
∵GF=GE
∴△EFG是等边三角形
∴∠FEG=∠CED=60°,EF=EG
∴∠FEG﹣∠DEG=∠CED﹣∠DEG,即∠DEF=∠CEG
∴△DEF≌△CEG(SAS)
∴CG=DF.
一.选择题
1.如图,在?ABCD中,AE⊥BC,垂足为E,AF⊥CD,垂足为F.若AE:AF=2:3,?ABCD的周长为10,则AB的长为( )
A.2 B.2.5 C.3 D.3.5
2.如图,在平行四边形ABCD中,,AD=4,AC⊥BC,则△DBC比△ABC的周长长( )
A.2 B.4 C.5 D.
3.如图,在平行四边形ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB的长是( )
A.4 B.2 C.2 D.2
4.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB?AC;③OB=AB;④OE=BC.其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,在平行四边形ABCD中,点A、B、C的坐标分别为(2,0)、(0,1)、(1,2),则平行四边形ABCD的周长为( )
A. B.6 C.8 D.10
6.如图,在△ABC中,∠ACB=60°,∠CAB=45°,BC=4,点D为AB边上一个动点,连接CD,以DA、DC为一组邻边作平行四边形ADCE,则对角线DE的最小值是( )
A.+ B.1+ C.4 D.2+2
7.如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE,CF和EF,则下列结论,一定成立的个数是( )
①△CDF≌△EBC;②△CEF是等边三角形;③∠CDF=∠EAF;④CE∥DF
A.1 B.2 C.3 D.4
8.在平行四边形ABCD中,AB≠BC,F是BC上一点,AE平分∠FAD,且E是CD的中点,则下列结论:①AE⊥EF,②AF=CF+CD,③AF=CF+AD,④AB=BF,其中正确的是( )
A.②④ B.①② C.①③ D.①②④
9.如图,在平行四边形ABCD中,点E是BC的中点,作EF⊥AE交CD于F,若∠BAE=45°,AE=4,下列结论:①∠EAF=45°,②AF=AB+CF,③CD=2CF,④S△AEF=8中正确的是( )
A.①②④ B.①③④ C.①②③ D.②③④
10.如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边三角形△ACD和△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④其中,正确的是( )
A.只有①② B.只有①②③ C.只有③④ D.①②③④
二.填空题
11.已知平面直角坐标系上有三个点,点A(2,0),B(5,2),C(3,4),以点A,点B,点C为顶点画平行四边形,则第四个顶点D的坐标为_ .
12.如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是 .
13.在?ABCD中,对角线AC与BD相交于点O,在AB上有一点E,连接CE,过点B作BC的垂线和CE的延长线交于点F,连接AF,∠ABF=∠FCB,FC=AB.若FB=1,AF=,则BD= .
14.如图:在Rt△ABC中,AB=3,BC=4,∠B=90°,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是 .
15.如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=,AC=2,BD=4,则AE的长为 .
16.如图,在平行四边形ABCD中,AB=8,BC=12,∠B=120°,E是BC的中点,点P在平行四边形ABCD的边上,若△PBE为等腰三角形,则EP的长为 .
17.在平面直角坐标系中,已知三点O(0,0),A(1,﹣2),B(3,1),若以A、B、C、O为顶点的四边形是平行四边形,则点C的坐标为 .
18.如图,在直角坐标系中,?ABCO的顶点B的坐标为(6,m),C的坐标为(2,n)则点A的坐标为 .(用字母m,n表示)
19.如图,已知平行四边形ABCD,DE⊥CD,CE⊥BC,CE=AD,F为BC上一点,连接DF,且点A在BF的垂直平分线上,若DE=1,DF=5,则AD的长为 .
20.如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF= .
三.解答题
21.如图,?ABCD中,CG⊥AB于点G,∠ABF=45°,F在CD上,BF交CG于点E,连接AE,AE⊥AD.
(1)若BG=1,BC=,求EF的长度;
(2)求证:AB﹣BE=CF.
22.如图,在平行四边形ABCD中,E为AD上一点,连接EB并延长到点F,使BF=BE,连接EC并延长到点M,使CM=EC,连接FM,N为FM的中点,连接AF、DN
(1)求证:四边形AFND为平行四边形;
(2)在不添加任何辅助线的情况下,直接写出图中长度为FM的一半的所有线段.
23.如图,在平行四边形ABCD中,点E是AB边上一点,CE=AB,DF⊥BC,垂足为点F,交CE于点G,连接DE,EF.
(1)求证:∠AED=90°﹣∠DCE;
(2)若点E是AB边的中点,求证:∠EFB=∠DEF.
24.若平面内两点P1(x1,y2),P2(x2,y2),其两点间的距离P1P2=.例如:已知A(3,1),B(5,2),则这两点间的距离AB=.已知A(3,1),B(5,2),C(4,4).
(1)聪明的你能判定△ABC的形状吗?并说明理由.
(2)若以点A、B、C、D为顶点的四边形是平行四边形时,请直接写出点D的坐标.
25.如图,在四边形ABCD中,AD∥BC,AD=BC=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF.
(1)若∠ADC=80°,求∠ECF;
(2)求证:∠ECF=∠CEF.
26.已知:平行四边形ABCD中,∠ABC=45°,对角线AC⊥CD.
(1)如图1,若AD=6,求平行四边形ABCD的面积.
(2)如图2,连接BD交AC于O点,过点A作AE⊥BD于E,连接EC.求证:ED=AE+EC.
27.已知,在平行四边形ABCD中,DE⊥BC于E,点F是DE上一点,满足BA⊥BF,连接CF.
(1)如图1,连接AF,若BF=2,DC=4,∠DAF=30°,求AD;
(2)如图2,延长CF,交AD于点G,若BA=BF,求证:AG=2EF.
28.已知:平行四边形ABCD中,BD=CD,且∠ABD=45°,过D作DF⊥AB于F,点E是AD的中点,连接BE交DF于点P,点G是AB的中点,过B作BH⊥BD交PG的延长线于H.
(1)若AB=2,求DP的长;
(2)求证:DP=BH.
29.如图,在?ABCD中,∠B=45°,过点C作CE⊥AD于点,连接AC,过点D作DF⊥AC于点F,交CE于点G,连接EF.
(1)若DG=8,求对角线AC的长;
(2)求证:AF+FG=EF.
30.如图,已知平行四边形ABCD中,BC=2AB,点E是BC的中点,∠ABC=120°,点P为CD边上任意一点,连接BP,点G为BP上一点,连接AG,EG,CG,使∠AGB=∠EGB,点F在AG上,且GF=GE,连接EF,DF
(1)若AB=5,DP=3,求线段BP的长度;
(2)求证:CG=DF.
2020年人教版八下数学《18.1 平行四边形》专项提升【1】
参考答案与试题解析
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴BC+CD=10÷2=5,
根据平行四边形的面积公式,得BC:CD=AF:AE=3:2.
∴BC=3,CD=2,
∴AB=CD=2,
故选:A.
2.解:在?ABCD中,∵AB=CD=2cm,AD=BC=4cm,AO=CO,BO=DO,
∵AC⊥BC,
∴AC==6cm,
∴OC=3cm,
∴BO==5cm,
∴BD=10cm,
∴△DBC的周长﹣△ABC的周长=BC+CD+BD﹣(AB+BC+AC)=BD﹣AC=10﹣6=4cm,
故选:B.
3.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴CE=2AB,
∵∠BCD=∠BAD=120°,
∴∠ECF=60°,
∵EF⊥BC,
∴∠CEF=30°,
∴CE=2CF=4,
∴AB=2.
故选:B.
4.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
∴AE=BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S?ABCD=AB?AC,故②正确,
∵AB=BC,OB=BD,
∵BD>BC,
∴AB≠OB,故③错误;
或∵AC⊥AB,
∴AB<OB,故③错误;
∵∠CAD=30°,∠AEB=60°,AD∥BC,
∴∠EAC=∠ACE=30°,
∴AE=CE,
∴BE=CE,
∵OA=OC,
∴OE=AB=BC,故④正确.
故选:C.
5.解:∵点A、B的坐标分别为(2,0)、(0,1),
∴OA=2,OB=1,
∴AB==,
过C作CE⊥y轴于E,如图所示:
∵点C的坐标为(1,2),
∴CE=1,OE=2,
∴BE=1,
∴BC==,
∴AB+BC=+,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴平行四边形ABCD的周长=2(AB+BC)=2+2
故选:A.
6.解:设DE交AC于O,作BF⊥AC于F,如图所示:
则∠BFC=∠BFA=90°,
∵∠ACB=60°,∠CAB=45°,
∴∠CBF=30°,∠ABF=90°﹣45°=45°=∠CAB,
∴CF=BC=2,AF=BF=CF=2,
∴AC=CF+AF=2+2,
∵四边形ADCE是平行四边形,
∴AO=CO=AC=1+,DO=EO,
∴当OD⊥AB时,DO的值最小,即DE的值最小,
则△AOD是等腰直角三角形,
∴OD=AO=,
∴DE=2OD=+;
故选:A.
7.解:在?ABCD中,∠ADC=∠ABC,AD=BC,CD=AB,
∵△ABE、△ADF都是等边三角形,
∴AD=DF,AB=EB,∠DFA=∠ADF=∠ABE=60°,
∴DF=BC,CD=BE,
∴∠CDF=∠ADC﹣60°,
∠EBC=∠ABC﹣60°,
∴∠CDF=∠EBC,
在△CDF和△EBC中,,
∴△CDF≌△EBC(SAS),故①正确;
在?ABCD中,设AE交CD于O,AE交DF于K,如图:
∵AB∥CD,
∴∠DOA=∠OAB=60°,
∴∠DOA=∠DFO,
∵∠OKD=∠AKF,
∴∠ODF=∠OAF,
故③正确;
在△CDF和△EAF中,,
∴△CDF≌△EAF(SAS),
∴EF=CF,
∵△CDF≌△EBC,
∴CE=CF,
∴EC=CF=EF,
∴△ECF是等边三角形,故②正确;
则∠CFE=60°,
若CE∥DF时,
则∠DFE=∠CEF=60°,
∵∠DFA=60°=∠CFE,
∴∠CFE+∠DFE+∠DFA=180°,
则C、F、A三点共线
已知中没有给出C、F、A三点共线,故④错误;
综上所述,正确的结论有①②③.
故选:C.
8.解:延长AD,交FE的延长线于点M,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠M=∠EFC,
∵E是CD的中点,
∴DE=CE,
在△DEM和△CEF中,
,
∴△DEM≌△CEF(AAS),
∴EM=EF,
过点E作ET⊥AM于T,ER⊥AF于R.
∵AE平分∠FAD,
∴ET=ER,
∵EM=EF,∠ETM=∠ERF=90°,
∴Rt△ETM≌Rt△ERF(HL),
∴∠M=∠AFM,
∴AM=AF,
即AF=AD+DM=CF+AD;故③,①正确,②错误.
∵AF不一定是∠BAD的角平分线,
∴AB不一定等于BF,故④错误.
故选:C.
9.解:作EM∥AB交AF于M,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴AB∥EM∥CD,
∴AM:FM=BE:CE,∠AEM=∠BAE=45°,
∵点E是BC的中点,
∴BE=CE,
∴AM=FM,
∴EM是梯形ABCF的中位线,
∴AB+CF=2EM,
∵EF⊥AE,
∴∠AEF=90°,
∴EM=AF=AM=FM,
∴∠EAF=∠AEM=45°,AF=AB+CF,①②正确;
∴△AEF是等腰直角三角形,
∴FE=AE=4,
∴S△AEF═AE×FE=×4×4=8,④正确;
∵∠BAF=∠BAE+∠EAF=90°,
∴AF⊥AB,
∵AB∥CD,
∴AF⊥CD,
当AD=AC时,CF=DF,则CD=2CF,③不正确;
故选:A.
10.解:∵∠ACB=90°,∠ABC=30°,
∴∠BAC=60°,AC=AB,
∵△ACD是等边三角形,
∴∠ACD=60°,
∴∠ACD=∠BAC,
∴CD∥AB,
∵F为AB的中点,
∴BF=AB,
∴BF∥CD,CD=BF,
∴四边形BCDF为平行四边形,②正确;
∵四边形BCDF为平行四边形,
∴DF∥BC,又∠ACB=90°,
∴AC⊥DF,①正确;
∵DA=CA,DF=BC,AB=BE,BC+AC>AB
∴DA+DF>BE,③错误;
设AC=x,则AB=2x,
S△ACD=x2,S△ACB=x2,S△ABE=x2,
==,④错误,
故选:A.
二.填空题
11.解:以AC为对角线,将AB向上平移2个单位,再向左平移2个单位,A点对应的位置为(0,2)就是第四个顶点D;
以AB为对角线,将BC向下平移4个单位,再向左平移1个单位,B点对应的位置为(4,﹣2)就是第四个顶点D′;
以BC为对角线,将AB向上平移4个单位,再向右平移1个单位,B点对应的位置为(6,6)就是第四个顶点D″;
∴第四个顶点D的坐标为:(0,2)或(6,6)或(4,﹣2),
故答案为:(0,2)或(6,6)或(4,﹣2).
12.解:延长DC和AM交于E,过点E作EH⊥AN于点H,如图.
∵四边形ABCD为平行四边形,
∴AB∥CE,
∴∠BAM=∠CEM,∠B=∠ECM.
∵M为BC的中点,
∴BM=CM.
在△ABM和△ECM中,
,
∴△ABM≌△ECM(AAS),
∴AB=CD=CE,AM=EM=4,
∵N为边DC的中点,
∴NE=3NC=AB,即AB=NE,
∵AN=3,AE=2AM=8,且∠MAN=60°,
∴∠AEH=30°,
∴AH=AE=4,
∴EH==4,
∴NH=AH﹣AN=4﹣3=1,
∴EN==7,
∴AB=×7=.
故答案为.
13.解:延长BF、DA交于点G,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠GAB=∠ABC,
∵BF⊥BC,
∴∠FBC=∠FBA+∠ABC=90°,
∴∠FBA+∠GAB=90°,
∴∠G=90°,
在△AGB和△FBC中,
∵,
∴△AGB≌△FBC(AAS),
∴AG=BF=1,BC=BG,
Rt△AGF中,∵AF=,
∴FG=,
∴BC=BG=AD=3+1=4,
∴GD=1+4=5,
Rt△DGB中,BD=,
故答案为:.
14.解:∵在Rt△ABC中,∠B=90°,
∴BC⊥AB.
∵四边形ADCE是平行四边形,
∴OD=OE,OA=OC.
∴当OD取最小值时,DE线段最短,此时OD⊥BC.
∴OD∥AB,
∴OD是△ABC的中位线,
∴OD=AB=1.5,
∴ED=2OD=3.
故答案为:3.
15.解:∵AC=2,BD=4,四边形ABCD是平行四边形,
∴AO=AC=1,BO=BD=2,
∵AB=,
∴AB2+AO2=BO2,
∴∠BAC=90°,
∵在Rt△BAC中,BC=,
S△BAC=×AB×AC=×BC×AE,
∴2=AE,
∴AE=,
故答案为:.
16.解:当P点在BA上,BP=BE=6,
作BH⊥PE于H,如图1,则PH=EH,
∵∠B=120°,
∴∠BPE=∠BEP=30°,
在Rt△BEH中,BH=BE=3,EH=BH=3,
∴PE=2EH=6;
当P点在AD上,BP=PE,
作BG⊥AD于G,PF⊥BE于F,如图2,则BF=EF=3,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∵∠ABC=120°,
∴∠A=60°,
在Rt△ABG中,AG=AB=4,BG=AG=4,
∴PF=4,
在Rt△PEF中,PE==;
当点P在CD上,如图3,EB=EP=6,
综上所述,PE的长为6或6或.
故答案为6或6或.
17.解:如图,观察图象可知,满足条件的点C的坐标为(2,3)或(﹣2,﹣3)或(4,﹣1)
故答案为(2,3)或(﹣2,﹣3)或(4,﹣1).
18.解:∵?ABCO的顶点B的坐标为(6,m),C的坐标为(2,n),OA∥BC,OA=BC,
∴B、C横坐标的差为6﹣2=4,纵坐标的差为m﹣n,
∵O(0,0),
∴则点A的坐标为(4,m﹣n);
故答案为:(4,m﹣n).
19.解:连接AF,AC,过点A作AH⊥CD于H,AH交EC于O,
设AD与CE交于G,
∵∠AGC=∠AHC=90°,∠AOG=∠COH,
∴∠DAH=∠ECD,
∵∠AHD=∠EDC=90°,AD=CE,
∴△ADH≌△CED(AAS),
∴DE=DH=1,AH=CD,
∵点A在BF的垂直平分线上,
∴AB=AF,
∴∠ABF=∠AFB,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∴∠ABF+∠BCD=180°,
∴∠BCD=∠AFC,
∵CF=CF,
∴△AFC≌△DCF(SAS),
∴DF=AC=5,
设CH=x,则AH=CD=x+1,
∵AH2+CH2=AC2,
∴(x+1)2+x2=52,
解得:x=3(负值舍去),
∴AH=4,
∴AD==,
故答案为:.
20.解:如图,延长AE,BC交于点G,
∵点E是CD的中点,
∴DE=CE,
∵平行四边形ABCD中,AD∥BC,
∴∠D=∠ECG,
又∵∠AED=∠GEC,
∴△ADE≌△GCE,
∴CG=AD=5,AE=GE,
又∵AE平分∠FAD,AD∥BC,
∴∠FAE=∠DAE=∠G=∠DAF=30°,
∴AF=GF=3+5=8,
又∵E是AG的中点,
∴FE⊥AG,
∴Rt△AEF中,EF=AF=4,
故答案为:4.
三.解答题
21.解:(1)∵CG⊥AB,BG=1,,
∴.
∵∠ABF=45°,
∴△BGE是等腰直角三角形,
∴EG=BG=1,
∴EC=CG﹣EG=3﹣1=2,
∵在平行四边形ABCD中,AB∥CD,∠ABF=45°,CG⊥AB,
∴∠CFE=∠ABF=45°,∠FCE=∠BGE=90°,
∴△ECF是等腰直角三角形,
∴EF==2;
(2)证明:过E作EH⊥BE交AB于H,
∵∠ABF=45°,∠BEH=90°,
∴△BEH是等腰直角三角形,
∴,BE=HE,
∴∠BHE=45°,
∴∠AHE=180°﹣∠BHE=180°﹣45°=135°,
由(1)知,△BGE和△ECF都是等腰直角三角形,
∴∠BEG=45°,CE=CF,
∴∠BEC=180°﹣∠BEG=180°﹣45°=135°,
∴∠AHE=∠CEB,
∵AE⊥AD,
∴∠DAE=90°,
∴∠BAD=∠DAE+∠EAB=90°+∠EAB,
由(1)知,∠FCE=90°,
∴∠BCD=∠FCE+∠BCG=90°+∠BCG,
∵在平行四边形ABCD中,∠BAD=∠BCD,
∴90°+∠EAB=90°+∠BCG,
∴∠EAB=∠BCG,
即∠EAH=∠BCE,
在△△EAH和△BCE中,
∴△EAH≌△BCE(AAS),
∴AH=CE=CF,
∴AB﹣BE=AB﹣BH=AH=CF,
即AB﹣BE=CF.
22.(1)证明:如图,∵EB=BF,EC=CM,
∴BC∥FM,BC=FM,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD∥FM,
∵N为FM的中点,
∴FN=FM,
∴AD=FN,
∴四边形AFND是平行四边形;
(2)解:∵四边形ABCD为平行四边形,
∴AD=BC,
∵BF=BE,CM=CE,
∴BC=FM,
∴AD=FM,
∵四边形AFND是平行四边形,
∴FN=AD=FM,
∴MN=FM,
∴长度为FH的一半的所有线段为:AD,BC,FN,MN.
23.证明:(1)∵CE=AB,AB=CD
∴CE=CD,
∴∠CDE=∠CED==90°﹣∠DCE,
∵CD∥AB
∴∠AED=∠CDE=90°﹣∠DCE;
(2)如图,延长DA,FE于点M,
∵四边形ABCD是平行四边形
∴AD∥BC,且DF⊥BC
∴DF⊥AD,∠M=∠EFB
∵∠M=∠EFB,AE=BE,∠AEM=∠FEB
∴△AEM≌△BEF(AAS)
∴ME=EF,且DF⊥DM
∴ME=DE=EF
∴∠M=∠MDE
∴∠DEF=∠M+∠MDE=2∠M
∴∠EFB=∠DEF
24.解:(1)能判定△ABC的形状,△ABC是等腰直角三角形;理由如下:
由题意得:AB=,BC==,AC==,
∴AB=BC,AB2+BC2=AC2,
∴△ABC是等腰直角三角形;
(2)如图所示:
当AB为对角线时,AD∥BC,
∵A(3,1),B(5,2),C(4,4),
∴把点B向下平移3个单位,再向左平移1个单位,得到点D,
∴点D的坐标为(4,﹣1);
当BC为对角线时,AB∥CD,
∵A(3,1),B(5,2),C(4,4),
∴把点B向上平移3个单位,再向右平移1个单位,得到点D',
∴点D'的坐标为(6,5);
当AC为对角线时,AD∥BC,
∵A(3,1),B(5,2),C(4,4),
∴把点A向上平移2个单位,再向左平移1个单位,得到点D'',
∴点D''的坐标为(2,3);
综上所述,点D的坐标为(4,﹣1)或(6,5)或(2,3).
25.解:(1)∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵F是AD的中点,
∴AF=FD,
∵在?ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF=(180°﹣80°)=50°,
∵CE⊥AB,
∴CE⊥CD,
∴∠DCE=90°,
∴∠ECF=90°﹣50°=40°;
(2)如图,延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=EM=FE,
∴∠ECF=∠CEF.
26.解:解法一:(1)∵∠ABC=45°,AC⊥CD,
∴△ACD是等腰直角三角形,
∵AD=6,
∴AC=CD=AD=3,
∴平行四边形ABCD的面积=33=18;
(2)过C作FC⊥EC交BD于F,
∵AE⊥BD,
∴∠AEO=∠CFO=90°,
∵∠AOE=∠COF,
∵平行四边形ABCD中,AO=CO,
∴△AOE≌△COF(AAS),
∴AE=CF,OE=OF,
∵∠ABC=45°,AC⊥CD,
∴△ACD是等腰直角三角形,
设AC=AB=2x,
∴AD=BC=2x,
∴AO=x,
∴BO=DO==x,
∵S△AOB=AB?AO=BO?AE,
∴AE===,
∴OE=OF==x,
∴EF=CF=x,
∴CE=EF=x,
∵DE==x,AE+EC=x+x=x,
∴ED=AE+EC;
解法二:过C作FC⊥EC交BD于F,∴∠FCE=90°,
∵AE⊥BD,
∴∠ACD=90°,
∴∠ECA+∠ACF=∠ACF+∠FCD,
∴∠ECA=∠FCD,
∵AE⊥BD,
∴∠AEB=90°,
∴∠ABD+∠BAE=∠BAE+∠EAC,
∴∠EAC=∠CDF,
∵AC⊥CD,∠ADC=∠ABC=45°,
∴△ACD是等腰直角三角形,
∴AC=CD,
∴△AEC≌△DFC(ASA),
∴AE=DF,EC=FC,
∴△ECF是等腰直角三角形,
∴EF=EC,
∴ED=DF+EF=AE+EC.
27.解:(1)∵四边形ABCD是平行四边形,
∴AB=CD=4,
∵BA⊥BF,
∴∠ABF=90°,
∵BF=2,
∴AF===10,
∵AD∥BC,DE⊥BC,
∴DE⊥AD,
∴∠ADF=90°,
∵∠DAF=30°,
∴AD=AF=5;
(2)∵在平行四边形ABCD中,AB=CD,AD∥BC,∠A=∠BCD,
又∵BA=BF,
∴BF=CD,∠A+∠ABC=180°,
∵BA⊥BF,
∴∠ABF=90°,
∴∠A+∠EBF=90°,
∵∠EDC+∠DCE=90°,
∴∠EBF=∠EDC,
∵DE⊥BC,
∴∠BEF=∠DEC=90°,
∴△BEF≌△DEC(AAS),
∴EF=CE,BE=DE,
∴∠EFC=∠ECF=45°,
∵∠DFG=∠CFE=45°,
∴△DFG是等腰直角三角形,
∴DG=DF,
设DG=DF=x,EF=CE=y,
∴BE=DE=x+y,
∴AD=BC=x+y+y=x+2y,
∴AG=AD﹣DG=x+2y﹣x=2y=2EF.
28.(1)解:如图,过P作PM⊥BD于M,
∵四边形ABCD是平行四边形,
∴CD=AB=2,
∵BD=CD,
∴AB=BD=2,
∵E是AD的中点,
∴∠DBE=∠ABE,
∵PF⊥AB,PM⊥BD,
∴PF=PM,
∵∠ABD=45°,
∴△BDF是等腰直角三角形,
∴DF=BF=,∠BDF=45°,
∴DM=PM,PD=DM,
在△BFP和△BMP中,
∵,
∴Rt△BFP≌Rt△BMP(HL),
∴BM=BF=,
∴DM=2﹣,
∴DP=DM=2﹣2;
(2)证明:连接AP,
∵∠DEP=∠PFB=90°,∠EPD=∠FPB,
∴∠EDP=∠FBP,
在△ADF和△PBF中,
∵,
∴△ADF≌△PBF(ASA),
∴PF=AF,
∴∠PAF=45°,
∵BD⊥BH,
∴∠DBH=90°,
∵∠DBF=45°,
∴∠HBG=90°﹣45°=45°,
∴∠PAF=∠HBG,
在△APG和△BHG中,
∵,
∴△APG≌△BHG(ASA),
∴BH=AP,
∵AB=BD,∠ABD=45°,
∴∠DAB=∠ADB=67.5°,
Rt△ADF中,∠ADP=∠DAP=22.5°,
∴AP=DP,
∴DP=BH.
29.解:(1)∵在?ABCD中,∠B=45°,
∴∠ADC=∠B=45°,
∵CE⊥AD,
∴△CDE是等腰直角三角形,
∴CE=DE,∠DEC=∠AEC=90°,
∵DF⊥AC,
∴∠CFD=∠DEC=90°,
∴∠DGE=∠CGF,
∴∠EDG=∠ECA,
∴△DEG≌△CEA(ASA),
∴AC=DG=8;
(2)过E作EH⊥EF交DF于H,
∵∠FEH=∠DEC=90°,
∴∠DEH=∠CEF,
∵∠EDH=∠ECF,DE=CE,
∴△DEH≌△CEF(ASA),
∴EF=EH,DH=CF,
∴AC﹣CF=DG﹣DH,
即AF=HG,
∵FH=FG+GH=EF,
∴AF+FG=EF.
30.解:(1)如图1,连接BD,DE,∵ABCD是平行四边形
∴AB∥CD,AB=CD
∴∠BCD=180°﹣∠ABC=180°﹣120°=60°
∵BC=2AB,点E是BC的中点
∴BE=CE=CD
∴△CDE是等边三角形
∴DE=CE=BE,∠CDE=∠CED=60°
∴∠CBD=∠BDE=30°
∴∠BDC=90°
∵CD=AB=5,
∴BC=10,BD===5
∴BP===2;
(2)如图2,连接BF,DE,由(1)知△CDE是等边三角形
∴DE=CE,∠CED=60°
∵BE=BF=BA,∠ABC=120°
∴∠AFB=(180°﹣∠ABF),∠BFE=(180°﹣∠EBF),
∴∠AFE=∠AFB+∠BFE=(180°﹣∠ABF)+(180°﹣∠EBF)=120°,
∴∠EFG=60°
∵GF=GE
∴△EFG是等边三角形
∴∠FEG=∠CED=60°,EF=EG
∴∠FEG﹣∠DEG=∠CED﹣∠DEG,即∠DEF=∠CEG
∴△DEF≌△CEG(SAS)
∴CG=DF.
