8.3 简单几何体的表面积与体积(1)课件(共19张PPT)
文档属性
| 名称 | 8.3 简单几何体的表面积与体积(1)课件(共19张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 14:24:34 | ||
图片预览





文档简介
第8章 立体几何初步
8.3 简单几何体
的表面积与体积(1)
高中数学人教A版(2019)必修 第二册
棱柱、棱锥、棱台的表面积
小学我们就学过,正方体、长方体的表面积就是各个面的面积之和
正方体、长方体的表面积
长宽高分别为 ????,????,?????的长方体的表面积
?
棱长为 ???? 的正方体的表面积
?
????长方体=????????????+????????+????????
?
????正方体=????????????
?
????
?
????
?
????
?
求多面体的表面积体现了立体几何问题平面化的转化思想
探究新知
棱柱、棱锥、棱台的表面积
正方体、长方体的表面积
一个长方体的表面积是20cm3,所有棱长的和是24cm,求长方体的体对角线长度.
设长方体的长宽高分别为 ?????????????,?????????????,?????????????,体对角线长为 ?????????????,由题意有:
?
2????????+????????+????????=20,①4????+????+????=24,??②
?
,②式两边平方,得:
????2+????2+????2+2????????+2????????+2????????=36 ③
?
③?①,得 ????2+????2+????2=16,所以????=????????????
?
即体对角线长为4cm
????
?
例题讲解
棱柱、棱锥、棱台的表面积
★ 棱柱的侧面展开图是平行四边形,一边为棱柱的侧棱,
另一边等于棱柱的底面周长;
★ 棱锥的侧面展开图由若干个三角形组成;
★ 棱台的侧面展开图由若干个梯形组成.
棱柱、棱锥、棱台的侧面展开图
????棱柱=????侧+????????底
?
????棱锥=????侧+????底
?
????棱台=????侧+????上底+????下底
?
探究新知
圆柱、圆锥、圆台的表面积
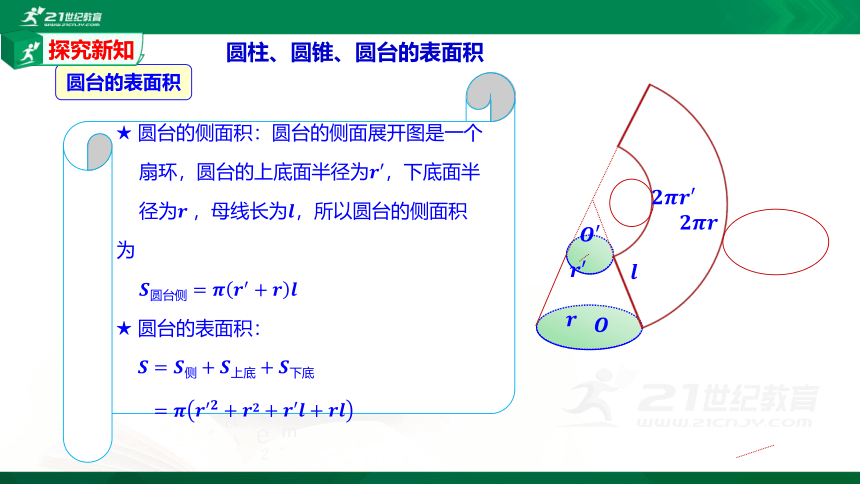
★ 圆柱的侧面积:圆柱的侧面展开图是一个矩形,圆柱的底面半径为????,
母线长为?????,那么这个矩形的一边长就是圆柱的底面周长,另一边的
长就是圆柱的母线长,所以圆柱的侧面积为 ????圆柱侧=????????????????
★ 圆柱的表面积:????=????????侧+????????底=????????????????+????????????????=????????????(????+????)
?
圆柱的表面积
探究新知
圆柱、圆锥、圆台的表面积
★ 圆锥的侧面积:圆锥的侧面展开图是一个扇形,
圆锥的底面半径为?????,母线长为?????,那么这个扇形
的弧长为圆锥的底面周长,半径为圆锥的母线
长,所以圆锥的侧面积为????圆锥侧=????????????
★ 圆锥的表面积:
????=????侧+????底= ????????????+????????????=????????(????+????)
?
圆锥的表面积
????
?
????
?
????
?
????????????
?
探究新知
圆柱、圆锥、圆台的表面积
★ 圆台的侧面积:圆台的侧面展开图是一个
扇环,圆台的上底面半径为????′,下底面半
径为?????,母线长为????,所以圆台的侧面积为
????圆台侧=????????′+????????
★ 圆台的表面积:
????=????侧+????上底+????下底
= ????????′????+????????+????′????+????????
?
圆台的表面积
????????????
?
????????????′
?
????′
?
????′
?
????
?
????
?
????
?
探究新知
柱体、椎体、台体的体积
★ 柱体(棱柱、圆柱)的高:柱体的两底面之间的距离,即从一底面上任意
一点,向另一底面作垂线,这点与垂足(垂线与底面之间的交点)之间的
距离,也就是垂线段的长.
★柱体(棱柱、圆柱)的体积:柱体的体积 ????柱体 等于它的底面积 ????底 和高 ????
的乘积,即 ????柱体=????底????
?
柱体(棱柱、圆柱)的体积
????底
?
????底
?
????底
?
????
?
????
?
????
?
探究新知
★ 椎体(棱锥、圆锥)的高:椎体的顶点到底面之间的距离,即从顶点向底
面作垂线,顶点与垂足(垂线与底面之间的交点)之间的距离,即垂线段
的长.
★椎体(棱锥、圆锥)的体积:椎体的体积 ????锥 等于它的底面积 ????底 和高 ????
乘积的 13,即 ????锥=13????底????
?
????
?
????
?
柱体、椎体、台体的体积
锥体(棱锥、圆锥)的体积
探究新知
——棱柱与棱锥体积之间的关系
一个三棱柱可以分解成三个体积相等的三棱锥,如图所示:
????
?
????
?
????
?
????????
?
????????
?
????????
?
????
?
????
?
????
?
????????
?
????????
?
????
?
????
?
????????
?
????????
?
????????
?
????????
?
????
?
【结论】棱锥的体积等于同底等高的棱柱体积的 13 ;
【同理】圆锥的体积等于同底等高的圆柱体积的 13 .
?
柱体、椎体、台体的体积
锥体(棱锥、圆锥)的体积
探究新知
柱体、椎体、台体的体积
台体(棱台、圆台)的体积
★ 台体(棱台、圆台)的高:台体的两底面之间的距离,即从上底面任意一点
向下底面作垂线,此点与垂足(垂线与底面之间的交点)之间的距离,即垂
线段的长.
★台体(棱台、圆台)的体积:????台体=13(????′+????′????+????)?????
(????′,????分别为上下底面的面积, ???? 为台体的高)
?
探究新知
柱体、椎体、台体的体积
柱体、椎体、台体体积之间的关系
从柱体、锥体、台体的形状可以看出,当台体上底面缩为一点时,台体成为椎体;当台体上底面放大到与下底面相同时,台体成为柱体.因此只要分别令 和 ,便可以从台体的体积公式得到柱体和椎体的体积公式.从而椎体和椎体的体积公式可以统一为台体的体积公式.
????台体=13(????′+????′????+????)????
?
????柱体=????????
?
????柱体=13????????
?
????′=????
?
????′=????
?
探究新知
球的体积和表面积
★ 球的体积公式:????=???????????????????? (其中R为球的半径)
★ 球的表面积公式:????=???????????????? (其中R为球的半径)
?
????
?
????
?
????
?
????
?
(1)从公式看,球的体积和表面积的大小,只与球的半径有关,
给定一个半径R都有唯一确定的V和S与之对应,所以球的
体积和表面积都是半径R的函数;
——球的体积与表面积公式的几点认识
(2)球的表面积恰好是是球的大圆(通过球心的平面截球所得的
圆)面积的4倍.
探究新知
求几何体体积的常用方法
常见多面体的体积公式
①正方体(棱长为????):
?
②长方体(长宽高为????,????,????):
?
????=????????
?
????=????????????
?
③正四面体(棱长为????):
?
????=????????????????????
?
常见旋转体的体积公式
①圆柱(底面半径为????,母线长为????):
?
????=????????????????
?
②圆锥(底面半径????,高为????):
?
????=????????????????????????
?
③圆台(上下底面半径为????????,????????,高为????):
?
????=????????????(????????????+????????????????+????????????)????
?
——公式法
归纳小结
[北京大兴区2020高一期末]三棱锥的三条侧棱两两垂直,长度分别为1,2,3,则这个三棱锥的体积为多少?
如右图所示,设PA=1,PB=2,PC=3,
且PA,PB,PC相互垂直
????
?
????
?
????
?
????
?
所以
?????????????????????=????????·????????·????????????????????=????????×????×????????×????×????=????
?
例题讲解
求几何体体积的常用方法
将原几何体补成易求解的几何体,如棱锥补成棱柱,三棱柱补成四棱柱等
——补形法
三棱锥A-BCD的高为4,底面BCD为直角三角形,两直角边BD和CD的长分别为5和3,求该三棱锥的体积.
如右图所示,把三棱锥放到长方体中,长方体的长宽高分别为5,3,4,ΔBCD为直角三角形,所以该三棱锥的体积
????
?
????
?
????
?
????
?
?????????????????????=????????×????????×????×????×????=????????
?
例题讲解
如图,在多面体ABCDEF中,已知四边形ABCD是边长为1的正方形,且ΔADE,ΔBCF均为正三角形,EF//AB,EF=2,求该多面体的体积.
求几何体体积的常用方法
将原几何体分割成容易求解体积的几个部分,分别求体积,再求和
——分割法
如图,分别过点A,B作EF的垂线,垂足分别为DG,CH,易知EG=HF= ?????????,AG=GD=BH=HC= ?????????,则ΔBHC中BC
边的高????=????????,
?
????
?
????
?
????
?
????
?
????=?????????????????????+?????????????????????+?????????????????????????????=?????????????????????????+?????????????????????
?
????
?
????
?
所以????????????????????=????????????????????=????????×????????×1=????????
?
所以该多面体的体积
=????×????????×????????×????????+????????×????=????????
?
????
?
????
?
例题讲解
谢谢聆听
8.3 简单几何体
的表面积与体积(1)
高中数学人教A版(2019)必修 第二册
棱柱、棱锥、棱台的表面积
小学我们就学过,正方体、长方体的表面积就是各个面的面积之和
正方体、长方体的表面积
长宽高分别为 ????,????,?????的长方体的表面积
?
棱长为 ???? 的正方体的表面积
?
????长方体=????????????+????????+????????
?
????正方体=????????????
?
????
?
????
?
????
?
求多面体的表面积体现了立体几何问题平面化的转化思想
探究新知
棱柱、棱锥、棱台的表面积
正方体、长方体的表面积
一个长方体的表面积是20cm3,所有棱长的和是24cm,求长方体的体对角线长度.
设长方体的长宽高分别为 ?????????????,?????????????,?????????????,体对角线长为 ?????????????,由题意有:
?
2????????+????????+????????=20,①4????+????+????=24,??②
?
,②式两边平方,得:
????2+????2+????2+2????????+2????????+2????????=36 ③
?
③?①,得 ????2+????2+????2=16,所以????=????????????
?
即体对角线长为4cm
????
?
例题讲解
棱柱、棱锥、棱台的表面积
★ 棱柱的侧面展开图是平行四边形,一边为棱柱的侧棱,
另一边等于棱柱的底面周长;
★ 棱锥的侧面展开图由若干个三角形组成;
★ 棱台的侧面展开图由若干个梯形组成.
棱柱、棱锥、棱台的侧面展开图
????棱柱=????侧+????????底
?
????棱锥=????侧+????底
?
????棱台=????侧+????上底+????下底
?
探究新知
圆柱、圆锥、圆台的表面积
★ 圆柱的侧面积:圆柱的侧面展开图是一个矩形,圆柱的底面半径为????,
母线长为?????,那么这个矩形的一边长就是圆柱的底面周长,另一边的
长就是圆柱的母线长,所以圆柱的侧面积为 ????圆柱侧=????????????????
★ 圆柱的表面积:????=????????侧+????????底=????????????????+????????????????=????????????(????+????)
?
圆柱的表面积
探究新知
圆柱、圆锥、圆台的表面积
★ 圆锥的侧面积:圆锥的侧面展开图是一个扇形,
圆锥的底面半径为?????,母线长为?????,那么这个扇形
的弧长为圆锥的底面周长,半径为圆锥的母线
长,所以圆锥的侧面积为????圆锥侧=????????????
★ 圆锥的表面积:
????=????侧+????底= ????????????+????????????=????????(????+????)
?
圆锥的表面积
????
?
????
?
????
?
????????????
?
探究新知
圆柱、圆锥、圆台的表面积
★ 圆台的侧面积:圆台的侧面展开图是一个
扇环,圆台的上底面半径为????′,下底面半
径为?????,母线长为????,所以圆台的侧面积为
????圆台侧=????????′+????????
★ 圆台的表面积:
????=????侧+????上底+????下底
= ????????′????+????????+????′????+????????
?
圆台的表面积
????????????
?
????????????′
?
????′
?
????′
?
????
?
????
?
????
?
探究新知
柱体、椎体、台体的体积
★ 柱体(棱柱、圆柱)的高:柱体的两底面之间的距离,即从一底面上任意
一点,向另一底面作垂线,这点与垂足(垂线与底面之间的交点)之间的
距离,也就是垂线段的长.
★柱体(棱柱、圆柱)的体积:柱体的体积 ????柱体 等于它的底面积 ????底 和高 ????
的乘积,即 ????柱体=????底????
?
柱体(棱柱、圆柱)的体积
????底
?
????底
?
????底
?
????
?
????
?
????
?
探究新知
★ 椎体(棱锥、圆锥)的高:椎体的顶点到底面之间的距离,即从顶点向底
面作垂线,顶点与垂足(垂线与底面之间的交点)之间的距离,即垂线段
的长.
★椎体(棱锥、圆锥)的体积:椎体的体积 ????锥 等于它的底面积 ????底 和高 ????
乘积的 13,即 ????锥=13????底????
?
????
?
????
?
柱体、椎体、台体的体积
锥体(棱锥、圆锥)的体积
探究新知
——棱柱与棱锥体积之间的关系
一个三棱柱可以分解成三个体积相等的三棱锥,如图所示:
????
?
????
?
????
?
????????
?
????????
?
????????
?
????
?
????
?
????
?
????????
?
????????
?
????
?
????
?
????????
?
????????
?
????????
?
????????
?
????
?
【结论】棱锥的体积等于同底等高的棱柱体积的 13 ;
【同理】圆锥的体积等于同底等高的圆柱体积的 13 .
?
柱体、椎体、台体的体积
锥体(棱锥、圆锥)的体积
探究新知
柱体、椎体、台体的体积
台体(棱台、圆台)的体积
★ 台体(棱台、圆台)的高:台体的两底面之间的距离,即从上底面任意一点
向下底面作垂线,此点与垂足(垂线与底面之间的交点)之间的距离,即垂
线段的长.
★台体(棱台、圆台)的体积:????台体=13(????′+????′????+????)?????
(????′,????分别为上下底面的面积, ???? 为台体的高)
?
探究新知
柱体、椎体、台体的体积
柱体、椎体、台体体积之间的关系
从柱体、锥体、台体的形状可以看出,当台体上底面缩为一点时,台体成为椎体;当台体上底面放大到与下底面相同时,台体成为柱体.因此只要分别令 和 ,便可以从台体的体积公式得到柱体和椎体的体积公式.从而椎体和椎体的体积公式可以统一为台体的体积公式.
????台体=13(????′+????′????+????)????
?
????柱体=????????
?
????柱体=13????????
?
????′=????
?
????′=????
?
探究新知
球的体积和表面积
★ 球的体积公式:????=???????????????????? (其中R为球的半径)
★ 球的表面积公式:????=???????????????? (其中R为球的半径)
?
????
?
????
?
????
?
????
?
(1)从公式看,球的体积和表面积的大小,只与球的半径有关,
给定一个半径R都有唯一确定的V和S与之对应,所以球的
体积和表面积都是半径R的函数;
——球的体积与表面积公式的几点认识
(2)球的表面积恰好是是球的大圆(通过球心的平面截球所得的
圆)面积的4倍.
探究新知
求几何体体积的常用方法
常见多面体的体积公式
①正方体(棱长为????):
?
②长方体(长宽高为????,????,????):
?
????=????????
?
????=????????????
?
③正四面体(棱长为????):
?
????=????????????????????
?
常见旋转体的体积公式
①圆柱(底面半径为????,母线长为????):
?
????=????????????????
?
②圆锥(底面半径????,高为????):
?
????=????????????????????????
?
③圆台(上下底面半径为????????,????????,高为????):
?
????=????????????(????????????+????????????????+????????????)????
?
——公式法
归纳小结
[北京大兴区2020高一期末]三棱锥的三条侧棱两两垂直,长度分别为1,2,3,则这个三棱锥的体积为多少?
如右图所示,设PA=1,PB=2,PC=3,
且PA,PB,PC相互垂直
????
?
????
?
????
?
????
?
所以
?????????????????????=????????·????????·????????????????????=????????×????×????????×????×????=????
?
例题讲解
求几何体体积的常用方法
将原几何体补成易求解的几何体,如棱锥补成棱柱,三棱柱补成四棱柱等
——补形法
三棱锥A-BCD的高为4,底面BCD为直角三角形,两直角边BD和CD的长分别为5和3,求该三棱锥的体积.
如右图所示,把三棱锥放到长方体中,长方体的长宽高分别为5,3,4,ΔBCD为直角三角形,所以该三棱锥的体积
????
?
????
?
????
?
????
?
?????????????????????=????????×????????×????×????×????=????????
?
例题讲解
如图,在多面体ABCDEF中,已知四边形ABCD是边长为1的正方形,且ΔADE,ΔBCF均为正三角形,EF//AB,EF=2,求该多面体的体积.
求几何体体积的常用方法
将原几何体分割成容易求解体积的几个部分,分别求体积,再求和
——分割法
如图,分别过点A,B作EF的垂线,垂足分别为DG,CH,易知EG=HF= ?????????,AG=GD=BH=HC= ?????????,则ΔBHC中BC
边的高????=????????,
?
????
?
????
?
????
?
????
?
????=?????????????????????+?????????????????????+?????????????????????????????=?????????????????????????+?????????????????????
?
????
?
????
?
所以????????????????????=????????????????????=????????×????????×1=????????
?
所以该多面体的体积
=????×????????×????????×????????+????????×????=????????
?
????
?
????
?
例题讲解
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
